基于Hiles and Mott渗流模型的有界储层产量递减模型

doi:10.11764/j.issn.1672-1926.2022.04.003

基于Hiles and Mott渗流模型的有界储层产量递减模型

詹泽东^,¹^,²^,³, 郭彤楼², 赵爽², 王勇飞², 郭科³, 周仲礼³, 毕有益²

1.成都理工大学地球物理学院，四川成都 610059

2.中国石油化工股份有限公司西南油气分公司，四川成都 610041

3.成都理工大学四川省数学地质重点实验室，四川成都 610059

Research and application of production decline model for bounded reservoir based on Hiles and Mott’s mechanism

ZHAN Zedong^,¹^,²^,³, GUO Tonglou², ZHAO Shuang², WANG Yongfei², GUO Ke³, ZHOU Zhongli³, BI Youyi²

1.College of Geophysics，Chengdu University of Technology，Chengdu 610059，China

2.Southwest Oil & Gas Company，SINOPEC，Chengdu 610041，China

3.Key Laboratory of Geomathematics of Sichuan Province，Chengdu University of Technology，Chengdu 610059，China

收稿日期: 2022-01-28 修回日期: 2022-03-26 网络出版日期: 2022-04-13

基金资助:

国家科技重大专项. 2016ZX05048004
中国石化科技项目. P20055-6

Received: 2022-01-28 Revised: 2022-03-26 Online: 2022-04-13

作者简介 About authors

詹泽东（1986-），男，四川内江人.高级工程师，硕士，主要从事油气开发研究及管理工作.E-mail：superzzdxnyq@sina.com. , E-mail：superzzdxnyq@sina.com

摘要

根据油气井实际生产过程中普遍存在近似先定产降压、再定压降产的生产特征，开展在有界储层拟稳态阶段改用定压生产模式的产量递减模型研究，为明确油气井产量递减的渗流机理提供一种新的理论依据。依托Hiles and Mott模型，通过理论推导建立了有界储层在拟稳态阶段定压生产的产量递减模型。结果表明：该模型形式上与Arps递减模型具有一致性，但相比Arps产量递减模型，该模型更具一般性，即当Hiles and Mott指数为1时，流体渗流遵循达西定律，拟稳态阶段改变生产方式为定压生产情况下，油气井产量递减遵行指数递减；当Hiles and Mott指数在0.5~1区间时，流体渗流表现为高速非达西渗流，递减模型为幂律递减；当Hiles and Mott指数为0.5时，遵行直线递减模型；当Hiles and Mott指数大于1时，流体渗流为非达西低速渗流条件下，产量递减模型转化为双曲递减模型，并且用Arps形式表征的3个参数之间具有非线性相关性，且满足质量守恒定律，特别是当Hiles and Mott指数趋于无限大时，油气井产量递减模型无限接近于Arps递减模型的调和递减。这就为有界储层采用Arps递减模型开展油气井动态诊断赋予了渗流机理解释，解释了Arps递减模型质量不守恒和调和递减累计产量模型无界性的原因，对深入与扩展Arps产量递减模型的应用具有重要理论意义，也为利用产量递减模型开展储层参数反演提供了科学依据。

关键词： 渗流机理 ; 拟稳态 ; 产量递减 ; Arps ; 质量守恒

Abstract

According to the common production characteristics in the actual production process of oil and gas wells， the production decline model under the change of constant pressure production mode to the quasi-steady state of bounded reservoir is studied， which provides a new theoretical basis for defining the seepage mechanism of oil and gas well production decline. Based on Hiles and Mott’s mechanism， through theoretical derivation， a new production decline model is established when the bounded reservoir reaches quasi-steady state in the late stage of boundary flow， under the condition of a constant pressure production. The results show that the model is formally consistent with Arps’ decline model， and its three decline parameters have exponential correlation. However， compared with Arps’ production decline model， this model is more extensive and general. That is， when the exponential coefficient from Hiles and Mott’s constitutive equation is 1， which means fluid seepage follows Darcy's law， the production decline of oil and gas wells follows exponential decline， with the condition of pseudo steady state， because of boundary effect. When the exponential coefficient from Hiles and Mott’s constitutive equation varies between 0 and 1， the fluid is in the transitional state of Darcy flow and turbulence， and the decline curve is a power function decline， and specially when the exponential coefficient from Hiles and Mott’s constitutive equation is 0.5， which means the fluid is in a turbulent state， and the production decline curve of oil and gas wells is a straight line. When the exponential coefficient is greater than 1， which means fluid seepage is low-speed non Darcy flow， the production decline becomes a hyperbolic decline curve， and the three characterization parameters of hyperbolic decline have nonlinear correlation， and the decline model satisfies the law of mass conservation. This not only lays a theoretical foundation for the analysis and discrimination of fluid seepage characteristics in the quasi steady state stage of bounded reservoir， but also provides a scientific basis for reservoir parameter inversion using production decline model， which is of great significance for deepening and expanding the application of Arps’ production decline model， so it has strong practicability and foresight.

Keywords： Seepage mechanism ; Quasi steady state ; Production decline ; Arps ; Mass conservation

PDF (1496KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

詹泽东, 郭彤楼, 赵爽, 王勇飞, 郭科, 周仲礼, 毕有益. 基于Hiles and Mott渗流模型的有界储层产量递减模型. 天然气地球科学[J], 2022, 33(9): 1509-1517 doi:10.11764/j.issn.1672-1926.2022.04.003

ZHAN Zedong, GUO Tonglou, ZHAO Shuang, WANG Yongfei, GUO Ke, ZHOU Zhongli, BI Youyi. Research and application of production decline model for bounded reservoir based on Hiles and Mott’s mechanism. Natural Gas Geoscience[J], 2022, 33(9): 1509-1517 doi:10.11764/j.issn.1672-1926.2022.04.003

0 引言

自1945年Arps^［1-2］通过引入损失比建立起3类油气藏产量递减曲线模型，即指数递减模型、双曲递减模型以及调和递减模型以来，围绕着Arps递减模型的研究与扩展应用一直是国内外专家和学者研究的热点。早期国内外专家侧重于Arps递减模型的推广应用研究，如陈元千^［3-5］将Arps递减模型与定容气藏物质平衡方程相结合，建立了识别定容气藏类型的新方法，同时提出了采用试凑法求解模型参数，并建立诺模图用于油藏类型划分与动态指标计算。俞启泰^［6-7］将Arps产量递减模型与水驱油藏特征曲线相结合，在定产液量的条件下首次建立了水驱特征曲线与递减曲线的联系，并在水驱油藏动态分析中广泛使用。蒋立江等^［8］将双曲递减模型进行改进后用于四川盆地天然气产量预测。胡允栋^［9］提出产量递减服从指数分布，将Arps产量递减模型向统计学方面扩展，并考虑产量上升和稳产的情况，首次提出了反正切微分分布模型，极大地扩展了Arps产量递减理论。李传亮等^［10］对众多矿场资料进行统计分析，建立了产量递减规律的一般性诊断方法，将Arps递减模型递减指数的取值范围扩大，并将产量递减模型归结为凹型、凸型、直线型3类模型。俞启泰^［11］通过分析总结Arps产量递减模型的性质，又提出了一种新型油气藏产量递减曲线，并弥补了Arps双曲递减模型不遵守物质守恒的缺陷。随着油气田开发市场化推进，Arps产量递减模型与经济评价相互结合，目前已经成为全球SEC储量商品价值评价的行业标准之一^［12］，同时在工程、工艺措施后评估中，董伟等^［13］以Arps产量递减理论为基础，建立了定量评价开发措施效果的累计产量曲线方法。王怒涛等^［14］以Arps递减模型为基础，通过数学变换提出了有理式型的产量递减模型，并将该模型应用于非常规气藏。与此同时，FETKOVICH^［15］在梳理前人不稳定渗流理论研究成果的基础上，结合Arps产量递减模型，通过引入无因次时间与无因次产量率先建立了递减曲线典型图版进行油气藏产量递减分析与储层参数求取，并认为定流压生产条件下不同类型油气井在边界流阶段无因次时间与无因次产量汇聚成一条指数递减曲线，进而赋予Arps产量递减模型中指数递减模型以渗流意义。陈新彬等^［16］从相对渗透率曲线和物质平衡原理出发，推导并论证了两相水驱油藏Arps产量递减特征是由于相对渗透率曲线形态造成的，从而从两相渗流的角度对Arps产量递减模型的渗流机理进行了解释。陈元千等^［17］则从大量矿产数据出发，通过建立经验统计数学模型对Arps产量递减模型的微分方程进行了理论研究，进一步强化了该模型是经验统计模型。

综上所述，尽管Arps产量递减理论在油气藏评价与开发中广泛用于分析油气井产量递减规律分析，并且日趋完善，但仍存在2个方面的问题：一方面是不同地质条件下Arps递减模型参数的物理意义尚未明确，即渗流机理不清楚，进而限制了该模型在反演地层参数方面的应用；另一方面Arps双曲递减模型存在物质不守恒问题^［9］，并且在非常规气藏中递减指数出现大于1的情况^［18］，这就与传统的递减指数取值范围在0~1之间的认识存在矛盾，但却在油气井开发指标预测中频繁使用，其根本原因在于双曲递减缺乏渗流层面的解释。由于在实际油气藏开发过程中油气井可采储量普遍具有有限性，并且实际油气藏普遍采用先定产后定压的方式开采，油气井在边界流晚期普遍具有长时间的递减特性，因此本文拟以有界储层边界流晚期为研究阶段，基于Hiles and Mott渗流模型，开展油气藏产量递减模型研究，以期从渗流机理入手解释上述2个方面的问题，进而丰富并完善Arps产量递减理论，更好地服务于油气藏评价与开发，尤其对深入认识致密气藏产量递减规律具有重要意义。

1 基于Hiles and Mott渗流机理的有界储层产量递减微分方程

1.1　基于Hiles and Mott渗流机理的拟稳态产能方程

油气在地下多孔介质中渗流规律按渗流速度与压力梯度的关系，可以分为低速非达西流、达西流以及高速非达西流，可近似的采用Hiles and Mott流模型统一描述为^［19］：

v = \frac{q_{r}}{2 π r h} = c {(\frac{\partial p}{\partial r})}^{n}

（1）

其中：当 $n = 1$ 时，Hiles and Mott渗流模型为达西流动；当 $n = 0.5 ~ 1$ 时，Hiles and Mott渗流为高速非达西渗流；当 $n = 0.5$ 时，Hiles and Mott渗流模型为紊流模型；当 $n > 1$ 时，Hiles and Mott渗流为低速非达西渗流。假设油气藏模型为均质圆形封闭模型，位于圆形中心有口油气井，油气井采用定产生产的方式，生产时间足够长进入拟稳态，对于封闭油气藏进入边界流后主要通过岩石及自身的弹性能作为驱动能量，圆形边界地层半径 $r ~ r_{e}$ 范围内可排出流体体积满足^［20］：

V_{r} = π φ ({r_{e}}^{2} - r^{2}) h C_{t} (p_{i} - {\bar{p}}_{r})

（2）

排出流体总体积满足：

V = π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} (p_{i} - \bar{p})

（3）

通过半径为 $r$ 时的任一截面的流量为：

q_{r} = \frac{d V_{r}}{d t} = - π φ ({r_{e}}^{2} - r^{2}) h C_{t} \frac{d {\bar{p}}_{r}}{d t}

（4）

根据式（4），则定产与定压条件下油气井产量均满足：

q = q (t) = \frac{d V}{d t} = - π φ ({r_{e}}^{2} - r_{_{w}}^{2}) h C_{t} \frac{d \bar{p}}{d t}

（5）

由于研究阶段为拟稳态阶段，即：

\frac{d {\bar{p}}_{r}}{d t} = \frac{d \bar{p}}{d t} = \frac{d p_{w f}}{d t}

（6）

由式（3）—式（5）得：

q_{r} = \frac{{r_{e}}^{2} - r^{2}}{{r_{e}}^{2} - r_{w}^{2}} q

（7）

因为 $r_{e} > > r_{w}$ ， ${r_{w}}^{2}$ 可以忽略不计，则：

q_{r} = \frac{{r_{e}}^{2} - r^{2}}{{r_{e}}^{2}} q

（8）

由式（1）、式（8）整理得：

\frac{\partial p}{\partial r} = {(\frac{1}{2 π h c {r_{e}}^{2}})}^{\frac{1}{n}} {(\frac{{r_{e}}^{2} - r^{2}}{r})}^{\frac{1}{n}} q^{\frac{1}{n}}

（9）

令 $E = \int_{r_{w}}^{r_{e}} {(\frac{1}{2 π h c {r_{e}}^{2}})}^{\frac{1}{n}} {(\frac{{r_{e}}^{2} - r^{2}}{r})}^{\frac{1}{n}} d r$ ，则：

p_{e} = p_{w f} + E q^{\frac{1}{n}}

（10）

令：

M = \int_{r_{w}}^{r_{e}} \frac{1}{π (r_{e}^{2} - r_{w}^{2})} {(\frac{1}{2 π h c {r_{e}}^{2}})}^{\frac{1}{n}} {(\frac{{r_{e}}^{2} - r^{2}}{r})}^{\frac{1}{n}} 2 π r d r

，

则：

\bar{p} = p_{w f} + M q^{\frac{1}{n}}

（11）

式（11）即为基于Hiles and Mott渗流模型的拟稳态条件下的油气井产能方程。

1.2　拟稳态条件下定流压等值渗流阻力模型与产量递减微分方程

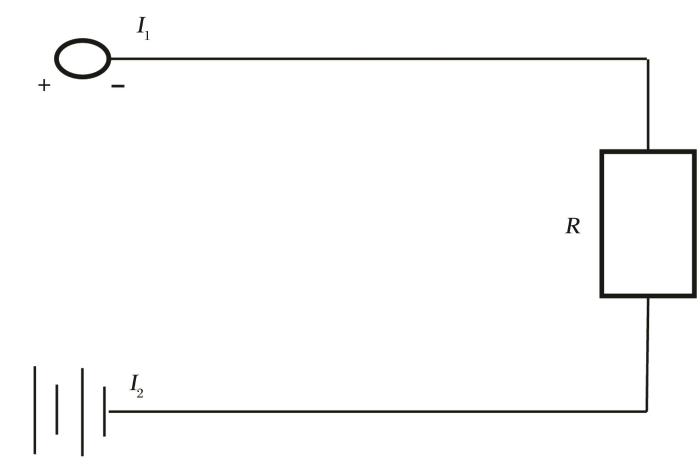
对于油气井拟稳态条件下，利用相似性原理^［21］，可以等效为如图1所示的电路模型图。图1中 $I_{1}$ 端输入电压 $U_{1}$ 为 $\bar{p}$ ， $I_{2}$ 端输入电压 $U_{2}$ 为 $p_{w f}$ ，且满足 $\frac{d U_{1}}{d t} = \frac{d U_{2}}{d t}$ ，电路电流 $I = q$ 。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 拟稳态条件下油气渗流等效电路图

Fig.1 Equivalent circuit diagram of oil and gas seepage under quasi-steady state conditions

根据欧姆定律，结合式（11）：

R = \frac{U_{1} - U_{2}}{I} = \frac{\bar{p} - p_{w f}}{q} = M I^{\frac{1 - n}{n}}

（12）

表明在通电情况下电阻 $R$ 不是恒定电阻而为可变电阻，其数值与电流呈幂相关，满足式（12）。油气井拟稳态条件下定流压生产，相当于 $I_{1}$ 仍然是 $\bar{p}$ ， $I_{2}$ 端更换为一个额定工作电压 $U$ 为 $p_{w f}$ 的直流电源的放电过程，其电流变化规律即为产量变化规律（图2）。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 拟稳态条件下定流压油气渗流等效电路图

Fig.2 Equivalent circuit diagram of oil and gas seepage from the quasi steady state conditions to a constant bottom hole flowing pressure

根据安培环路定律，

u (t) - U = R i (t)

（13）

分别用油气井对应量代换，结合式（12）得：

\bar{p} - p_{w f} = M q {(t)}^{\frac{1}{n}}

（14）

即拟稳态阶段采用定流压生产的生产方式，变产量方程形式上也满足式（11），结合式（5）对时间求导：

\frac{1}{- π φ ({r_{e}}^{2} - {r_{w}}^{2}) h M C_{t}} = \frac{1}{n} q {(t)}^{\frac{1 - 2 n}{n}} \frac{d q (t)}{d t}

（15）

该方程即为基于Hiles and Mott渗流规律的油气井拟稳态条件下采用定流压生产的产量递减微分方程。

2 与Arps递减模型的关系及渗流意义

根据式（1）， $n = 1$ 时，令 $c = \frac{k}{u}$ ，Hiles and Mott渗流规律变为达西定律，重新推导式（7）—式（11）得：

E = (\frac{u}{2 π h k}) (L n \frac{r_{e}}{r_{w}} - \frac{1}{2}), M = (\frac{u}{2 π h k}) (L n \frac{r_{e}}{r_{w}} - \frac{3}{4}), q_{0} = ({\bar{p}}_{0} - p_{w f}) / M

（16）

联立式（15）、式（16）分离变量求解得：

q (t) = q_{0} e^{\frac{- 2 k (t - t_{0})}{u ϕ C_{t} ({r_{e}}^{2} - {r_{w}}^{2}) [L n (\frac{r_{e}}{r_{w}}) - \frac{3}{4}]}}

（17）

令 $D_{0} = \frac{2 k}{u ϕ C_{t} ({r_{e}}^{2} - {r_{w}}^{2}) [L n (\frac{r_{e}}{r_{w}}) - \frac{3}{4}]}$ ，则：

q (t) = q_{0} e^{- D_{0} (t - t_{0})}

（18）

显然与Arps递减模型中指数递减模型具有一致性^［1］，值得注意的是这里的指数递减模型与FETKOVICH^［15］提出的指数递减模型形式上具有一致性，但其含义差距较大，FETKOVICH^［22］提出的模型中使用的产能方程是提前假设的产能方程并且没有理论条件论证其存在的条件，同时其递减模型中的初始递减率只与无阻流量和储量有关，而且其指数递减模型的存在条件是投产初期即采用定流压生产的方式，并且具有不同的初始递减率。

当 $n \neq 1$ 时，对式（15）进行分离变量积分得：

q (t) = q_{0} [1 - \frac{1 - n}{π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} M} (t - t_{0}) {q_{0}}^{\frac{n - 1}{n}}]^{\frac{n}{1 - n}}

（19）

根据式（19），当 $0.5 < n < 1$ 时， $1 - n > 0$ ， $\frac{n}{1 - n} > 0$ ，则式（19）满足幂律递减。

当 $n = 0.5$ 时，即流体渗流满足纯紊流模式时，代入式（19）得：

q (t) = q_{0} - \frac{1}{2 π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} M} (t - t_{0})

(20)

令 $a = \frac{1}{2 π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} M}$ ，则：

q (t) = q_{0} - a (t - t_{0})

（21）

表明流体渗流以紊流渗流形式为主时，油气井定产生产达到拟稳态后采用定流压生产，产量遵循直线递减。

当 $n > 1$ 时， $n - 1 > 0$ ，对式（19）进行变形得：

q (t) = q_{0} [1 + \frac{n (n - 1) / n}{π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} M} (t - t_{0}) {q_{0}}^{\frac{n - 1}{n}}]^{- \frac{n}{n - 1}}

（22）

不妨令

n^{'} = \frac{n - 1}{n}, D_{0} = \frac{n}{π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} M} {q_{0}}^{\frac{n - 1}{n}}

（23）

代入式（22）得：

q (t) = q_{0} [1 + D_{0} n^{'} (t - t_{0} {)]}^{- \frac{1}{n^{'}}}

（24）

显然当 $0 < n^{'} < 1$ 时，与Arps递减模型中双曲递减模型表达式与取值上均具有一致性。进而表明有界储层达到拟稳态条件下采用定流压生产产量递减遵行双曲递减的渗流机理是流体低速非达西流的性质造成的。特别的当 $n \to \infty, n^{'} \to 1$ 时，即：

q (t) = q_{0} / [1 + D_{0} (t - t_{0})]

（25）

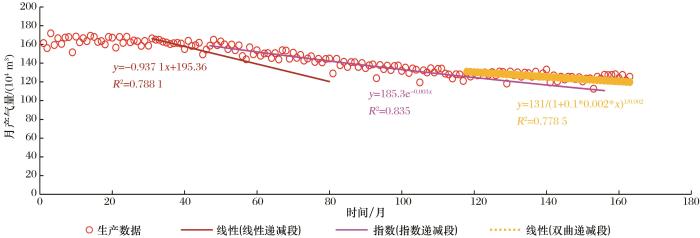
此时产量递减模型与Arps提出的调和递减相吻合，由此可见由Hiles and Mott渗流规律出发，调和递减模型是一种极限模型，从而为Arps调和递减模型储量具有无界性提供了一种渗流机理解释。综上，油气井在遵循不同渗流规律条件下，具有不同的产量递减规律，以川西某典型井为例，该井持续生产长达13 a，从产量递减曲线可以看出，该井具有直线递减、指数递减、双曲递减等多个递减阶段（图3）。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 典型井分阶段递减曲线特征

Fig.3 Characteristic diagram of phased decline curve for typical wells

同时根据式（23）可以得出：

D_{0} = \frac{1 / (1 - n^{'})}{π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} M} {q_{0}}^{n^{'}}

（26）

即低速非达西流采用双曲递减表征的3个参数之间具有非线性相关性，并且其初始递减率与油气井定产达到拟稳态产量 $q_{0}$ 有关，表现为油气井工作制度越高，后期定流压开采产量递减越快，显然这与实际油气藏开发具有一致性［以中江气田为例，气藏工作制度大于5×10⁴m³/d的气井产量与初始递减率呈幂相关（35口），如图4所示］。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 中江气田不同工作制度下气井初始递减率相关图

Fig.4 Correlation diagram of initial decline rate of gas wells under different working systems in Zhongjiang Gas Field

对式（24）积分，结合式（23）得到：

\int_{t_{_{0}}}^{t} q (t) d t = - \frac{n q_{0} [1 + D_{0} \frac{n - 1}{n} (t - t_{0} {)]}^{(- \frac{1}{n - 1})}}{D_{0}} |_{t_{o}}^{t}

（27）

因为 $n > 1$ ，所以 $n - 1 > 0$ ， $t - > \infty$ ，由式（23）得：

\int_{t_{_{0}}}^{\infty} q (t) d t = \frac{n q_{0}}{D_{0}}

（28）

事实上，不妨设拟稳态定流压生产时间 $t_{0}$ 时刻已累计产出量为 $V_{0}$ ，对应时刻地层平均地层压力为 ${\bar{p}}_{0}$ ，由式（3）得：

V_{0} = π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} (p_{i} - {\bar{p}}_{0})

（29）

联立式（3）、式（24）、式（26）得：

\int_{0}^{\infty} q (t) d t = \int_{0}^{t_{0}} q_{0} d t + \int_{t_{0}}^{\infty} q (t) d t = V_{0} + \frac{n q_{0}}{D_{0}}

（30）

联立式（14）、式（23）、式（29）、式（30）得：

\frac{\int_{0}^{t_{o}} q_{0} d t + \int_{t_{o}}^{t} q (t) d t}{π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} (p_{i} - p_{a})} = \frac{p_{i} - p_{w f}}{p_{i} - p_{a}}

（31）

因为拟稳态条件下采用定流压生产，所以t->∞，废弃压力 $p_{w f} (> 0)$ 趋近于 $p_{a}$ ，显然式（31）趋近于1，与学术界认为Arps双曲递减不满足质量守恒定律^［9］相违背，原因在于后者仅从数学模型的角度对Arps递减模型进行归一化理论推导，忽略了其渗流物理意义。

3 模型应用

3.1　渗流规律判定

从Hiles and Mott渗流模型出发，油气井定产生产达到拟稳态后产量递减由于受储层物性特征及微观结构特征影响，产量递减具有指数递减、幂律递减（包括线性递减）以及双曲递减（极限条件为调和递减）等特征，分别对应达西线性流、非达西高速过渡流（含紊流）以及非达西低速流（含极限低速），因此可以根据曲线特征进行油气藏渗流特征分析。其判别方程可以根据式（15）建立，采用Arps提出的损失比，即：

D = - \frac{d q (t)}{q (t) d t}

（32）

令 $\frac{1}{π φ ({r_{e}}^{2} - {r_{w}}^{2}) h M C_{t}} = A$ ，由式（15）得：

n A = q {(t)}^{\frac{1 - n}{n}} D

（33）

对式（33）进行对数变换得：

L n D = L n (n A) + \frac{n - 1}{n} L n [q (t)]

（34）

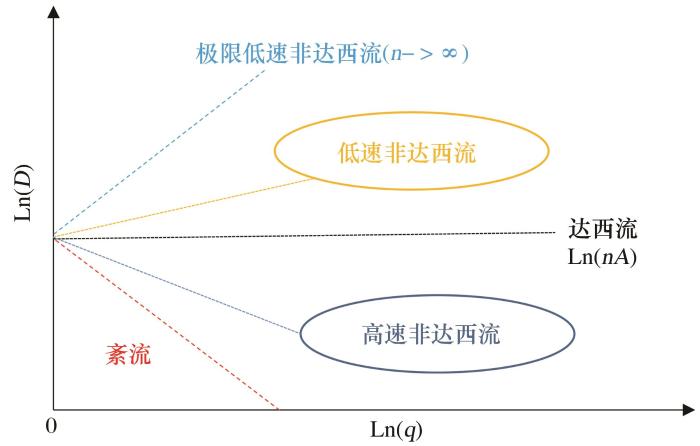
即在双对数坐标中， $D - q$ 为一条直线（图5），不妨把该直线称为产量递减特征曲线，与李传亮等^［10］提出的产量递减规律诊断曲线形式上具有一致性。其中流体为达西流体时，特征曲线为一条水平直线（ $n = 1$ ）。当渗流流体为高速非达西流时（ $0.5 < n < 1$ ），特征曲线表现为一条斜率向下的直线；当 $n = 1 / 2$ 时，对应的斜率为-1的特征曲线是流体紊流规律曲线。当流体为低速非达西流时（ $n > 1$ ），特征曲线为一条斜率向上倾斜的直线且斜率趋近于1，因此可以通过特征曲线判别流体的渗流规律。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 边界流晚期拟稳态条件下油气井渗流特征诊断图

Fig.5 Diagnosis diagram of seepage characteristics of oil and gas wells under quasi steady state conditions at the late stage of boundary flow

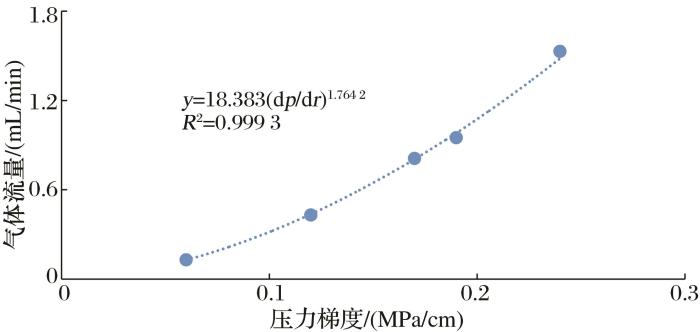
以川西凹陷某致密气藏为例，通过对某井开展岩样渗流实验（岩心为典型的河道砂岩，实验分析孔隙度为8%，渗透率为0.08×10^-3μm²），相关数据见表1。采用幂函数进行拟合，得到渗流速度与压力梯度关系为（图6）：

v = 18.383 {(\frac{d p}{d r})}^{1.764 2}

（35）

表1 气井岩心渗流实验数据统计

Table 1 Statistical table of experimental data of gas well core seepage

压力梯度/（MPa/cm）	0.06	0.12	0.17	0.19	0.24
气体流量/（mL/min）	0.13	0.43	0.81	0.95	1.53

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 岩心渗流实验流量—压力梯度拟合图

Fig.6 Fitting diagram of flow-pressure gradient for core seepage experiment

表明该岩心储层条件下气井渗流满足Hiles and Mott渗流模型，即低速非达西流。

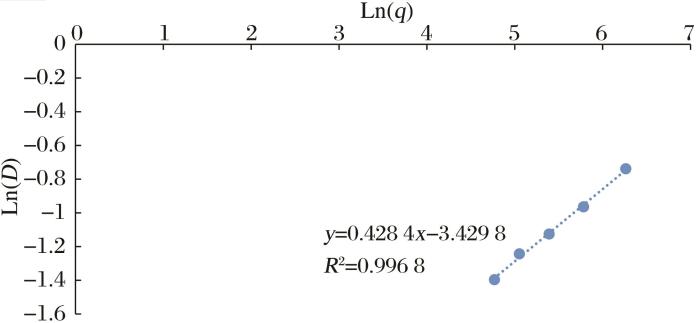
目前该井已进入低产低压阶段（压力变化较小，可近似看作定流压生产），其生产数据如表2所示。采用产量递减特征曲线进行诊断，斜率为正，表明该气井目前流体渗流遵循低速非达西流，与该气井岩心渗流实验结论一致。同时采用线性回归拟合 $L n (D) - L n (q)$ 如图7，利用直线斜率（ $n'$ ）与Hiles and Mott渗流指数（ $n$ ）之间的关系：

n = \frac{1}{1 - n^{'}}

（36）

表2 气井（对应表1）生产数据

Table 2 Production data table of gas wells(corresponding to Table 1)

年份	年流量/（10⁴m³/a）	递减率/a^-1	Ln（q）	Ln（D）
2016	1 005.30
2017	525.47	0.477 297	6.264 294	-0.739 62
2018	325.17	0.381 185	5.784 346	-0.964 47
2019	219.75	0.324 206	5.392 479	-1.126 38
2020	156.39	0.288 341	5.052 322	-1.243 61
2021	117.72	0.247 221	4.768 339	-1.397 47

新窗口打开| 下载CSV

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 气井产量递减特征曲线

Fig.7 The production decline characteristic curve of a gas well

计算 $n$ 为1.749 8，对比渗流实验拟合的Hiles and Mott渗流指数（1.764 2），误差较小，进一步验证了式（23）、式（24）描述的等效双曲递减曲线指数与Hiles and Mott渗流指数之间的关系的正确性，由于岩心实验尺度较小，气井递减反映的是井控范围的储层综合条件，因此其数值存在一定的差异性。

此外，产量递减模型常用于油气藏产量预测与可采储量评价，由于本文所研究模型与Arps递减模型形式上具有一致性，同时产量递减特征曲线与李传亮等^［10］提出的递减规律曲线形式上也具有一致性，因此模型参数求解与应用可参考文献［4-5］、［10］、［17］，本文不再赘述。

3.2　储层参数反演

根据上述递减模型的推导过程可以看出，模型产生的基础条件是气井拟稳态条件下的定流压生产。油气井实际生产普遍采用先定产后定压的生产方式，并且在定产期间为了实现气井稳产具有调整工作制度的情况，这就破坏了油气井实现拟稳态的条件，然而根据渗流力学压力叠加原理建立的变产量生产瞬态方程，当最后一次油气井生产制度足够长时间条件下，油气井调产生产模式造成的影响可以忽略^［19-20］，因此上述递减模型在实际生产过程中具有通用性。油气藏实际开发中，等效渗流半径是制定井网、井距的重要参考参数，目前普遍采用现代递减分析方法求取^［22-24］，根据上述产量递减模型也可以求取，由式（11）与式（23）得：

D_{0} = \frac{n}{π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t} ({\bar{p}}_{0} - p_{w f})} q_{0}

（37）

根据式（3）：

{\bar{p}}_{0} = p_{i} - \frac{V_{0}}{π φ ({r_{e}}^{2} - {r_{w}}^{2}) h C_{t}}

（38）

联立式（37）、式（38）得：

r_{e} = \sqrt[]{(\frac{n q_{o}}{D_{0}} + V_{0}) / (π ϕ h c_{t} (p_{i} - p_{w f})) + r_{w}^{2}}

（39）

实际油气藏开发中通过拟合递减曲线获取递减模型参数，采用Hagedorn-brown方法计算井底流压，同时结合测井解释成果，利用式（39）可以计算油气井泄气半径，进而为油气井等效泄气半径的求取提供了一种新的简便方法。对表2中气井采用式（38）计算等效泄气半径为217 m，与采用PALACIO等^［24］计算等效泄气半径（212 m）相当。

4 结论

（1）基于Hiles and Mott渗流规律，建立了有界储层边界流晚期产量递减微分方程，通过理论推导明确了不同Hiles and Mott渗流指数对应条件下的产量递减曲线，其中当Hiles and Mott渗流指数介于0.5~1之间时，产量递减曲线为幂律递减；当Hiles and Mott渗流指数为0.5时，产量递减曲线为直线递减；当其为1时为指数递减；当Hiles and Mott渗流指数大于1时为双曲递减；当Hiles and Mott渗流指数趋近于无穷大时无限接近于调和递减，即当其大于等于1时，有界储层边界流晚期产量递减形式上与Arps递减具有一致性，并且模型参数之间具有非线性相关性，双曲递减模型遵循质量守恒定律，进而为Arps产量递减的渗流机理提供了一种理论依据。

（2）通过引入Arps提出的损失比，建立了产量递减特征曲线，该曲线与李传亮等^［10］研究的产量递减诊断曲线形式上保持一致性，即在双对数坐标条件下损失比与产量呈现为一条直线，利用该性质结合Hiles and Mott渗流模型为油气井渗流规律提供了一种判别模型，即当该直线为水平直线时，流体渗流遵循达西定律；当直线斜率为负时，流体渗流遵行高速非达西定律；当直线斜率为正时，流体渗流遵行低速非达西定律。

（3）实例分析表明，采用岩心实验渗流规律分析与采用产量递减特征曲线诊断结果较为吻合，进一步验证了Arps产量递减模型具有渗流意义，对于有界储层条件其递减曲线类型取决于渗流定律，进而为使用Arps递减模型开展地层参数反演奠定了理论基础。

符号注释： $v$ 为渗流速度，m/s； $q_{r}$ 为半径为 $r$ 处流体流量，10⁴m³/d； $r$ 为渗流半径，m； $h$ 为储层厚度，m； $c$ 为Hiles and Mott渗流系数； $n$ 为 Hiles and Mott渗流指数； $V_{r}$ 为半径 $r ~ r_{e}$ 范围内排出流体体积，m³； $φ$ 为孔隙度，无量纲； $r_{e}$ 为圆形边界半径，m； $C_{t}$ 为综合压缩系数，MPa^-1； $p_{i}$ 为原始地层压力，MPa； ${\bar{p}}_{r}$ 为半径 $r ~ r_{e}$ 范围内平均地层压力，MPa； $V$ 为半径 $r_{w} ~ r_{e}$ 范围内排出流体体积，m³； $\bar{p}$ 为半径 $r_{w} ~ r_{e}$ 范围内平均地层压力，MPa； $r_{w}$ 为井筒半径，m； $t$ 为时间，d； $q_{r}$ 为半径 $r$ 处流体产量，m³/d； $q$ 为定产量井筒处流体流量， m³/d； $q (t)$ 为变产量井筒处流体流量，m³/d； $p_{w f}$ 为井底流压，MPa； $p_{e}$ 为边界处地层压力，MPa； $U$ 为电压，V； $I$ 为电流，A； $R$ 为电阻， $Ω$ ； $u (t)$ 为瞬时电压，V； $i (t)$ 为瞬时电流，A； $k$ 为渗透率，10^-3µm²； $u$ 为流体黏度，Pa·s； $q_{0}$ 为产量递减期初始产量（定产期产量），m³/d； $t_{0}$ 为初始递减时间，d； $D_{0}$ 为Arps递减模型初始递减率，d^-1； $D$ 为递减率，d^-1； ${\bar{p}}_{0}$ 为 $t_{0}$ 时刻平均地层压力，MPa； $V_{0}$ 为 $t_{0}$ 时刻流体累计产出量，m³； $p_{a}$ 为废弃地层压力，MPa。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ARPS J J. Analysis of decline curve［J］.Transactions of the AIME，1945，160（1）：228-247.

[本文引用: 2]

[2]

ARPS J J. Estimation of primary oil reserves［J］.Transactions of the AIME，1956，207（1）：182-191.