0 引言
体积压裂是实现深层页岩气开发的关键手段。体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素。目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] 。王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布。针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面。
以上对复杂缝网渗流的研究存在以下问题:缺乏对缝网真实特征的描述,部分学者只对其做了定量的研究,同时页岩气渗流机理也考虑不全面。基于分形理论的裂缝尺度升级也局限于单裂缝到简单多裂缝,没有考虑到缝网的真实分布和非均质性。为了进一步解决以上问题,本文将围绕缝网的真实结构特征,通过CT扫描人工造缝岩心,经过二值化处理并计算分形维数,通过蒙特卡洛随机建模算法统计裂缝相关参数;同时基于流量等效原理,在直角坐标系中正交分解缝网中的每一条裂缝,用x 方向和y 方向的2簇平行裂缝等效代替原有的复杂非均质缝网;最后综合考虑页岩气的黏性流、克努森扩散、表面扩散,进一步考虑缝宽动态变化,建立单裂缝流量方程;通过分形理论尺度升级,将单裂缝扩展到平行裂缝簇,联立广义达西定律,得到x 方向和y 方向的等效渗透率,最后耦合得到非均质缝网渗透率模型。本文提供了一个描述复杂缝网的方法,同时进一步揭示了深层页岩气在缝网中的渗流机理,为深层页岩气藏体积压裂缝网改造区的渗透率动态表征提供理论指导。
1 非均质缝网描述
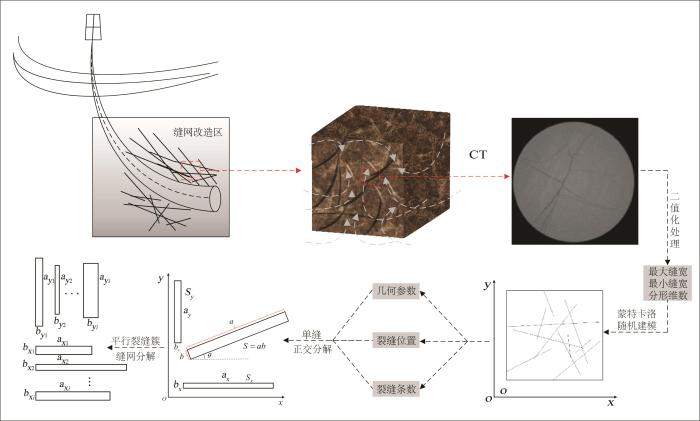
深层页岩气藏体积压裂改造后近主裂缝面处的裂缝网络分布十分复杂,会形成一个非均质的缝网改造区[5 ] ,页岩气的渗流机理也因为缝网区的非均质分布变得很复杂,合理并准确的描述裂缝网络变得十分重要。由于实际缝网改造区的岩心不易获得,所以用人工造缝岩心代替SRV 区域的真实结构,通过CT扫描并在此基础上确定裂缝条数、裂缝位置、裂缝的几何参数(倾角、宽度、裂缝位置等),运用蒙特卡洛随机建模方法生成随机裂缝网络,通过对缝网裂缝二值化处理,最后生成裂缝网络[2 ,17 ] 。对于得到的离散二维裂缝网络,基于流量等效原理[18 ] ,在直角坐标系中对其进行正交分解,得到x 方向和y 方向的两簇平行裂缝,裂缝的长度变化范围远小于宽度变化,为了简便计算,可对裂缝长度取平均值,分解过程如图1 所示:
图1
图1
缝网改造区渗流示意
Fig.1
Schematic diagram of seepage flow in fracture network stimulated area
a x i = a i ⋅ c o s θ i (1)
a y i = a i ⋅ s i n θ i (2)
a x ¯ = 1 n ∑ i = 1 n a x i (3)
式中:a x i i 条裂缝在x 方向长度分量,m;a i i 条裂缝长度,m;θ i i 条裂缝与x 方向夹角,°; a x ¯ x 方向裂缝长度平均值,m;a y i i 条裂缝在y 方向长度分量,m;a y ¯ y 方向裂缝长度平均值,m。
b x i = b i ⋅ s i n θ i (4)
b y i = b i ⋅ c o s θ i (5)
b x m a x b y m a x b x m i n b y m i n 2 × 2 = m a x b x i m a x b y i m i n b x i m i n b y i 2 × 2 (6)
式中:bxi 为第i 条裂缝在x 方向宽度分量,m;bi 为第i 条裂缝宽度,m;byi 为第i 条裂缝在y 方向宽度分量,m;bx max 为x 方向最大缝宽,m;bx min 为x 方向最小缝宽,m;by max 为y 方向最大缝宽,m;by min 为y 方向最小缝宽,m。
2 缝网表观渗透率
为了研究深层页岩气在复杂缝网中的渗流机理,本文基于流量等效原理将二维复杂缝网正交分解为x 、y 方向的平行裂缝簇。从单裂缝出发,考虑地应力变化对缝宽变化的影响[16 ] ,通过页岩气的黏性流、克努森扩散、表面扩散建立单缝流量方程。通过分形理论将尺度升级到平行裂缝簇,耦合得到缝宽动态变化下的缝网渗透率计算模型。
2.1 单缝流量方程
地应力变化引起的缝宽变化由裂缝压缩性、基质压缩性、气体解吸附性三部分共同作用产生,所以由压力变化导致的页岩裂缝宽度总变化量为[19 -21 ] :
Δ b t = b 0 c f ( p p - p p 0 ) + a 0 ( 1 - 2 υ ) E ( p p - p p 0 ) -
a 0 S L p L ( p L + p p 0 ) ( p L + p p ) ( p p - p p 0 ) (7)
式中:E 为岩石杨氏模量,MPa; υ 为泊松比,无量纲;c f -1 ;p L p p p p 0 λ 为分子自由程,m。
K n b = λ b + Δ b t (8)
当气体克努森数K n b -3 ,页岩气体满足黏性流动,流量方程可用Hagen-Poiseuille方程表达为:
J v s = - A ( ζ b ) ϕ τ a ( b + Δ b t ) 3 12 μ r p M R T ( 1 + α K n b ) ⋅ ( 1 + 6 K n b 1 - m K n b ) d p d a (9)
A ( ζ b ) = 1 - 192 ζ b π 5 ∑ i = 1,3 , 5 ∞ t a n h ( i π ζ b / 2 ) i 5 (10)
式中:J v s A ( ζ b ) τ
当K n b
J k = - B ( ζ b ) ϕ τ ρ ( b + Δ b t ) 3 ( M 2 π R T ) 0.5 d p d a (11)
B ( ζ b ) = ζ b 2 L n ( 1 ζ b + 1 + 1 ζ b 2 ) + ζ b L n ( ζ b + 1 + ζ b 2 ) - ( ζ b 2 + 1 ) 3 / 2 3 + 1 + ζ b 3 3 (12)
式中:J k 3 /s;B ( ζ b )
页岩气体在小尺度裂缝中流动时同时还伴随着沿吸附壁面的运移,即表面扩散作用,气体表面扩散流量方程为:
J s u r f a c e = - a b M D s ρ C s m a x p L ( p + p L ) 2 d p d a (13)
式中:J s u r f a c e 3 /s;D s 为表面扩散系数,m2 /s;C smax 为表面吸附气最大浓度,mol/m3 。
2.2 平行裂缝簇流量方程
基于储层裂缝具有高度的自相似性,通过分形理论对单裂缝进行尺度升级,从微观单裂缝求和得到宏观裂缝网络的总流量方程[12 ] 。
根据分形理论,缝网中的裂缝宽度大于等于b 的裂缝条数表示为[22 ] :
N = b m a x b D f (14)
d N d b = - D f b m a x D f b - D f + 1 (15)
式中:N 为分形集合中裂缝宽度大于等于b 的裂缝条数,无量纲;b max 为分形集合中最大裂缝宽度,m;D f 为裂缝宽度分形维数,无量纲。
Q i = - ∫ b m i n b m a x J i d N (16)
式中:i ∈ v s , k , s u r f a c e i 表示流动机理。
将式(9)、式(11)、式(13)、式(14)、式(15)代入式(16)中可以分别得到页岩气黏性流、克努森扩散、表面扩散的平行裂缝簇总流量方程如下:
Q v s = - ∫ b m i n b m a x J v s d N = - A ( ζ b ) D f b m a x D f 12 μ r a ϕ τ ρ p M R T d p d a ∫ b m i n b m a x ( b + Δ b t ) 3 b - D f + 1 d b = - A ( ζ b ) D f b m a x D f 12 μ r a ϕ τ ρ p M R T d p d a Δ b t 3 ( b m a x - D f - b m i n - D f ) - D f + 3 Δ b t 2 ( b m a x - D f + 1 - b m i n - D f + 1 ) - D f + 1 + 3 Δ b t ( b m a x - D f + 2 - b m i n - D f + 2 ) - D f + 2 + b m a x - D f + 3 - b m i n - D f + 3 - D f + 3 (17)
Q k = - ∫ b m i n b m a x J k d N = - B ( ζ b ) D f b m a x D f ϕ τ ρ ( M 2 π R T ) 0.5 d p d a ∫ b m i n b m a x ( b + Δ b t ) 3 b - D f + 1 d b = - B ( ζ b ) D f b m a x D f ϕ τ ρ ( M 2 π R T ) 0.5 d p d a Δ b t 3 ( b m a x - D f - b m i n - D f ) - D f + 3 Δ b t 2 ( b m a x - D f + 1 - b m i n - D f + 1 ) - D f + 1 + 3 Δ b t ( b m a x - D f + 2 - b m i n - D f + 2 ) - D f + 2 + b m a x - D f + 3 - b m i n - D f + 3 - D f + 3 (18)
Q s u r f a c e = - ∫ b m i n b m a x J s u r f a c e d N = - a M D f b m a x D f D s ρ C s m a x p L ( p + p L ) 2 d p d a ∫ b m i n b m a x b - D f d b = - a M D f b m a x D f D s ρ C s m a x p L ( p + p L ) 2 d p d a ( b m a x - D f + 1 - b m i n - D f + 1 ) - D f + 1 (19)
式中:Qvs 为平行裂缝簇黏性流动总流量,m3 /s;Qk 为平行裂缝簇克努森流动总流量,m3 /s;Q surface 为平行裂缝簇表面扩散总流量,m3 /s。
综合考虑黏性流、克努森扩散、表面扩散和缝宽动态变化的平行裂缝簇气体总流量方程为:
Q t = Q v s + Q k + Q s u r f a c e (20)
式中:Q t 为考虑缝宽动态变化的平行裂缝簇气体总流量,m3 /s。
2.3 非均质缝网等效渗透率
Q t = - K ⋅ A p ⋅ Δ p μ ⋅ L (21)
对于矩形裂缝,同时考虑孔隙度对裂缝截面积的影响,分形截面积A p [23 ] :
A p = - ∫ b m i n b m a x a b ϕ d N = a b m a x ϕ D f ( 1 - D f ) 1 - b m a x b m i n D f - 1 (22)
D f = 2 + L n ϕ L n b m a x b m i n (23)
式中:A p 为分形裂缝总面积,m2 ;ϕ
将式(22)、式(23)、式(24)、式(27)、式(29)、式(30)代入到式(28)中可得到平行裂缝簇渗透率表达式如下:
K = - μ ϕ ( 1 - D f ) a b m a x D f 1 - b m a x b m i n D f - 1 ( Q v s + Q k + Q s u r f a c e ) (24)
对于x 方向和y 方向的2簇平行裂缝,分别将b x m a x b x m i n a x ¯ b y m a x b y m i n a y ¯ 式(14)—式(24),可以得到2个方向各自的渗透率K x K y [24 ] :
K f = K x 2 + K y 2 2 (25)
式中:K f 为等效缝网表观渗透率,m2 ;Kx 为x 方向平行裂缝簇渗透率,m2 ;Ky 为y 方向平行裂缝簇渗透率,m2 。
通过对正交平行裂缝簇渗透率的耦合,得到缝网等效表观渗透率模型。该模型通过流量等效原理解决了非均质缝网中裂缝的分布问题,同时综合考虑了页岩气的黏性流、克努森扩散、表面扩散和缝宽动态变化,可以更好地对深层页岩气藏体积压裂后缝网改造区的渗流问题进行有效性评价和动态研究。
3 模型验证及其应用
基于流量等效原理和分形理论,本文建立了一个复杂非均质缝网渗透率模型,该模型充分考虑了页岩气在缝网中的黏性流、克努森扩散、表面扩散,同时考虑应力敏感引起的缝宽动态变化,可以更完整地表征深层页岩气藏缝网改造区的渗透率动态变化。为了验证模型的可靠性,本文将该模型与实验结果和理论模型进行对比,本文模型计算基础参数如表1 所示。
3.1 实验验证
朱维耀等[25 ] 曾选取龙马溪组页岩岩样,采用巴西劈裂法进行人工造缝,利用覆压孔渗仪对压裂前后的渗透率进行测量,此处以本文模型计算结果与其进行对比验证,岩样基本参数如表2 所示。
通过对岩样的CT图片进行统计得到缝网中每条裂缝的坐标、几何参数、裂缝条数如表3 所示。
通过对每条裂缝进行正交分解得到2簇平行裂缝,将表3 的统计结果代入式(1)—式(6)可以得到a ¯ x a ¯ y b x m i n b x m a x b y m i n b y m a x x 方向、y 方向、耦合等效渗透率值分别为36.82×10-3 μm2 、40.53×10-3 μm2 、54.76×10-3 μm2 ;实验测得的渗透率值为50.6×10-3 μm2 ,计算结果与实验结果相对误差为8.22%,这说明本文建立的利用正交分解处理复杂缝网的方法具有较好的适用性,能较好地应用于实际的缝网渗透率计算。
3.2 理论模型验证
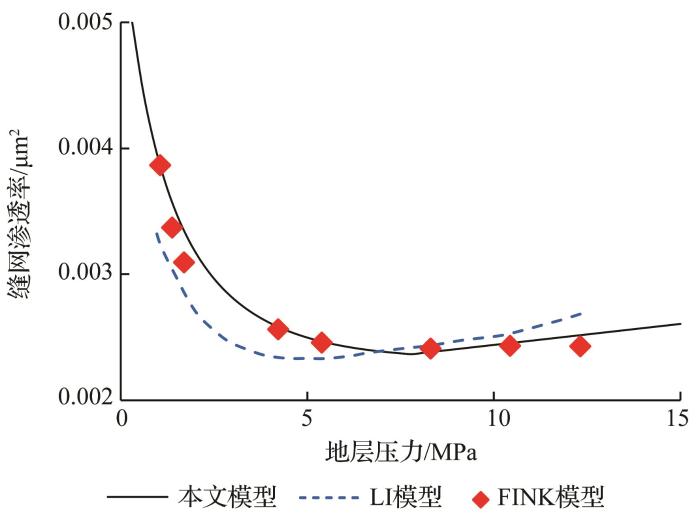
LI等[21 ] 同样考虑应力敏感引起的动态缝宽变化,建立了简单平行多裂缝的渗透率模型,而基于本文模型建立的复杂缝网的等效处理方法,并进一步耦合页岩气在缝网中的多种流动机理得到一个更为全面的复杂缝网渗透率动态表征模型。为了充分说明本文模型的准确性和适用性,将本文计算模型与LI等[21 ] 简单缝网渗透率模型和FINK等[26 ] 实验数据进行对比验证,对比结果如图2 所示。
图2
图2
本文模型理论验证对比
Fig.2
Model verification comparison chart of this paper
由图2 可知,在较高地层压力下,随着地层压力降低,由于应力敏感作用,缝网表观渗透率呈现轻微下降趋势,与LI模型和实验数据一致;在低地层压力下,随着地层压力降低,缝网渗透率迅速增大,这是由于低压下克努森效应、表面扩散对页岩气流动产生很大影响。由于LI模型只考虑了页岩气的黏性流,没有进一步耦合页岩气流动的克努森效应和表面扩散效应,在低压下本文模型渗透率值要略大于李模型,与实验结果更为接近。
3.3 模型应用
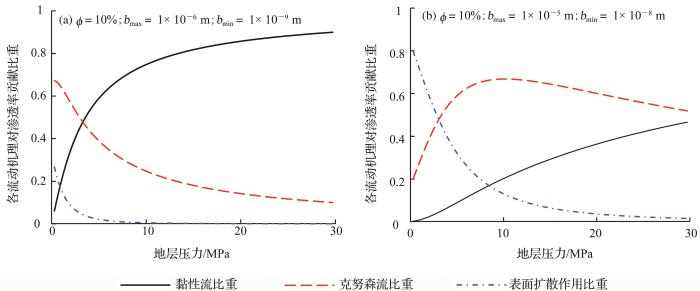
图3 (a)表明,在小尺度缝网中,表面扩散作用对页岩气流动影响相当明显。随着地层压力减小,黏性流比重逐渐减小,克努森扩散比重先增大后减小,表面扩散作用比重呈增大趋势且增大幅度越来越大。该尺度下,在压力小于3 MPa时,表面扩散作用占据主导作用,而在高地层压力时,页岩气流动主要以克努森扩散和黏性流为主;图3 (b)表明,随着缝网尺度的增大,表面扩散作用所占比重有了较大下降,其仅在低地层压力下对缝网渗透率有一定贡献,在地层压力大于10 MPa时,可以忽略不计。黏性流和克努森扩散随地层压力下降,对缝网渗透率的贡献呈现此消彼长趋势,在高地层压力时黏性流占主导地位,是此尺度条件下的页岩气流动的主要方式。
图3
图3
不同流动机理对缝网渗透率贡献
Fig.3
Different flow mechanisms contribution to the permeability of the fractured network
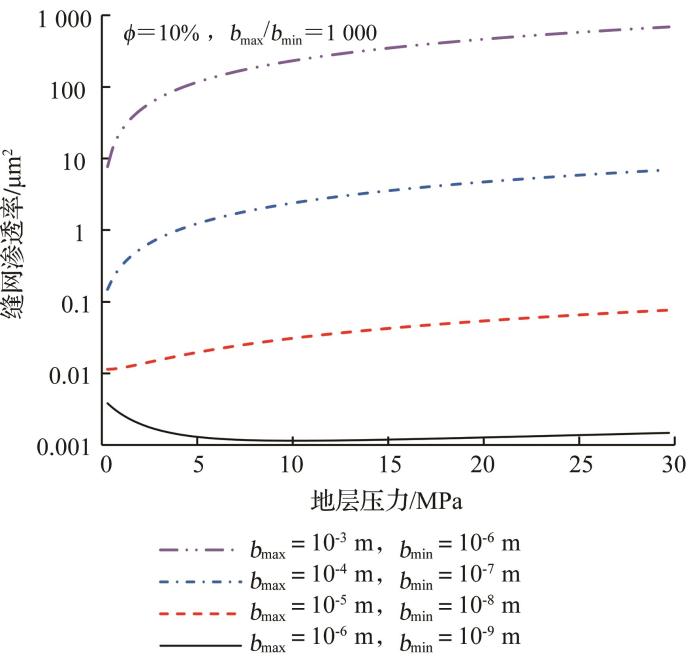
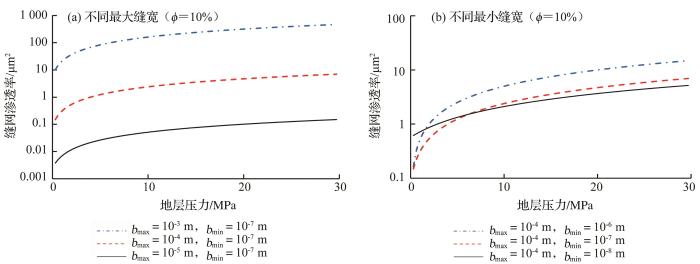
由图4 可知,在缝网裂缝孔隙ϕ b m a x / b m i n
图4
图4
不同尺度下缝网渗透率计算结果
Fig.4
Fracture network permeability for different scales
图5 (a)表明,在缝网裂缝孔隙度ϕ 图5 (b)表明,最小缝宽对渗透率影响相对较小;最小缝宽尺度较大时,最小缝宽增大1个数量级,缝网渗透率增长接近2倍,但在低压下渗透率差异不大;同时尺度较小时,由于表面扩散的作用增强,其渗透率有小幅度的上升,在低压(5 MPa)下甚至比更大尺度时的渗透率大。
图5
图5
不同缝宽下缝网渗透率计算结果
Fig.5
Fracture network permeability for different fracture widths
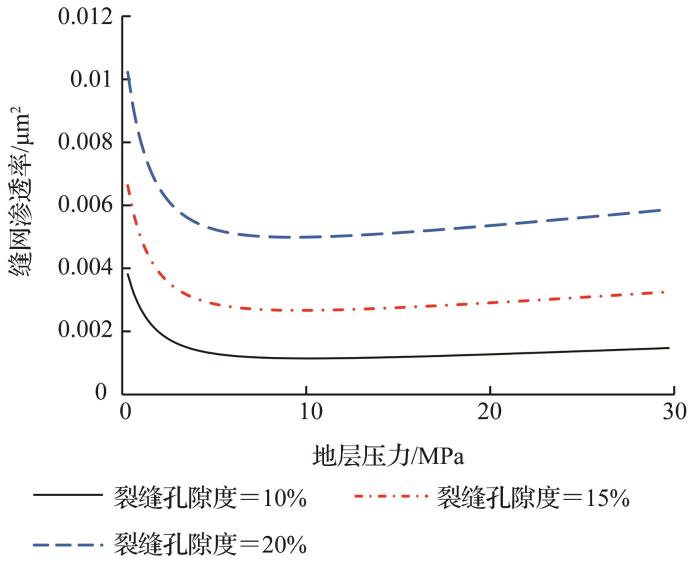
图6 表明,在缝网尺度不变时,裂缝孔隙度对缝网渗透率影响十分显著,裂缝孔隙度增大1倍,缝网表观渗透率增加约1.7倍。这是由于裂缝孔隙度越大,缝网分形维数越大,缝网分布越密集,页岩气的流动通道越多,其渗透率值也越高。
图6
图6
不同裂缝孔隙度对缝网渗透率的影响
Fig.6
Different fracture porosity effect on fracture network permeability
4 结论
(1)本文建立了考虑缝宽动态变化的非均质缝网表观渗透率模型,通过将本文模型与实验数据和理论模型结果对比表明:CT扫描人工造缝岩心和蒙特卡洛随机建模并统计裂缝参数具有合理性;也充分验证了基于流量等效原理分解非均质缝网、耦合页岩气不同流动机理、分形理论尺度升级的可靠性和准确性。
(2)页岩气在小尺度缝网中以表面扩散为主,随着地层压力增大,克努森扩散和黏性流逐渐占领主导地位,表面扩散比重随地层压力增大而减小;随着缝网尺度增大,表面扩散比重下降,表面扩散在地层压力大于10 MPa时可忽略,页岩气的流动机理为黏性流和克努森扩散;大尺度缝网克努森扩散效应随地层压力增大,先增强后减弱,表面扩散和黏性流呈此消彼长的趋势。
(3)小尺度缝网渗透率随地层压力增大先减小后增大,大尺度缝网渗透率与地层压力成正比。小尺度缝网在低压(5 MPa)时表面扩散对渗透率的影响增强,导致在该尺度下的渗透率值有小幅度增大且略大于大尺度缝网;在不同最大缝宽的条件下,最大缝宽增大10倍,缝网渗透率增长接近100倍;在不同最小缝宽的条件下,渗透率增大只在最小缝宽较大时明显。此外,裂缝孔隙度增大1倍,缝网表观渗透率增加1.7倍。
参考文献
View Option
[1]
张世明, 严侠, 孙红霞, 等. 基于离散裂缝模型的裂缝性介质等效渗透率求解新方法[J]. 科学技术与工程, 2014, 14(16): 36-40.
[本文引用: 1]
ZHANG S S, YAN X, SUN H X, et al. An efficient calculation of dquivalent permeability of fractured porous media based on discrete fracture model[J]. Science Technology and Engineering, 2014, 14(16): 36-40.
[本文引用: 1]
[2]
王晨星. 基于复杂裂缝网络页岩气产量研究[D]. 成都: 西南石油大学, 2018.
[本文引用: 2]
WANG C X. Research on Productivity of Fractured Horizontal Wells in Shale Gas Reservoir Based on Complicated Fractured Network[D].Chengdu:Southwest Petroleum University,2018.
[本文引用: 2]
[3]
ROBERTSON E P, CHRISTIANSEN R L. A permeability model for coal and other fractured, sorptive-elastic media[J]. SPE Journal, 2006, 13(3): 314-324.
[本文引用: 1]
[4]
REN L, SU Y, ZHAN S, et al. Progress of the research on productivity prediction methods for stimulated reservoir volume (SRV)-fractured horizontal wells in unconventional hydrocarbon reservoirs[J]. Arabian Journal of Geosciences, 2019, 12(6): 184.
[本文引用: 1]
[5]
CLARKSON C R. Production data analysis of unconventional gas wells: Review of theory and best practices[J]. International Journal of Coal Geology, 2013, 109: 101-146.
[本文引用: 2]
[6]
王文东. 体积压裂水平井复杂缝网分形表征与流动模拟[D].青岛:中国石油大学,2015.
[本文引用: 1]
WANG W D. Fractal-based Multi-stage Hydraulically Fracture Network Characterization and Flow Modeling[D].Qingdao:China University of Petroleum,2015.
[本文引用: 1]
[7]
曲鸿雁,彭岩,刘继山,等.气体吸附对页岩裂缝表观渗透率和页岩气采收率的影响[J].中国科学:技术科学,2018,48(8):891-900.
[本文引用: 1]
QU H Y, PENG Y, LIU J S, et al. Impact of gas adsorption on apparent permeability of shale fracture and shale gas reco-very rate[J]. Scientia Sinica:Technologica,2018,48(8):891-900.
[本文引用: 1]
[8]
吴克柳, 李相方, 陈掌星, 等. 页岩气和致密砂岩气藏微裂缝气体传输特性[J]. 力学学报, 2015, 47(6): 955-964.
[本文引用: 1]
WU K L, LI X F, CHEN Z X, et al. Gas transport behavior through micro fractures of shale and tight gas reservoirs[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(6): 955-964.
[本文引用: 1]
[9]
曾凡辉, 彭凡, 郭建春, 等.考虑页岩缝宽动态变化的微裂缝气体质量传输模型[J].天然气地球科学, 2019, 30(2): 237-242.
[本文引用: 1]
ZENG F H, PENG F, GUO J C, et al.The gas mass transport model considering the dynamic change of micro-fracture width in shale[J].Natural Gas Geoscience,2019,30(2):237-242.
[本文引用: 1]
[10]
KROHN C E. Fractal measurements of sandstone, shales and carbonates[J].Journal of Geophysical Research,1988,93(B4): 3297-3305.
[本文引用: 1]
[11]
MAHAMUD M M, NOVO M F. The use of fractal analysis in the textural characterization of coals[J]. Fuel, 2008, 87(2): 222-231.
[本文引用: 1]
[12]
XIE S, CHENG Q, LING Q, et al. Fractal and multifractal analysis of carbonate pore-scale digital images of petroleum reservoirs[J].Marine and Petroleum Geology,2010,27(2):476-485.
[本文引用: 2]
[13]
LI C, LIN M, JI L, et al. Rapid evaluation of the permeability of organic-rich shale using the 3D intermingled-fractal model [J]. SPE Journal, 2018, 23(6): 2,175-172,187.
[本文引用: 1]
[14]
YU B M, WEI L. Fractal analysis of permeabilities for porous media[J]. AICHE Journal, 2010, 50(1):46-57.
[本文引用: 1]
[15]
LI Y, YU B M. Study of the starting pressure gradient in branching network[J]. Science China Technological Sciences, 2010, 53(9): 2397-2403.
[本文引用: 1]
[16]
李玉丹, 董平川, 周大伟,等.页岩气藏微裂缝表观渗透率动态模型研究[J]. 岩土力学, 2018, 39(S1):42-50.
[本文引用: 2]
LI Y D, DONG P C, ZHOU D W, et al.A dynamic model of apparent permeability for micro fractures in shale gas reservoirs[J]. Rock and Soil Mechanics,2018,39(S1):42-50.
[本文引用: 2]
[17]
曾凡辉, 彭凡, 郭建春, 等. 一种复杂裂缝网络渗透率计算方法:中国,ZL20181664.X[P]. 2019-10-22. https://www.patent.com.cn.
[本文引用: 1]
ZENG F H, PENG F, GUO J C, et al. A Calculation Method for Permeability of Complex Fracture Network:China,ZL20181664.X[P].2019-10-22. https://www.patent.com.cn.
[本文引用: 1]
[18]
秦积舜, 李爱芬. 油层物理学[M]. 北京: 石油大学出版社, 2003.
[本文引用: 2]
QIN J S, LI A F. Reservoir Physics[M]. Beijing: Petroleum University Press, 2003.
[本文引用: 2]
[19]
ZENG F, PENG F, GUO J. Gas mass transport model for microfractures considering the dynamic variation of width in shale reservoirs[J].SPE Reservoir Evaluation & Engineering,2019, 22(4): 1265-1281.
[本文引用: 1]
[20]
LI Y, DONG P, ZHOU D, et al. Research on dynamic model of micro-fracture apparent permeability in shale gas reservoir [J]. Rock and Soil Mechanics, 2018, 39(1): 51-59.
[21]
LI Y, DONG P, ZHOU D. A dynamic apparent permeability model for shale microfractures: Coupling poromechanics, fluid dynamics, and sorption-induced strain[J]. Journal of Natural Gas Science and Engineering, 2020, 74: 103104.
[本文引用: 3]
[22]
WU K, LI X, CHEN Z, et al. Gas transport behavior through micro fractures of shale and tight gas reservoirs[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(6): 955-964.
[本文引用: 1]
[23]
WANG S F, YU B M, ZHENG Q, et al. A fractal model for the TPG for Bingham fluids in porous media embedded with randomly distributed fractal-like tree networks[J]. Advances in Water Resources, 2011, 34(12): 1574-1580.
[本文引用: 1]
[24]
RAHMAN M K, HOSSIAN M. A shear-dilation-based model for evaluation of hydraulically stimulated naturally fractured reservoirs[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002,26(5): 469-497.
[本文引用: 1]
[25]
朱维耀, 马东旭, 亓倩, 等. 复杂缝网页岩压裂水平井多区耦合产能分析[J]. 天然气工业, 2017, 37(7): 60-68.
[本文引用: 1]
ZHU W Y, MA D X, QI Q, et al. Multi-zone coupling productivity of horizontal well fracturing with complex fracture networks in shale gas reservoirs[J].Natural Gas Industry, 2017, 37(7): 60-68.
[本文引用: 1]
[26]
FINK R, KROOSS A B M, GENSTERBLUM Y, et al. Apparent permeability of gas shales-superposition of fluid dynamic and poro-elastic effects[J]. Fuel, 2017,199(1):532-550.
[本文引用: 1]
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
2
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
... 深层页岩气藏体积压裂改造后近主裂缝面处的裂缝网络分布十分复杂,会形成一个非均质的缝网改造区[5 ] ,页岩气的渗流机理也因为缝网区的非均质分布变得很复杂,合理并准确的描述裂缝网络变得十分重要.由于实际缝网改造区的岩心不易获得,所以用人工造缝岩心代替SRV 区域的真实结构,通过CT扫描并在此基础上确定裂缝条数、裂缝位置、裂缝的几何参数(倾角、宽度、裂缝位置等),运用蒙特卡洛随机建模方法生成随机裂缝网络,通过对缝网裂缝二值化处理,最后生成裂缝网络[2 ,17 ] .对于得到的离散二维裂缝网络,基于流量等效原理[18 ] ,在直角坐标系中对其进行正交分解,得到x 方向和y 方向的两簇平行裂缝,裂缝的长度变化范围远小于宽度变化,为了简便计算,可对裂缝长度取平均值,分解过程如图1 所示: ...
2
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
... 深层页岩气藏体积压裂改造后近主裂缝面处的裂缝网络分布十分复杂,会形成一个非均质的缝网改造区[5 ] ,页岩气的渗流机理也因为缝网区的非均质分布变得很复杂,合理并准确的描述裂缝网络变得十分重要.由于实际缝网改造区的岩心不易获得,所以用人工造缝岩心代替SRV 区域的真实结构,通过CT扫描并在此基础上确定裂缝条数、裂缝位置、裂缝的几何参数(倾角、宽度、裂缝位置等),运用蒙特卡洛随机建模方法生成随机裂缝网络,通过对缝网裂缝二值化处理,最后生成裂缝网络[2 ,17 ] .对于得到的离散二维裂缝网络,基于流量等效原理[18 ] ,在直角坐标系中对其进行正交分解,得到x 方向和y 方向的两簇平行裂缝,裂缝的长度变化范围远小于宽度变化,为了简便计算,可对裂缝长度取平均值,分解过程如图1 所示: ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
2
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
... 深层页岩气藏体积压裂改造后近主裂缝面处的裂缝网络分布十分复杂,会形成一个非均质的缝网改造区[5 ] ,页岩气的渗流机理也因为缝网区的非均质分布变得很复杂,合理并准确的描述裂缝网络变得十分重要.由于实际缝网改造区的岩心不易获得,所以用人工造缝岩心代替SRV 区域的真实结构,通过CT扫描并在此基础上确定裂缝条数、裂缝位置、裂缝的几何参数(倾角、宽度、裂缝位置等),运用蒙特卡洛随机建模方法生成随机裂缝网络,通过对缝网裂缝二值化处理,最后生成裂缝网络[2 ,17 ] .对于得到的离散二维裂缝网络,基于流量等效原理[18 ] ,在直角坐标系中对其进行正交分解,得到x 方向和y 方向的两簇平行裂缝,裂缝的长度变化范围远小于宽度变化,为了简便计算,可对裂缝长度取平均值,分解过程如图1 所示: ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
2
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
... 基于储层裂缝具有高度的自相似性,通过分形理论对单裂缝进行尺度升级,从微观单裂缝求和得到宏观裂缝网络的总流量方程[12 ] . ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
1
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
2
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
... 为了研究深层页岩气在复杂缝网中的渗流机理,本文基于流量等效原理将二维复杂缝网正交分解为x 、y 方向的平行裂缝簇.从单裂缝出发,考虑地应力变化对缝宽变化的影响[16 ] ,通过页岩气的黏性流、克努森扩散、表面扩散建立单缝流量方程.通过分形理论将尺度升级到平行裂缝簇,耦合得到缝宽动态变化下的缝网渗透率计算模型. ...
2
... 体积压裂是实现深层页岩气开发的关键手段.体积压裂形成的缝网结构和页岩气在缝网中的渗流机理是决定其导流能力的关键因素.目前预测复杂缝网渗透率的研究方法主要有双重介质模型和离散裂缝网络模型[1 ] .王晨星[2 ] 采用蒙特卡洛随机建模方法,基于缝网真实特征建立了二维平面离散裂缝网络模型;ROBERTSON等[3 ] 基于弹性力学理论,并用立方网格描述储层缝网;也有研究[4 -5 ] 通过微地震数据反演和DFN方法来描述缝网形态;王文东[6 ] 基于随机分形树状网络,通过微地震反演得到缝网的几何分布.针对页岩气在裂缝中的渗流机理方面,曲鸿雁等[7 ] 基于多孔弹性理论,考虑页岩吸附变形的特点建立了页岩裂缝表观渗透率模型,但忽略了页岩气的不同传输机理;吴克柳等[8 ] 通过耦合黏性流和滑脱流传输机理建立了页岩储层微裂缝表观渗透率计算模型,但未考虑应力敏感效应导致的缝宽动态变化;曾凡辉等[9 ] 运用弹塑性力学、解吸附理论,进一步考虑页岩气在微裂缝中不同流动机理,建立了考虑页岩微裂缝缝宽动态变化的渗透率模型,但该模型只能用于计算单裂缝;因为页岩压裂后储层各类孔隙形状、大小以及分布具有自相似性[10 ] ;MAHAMUD等[11 ] 通过CT成像、压汞以及 N2 吸附计算得到的分形维数定量描述了页岩多孔介质的不规则孔隙结构, XIE等[12 ] 应用分形与多重分形技术,定量描述了孔隙大小分布、非均质性及其复杂程度,进而定量描述孔隙特征,LI等[13 ] 通过二维SEM图像获取了不同尺度孔隙特征,进一步通过典型特征单元确定了研究区域大小;在此基础上,针对缝网结构的复杂性,YU等[14 ] 和LI等[15 ] 利用树状分形理论建立裂缝网络的渗透率模型;李玉丹等[16 ] 通过分形理论对单一裂缝进行尺度升级,建立了简单二维平行缝网的渗透率模型,但该模型对气体在不同尺度裂缝中的滑脱流、克努森流和表面扩散等流动机理考虑不够全面. ...
... 为了研究深层页岩气在复杂缝网中的渗流机理,本文基于流量等效原理将二维复杂缝网正交分解为x 、y 方向的平行裂缝簇.从单裂缝出发,考虑地应力变化对缝宽变化的影响[16 ] ,通过页岩气的黏性流、克努森扩散、表面扩散建立单缝流量方程.通过分形理论将尺度升级到平行裂缝簇,耦合得到缝宽动态变化下的缝网渗透率计算模型. ...
1
... 深层页岩气藏体积压裂改造后近主裂缝面处的裂缝网络分布十分复杂,会形成一个非均质的缝网改造区[5 ] ,页岩气的渗流机理也因为缝网区的非均质分布变得很复杂,合理并准确的描述裂缝网络变得十分重要.由于实际缝网改造区的岩心不易获得,所以用人工造缝岩心代替SRV 区域的真实结构,通过CT扫描并在此基础上确定裂缝条数、裂缝位置、裂缝的几何参数(倾角、宽度、裂缝位置等),运用蒙特卡洛随机建模方法生成随机裂缝网络,通过对缝网裂缝二值化处理,最后生成裂缝网络[2 ,17 ] .对于得到的离散二维裂缝网络,基于流量等效原理[18 ] ,在直角坐标系中对其进行正交分解,得到x 方向和y 方向的两簇平行裂缝,裂缝的长度变化范围远小于宽度变化,为了简便计算,可对裂缝长度取平均值,分解过程如图1 所示: ...
1
... 深层页岩气藏体积压裂改造后近主裂缝面处的裂缝网络分布十分复杂,会形成一个非均质的缝网改造区[5 ] ,页岩气的渗流机理也因为缝网区的非均质分布变得很复杂,合理并准确的描述裂缝网络变得十分重要.由于实际缝网改造区的岩心不易获得,所以用人工造缝岩心代替SRV 区域的真实结构,通过CT扫描并在此基础上确定裂缝条数、裂缝位置、裂缝的几何参数(倾角、宽度、裂缝位置等),运用蒙特卡洛随机建模方法生成随机裂缝网络,通过对缝网裂缝二值化处理,最后生成裂缝网络[2 ,17 ] .对于得到的离散二维裂缝网络,基于流量等效原理[18 ] ,在直角坐标系中对其进行正交分解,得到x 方向和y 方向的两簇平行裂缝,裂缝的长度变化范围远小于宽度变化,为了简便计算,可对裂缝长度取平均值,分解过程如图1 所示: ...
2
... 深层页岩气藏体积压裂改造后近主裂缝面处的裂缝网络分布十分复杂,会形成一个非均质的缝网改造区[5 ] ,页岩气的渗流机理也因为缝网区的非均质分布变得很复杂,合理并准确的描述裂缝网络变得十分重要.由于实际缝网改造区的岩心不易获得,所以用人工造缝岩心代替SRV 区域的真实结构,通过CT扫描并在此基础上确定裂缝条数、裂缝位置、裂缝的几何参数(倾角、宽度、裂缝位置等),运用蒙特卡洛随机建模方法生成随机裂缝网络,通过对缝网裂缝二值化处理,最后生成裂缝网络[2 ,17 ] .对于得到的离散二维裂缝网络,基于流量等效原理[18 ] ,在直角坐标系中对其进行正交分解,得到x 方向和y 方向的两簇平行裂缝,裂缝的长度变化范围远小于宽度变化,为了简便计算,可对裂缝长度取平均值,分解过程如图1 所示: ...
... 深层页岩气流动满足广义达西定律[18 ] : ...
2
... 深层页岩气藏体积压裂改造后近主裂缝面处的裂缝网络分布十分复杂,会形成一个非均质的缝网改造区[5 ] ,页岩气的渗流机理也因为缝网区的非均质分布变得很复杂,合理并准确的描述裂缝网络变得十分重要.由于实际缝网改造区的岩心不易获得,所以用人工造缝岩心代替SRV 区域的真实结构,通过CT扫描并在此基础上确定裂缝条数、裂缝位置、裂缝的几何参数(倾角、宽度、裂缝位置等),运用蒙特卡洛随机建模方法生成随机裂缝网络,通过对缝网裂缝二值化处理,最后生成裂缝网络[2 ,17 ] .对于得到的离散二维裂缝网络,基于流量等效原理[18 ] ,在直角坐标系中对其进行正交分解,得到x 方向和y 方向的两簇平行裂缝,裂缝的长度变化范围远小于宽度变化,为了简便计算,可对裂缝长度取平均值,分解过程如图1 所示: ...
... 深层页岩气流动满足广义达西定律[18 ] : ...
1
... 地应力变化引起的缝宽变化由裂缝压缩性、基质压缩性、气体解吸附性三部分共同作用产生,所以由压力变化导致的页岩裂缝宽度总变化量为[19 -21 ] : ...
3
... 地应力变化引起的缝宽变化由裂缝压缩性、基质压缩性、气体解吸附性三部分共同作用产生,所以由压力变化导致的页岩裂缝宽度总变化量为[19 -21 ] : ...
... LI等[21 ] 同样考虑应力敏感引起的动态缝宽变化,建立了简单平行多裂缝的渗透率模型,而基于本文模型建立的复杂缝网的等效处理方法,并进一步耦合页岩气在缝网中的多种流动机理得到一个更为全面的复杂缝网渗透率动态表征模型.为了充分说明本文模型的准确性和适用性,将本文计算模型与LI等[21 ] 简单缝网渗透率模型和FINK等[26 ] 实验数据进行对比验证,对比结果如图2 所示. ...
... [21 ]简单缝网渗透率模型和FINK等[26 ] 实验数据进行对比验证,对比结果如图2 所示. ...
1
... 根据分形理论,缝网中的裂缝宽度大于等于b 的裂缝条数表示为[22 ] : ...
1
... 对于矩形裂缝,同时考虑孔隙度对裂缝截面积的影响,分形截面积A p [23 ] : ...
1
... 对于x 方向和y 方向的2簇平行裂缝,分别将b x m a x b x m i n a x ¯ b y m a x b y m i n a y ¯ 式(14) —式(24) ,可以得到2个方向各自的渗透率K x K y [24 ] : ...
1
... 朱维耀等[25 ] 曾选取龙马溪组页岩岩样,采用巴西劈裂法进行人工造缝,利用覆压孔渗仪对压裂前后的渗透率进行测量,此处以本文模型计算结果与其进行对比验证,岩样基本参数如表2 所示. ...
1
... 朱维耀等[25 ] 曾选取龙马溪组页岩岩样,采用巴西劈裂法进行人工造缝,利用覆压孔渗仪对压裂前后的渗透率进行测量,此处以本文模型计算结果与其进行对比验证,岩样基本参数如表2 所示. ...
1
... LI等[21 ] 同样考虑应力敏感引起的动态缝宽变化,建立了简单平行多裂缝的渗透率模型,而基于本文模型建立的复杂缝网的等效处理方法,并进一步耦合页岩气在缝网中的多种流动机理得到一个更为全面的复杂缝网渗透率动态表征模型.为了充分说明本文模型的准确性和适用性,将本文计算模型与LI等[21 ] 简单缝网渗透率模型和FINK等[26 ] 实验数据进行对比验证,对比结果如图2 所示. ...





 甘公网安备 62010202000678号
甘公网安备 62010202000678号