水力压裂条件下裂隙性煤储层垂直试验井产能预测

doi:10.11764/j.issn.1672-1926.2020.10.006

水力压裂条件下裂隙性煤储层垂直试验井产能预测

王志荣^,, 温震洋, 陈玲霞

郑州大学水利科学与工程学院，河南郑州 450001

Productivity prediction of vertical test well for fractured coal reservoir under hydraulic fracturing

WANG Zhi-rong^,, WEN Zhen-yang, CHEN Ling-xia

School of Hydraulic Science and Engineering，Zhengzhou University，Zhengzhou 450001，China

收稿日期: 2020-08-28 修回日期: 2020-09-28 网络出版日期: 2021-04-09

基金资助:

国家自然科学基金项目. 41272339
河南省自然科学基金项目. 182300410149

Received: 2020-08-28 Revised: 2020-09-28 Online: 2021-04-09

作者简介 About authors

王志荣（1963-），男，浙江嘉善人，教授，博士，主要从事地质工程与地质灾害防治研究.E-mail：wangzhirong513@sina.com. , E-mail：wangzhirong513@sina.com

摘要

煤层气井产能预测一直是天然气工业领域试图解决的技术性难题。为探究水力压裂条件下裂隙性煤储层气渗透机理及产能规律，首先考虑其原生裂隙的几何特征对裂缝扩展规律的影响，结合经典PKN模型建立了改进的水力裂缝扩展模型；其次考虑排采过程中水力裂缝几何尺寸变化对煤储层孔隙率的影响，基于储层压力梯度动态方程建立了储层动态渗透率模型；最后运用流体质量守恒原理建立了裂隙性储层煤层气垂直井产能预测模型。运用该模型对河南焦作“三软”矿区GW试⁃008井进行了试验期70 d的产能计算，并与实际排采值进行对比，发现理论计算值与实际排采值动态变化曲线吻合度较高，平均日产气量分别为360.768 m³/d与381.489 m³/d，相对误差仅为6%，验证了产能模型的正确性。研究成果对我国“三软”矿区煤层气的开发利用具有重要的借鉴意义。

关键词： 原生裂隙 ; 水力裂缝 ; 动态渗透率 ; 产能模型

Abstract

Production capacity prediction of CBM is a difficult technical problem that the natural gas industry tries to solve. In order to explore the permeability mechanism and productivity rule of fractured CBM reservoirs in the "three soft" coking mining area under the condition of hydraulic fracturing， firstly， the influence of geometric characteristics of primary fractures on fracture growth rule was considered， and an improved hydraulic fracture growth model was established in combination with the classical PKN model； secondly， a reservoir dynamic permeability model was established based on the dynamic equation of reservoir pressure gradient， considering the influence of the geometric size change of hydraulic fractures on the porosity of primary fractures in coal during drainage and production； finally， based on the principle of fluid mass conservation， the productivity prediction model of CBM vertical wells in fractured reservoirs was established. This model was used to calculate the production capacity of Well GW-008 during the trial period of 70 days in the mining area， and it was compared with the actual discharge and production value. It was founded that the dynamic change curve of the theoretical calculation value and the actual discharge and production value was in good agreement with each other. The average daily gas output is 360.768 m³/d and 381.489 m³/d respectively， and the relative error is only 6%， thus verifying the correctness of the production capacity model. The research results are of great significance to the development and utilization of coalbed methane in the “three soft” areas of China.

Keywords： Native fissure ; Hydraulic fracturing ; Dynamic permeability ; Productivity model

PDF (1304KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王志荣, 温震洋, 陈玲霞. 水力压裂条件下裂隙性煤储层垂直试验井产能预测. 天然气地球科学[J], 2021, 32(4): 465-471 doi:10.11764/j.issn.1672-1926.2020.10.006

WANG Zhi-rong, WEN Zhen-yang, CHEN Ling-xia. Productivity prediction of vertical test well for fractured coal reservoir under hydraulic fracturing. Natural Gas Geoscience[J], 2021, 32(4): 465-471 doi:10.11764/j.issn.1672-1926.2020.10.006

0 引言

煤层气产能预测是煤层气开采潜力评价的一项指标，对煤层气资源合理开发有着重要的指导意义^［1-2］。河南省作为产煤大省，煤层气资源极为丰富，全省埋深0~2 000 m的煤层气资源总储量超过1×10¹²m³，省内焦作矿区有近百年的煤炭开采历史，经多次矿井勘探与抽采技术评价，已经成为研究煤层气产能预测的理想场所^［3-5］。然而区内煤层存在典型的“三低一高”（低压、低渗、低饱和、高地质变动程度）地质特征，常规油气开采技术难以适用，因而在开发中需对储层进行压裂改造^［6-7］。迄今为止，国内外许多专家学者对煤层气井的产能预测进行了大量研究。岑学齐等^［8］在煤层气理想模型假设的基础上建立了计算产量所需各参数的方程，并结合产量计算方程和静态物质平衡方程推导出产能预测解析模型；吴静^［9］利用CBM-SIM煤层气数值模拟软件，深入分析了煤层厚度、渗透率、含气量、吸附性、储层压力、含气饱和度和临储比等煤储层因素对煤层气井产能的影响；王保辉等^［10］考虑煤岩面割理和端割理2个方向不同的渗流性质，建立了煤岩割理正交各向异性数学模型，并对鄂尔多斯盆地东部煤层单井产能进行了模拟计算；王琰琛等^［11］基于平行板理论和等值渗流阻力原理，建立了考虑吸附、解吸和扩散特征的煤层气藏连续等效介质模型，并计算分析了煤层气藏压裂直井的IPR曲线；PANTEHA等^［12］考虑储层几何形状、煤层气井底压力和流体速度等因素，提出了预测煤层气产能的方法；郭肖等^［13］基于煤岩双孔单渗模型、砂岩单孔单渗模型和煤岩与砂岩层间窜流模型，构建了煤层气与砂岩气合采的数值模型，并对影响合采产能和层间窜流强度的因素进行了敏感性分析。

目前国内外对煤层气井产能预测进行了广泛研究，但大多数将煤储层简化为单一均质储层，且尚未考虑原生裂隙和水力裂缝耦合作用对煤层气解析渗流产出的影响，因而无法对裂隙性储层产能进行准确分析预测。鉴于此，本文基于弹性力学、断裂力学与流体力学等基本理论，考虑开采过程中储层原生裂隙和水力裂缝之间的相互作用，建立了储层动态渗透率模型，并依据流体能量守恒原理建立了煤层气垂直井产能预测模型。运用该模型对焦作矿区GW试-008井进行应用分析，从而验证了该模型的正确性。研究成果对我国“三软”矿区煤层气开发利用具有重要的借鉴意义。

1 储层渗透模型

在煤层气井进行抽放或排采时，垂直井井筒附近储层会形成压降漏斗，使得煤颗粒表面的煤层气由吸附态转变为游离态，从而通过原生裂隙扩散进入水力裂缝，再经由水力裂缝渗流到井筒。因此探究煤储层渗透率随开采时间的变化规律是进行煤层气产能预测的关键。

1.1　起裂压力模型

煤体在成岩与改造过程中，在自重应力与构造应力的作用下会导致岩体内部形成大量的原生裂隙。由文献［14］可知储层原生裂隙的间距、宽度和密度对水力裂缝起裂与延伸有着重要影响，因此要想准确反映水力裂缝扩展延伸规律，必须考虑储层基于原生裂隙几何特征的起裂压力。由于原生裂隙强度问题已经不符合材料力学研究范围，而断裂力学的强度理论恰能够解决裂隙性煤岩体的破裂问题，此时含有原生裂隙几何特征参数的垂直井起裂压力模型可表示为：

\begin{array}{l} P_{s} = \frac{2 γ α K^{2} K_{I C}}{4.6 g R_{w}^{3} \sqrt[]{a π} (6.569 - L n R_{w}^{2})} + \\ 2 γ R_{w} + σ_{H} \end{array}

（1）

式中：P_s为起裂压力，MPa；γ为煤岩体重度，kN/m³；α为动能修正系数，无量纲；K为煤储层等效渗透系数，m/d；K_IC为煤岩体的断裂韧性常数，MPa·m^0.5；R_w为井筒半径，m；a为复合型裂隙半长，m；σ_H为煤储层最大水平主应力，MPa。

对于较为发育的裂隙性储层，基于岩石力学基本理论，其渗透特性参数可表示为：

\{\begin{array}{l} K = k_{0} \frac{ρ g}{η_{b}} \\ k_{0} = b^{3} λ S^{- 1} \end{array}

（2）

式中：k₀为储层初始渗透率，μm²；ρ为压裂液体密度，kg/m³；g为重力加速度，m/s²；η_b为煤层气黏度，MPa·s；b、S分别为原生裂隙的平均宽度与间距，mm；λ与原生裂隙面粗糙度有关的系数，无量纲。

将式（1）的变量进行组合定义：

\{\begin{array}{l} I = \frac{α K^{2} K_{I C}}{g \sqrt[]{a π}} \\ R_{μ} = 4.6 R_{w}^{3} (6.569 - L n R_{w}^{2}) \end{array}

（3）

则可得出裂隙性储层煤层气垂直井起裂压力计算公式：

P_{s} = 2 γ \frac{I}{R_{μ}} + 2 γ R_{w} + σ_{H}

（4）

基于损伤力学与等效应变假设，煤岩体发生破裂后，其强度发生弱化。此时控制裂缝延伸的压力折减为起裂压力的（1－D）倍：

P_{y s} = (1 - D) (2 γ \frac{I}{R_{μ}} + 2 γ R_{w} + σ_{H})

（5）

式中：P_ys为延伸压力，MPa。

1.2　水力裂缝扩展模型

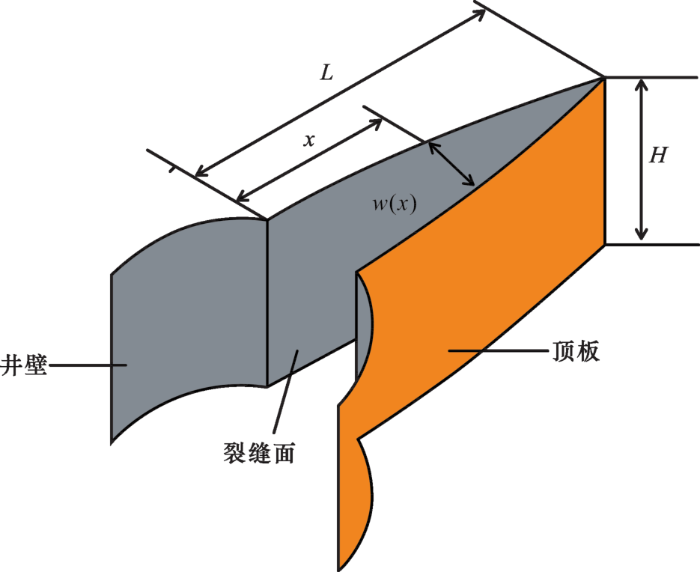
由于研究区压裂缝的长宽比远大于1，故可采用经典的PKN模型来描述裂缝的扩展延伸过程。假设压裂产生的垂直裂缝高度等于煤层厚度，煤岩变形服从应力应变关系，水平切面为平面应变，并在压裂完成后简化为椭圆形，裂缝扩展模型如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 裂缝扩展模型

Fig. 1 Fracture propagation model

在注水压裂阶段，前置液和携砂液的作用分别为造缝和撑缝。由流体体积守恒定律可知，注入压裂液总体积应等于撑缝体积加滤失体积，即：

Q_{F} (t) + Q_{L} (t) = q t

（6）

式中：Q_F（t）为t时刻用于撑缝的压裂液体积，m³；Q_L（t）为t时刻滤失到地层中的压裂液体积，m³；q为压裂液排量，m³/min；t为压裂液注入时间，min。

当压裂液充满水力裂缝时，用于撑缝的压裂液体积应等于水力裂缝体积，即：

Q_{F} (t) = 2 \int_{0}^{L} H W (x) d x

（7）

式中：L为单翼裂缝长度，m；H为裂缝高度，m；W（x）为裂缝延伸方向上距井壁x处裂缝宽度，m。

水力裂缝某一断面上的裂缝宽度W（x）与该断面上净压力ΔP的关系为：

W (x) = \frac{(1 - 2 μ) H}{G} Δ P

（8）

式中：μ为煤岩泊松比，无量纲；G为煤岩的剪切模量，Pa；ΔP为裂缝断面处净压力，Pa。

对上式求x的偏导可得：

\{\begin{array}{l} \frac{\partial W}{\partial x} = \frac{(1 - 2 μ) H}{G} \frac{\partial P}{\partial x} \\ \frac{\partial P}{\partial x} = - Δ P \end{array}

（9）

水力裂缝在延伸过程中，筒侧壁破裂应力P_i折减为延伸应力P_ys，结合张小东等^［15］对煤层水力裂缝在延伸过程中应力状态以及其压降衰减规律的研究可知，距井壁x处的裂缝内净压力关于位置x变化的关系式可表示为：

Δ P (x) = (P_{y s} - \frac{μ}{1 - μ} P_{e}) \sqrt[]{1 - {(\frac{x}{L})}^{2}}

（10）

式中：P_e为原始储层应力，MPa；x为裂缝断面距离井筒侧壁长度，m。

当裂缝延伸到水力裂缝末端时，W=0，联立式（9）和式（10），得：

W (x) = \frac{(2 μ - 1) H}{G} (P_{y s} - \frac{μ}{1 - μ} P_{e}) [L a r c s i n (\frac{x}{L}) - \frac{x^{3}}{L^{2}} + x]

（11）

联立式（7）和式（11），并对x进行积分，得：

Q_{F} (t) = \frac{(1 - μ) π}{4 G} (P_{y s} - \frac{μ}{1 - μ} P_{e}) L H^{2}

（12）

由文献［15］可知，滤失到地层中的压裂液体积可表示为：

Q_{L} (t) = 4 \int_{0}^{L} \int_{0}^{t} \frac{C H}{\sqrt[]{t_{0} - τ}} d τ d x

（13）

式中：C为压裂液滤失系数，m/min^0.5；t₀为压裂施工总时间，min； $τ$ 为压裂液到达该位置处的时间，min。

对式（13）进行积分，可得：

Q_{L} (t) \approx 8 C H L \sqrt[]{t}

（14）

将式（12）和式（14）代入式（6）并简化整理可得水力裂缝长度随压裂时间的变化关系为：

L (t) = \frac{q t}{\frac{(1 - μ) π}{4 G} H^{2} (P_{y s} - \frac{μ}{1 - μ} P_{e}) + 8 C H \sqrt[]{t}}

（15）

由式（2）—式（5）分析可知，裂隙性储层的裂隙粗糙度、宽度和平均间距等对水力裂缝扩展延伸有着重要的影响，原生裂隙粗糙度与宽度越小，平均间距越大，则延伸压力越小。再由式（11）和式（15）可知延伸压力越小，则在相同压裂时间内水力裂缝几何尺寸越大。因而在实际压裂过程中必须要考虑煤储层原生裂隙的几何特征参数对延伸压力的作用，从而控制水力裂缝扩展延伸的几何尺寸，为产能计算奠定基础。

1.3　渗透率动态模型

在煤层气井排采阶段，随着吸附在煤颗粒表面的煤层气不断解析，储层中气体压力随之降低，但上覆地层压力不变，必然会导致煤骨架所受压应力增大。由于煤层具有可压缩性，煤层骨架压力的增加会促使水力裂缝和原生裂隙几何尺寸发生变化，从而导致储层渗透率发生动态变化。因此，在排采阶段，必须考虑煤岩储层压力的压降对水力裂缝和原生裂隙几何尺寸的作用。

根据于本福等^［16］对储层压力分布的研究，储层压力动态变化的数学物理方程为：

\{\begin{array}{l} \frac{\partial^{2} P (r, t)}{\partial^{2} r} + \frac{1}{r} \frac{\partial P (r, t)}{\partial r} = \frac{1}{η} \frac{\partial P (r, t)}{\partial t} \\ {P (r, t)|}_{t = 0} = P_{e} \\ {\frac{\partial P (r, t)}{\partial r}|}_{r = r_{w}} = \frac{G_{g} μ}{2 π k_{0} r_{w}} \end{array}

（16）

式中：P（r，t）为储层应力函数，Pa；P_e为初始储层压力，MPa；r为应力影响区域半径，m；η为导压系数，m²/s；G_g为气体重力流量，N/s；t为抽采时间，d。

假设煤储层为水平无限大地层，距井筒无穷远处储层压力不变，则垂直井应力边界条件可表示为：

P (r, t) |_{r = \infty} = P_{e}

（17）

联立式（16）和式（17）可得储层应力与煤层气抽采时间和应力影响区域半径r之间的关系：

\{\begin{array}{l} P (r, t) = \sqrt[]{{P_{e}}^{2} + \frac{q_{s c} μ}{2 π k_{0} h η} e^{- \frac{r^{2}}{4 x t}}} \\ η = \frac{T_{s c} G_{g}}{P_{s c} \bar{Z T}} \end{array}

（18）

将式（18）带入式（9）即可得水力裂缝内净压力随抽采时间的变化关系：

Δ P (x, t) = (P_{y s} - \frac{μ}{1 - μ} \sqrt[]{{P_{e}}^{2} + \frac{q_{s c} μ}{2 π k_{0} h η} e^{- \frac{r^{2}}{4 x t}}}) \sqrt[]{1 - {(\frac{x}{L})}^{2}}

（19）

式中：T_sc为标准状况温度，K；T为煤岩储层温度，K；q_sc为平均日产气量，m³/d；P_sc为标况下的大气压，MPa。

联立式（11）和式（19）即可得水力裂缝宽度随抽采时间的变化关系：

\{\begin{array}{l} W (x, t) = ϑ L [P_{y s} - \frac{μ}{1 - μ} \sqrt[]{{P_{e}}^{2} + \frac{q_{s c} μ}{2 π k_{0} h η} e^{- \frac{r^{2}}{4 x t}}}] \\ ϑ = \frac{(1 - 2 μ) H}{G} [L a r c s i n (\frac{x}{L}) - \frac{x^{3}}{L^{2}} + x] \end{array}

（20）

联立式（15）和式（19）可得水力裂缝长度随抽采时间的变化关系：

L (x, t) = \frac{G L q t}{0.79 H^{2} [P_{y s} (1 - μ) - μ \sqrt[]{{P_{e}}^{2} + \frac{q_{s c} μ}{2 π k_{0} h η} e^{- \frac{r^{2}}{4 x t}}}] \sqrt[]{L^{2} - x^{2}} + 8 G C H \sqrt[]{t}}

（21）

单裂缝储层的煤岩体孔隙率为：

ϕ (x, t) = \frac{2 W}{π L} (1 - S_{c})

（22）

式中： $ϕ (x, t)$ 为煤岩体孔隙率，无因次；S_c为缝内砂比，无因次。

考虑煤岩体孔隙率对其渗透率的影响，渗透率计算公式可表示为：

k (x, t) = 8.33 \times 10^{6} W^{2} \times φ

（23）

式（23）中：k（x，t）为压裂后的渗透率，μm²。

联立式（20）—式（23），可得煤层气抽采过程中储层动态渗透率计算模型：

\begin{array}{l} k (x, t) = 4.2 \times 10^{6} ϑ^{3} (1 - S_{c}) \times \\ \frac{H^{2} L^{3} Δ P^{4} (1 - μ) + 10.13 G C H L^{3} \sqrt[]{t} Δ P^{3}}{G q t} \end{array}

（24）

2 产能预测模型

在排采阶段，假设煤层气在压裂缝端部为径向流，在中部为单向流，则垂直井煤层气总产能计算公式可表示为^［17］：

Q = (4 L + 2 π) k h ρ_{m} \int_{0}^{r_{0}} (V_{m} - \frac{V_{L}^{} P_{t}}{P_{L} + P_{t}}) r d r

（25）

式中：ρ_m为研究区煤层气资源丰度，m³/km²；V_L为Langmuir体积，cm³/g；V_m为煤层气含量，m³/t；P_L为Langmuir压力，MPa；P_t为边界压力，MPa；r₀为水力裂缝半长。

由于研究区煤层倾角较小，因此可认为煤层初始储层压力在垂直井影响范围内是恒定的^［18］。边界压力可表示为：

P (r, t) = P_{e}

（26）

对上式积分得：

Q = (2 L + π) V_{m} k h {r_{0}}^{2} ρ_{m} [1 - \frac{V_{L} P_{e}}{(p_{L} + p_{e}) V_{m}}]

（27）

将式（5）、式（15）和式（24）代入式（27），令：

\{\begin{array}{l} β = \frac{4.2 \times 10^{6} ϑ^{3} (1 - S_{c}) (2 L + π) ρ_{m} V_{m} h {r_{0}}^{2} [(P_{L} + P_{e}) V_{m} - V_{L} P_{e}]}{(P_{L} + P_{e}) L V_{m}} \\ N_{1} = (1 - μ) H^{2} (P_{y s} {- \frac{μ}{1 - μ} \sqrt[]{P_{e}^{2} + \frac{q_{s c} μ}{2 π k_{0} h η} e^{- \frac{r^{2}}{4 x t}}})}^{4} (L^{2} - x^{2})^{2} \\ N_{2} = 10.13 G C H L \sqrt[]{t} (P_{y s} {- \frac{μ}{1 - μ} \sqrt[]{P_{e}^{2} + \frac{q_{s c} μ}{2 π k_{0} h η} e^{- \frac{r^{2}}{4 x t}}})}^{3} (L^{2} - x^{2})^{3 / 2} \end{array}

(28)

则可得产能预测模型：

Q = \frac{β (N_{1} + N_{2})}{G q t}

（29）

3 实例验证

3.1　研究区概况

焦作九里山矿区位于华北板块板内太行山隆起东南侧与华北沉降带结合部斜坡带西缘，主要含煤地层为石炭系上统太原组和二叠系下统山西组。山西组二₁煤层为矿区主采煤层，裂隙较为发育，层位稳定，结构简单，总体为向ES倾斜的单斜构造，地层产状为120°∠12°~120°∠16°。煤层埋深多处为155~800 m，有效埋深为50~700 m，十分有利于煤层气的开发。煤顶板以致密砂岩与砂质泥岩为主，岩石完整，裂隙不发育，岩石渗透率为（2.5~4.2）×10^-17 m²，渗透性较差，隔水性良好，是一层较好的气盖层。煤层底板多为泥岩与炭质泥岩，裂隙不发育，岩石渗透率约为2.8×10^-17 m²，渗透性较差，隔水性良好。煤层顶底板特性保证了煤层气被圈闭在煤层中以原地吸附的形式保存，十分有利于煤层气的储集。

3.2　渗透率计算

GW试-008井位于九里山矿区西部，试验井完井深度为590 m，井筒半径为140 mm，由现场资料可知，煤储层最大水平主应力为11.29 MPa，储层压力为7.7 MPa，弹性模量为2.5 GPa，煤层损伤系数为0.19，泊松比为0.32，压裂液滤失系数为8.30×10^-3m/min^0.5，煤层气黏度为1×10^-5Pa·s。矿井于2008年5月11日进行压裂抽采试验，抽采过程中采用石英砂做支撑剂，活性水做压裂液（表1），并在2008年7月21日抽采结束，累计70 d。抽采期间，矿井最大日产水量为4.10 m³，累计产水量达256.28 m³；最大日产气量为600.08 m³，累计产气量达2.56×10⁴m³，煤层气开采效果良好。

表1 GW试-008井压裂施工参数

Table 1 Fracturing parameters of Well GW test-008

参数		数值
煤层深度/m		583.50
煤层厚度/m		7.01
施工排量/（m³/min）		7.60
时间/min		50
压裂液/m³	前置液	200.00
	携砂液	204.00
	替置液	5.80
	压裂液总量	409.80
平均砂比/%		18.20
施工压力/MPa	破裂压力	9.80
施工压力/MPa	停泵压力	6.60

新窗口打开| 下载CSV

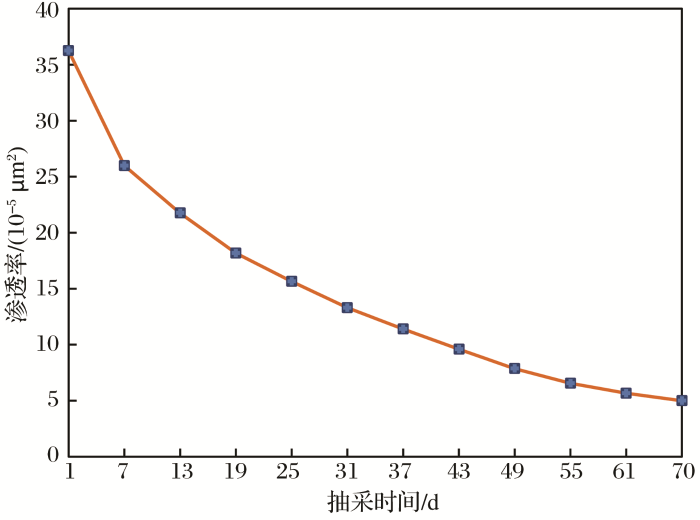
焦作矿区构造简单，总体为一倾向南东、倾角为80°~150°的单斜构造，区域上为多组断层切割形成掀斜式断块构造。EC试-1井构造位置处于矿区断块构造的中心部位，于下二叠统山西组主采二₁煤层中通过钻机采取煤心，因此采样具有一定的代表性。经测试统计煤岩中的169条原生裂隙，可知煤岩体微观裂隙较为发育，主割理密度为1.21~8.20条/cm，长0.01~5.10 cm，高0.01~3.49 cm，裂隙宽度为5~400 mm；次裂隙密度为0.6~3.2条/cm，长0.01~0.8 cm，高0.01~1.90 cm，裂隙宽度为4~300 μm。经分析得出煤储层原生裂隙几何特征参数分别为：裂隙平均长度为0.025 m，平均宽度为3.0×10^-4m，平均间距为2.17×10^-3m。根据室内实验可知：裂隙面粗糙度为0.083，断裂韧性常数为0.295 MPa·m^1/2。将相关施工参数以及煤岩物性参数分别代入水力裂缝扩展模型可得：裂缝延伸压力为13.26 MPa，长度为99.57 m，宽度为20.38 m，再结合渗透率模型即可得出煤储层渗透率随抽采时间的动态变化关系（图2）。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 GW试-008井渗透率动态变化曲线

Fig.2 Dynamic change curve of permeability of Well GW test-008

3.3　产能计算与分析

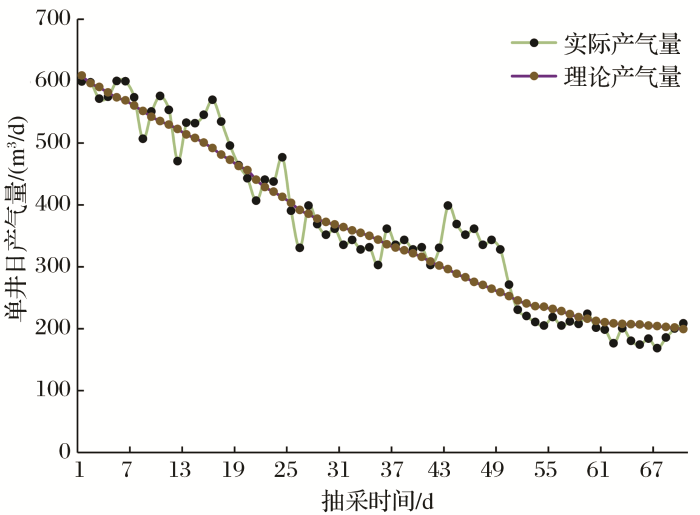
由研究区实测资料可知，区内煤层气资源丰度为1.5×10⁸m³/km²，Langmuir压力均值为2.6 MPa，空气干燥基的Langmuir体积参数为36.1 cm³/g。结合前文计算得出的煤层动态渗透率以及其他参数，将相关参数代入式（28）和式（29）即可求出GW试-008井的理论产气量，并GW试-008井的产气量理论值与实测值对比图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 GW试-008井产气量实测值与理论值对比

Fig.3 Comparison of measured and theoretical gas production values of Well GW test -008

由图3分析可知，压裂结束时，水力裂缝几何尺寸达到最大，此时储层渗透率最大，导致日产气量最大；随着抽采的进行，水力裂缝内净压力不断减小，引起水力裂缝几何尺寸发生变化，使得煤层渗透率不断降低，煤层气日产气量随着抽采时间的增加而减小。由该图可知，煤层气日产气量实测值呈现锯齿状而理论值较为平滑，但二者整体变化趋势相似，均随着抽采时间的增加而逐渐下降。由计算可得，实测值与理论值平均日产气量分别为381.489 m³/d与360.768 m³/d，相对误差仅为6%，从而验证了产能预测模型的正确性。

4 结论

（1）针对焦作矿区裂隙性储层低渗难抽采的性质，在水力压裂条件下，考虑储层原生裂隙和水力裂缝耦合作用对裂缝扩展延伸规律的影响，建立了储层起裂与扩展模型；考虑排采阶段煤骨架压应力增加对与原生裂隙和水力裂缝几何尺寸产生影响，进而建立了裂隙性储层动态渗透率模型。

（2）基于建立的动态渗透率模型，结合流体能量守恒定律，最终建立了裂隙性储层产能预测模型。结合GW试-008井现场施工参数与储层物性参数，对该井抽采期（约70 d）产气量进行计算，并与现场实测值进行对比分析，发现理论值与实测值总体变化趋势一致，均随抽采时间的增加而逐渐降低，平均日产气量分别为360.768 m³/d与381.489 m³/d，相对误差仅为6%，从而验证了该模型的正确性，研究成果一定程度上可以指导焦作“三软”矿区裂隙性储层煤层气的开采。

（3）由裂隙性储层产能模型分析可知，储层原生裂隙粗糙度、宽度和平均间距等几何特征参数对煤层气产能有着重要影响。因此，在实际煤层气井开采过程中，可通过原生裂隙的几何特征参数来控制水力裂缝的几何尺寸，进一步得到渗透率随开采时间的变化规律，从而更加科学地预测裂隙性储层的煤层气产量。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李辉，马遵敬，王旭东，等.沁水盆地南部地区砂体与煤层空间叠置特征及其在煤层气和致密气合采开发中的意义［J］.科学技术与工程，2019，19（7）：70-77.

[本文引用: 1]

LI H， MA Z J， WANG X D， et al. Characteristics of spatial superimposition between sandbody and coal seam and its implications to commingling production for coal-bed methane and tight gas in the southern Qinshui Basin［J］. Science Technology and Engineering，2019，19（7）：70-77.

[本文引用: 1]

[2]

王志荣，郭志伟，徐培远，等.九里山煤矿垂直井起裂压力对煤层气产能的影响［J］.水文地质工程地质，2017，44（4）：124-128，159.

[本文引用: 1]

WANG Z R， GUO Z W， XU P Y， et al. Influence of fracturing pressure of vertical well to CBM capacity in Jiulishan coal mine［J］.Hydrogeology & Engineering Geology，2017，44（4）：124-128，159.

[本文引用: 1]

[3]

付江伟，傅雪海，胡晓，等.焦作矿区煤层气开发的水文地质条件分析［J］.中国矿业，2011，20（4）：105-110.

[本文引用: 1]

FU J W， FU X H，HU X， et al. Analysis on hydrogeological condition for coal bed methane exploitation in Jiaozuo coal-mine area［J］.China Mining Magazine，2011，20（4）：105-110.

[本文引用: 1]

[4]

高灶其，刘文波，闫广厚，等.焦作煤田煤层气富集的控制因素［J］.矿产保护与利用，2015（3）：20-24.

GAO Z Q， LIU W B，YAN G H， et al. The controlling factors of coal seam gas enrichment in Jiaozuo Coalfield［J］. Conservation and Utilization of Mineral Resources，2015（3）：20-24.

[5]

李宏欣.焦作九里山井田煤层气赋存特征分析［J］.中州煤炭，2012（9）：4-6，33.

[本文引用: 1]

LI H X， Analysis on CBM occurrence characteristics of Jiulishan Coalfield in Jiaozuo［J］.China Energy and Environmental Protection，2012（9）：4-6，33.

[本文引用: 1]

[6]

孙文洁，王亚伟，李学奎，等.华北型煤田矿井水文地质类型与水害事故分析［J］.煤炭工程，2015，47（6）：103-105.

[本文引用: 1]

SUN W J， WANG Y W， LI X K， et al. Analysis on hydrogeological classification and water inrush accidents in north China coal mines［J］. Coal Engineering，2015，47（6）：103-105.

[本文引用: 1]

[7]

张党育，蒋勤明，高春芳，等.华北型煤田底板岩溶水害区域治理关键技术研究进展［J］.煤炭科学技术，2020，48（6）：31-36.

[本文引用: 1]

ZHANG D Y， JIANG Q M， GAO C F， et al. Study progress on key technologies for regional treatment of karst water damage control in the of North China coalfield［J］. Coal Science and Technology，2020，48（6）：31-36.

[本文引用: 1]

[8]

岑学齐，吴晓东，梁伟，等.煤层气井产能影响因素分析［J］.科学技术与工程，2014，14（4）：201-204，216.

[本文引用: 1]

CEN X Q， WU X D， LIANG W， et al. Analysis of factors affecting productivity of coalbed gas wells［J］. Science Technology and Engineering，2014，14（4）：201-204，216.

[本文引用: 1]

[9]

吴静.焦坪矿区低阶煤储层因素对煤层气井产能的影响及敏感性分析［J］.煤田地质与勘探，2015，43（5）：44-48.

[本文引用: 1]

WU J. Influence of reservoir factors on low-rank coalbed methane well production and sensitivity analysis［J］. Coal Geology & Exploration，2015，43（5）：44-48.

[本文引用: 1]

[10]

王保辉，闫相祯，杨秀娟.基于煤岩割理正交各向异性的煤层气产能预测［J］.科学技术与工程，2017，17（32）：229-232.

[本文引用: 1]

WANG B H， YAN X Z， YANG X J. Production prediction with the consideration of the orthotropic permeability of coal seam［J］. Science Technology and Engineering，2017，17（32）：229-232.

[本文引用: 1]

[11]

王琰琛，陈胜，孙兰兰.煤层气产能预测新模型［J］.天然气与石油，2018，36（4）：92-97.

[本文引用: 1]

WANG Y C， CHEN S， SUN L L. A new model for productivity prediction of coal-bed methane［J］. Natural Gas and Oil，2018，36（4）：92-97.

[本文引用: 1]

[12]

PANTEHA G， MAHMOUD J， EBRAHIM A， et al. A new and simple model for the prediction of horizontal well productivity in gas condensate reservoirs［J］.Fuel，2018，223：431-450.

[本文引用: 1]

[13]

郭肖，汪志明，曾泉树.煤层气/砂岩气混合气藏合采产能预测及排采优化［J］.科学技术与工程，2019，19（17）：162-167.

[本文引用: 1]

GUO X， WANG Z M， ZENG Q S. Production prediction of hybrid gas reservoirs including coal seams and sandstone seams and development optimization［J］. Science Technology and Engineering，2019，19（17）：162-167.

[本文引用: 1]

[14]

王志荣，贺平，郭志伟，等.考虑裂缝特性指标的煤层气“垂直井”起裂压力计算方法［J］.岩土力学，2018，39（S1）：369-377.

[本文引用: 1]

WANG Z R， HE P， GUO Z W， et al. Calculation of initiation pressure of vertical well for coalbed methane considering crack characteristic index［J］.Rock and Soil Mechanics，2018，39（S1）：369-377.

[本文引用: 1]

[15]

张小东，张鹏，刘浩，等.高煤级煤储层水力压裂裂缝扩展模型研究［J］.中国矿业大学学报，2013，42（4）：573-579.

[本文引用: 2]

ZHANG X D， ZHANG P， LIU H， et al. Fracture extended model under hydraulic fracturing engineering for high rank coal reservoirs［J］. Journal of China University of Mining & Technology，2013，42（4）：573-579.

[本文引用: 2]

[16]

于本福，闫相祯，杨秀娟，等.考虑储层孔隙介质分形特点的衰竭气藏储气库储层压力分布预测［J］.石油学报，2013，34（5）：1017-1022.

[本文引用: 1]

YU B F， YAN X Z， YANG X J， et al. Dynamic reservoir pressure prediction of depleted reservoir gas storage considering the fractal feature of porous medium［J］. Acta Petrolei Sinica，2013，34（5）：1017-1022.

[本文引用: 1]

[17]

徐刚，马瑞峰，牟全斌.煤层水力裂缝参数对煤层气井产气量的影响［J］.煤炭技术，2014，33（5）：243-246.

[本文引用: 1]

XU G， MA R F， MU Q B. Impact of hydraulic fracture parameters on production of coalbed methane wells［J］. Coal Te-chnology，2014，33（5）：243-246.

[本文引用: 1]

[18]

赵群，王红岩，李景明，等.快速排采对低渗透煤层气井产能伤害的机理研究［J］.山东科技大学学报：自然科学版，2008，27（3）：27-31.

[本文引用: 1]

ZHAO Q， WANG H Y， LI J M， et al. Study on mechanism of harm to CBM well capability in low permeability seam with quick drainage method［J］.Journal of Shandong University of Science and Technology：Natural Science，2008，27（3）：27-31.

[本文引用: 1]

... 煤层气产能预测是煤层气开采潜力评价的一项指标，对煤层气资源合理开发有着重要的指导意义^［1-2］.河南省作为产煤大省，煤层气资源极为丰富，全省埋深0~2 000 m的煤层气资源总储量超过1×10¹²m³，省内焦作矿区有近百年的煤炭开采历史，经多次矿井勘探与抽采技术评价，已经成为研究煤层气产能预测的理想场所^［3-5］.然而区内煤层存在典型的“三低一高”（低压、低渗、低饱和、高地质变动程度）地质特征，常规油气开采技术难以适用，因而在开发中需对储层进行压裂改造^［6-7］.迄今为止，国内外许多专家学者对煤层气井的产能预测进行了大量研究.岑学齐等^［8］在煤层气理想模型假设的基础上建立了计算产量所需各参数的方程，并结合产量计算方程和静态物质平衡方程推导出产能预测解析模型；吴静^［9］利用CBM-SIM煤层气数值模拟软件，深入分析了煤层厚度、渗透率、含气量、吸附性、储层压力、含气饱和度和临储比等煤储层因素对煤层气井产能的影响；王保辉等^［10］考虑煤岩面割理和端割理2个方向不同的渗流性质，建立了煤岩割理正交各向异性数学模型，并对鄂尔多斯盆地东部煤层单井产能进行了模拟计算；王琰琛等^［11］基于平行板理论和等值渗流阻力原理，建立了考虑吸附、解吸和扩散特征的煤层气藏连续等效介质模型，并计算分析了煤层气藏压裂直井的IPR曲线；PANTEHA等^［12］考虑储层几何形状、煤层气井底压力和流体速度等因素，提出了预测煤层气产能的方法；郭肖等^［13］基于煤岩双孔单渗模型、砂岩单孔单渗模型和煤岩与砂岩层间窜流模型，构建了煤层气与砂岩气合采的数值模型，并对影响合采产能和层间窜流强度的因素进行了敏感性分析. ...

... 煤体在成岩与改造过程中，在自重应力与构造应力的作用下会导致岩体内部形成大量的原生裂隙.由文献［14］可知储层原生裂隙的间距、宽度和密度对水力裂缝起裂与延伸有着重要影响，因此要想准确反映水力裂缝扩展延伸规律，必须考虑储层基于原生裂隙几何特征的起裂压力.由于原生裂隙强度问题已经不符合材料力学研究范围，而断裂力学的强度理论恰能够解决裂隙性煤岩体的破裂问题，此时含有原生裂隙几何特征参数的垂直井起裂压力模型可表示为： ...

... 水力裂缝在延伸过程中，筒侧壁破裂应力P_i折减为延伸应力P_ys，结合张小东等^［15］对煤层水力裂缝在延伸过程中应力状态以及其压降衰减规律的研究可知，距井壁x处的裂缝内净压力关于位置x变化的关系式可表示为： ...

... 由文献［15］可知，滤失到地层中的压裂液体积可表示为： ...

... 根据于本福等^［16］对储层压力分布的研究，储层压力动态变化的数学物理方程为： ...

... 在排采阶段，假设煤层气在压裂缝端部为径向流，在中部为单向流，则垂直井煤层气总产能计算公式可表示为^［17］： ...

... 由于研究区煤层倾角较小，因此可认为煤层初始储层压力在垂直井影响范围内是恒定的^［18］.边界压力可表示为： ...

〈

〉