一种基于BP神经网络的气井重复压裂井优选方法

霍雅迪; 江厚顺

doi:10.11764/j.issn.1672-1926.2020.01.004

天然气地球科学 >

2020 , Vol. 31 >Issue 4: 552 - 558

DOI: https://doi.org/10.11764/j.issn.1672-1926.2020.01.004

天然气开发

一种基于BP神经网络的气井重复压裂井优选方法

霍雅迪 ,
江厚顺

展开

长江大学石油工程学院，湖北武汉 430100

江厚顺（1969-），男，安徽怀宁人，教授，博士，主要从事油气田开发研究.E-mail：jhs_hust@sina.com.

霍雅迪（1995-），女，天津人，硕士研究生，主要从事油气田开发研究.E-mail: 469156935@qq.com.

收稿日期: 2019-11-06

修回日期: 2020-01-18

网络出版日期: 2020-04-26

收起

A preferred method for gas well re-fracturing well based on BP neural network

Ya-di HUO ,
Hou-shun JIANG

Expand

Yangtze University Petroleum Engineering，Wuhan 430100, China

Received date: 2019-11-06

Revised date: 2020-01-18

Online published: 2020-04-26

Fold

本文亮点

目前我国一些气田经过初次压裂后，增产效果不明显，或生产一段时间后，产量明显下降。为了提高气井的产量，可对气井进行重复压裂。进行重复压裂优选，可使气井得到较好的压裂效果。分析了影响气井重复压裂效果的因素，可分为地质因素和工程因素2部分。地质因素包括孔隙度、渗透率、表皮系数、产层厚度、含气饱和度、地层压力系数及剩余可采储量，工程因素包括前一次压裂是否成功、前一次压裂液用量、前一次压裂加砂量。基于BP神经网络理论，结合气井重复压裂效果影响因素分析，建立了重复压裂井优选模型。使用粒子群算法对其进行了优化，提高收敛速度的同时有效防止了局部最优解情况的发生，预测重复压裂井的日产气量，以此为依据优选重复压裂井。通过对C区重复压裂效果预测表明，基于BP神经网络优选重复压裂井可以提高选井的准确性。

本文引用格式

霍雅迪 , 江厚顺 . 一种基于BP神经网络的气井重复压裂井优选方法[J]. 天然气地球科学, 2020 , 31(4) : 552 -558 . DOI: 10.11764/j.issn.1672-1926.2020.01.004

Highlights

At present, after initial fracturing in some gas fields, the effect of increasing production is not obvious, or after a period of production, the output is significantly reduced. In order to increase the production of gas wells, the gas wells can be repeatedly fractured. It is preferred to carry out repeated fracturing to obtain a better fracturing effect of the gas well. The factors affecting the effect of repeated fracturing of gas wells are analyzed. The influencing factors are divided into two parts: geological factors and engineering factors. Geological factors include porosity, permeability, skin coefficient, production layer thickness, gas saturation, formation pressure coefficient, remaining recoverable reserves and engineering factors include the success of the previous fracturing, the amount of fracturing fluid used in the previous fracturing, and the amount of sand added during the previous fracturing. Based on BP neural network theory, combined with the analysis of influencing factors of gas well repeated fracturing effect, the optimal model of re-fracturing well was established. The particle swarm optimization algorithm was used to optimize it. While increasing the convergence rate, it effectively prevented the occurrence of local optimal solutions, and predicted the daily gas production rate of the repeated fracturing wells. Based on this, the repeated fracturing wells were optimized. By predicting the effect of repeated fracturing in Zone C, it is better to repeat the fracturing well based on BP neural network to improve the accuracy of well selection.

0 引言

由于对压裂地层情况认识不清晰或者受到压裂工艺和设备的限制，会产生一些压裂失效井。而之前产量得到短期提高的压裂见效井，随着开采的进行，初次压裂时产生的有效裂缝不断闭合或堵塞，再加上井底污染等原因，导致产量不断下降。根据气井的生产历史数据、气田动态监测结果，并结合气田开发现状分析造成生产下降的根本原因，再结合现场实际情况优选具有增产潜力^[1,2]的气井进行重复压裂^[3,4,5]是解决上述问题的最有效途径。重复压裂选井选层是高度非线性数学问题，马晓彬等^[6]结合了模糊数学和灰色关联方法对气井优选，杨小松等^[7]、闫文华等^[8]应用模糊数学方法结合层次分析法对气井进行了评判，李春月等^[9]结合了多元回归与模糊识别的方法对重复压裂井进行优选。以上论述的方法对重复压裂选井和气井选井分别有一定的指导意义，但忽略了气藏生产情况^[10]对重复压裂的影响，且选出的井局限性较强。本文以XX气田C区气藏为研究对象，通过对气井的重复压裂效果进行影响因素分析，结合BP神经网络法建立模型，根据C区气藏现场生产数据对该区的气井进行日产量预测，优选出适合进行重复压裂的气井，提高了重复压裂选井的效率和准确性，具有较好的指导意义。

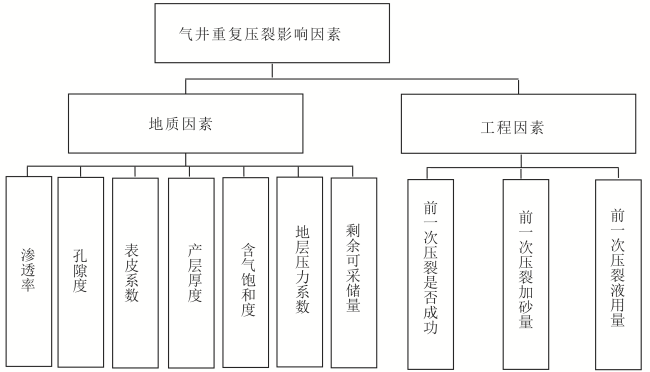
1 气井重复压裂效果影响因素分析

气井重复压裂的效果是多个特征参数共同作用的结果。确定压裂方案前，选取具有压裂价值的井层^[11,12,13]，影响着整个压裂作业的效果。对于井层的优选，主要根据已有的生产数据进行压裂分析^[14,15,16]。但由于原始数据单位不同或缺失，所以，本文对收集到的数据做预处理后进行了特征参数的影响分析，选取了孔隙度、渗透率、表皮系数、产层厚度、含气饱和度、地层压力系数、剩余可采储量、原油密度、原油黏度、地层温度等地质因素和前一次压裂是否成功、前一次压裂液用量、前一次压裂加砂量等工程因素作为分析气井重复压裂效果的因素，并利用熵值法确定了各因素的权重。

熵代表所有因素的混乱程度，熵值的大小与不确定性的大小呈正相关。通过熵的特点可以确定因素的重要程度。第一评估指标的熵值可以定义为：

H j = - ∑ i = 1 m f i j L n f i j L n m

（1）

f i j = b i j ∑ i = 1 m b i j

（2）

计算评价指标的熵值A：

A = a i j 1 × n

（3）

a j = 1 - H j n - ∑ j = 1 n H j, ∑ j = 1 n a j = 1

（4）

按照熵值排序最终确定了以下10个因素，为预测模型的建立奠定了基础。

计算出的权重如表1所示。确定的影响因素如图1所示。

表1 影响因素权重

Table 1 Impact factor weight

影响因素	权重
渗透率	0.12
孔隙度	0.06
表皮系数	0.18
产层厚度	0.06
地层压力系数	0.12
含气饱和度	0.06
剩余可采储量	0.25
前一次压裂是否成功	0.06
前一次压裂加砂量	0.045
前一次压裂液用量	0.045

显示原图|下载原图ZIP|生成PPT

图1 气井重复压裂影响因素

Fig.1 Factors influencing repeated fracturing of gas wells

2 选井选层模型的建立

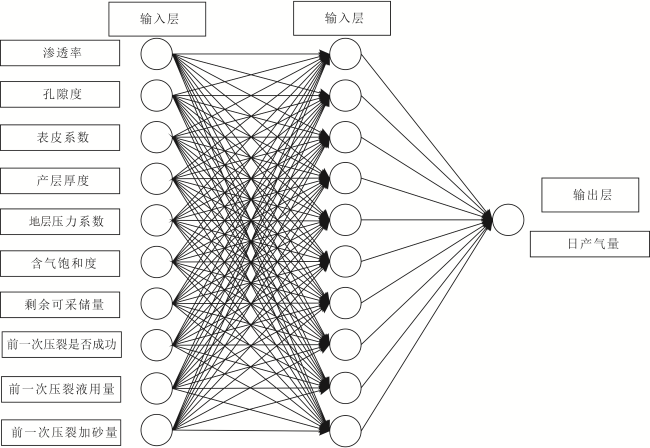
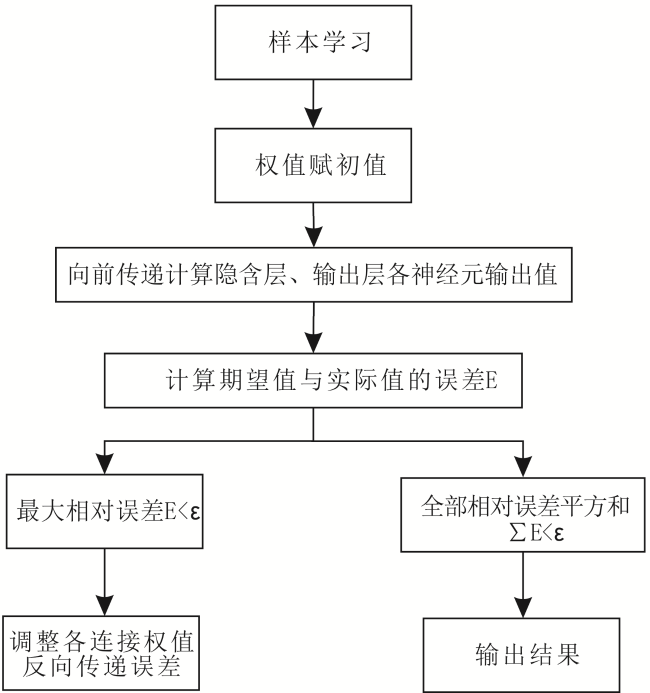
2.1　BP神经网络模型

选取输入层节点数为10，中间层节点数为16，输出层节点数为1。

BP神经网络法层次结构如图2。BP神经网络法优选井步骤如图3。

显示原图|下载原图ZIP|生成PPT

图2 BP神经网络法层次图

Fig.2 BP neural network method hierarchy

显示原图|下载原图ZIP|生成PPT

图3 BP神经网络法优选井步骤

Fig.3 BP neural network method preferred well step

（1）初始化BP神经网络，对神经网络的权值

{ω j i}

、

v k j

和阈值

θ j

、

r k

赋初值，通常把初值赋值较小，而且是随机产生。

（2）输入初次学习模式，即将现场压裂施工的气井的各特征参数以及压裂效果作为学习样本。

（3）将所赋的初值作为输入层的输出

I i

，用输入层到中间层的权值

{ω j i}

和阈值

θ j

，求出对中间层单元j的输入

U j

以及相应的输出

H j

。

U j = ∑ i ω j i I i + θ j

（5）

H j = f U j

（6）

f为Sigmoid函数：

f x = 1 + e - x - 1

（7）

（4）用中间层的输出

H j

，中间层到输出层的连接权值

v k j

以及输出层单元k的阈值

r k

，根据式(12)与式(13)求出对输出层单元k的输入

S k

以及相应的输出

O k

。

S k = ∑ j v k j H j + γ k

（8）

O k = f S k

（9）

（5）根据学习模式的信号

T k

和输出层的输出

O k

的差求出有关输出层单元的阈值以及连接到其上的权值的误差

δ k

。

δ k = O k - T k O k 1 - O k

（10）

（6）根据误差

δ k

，从中间层到输出层的权值

v k j

，以及中间层的输出

H j

，求出有关中间层单元j的偏置值以及连接到其上的权值的误差

σ j

。

σ j = ∑ k δ k v k j H j 1 - H j

（11）

（7）根据式(10)求出的

δ k

以及

H j

和常数

α

，对从中间层单元j到输出层单元k的权值

v k j

加以调整，根据

δ k

和常数

β

对输出层单元k的阈值

r k

加以调整。

v k j = v k j + α δ k H j

（12）

r k = r k + β δ k

（13）

（8）根据式(11)求得的误差

σ j

，输入单元i的输出

I i

以及常数

α

，对从输入单元i到中间单元j的连接权值

ω j i

加以调整。根据误差

σ j

和常数

β

对之间层单元j的阈值

θ j

加以调整。

ω j i = ω j i + α σ j I i

（14）

θ j = θ j + β σ j

（15）

循环上述过程，直至学习次数小于规定次数。为了确保BP神经网络优选井的准确性，需要设置合适的学习率，并且在样本学习时要保证足够的样本量，以此来建立更贴近油田实际的映射关系，从而合理的指导气井选井。

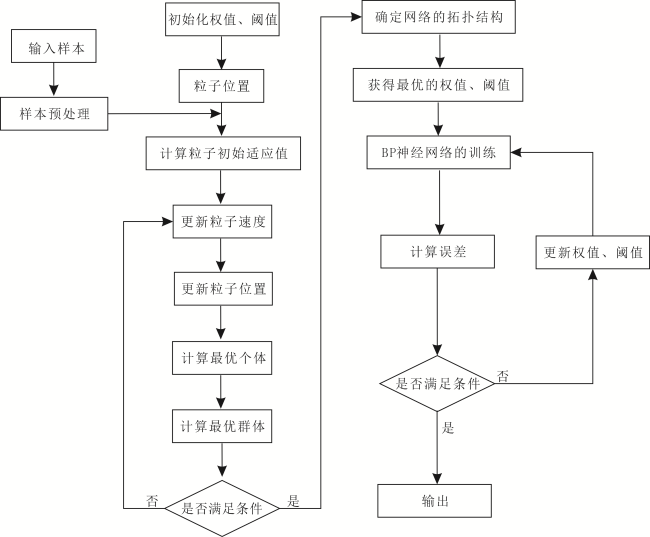
2.2　PSO-BP神经网络模型

可以利用粒子群算法来对BP神经网络的初始值进行优化，提高收敛速度的同时有效防止局部最优解情况。

PSO-BP 神经网络的运算过程如图4所示：

显示原图|下载原图ZIP|生成PPT

图4 PSO-BP神经网络法优选井步骤

Fig.4 PSO-BP neural network method to optimize well steps

速度、位置可采用式(16)和式(17)分别来进行更新。

V i d k + 1 = ω V i d k + c 1 r 1 P i d k - X i d k + c 2 r 2 P g d k - X g d k

（16）

X i d k + 1 = X i d k + V i d k + 1

（17）

式中：

ω

为惯性权重；k为迭代次数；

V i d

为运行速度；

c 1

、

c 2

为加速因子；

r 1

、

r 2

为两个随机函数，取值范围是

0,1

，粒子的位置和速度一般分别设定在

X m i n, X m a x

和

V m i n, V m a x

区间内。

运用PSO优化权值和阈值，进而确定出粒子的维数，如式(18)所示：

D = I × H + H × O + H + O

（18）

式中：

I

为输入层节点数；

H

为隐含层节点数；

O

为输出层节点数。

粒子个数为20，迭代次数为100，加速常数

c 1

c 2

=2,位置变化设置在

X m i n, X m a x

中，速度变化设置在

V m i n, V m a x

中。其中

X m i n

=-5，

X m a x

=5，

V m i n

=-1，

V m a x

=1。粒子维数D=193，惯性权值最大值

W m a x = 0.9

，惯性权值最小值

W m i n

=0.4。

3 实例计算

XX气田位于鄂尔多斯盆地，该气田累计探明储量为1.1×10⁸m³，其中C区为该气田的一个区块。C区块具有低渗[（0.18~1.95)×10^-3μm²]、低压(压力系数为0.86~0.91)、低丰度[(0.9~2.2)×10⁸m³/km²]的特点，孔隙度为5.1%~12.7%，C区基本上没有比较大的有效砂体，且非均质性强，部分井层砂体甚至没有有效厚度，部分井层砂体有效厚度在1.5~12.3 m之间。投产前套压为20~35 MPa，目前油压为1.5~8 MPa。由于储层的物性差，很多老井在生产一段时间后，产量下降明显，含水率猛增，原有裂缝形成水通道，有效砂体基本失效，所以需要进行重复压裂。重复压裂改造是改善C区储层渗流条件、提高储量动用程度的关键技术。

分别将选定的学习样本和检测样本导入，进行样本学习。学习样本如表2，检测样本如表3。由于样本学习检测需要大量数据，此处只截取部分数据。

表2 学习样本

Table 2 Learning samples

井号	渗透率/（10^-3µm²）	孔隙度/%	表皮因子	产层厚度/m	地层压力系数	含气饱和度/%	剩余可采储量/(10⁴m³）	前一次压裂是否成功	前一次压裂加砂量/t	前一次压裂液用量/m³	日产气量/（10⁴m³/d）
A1	0.36	7.81	1.5	9.4	0.85	50.8	1 926	1	29.6	218.6	0.78
A2	0.51	8.52	3.9	3.6	0.87	49.6	1 514	0	19.1	142.3	0.25
A3	0.38	6.58	3.1	8.2	0.84	64.1	2 102	1	40.1	248.2	0.91
A4	0.69	8.91	0.3	3.1	0.85	46.3	1 507	0	16.9	141.1	0.22
A5	0.52	8.51	2.3	8.6	0.87	62.6	1 635	1	22.6	168.6	0.85
A6	0.55	7.89	1.8	8.1	0.86	51.5	1 712	1	23.1	172.5	0.78
A7	0.49	8.32	3.6	2.9	0.85	48.2	1 593	0	19.8	146.4	0.17
A8	0.41	9.13	0.9	3.5	0.87	60.3	1 779	1	25.4	185.4	0.96
A9	0.28	6.7	2.7	4.8	0.86	56.8	1 987	1	27.3	196.6	0.99
A10	0.62	9.22	0.9	5.6	0.82	49.2	1 395	0	14.2	136.2	0.23
A11	0.59	8.84	0.6	3.9	0.84	47.9	1 429	0	17.5	158.3	0.31
A12	0.38	6.94	2.6	6.7	0.87	57.3	2 592	1	34.8	226.5	1.05
A13	0.54	9.12	0.5	3.2	0.82	46.5	1 457	0	20.3	152.9	0.23
A14	0.41	6.43	2.8	6.1	0.87	53.8	2 004	1	36.6	236.6	1.06
A15	0.29	7.15	2.5	7.3	0.87	59.3	1 896	1	32.8	212.2	0.98
A16	0.58	8.87	0.8	5.2	0.83	48.1	1 416	0	18.4	138.4	0.19
A17	0.34	6.72	3.3	8.4	0.86	56.2	1 938	1	40.2	269.4	1.18
A18	0.62	8.37	0.6	4.9	0.82	45.7	1 509	0	20.6	152.6	0.32
A19	0.45	6.88	1.9	6.5	0.86	58.5	1 793	1	33.7	208.9	0.98
A20	0.36	7.16	2.7	7.6	0.87	63.2	2 398	1	41.6	273.2	1.16

表3 检测样本

Table 3 Test samples

井号	渗透率/（10^-3µm²）	孔隙度/%	表皮因子	产层厚度/m	地层压力系数	含气饱和度/%	剩余可采储量/（10⁴m³）	前一次压裂是否成功	前一次压裂加砂量/t	前一次压裂液用量/m³	日产气量/(10⁴m³/d)
B1	0.39	8.26	2.5	4.5	0.87	53.3	1 778	1	21.9	144.2	0.76
B2	0.57	6.29	0.7	2.4	0.82	47.6	1 429	0	22.5	185.8	0.23
B3	0.43	9.82	2.4	5.6	0.86	65.2	2 354	1	38.2	243.6	1.12
B4	0.69	7.16	1.1	3.1	0.81	51.5	1 532	0	23.4	181.7	0.34
B5	0.62	6.78	0.1	2.8	0.83	44.7	1 569	0	18.2	143.8	0.39
B6	0.37	7.37	2.8	8.9	0.87	63.4	2 013	1	37.2	230.6	1.15
B7	0.45	8.58	3.2	3.5	0.86	52.9	2 516	1	19.5	146.5	0.78
B8	0.58	7.34	2.6	7.4	0.87	54.9	1 496	1	29.7	219.9	0.87

将8口候选井各特征参数导入，进行预测，BP神经网络计算结果如表4。

表4 BP神经网络计算结果

Table 4 BP neural network calculation results

井号	渗透率/(10^-3µm²）	孔隙度/%	表皮因子	产层厚度/m	地层压力系数	含气饱和度/%	剩余可采储量/(10⁴m³)	前一次压裂是否成功	前一次压裂加砂量/t	前一次压裂液用量/m³	预测日产气量/（10⁴m³/d）
C1	0.42	8.37	2.1	2.5	0.81	45.3	1 752	0	17.9	114.2	0.39
C2	0.51	6.12	0.7	2.3	0.82	57.1	1 829	0	22.5	185.7	0.56
C3	0.63	9.82	0.5	5.6	0.87	65.2	2 306	1	40.3	261.2	0.68
C4	0.74	11.16	1.1	3.1	0.81	55.3	1 637	0	45.4	251.7	0.51
C5	0.67	8.78	2.1	2.8	0.85	44.7	1 589	1	37.2	226.8	0.92
C6	0.37	6.37	2.8	8.9	0.81	63.4	2 213	1	39.3	240.2	0.35
C7	0.49	8.42	3.2	3.4	0.86	51.5	2 812	0	18.5	138.4	0.98
C8	0.38	7.56	1.8	10.1	0.84	52.9	1 993	0	28.7	212.3	0.75

根据预测日产气量的大小进行排序，日产气量越大，越适合压裂。可以得到候选井由优到劣的排序是C7、C5、C8、C3、C2、C4、C1、C6，优选出的井为C7、C5、C8。C7井目前累产气较少，剩余可采储量较丰富，可对C7井进行压裂设计，并进行重复压裂改造。再结合对C7井上一次压裂失败的原因分析，发现C7井前一次压裂规模较小，裂缝闭合快，没有有效地沟通气层，因此可对C7井重新设计并施工。同时对C5井、C8井进行重新设计并施工。

重新设计C7井压裂加砂量为115.4 m³，压裂液用量为1 058.6 m³。经过压裂措施后，压裂初期日产气大约为1.12×10⁴m³/d，近期油套压分别为1.28 MPa、3.15 MPa，随后日产气量稳定在0.88×10⁴m³/d，增产0.63×10⁴m³/d，预测误差率为11.8%。C5井日产稳定在0.76×10⁴m³/d，误差率为21.1%，误差较大，可能是由于该井累产气达到3 086.55×10⁴m³，目前该井已经采出的产气量较丰富，导致误差偏大，可考虑对C5井周围邻井进行重复压裂改造。C8井日产稳定在0.68×10⁴m³/d，误差率为8.7%。C7井、C5井、C8井重复压裂取得了成功。

4 结论

（1）分析了影响气井重复压裂效果的因素，充分考虑了前一次压裂的效果，利用熵值法确定了各因素的权重，基于BP神经网络算法建立了相关计算模型。

（2）利用粒子群算法对BP神经网络模型的初始值进行优化。编制相应的计算软件，对C区部分井进行预测，根据日产气量大小进行排序，优选出适合重复压裂的井分别为C7井、C5井、C8井。

（3）现场对优选出的井进行重复压裂，得到C7井、C5井、C8井平均日产气量分别为0.88×10⁴m³/d、0.76×10⁴m³/d、0.68×10⁴m³/d。实际产气量与预测结果基本一致，表明基于BP神经网络优选气井重复压裂井能提高选井的准确性。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

1	胡永全,林辉,赵金洲,等.重复压裂技术研究[J].天然气工业,2004，(3):72-75，147. HU Y Q, LIN H, WANG S Z, et al. Study on repetitive fracturing technology[J]. Natural Gas Industry,2004，(3):72-75，147.

2	赵金洲,尹庆,李勇明,等.重复压裂气井热—固耦合应力场拟三维模型[J].天然气地球科学,2015,26(11):2131-2136. Zhao J Z, Yin Q, Li Y M, et al. A pseudo-three-dimensional model for thermoelastic stress oiled around a re-fractured gas well [J].Natural Gas Geoscience,2015 26(11):2131-2136.

3	邵先杰,董新秀,汤达祯,等.韩城矿区煤层气中低产井治理技术与方法[J].天然气地球科学,2014,25(3):435-443. Shao X J, Dong X X, Tang D Z, et al. Control technology and method for low and medium production wells in coalbed methane in Hancheng mining area [J].Natural Gas Geoscience,2014,25(3):435-443.

4	MAUNISH S, SUBHASH S, ANIRBID S. A comprehensive overview on recent developments in refracturing technique for shale gas reservoirs[J]. Journal of Natural Gas Science and Engineering,2017,46：350-364.

5	YANCHAO L, YUNBIN H, JIANFENG X, et al. Optimal selection and effect evaluation of re-fracturing intervals in shale gas horizontal wells[J]. Natural Gas Industry B,2018，38（7）：59-64.

马晓彬,周文,钱春华.模糊数学和灰色关联相结合的水力压裂选井选层评判方法研究[J].物探化探计算技术,2013,35(3):369-372, 252.

X B

， ZHOU

， QIAN

C H

，et al. Study on judgment method of hydraulic fracturing and well selection by combining fuzzy mathematics and grey relation[J]. Computing Techniques for Geophysical and Geochemical Exploration,2013,35(3):369-372, 252.

7	杨小松,孙良田,孙雷,等.模糊数学在气井压裂酸化选井选层因素分析中的应用[J].钻采工艺,2005, 28(4)：39-43，16-17. YANG X S, SUN L T, LIU Y B, et al. Application of fuzzy mathematics for factors analysis of wells and layers choice in fracturing and acidizing gas wells[J]. Drilling & Production Technology,2005,28(4):39-43，16-17.

8	闫文华,魏勋,潘洪灏,等.应用模糊综合评判方法优选水力压裂井[J].数学的实践与认识,2011,41(19):69-74. YAN W H, WEI X, PAN H H, et al. Optimizing hydraulic fracturing wells with the method of fuzzy comprehensive evaluation[J].Mathematics in Practice and Theory,2011,41(19):69-74.

9	李春月,张士诚,马新仿.多元回归与模糊识别相结合优选重复压裂井[J].内蒙古石油化工,2009,35(3):132-133. LI C Y, ZHANG S C, MA X F. Repetitive fracturing wells by combining multiple regression with fuzzy recognition[J].Inner Mongolia Petrochemical Industry,2009,35(3):132-133.

10	SOPHIE S Y, MUKUL M S. A new method to calculate slurry distribution among multiple fractures during fracturing and refracturing[J]. Journal of Petroleum Science and Engineering,2018,170：304-314.

11	龚杨,张秦汶,王楠.模糊识别方法在压裂选井选层中的应用[J].重庆科技学院学报：自然科学版,2013,15(6):59-61，74. GONG Y, ZHANG Q W, WANG N. Application of well selection for fracturing by fuzzy recognition method[J].Journal of Chongqing University of Science and Technology：Social Sciences Edition,2013,15(6):59-61，74.

12	姜梅枝.低渗透重复压裂井选层研究[J].油气井测试,2012,21(2):37-40，43，76-77. JIANG M Z. Research on layer selection in low permeability and re-fracturing well[J]. Well Testing,2012,21(2):37-40，43，76-77.

13	位云生,胡永全,赵金洲,等.人工神经网络方法在水力压裂选井评层中的应用[J].断块油气田,2005，12(4):42-44，91-92. WEI Y S, HU Y Q, ZHAO J Z, et al. Application of artificial nerve network method to evaluating & choosing target layer well in hydraulic fracturing treatment[J]. Fault-Block Oil and Gas Field, 2005，12(4):42-44，91-92.

14	张洲,鲜保安,连小华,等.低渗煤储层背景下高渗带主控地质因素及模式[J].天然气地球科学,2018,29(11):1656-1663. ZHANG Z, XIAN B A, LIAN X H, et al. Main geological factors and models of high permeability zone under the background of low permeability coal reservoir [J].Natural Gas Geoscience,2018,29(11):1656-1663.

15	杨晓盈,李永臣,朱文涛,等.贵州煤层气高产主控因素及甜点区综合评价模型[J].天然气地球科学,2018,29(11):1664-1671，1678. YANG X Y, LI Y C, ZHU W T, et al. Main control factors of guizhou coalbed methane high yield and comprehensive evaluation model for dessert areas[J].Natural Gas Geoscience,2018,29(11):1664-1671, 1678.

16	吕志凯,贾爱林,唐海发,等.大型致密砂岩气藏水平井产能评价与新认识[J].天然气地球科学,2018,29(6):873-879. LÜ Z K, JIA A L, TANG H F, et al. Productivity evaluation and new understanding of horizontal wells in large tight sandstone gas reservoirs[J]. Natural Gas Geoscience, 2018,29(6):873-879.

Options

文章导航

模态框（Modal）标题

本文亮点

本文引用格式

Highlights

0 引言

1 气井重复压裂效果影响因素分析

表1 影响因素权重

图1 气井重复压裂影响因素

2 选井选层模型的建立

2.1 BP神经网络模型

图2 BP神经网络法层次图

图3 BP神经网络法优选井步骤

2.2 PSO-BP神经网络模型

图4 PSO-BP神经网络法优选井步骤

3 实例计算

表2 学习样本

表3 检测样本

表4 BP神经网络计算结果

4 结论

参考文献

2.1　BP神经网络模型

2.2　PSO-BP神经网络模型