天然气地球科学 >

2020 , Vol. 31 >Issue 3: 340 - 347

DOI: https://doi.org/10.11764/j.issn.1672-1926.2019.12.008

天然气开发

多孔介质速度场和流量场分布

  • 戚涛 , 1 ,
  • 胡勇 2 ,
  • 李骞 , 1 ,
  • 彭先 1 ,
  • 赵潇雨 3 ,
  • 荆晨 4
展开
  • 1. 中国石油西南油气田公司勘探开发研究院，四川 成都 610041
  • 2. 中国石油西南油气田公司，四川 成都 610051
  • 3. 中国石油西南油气田公司工程技术研究院，四川 成都 610051
  • 4. 中国石油西南油气田公司页岩气研究院，四川 成都 610051
李骞（1984-），男，四川成都人，高级工程师，博士，主要从事复杂气藏开发机理、开发动态预测、数值模拟等研究.E-mail：.

戚涛（1988-）,男，四川南充人，工程师，博士，主要从事油气藏渗流理论和数值模拟研究.E-mail：.

收稿日期: 2019-09-05

  修回日期: 2019-12-14

  网络出版日期: 2020-03-26

收起

Velocity and flow field in porous media

  • Tao QI , 1 ,
  • Yong HU 2 ,
  • Qian LI , 1 ,
  • Xian PENG 1 ,
  • Xiao-yu ZHAO 3 ,
  • Chen JING 4
Expand
  • 1. Research Institute of Exploration and Development, PetroChina Southwest Oil & Gasfield Company, Chengdu 610041, China
  • 2. PetroChina Southwest Oil & Gasfield Company, Chengdu 610051, China
  • 3. Research Institute of Engineering Technology, PetroChina Southwest Oil & Gasfield Company, Chengdu 610051, China
  • 4. Research Institute of Shale Gas, PetroChina Southwest Oil & Gasfield Company, Chengdu 610051, China

Received date: 2019-09-05

  Revised date: 2019-12-14

  Online published: 2020-03-26

Supported by

The China National Science and Technology Major Project During the 13th Five-year Plan Period(2016ZX05052-002)

The Major Science and Technology Projects of CNPC(2016E-0605)

Fold

本文亮点

流体在多孔介质中的宏观特性由介质本身的孔隙结构直接决定，速度场和流量场作为连接微观和宏观的桥梁显得尤为重要，但相关的研究相对较少。基于孔隙网络模型中的流动模拟，采用欧拉描述方法，系统统计了多孔介质中速度和流量的分布，分析了速度和流量的概率密度函数随孔隙结构的变化关系。研究表明：①随多孔介质无序性的增加，速度的分布范围急剧增加，流量的分布范围变化不大；②速度的概率密度函数随无序因子的减小依次表现为：高斯分布、指数分布、指数截断的幂律分布及幂律分布，流量的概率密度函数主要受孔隙非均质性的影响，表现为高斯分布和指数截断的幂律分布；③归一化流体速度的平均值受变异系数和配位数共同影响，且与配位数成乘幂关系，归一化流体流量的平均值不随配位数的变化而变化，但其随变异系数的增加而降低。

本文引用格式

戚涛 , 胡勇 , 李骞 , 彭先 , 赵潇雨 , 荆晨 . 多孔介质速度场和流量场分布[J]. 天然气地球科学, 2020 , 31(3) : 340 -347 . DOI: 10.11764/j.issn.1672-1926.2019.12.008

Highlights

The macroscopic properties characterizing fluid transport in porous media are directly determined by the pore structure of the media itself. Velocity field and flow field, connecting microscopic and macroscopic theories, are particularly important, but few studies have been carried out. Based on the simulation of single-phase flow in pore network model, this paper systematically calculated the distribution of Eulerian velocity and flow in porous media, and analyzed the relationship between pore structure and the probability density function of velocity and flow. And the following research results were obtained. Firstly, with the increase of the disorder of porous media, the distribution range of velocity increases sharply, while that of flow rate does not change much. Secondly, as the disorder factor decreases, the probability density function of velocity satisfies the following distributions in turn: Gauss distribution, exponential distribution, power law with exponential cut-off distribution and power law distribution. The probability density function of the flow is mainly affected by the heterogeneity of porous media, which basically obeys Gauss distribution and power law with exponential cut-off distribution. Thirdly, the average value of the normalized fluid velocity(v*) is affected by both the coefficient of variation and the coordination number, and the relationship between v* and the coordination number obeys power law. The average value of normalized fluid flow(q*) does not change with coordination number, but decreases with the increase of the coefficient of variation.

0 引言

在医学、水文地质、石油工程及化学工程等不同领域，黏性流体或溶质在多孔介质中的输运是相当复杂的，这种复杂性源于多孔介质孔隙结构的随机性和不同流体颗粒间的相互作用[1,2,3]。表征流体流动和颗粒输运的宏观特性（如渗透率、地层因素、电阻率指数）直接取决于多孔介质几何结构的相关参数（如孔隙连通性、孔隙半径变异系数及迂曲度等），但两者间的关系是不具有普遍性的[4,5]。
不可压缩流体在特定多孔介质中的流动属性包括速度场和流量场，两者是连接多孔介质的孔隙结构与传输属性、流体流动的微观与宏观理论的纽带。速度场控制着流体突破时间，流量场决定着流体流动和颗粒输运的主要通道，两者转换的关键在于孔隙半径分布。速度场和流量场均可以通过实验[6,7,8,9,10,11]和数值仿真[12,13,14,15,16]方法进行研究，但学者为了分析其与多孔介质孔隙结构间的关系，提出了概率密度函数分析方法，并得到了速度分布的唯象模型：拉伸指数分布[17]和幂指数分布[18]，但都没有基于统计物理理论。因此，本文基于多孔介质网络模型的流动模拟，采用欧拉描述方法，深度剖析了不同多孔介质无序性下速度场和流量场的变化规律。

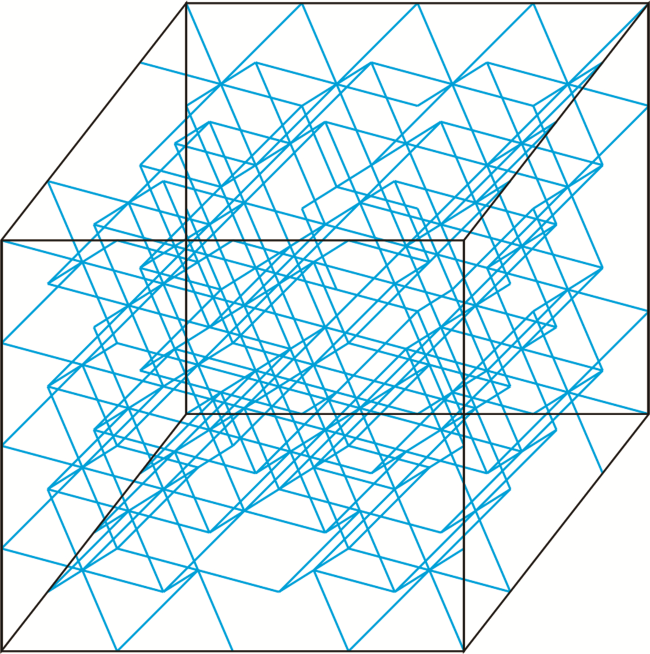
1 孔隙介质网络模型的建立

孔隙介质常用几何结构特征参数和拓扑结构特征参数联合表征，其中几何结构特征参数主要包括孔隙平均半径（或水力半径）、孔隙半径变异系数、孔隙长度、形状因子等；拓扑结构参数主要指配位数等。孔隙和喉道是根据某一界限划分的，两者都是流体流动的载体，其本质没有区别，区分孔隙和喉道对研究流体的传输属性并没有实质影响。因此，引入部分特征参数，参照多孔介质网络模型的构建方法[19,20]，建立了模型大小为25×25×25的体中心网格（BCC）的三维随机网络模型，该模型为“管束模型”，孔隙截面形状为圆形（图1)孔隙半径服从均匀对数分布（图2），可根据式（1）和式（2）联合求解确定孔隙半径分布的最大值r max和最小值r min；在均匀对数分布下的水力半径R与平均孔隙半径 r满足式（3）。孔隙长度l为水力半径的7.5倍。体中心网络模型的最大配位数为8，其余特定配位数可通过断开管束的方式获得，为防止传导率系数矩阵变为奇异矩阵，断开管束的半径设置为一个相当小的数值（如10-10 m），而连通管束服从均匀对数分布。
C V = r m a x + r m i n L n r m a x / r m i n 2 r m a x - r m i n - 1
R = r m a x + r m i n 2
r = R 1 + C V 2
式中：CV为孔隙半径变异系数，无因次；r max为孔隙半径最大值，m；r min为孔隙半径最小值，m；R为水力半径，m； r为平均孔隙半径，m。
图1 大小为5×5×5的体中心网络模型示意

Fig.1 BCC model with size of 5×5×5

图2 水力半径为40 μm时不同变异系数下孔隙半径分布

Fig.2 The radius distribution under different CV with R=40 μm

2 流体的流动模拟

与两相流动和颗粒输运相比，单相流体的流动更为简单，其宏观流动属性与多孔介质微观孔隙结构的关联性更为直接。一般情况下，单相流体在圆管的流动满足Hagen-Poiseuille方程，即管束流量为：
q = 10 9 × π r 4 8 l Δ p μ
式中：q为管束流量，m3/s；r为管束半径，m；l为管束长度，m； Δ p为管束两端的压差，MPa；μ为流体黏度，mPa·s。
根据质量和能量守恒定律，流体在节点均遵循Kirchoff定律，即：
∑ k = 1 z i q = 0
式中： zi为与节点i相连的总管束数。
根据式（4）和式（5）可以列出一系列线性方程组，写成矩阵形式如式（6）。在给定模型两端压力的情况下，利用共轭梯度法求解模型的压力场分布。
A P = 0
式中： A为传导率系数矩阵； P为模型各个节点压力组成的向量。
根据网络模型压力场分布和管束的传导率公式，运用式（4）即可求得所有管束的流量，再利用式（7）计算得到模型流速场分布。
v = q π r 2

3 模拟结果

以枫丹白露砂岩孔隙结构为参考，在保证水力半径（R=40 μm）、孔隙长度（l=300 μm）、宏观平均流体速度（U=10-4 m/s）不变的情况下，改变变异系数（CV=0.05，0.55和1.05）和配位数（z=2.8，3.2，4.0，4.8，6.4和8.0）以模拟不同多孔介质中的流体流动，模拟渗透率均大于100×10-3 µm。孔隙半径变异系数CV和配位数z均是多孔介质无序性的表征参数，变异系数越大，则孔隙半径差异越大，大孔隙和小孔隙越多，但对于孔隙介质，大孔隙不会成片发育，流体渗流过程仍受小孔隙主导，导致渗流能力偏低；配位数越小，则孔隙连通率越低，流体流动的通道越少，从而降低渗透性。因此，引入多孔介质无序因子F dis（ F d i s = z / C V），F dis越小，多孔介质无序性越强。
拉格朗日法和欧拉法常用于描述流体运动和颗粒输运，两者的区别在于拉格朗日法侧重于“质点”，而欧拉法侧重于“场”，因此，采用欧拉法描述多孔介质中所有孔隙的属性参数更为合适。同时，为描述、量化及对比不同多孔介质的传输属性参数，以完全均质且完全连通的BCC网络模型的参数为标准，将孔隙结构参数与传输属性参数进行归一化处理，即： r * = r i / R， v * = v i / 3 U， q * = q i / q 0， 其中 q 0 = 3 π R 2 U。

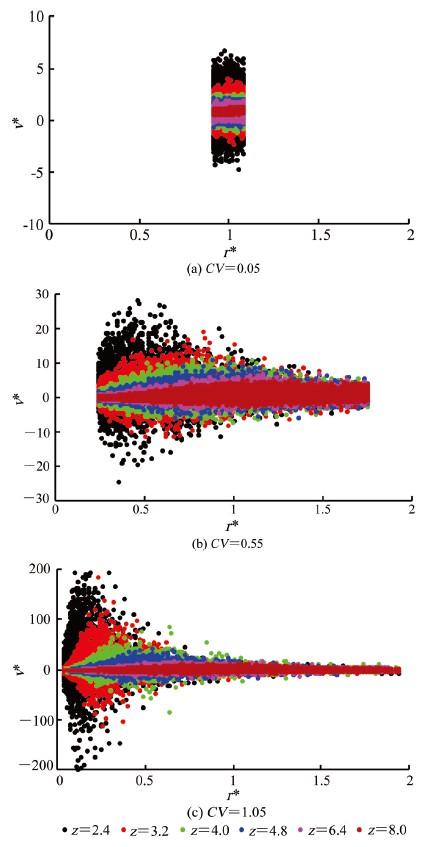
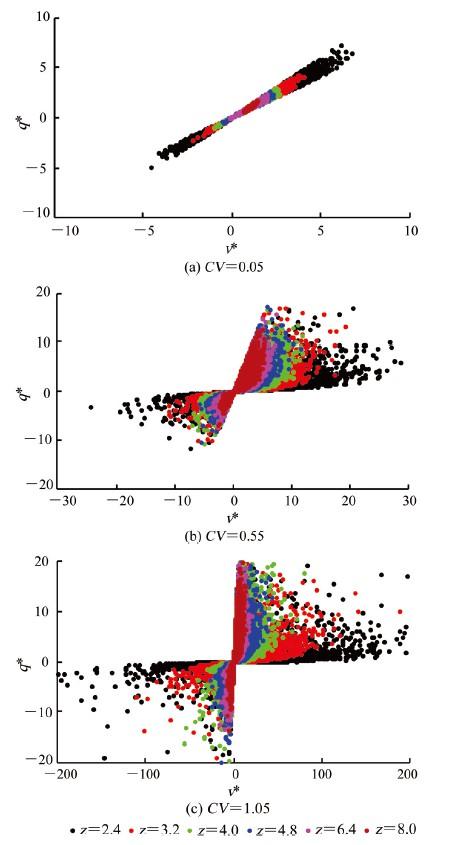
3.1　多孔介质速度场

图1为归一化孔隙流体速度v *与归一化孔隙半径r *的关系图版，v *为负值代表该孔隙中的流体发生反向流动（与整体流动方向相反）。总体上看，随着变异系数的增加，孔隙流体速度的非均质性增强，大孔隙流体速度变化较小，而小孔隙流体速度波动范围急剧增加，这主要因为孔隙半径服从对数均匀分布，小孔隙占比较高，导致小孔隙出现大流速的概率增加。
对于均质网络（CV=0.05），v *与r *呈条带型分布；当网络模型完全连通（z=8）时，孔隙流体速度均为正值，即流体只沿着主要压力梯度方向流动，不会发生反向流动，且v *基本围绕1上下波动，振幅较小；随着配位数的降低，v *的变化范围增大，孔隙流体速度出现负值，流体在局部发生反向流动，形成涡旋[图3(a)]。随着变异系数的增加，条带型分布转变为无规律的分布形态[图3(b)，图3(c)]；同时，连通性越差，v *的波动范围越大，小孔隙出现大流速的概率越大，且v *与r *近似表现为长尾分布形态。
图3 不同F dis下的v *与r *关系

Fig.2 The relationship between v *and r * under different F dis

流体速度为负值或正值的概率分布形态类似，因此仅以正值的流体速度为主研究v *的概率分布形态（图4）。v *分布范围较广，介于10-5~103之间；随着多孔介质无序性的增强，小v *占比增加，孔隙流体速度差异增大，v *最小值变化不大，仍在10-5数量级，v *最大值增加近2个数量级。v *概率分布受变异系数和配位数共同影响，其随无序因子F dis减小大致经历4个阶段：高斯分布、指数分布、指数截断的幂律分布及幂律分布[21]，拟合结果见表1。
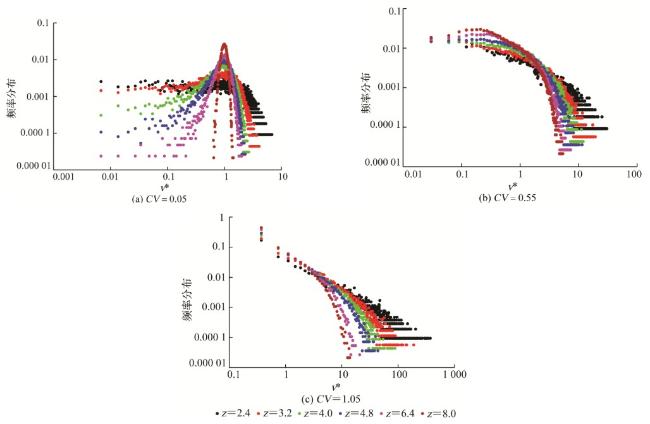
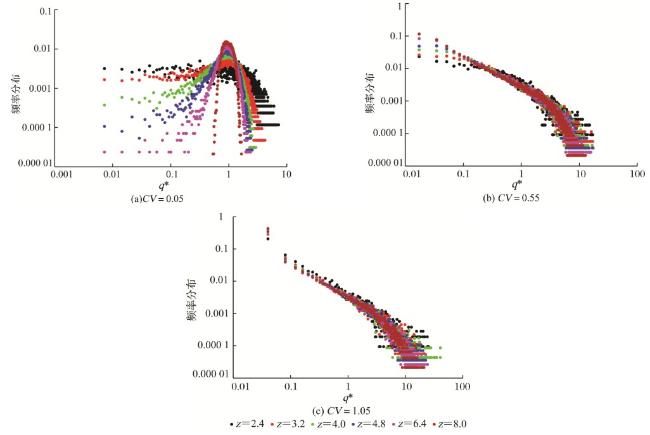
图4 不同F dis下的v *概率分布

Fig.4 The probability distribution of v * under different F dis

表1 v *概率分布函数拟合参数

Table 1 Fitting parametersof probability distribution function of v *

CV z F dis

拟合

函数类型

函数

表达式

A

a 1,a 2,a 3,a 4

B

b 1,b 2,b 3,b 4

C

c 1, c 3

D

d 1
0.05 8 160 高斯分布 y = a 1 + b 1 e - x - c 1 2 2 d 1 2 -0.000 078 4 0.026 04 0.995 52 0.105 04
0.05 6.4 128 0.000 137 5 0.012 54 0.999 41 0.208 11
0.05 4.8 96 0.000 147 6 0.008 78 1.002 14 0.293 43
0.05 4 80 0.000 092 9 0.006 54 1.006 99 0.396 85
0.05 3.2 64 0.000 043 3 0.003 89 1.022 11 0.668 77
0.05 2.4 48 指数分布 y = a 2 e b 2 x 0.002 57 -0.409 99 — —
0.55 8 14.55 0.030 89 -1.106 71 — —
0.55 6.4 11.64 0.024 98 -0.923 85 — —
0.55 4.8 8.72 0.018 65 -0.740 07 — —
0.55 4 7.27 指数截断的幂律分布 y = a 3 e b 3 x x c 3 0.014 65 -0.612 32 -0.029 09 —
0.55 3.2 5.82 0.009 62 -0.406 97 -0.157 08 —
0.55 2.4 4.36 0.006 38 -0.256 04 -0.318 91 —
1.05 8 7.61 0.098 49 -0.359 83 -0.799 22 —
1.05 6.4 6.09 0.081 53 -0.201 02 -0.978 95 —
1.05 4.8 4.57 0.071 46 -0.082 54 -1.108 40 —
1.05 4 3.80 0.069 14 -0.073 14 -1.078 36 —
1.05 3.2 3.04 0.051 62 -0.063 26 -0.810 05 —
1.05 2.4 2.28 幂律分布 y = a 4 x b 4 0.036 57 -0.994 33 — —

注： a 1，a 2，a 3，a 4，b 1，b 2，b 3，b 4，c 1，c 3，d 1均为拟合系数；余同

由表1可知，当F dis>60时，v *概率分布服从高斯分布；当8<F dis<60时，v *概率分布服从指数分布；当3<F dis<8时，v *概率分布服从指数截断的幂律分布；当F dis<3时，v *概率分布服从幂律分布。观察b 3和c 3可以发现，随着F dis的减小，b 3逐渐接近0，而c 3逐渐远离0，展示了v *概率分布由指数分布向幂律分布的过渡。
根据统计的孔隙流体速度，计算了归一化流体速度的平均值<v *>（图5）。对于均质介质（CV=0.05），<v *>约等于1，且不随配位数的变化而变化。对于连通性较好的网络，<v *>随变异系数的增加而减小；对于连通性较差的网络，<v *>随变异系数的增加而增加，且<v *>基本满足乘幂规律； v * ∝ z - z c - b v，b v随着变异系数的增加而增加。
图5 归一化流体速度的平均值<v *>

Fig.5 The average value of normalized fluid velocity<v *>

3.2　多孔介质流量场

图4为归一化流体流量q *和归一化流体速度v *的关系图版，与v *一样，q *为负值表示流体发生反向流动产生的流量。总体上看，q *变化范围远小于v *变化范围，因此由公式q *=πr*2 v *可以发现大孔隙常为小流速，而大流速常出现在小孔隙中；正向流动的流体流量最大值大于反向流动的流体流量最大值，从侧面体现了流体的主要流动方向。
有序网络（CV=0.05，z=8）中的流体均发生正向流动，流体流量均为正值；稍微增加网络的无序性就会出现反向流动，继而产生反向流量[图6(a)]。当CV ≥0.55时，正向流动的q *与v *分布形态与反向流动的q *与v *分布形态基本类似，且关于点（0，0）成对称分布[图6(b), 图6(c)]。当变异系数相同时，配位数越低，发生反向流动的孔隙占比越大，产生的反向流量占比越大，在一定程度上阻止了流体的正向流动，进而降低了模型的渗透率。
图6 不同F dis下的q *与v *关系图版

Fig.6 The relationship between q *and v * under different F dis

随着变异系数的增加，归一化流体流量q *概率分布越趋近于一致，小数值q *（q *<0.1）占比大幅增加，大数值q *（q *>1）占比逐渐减小（图7）。大流量孔隙对多孔介质中的流体流动起主导作用，而小流量孔隙的影响微乎其微，大数值q *平均值的增大及占比的减小越发突显了大流量孔隙的重要地位。若多个大流量孔隙相连通，贯穿整个多孔介质，将形成一条或多条流体流动的优势通道。
图7 不同F dis下的q *概率分布

Fig.7 The probability distribution of q * under different F dis

当CV=0.05时，q *概率分布与v *的分布类似，表现为高斯分布向指数截断的幂律分布过渡；当CV≥0.55时，小数值q *概率分布在一定程度上受到配位数影响，但大数值q *概率分布几乎没有变化，表现出了一致性。结合q *概率分布的形态，以高斯分布和指数截断的幂律分布对q *概率分布进行拟合，拟合结果如表2。
表2 q *概率分布函数拟合参数

Table 2 Fitting parametersof probability distribution function of q *

CV z F dis

拟合

函数类型

函数

表达式

A

a 1,a 3

B

b 1,b 3

C

c 1,c 3

D

d 1
0.05 8 160 高斯分布 y = a 1 + b 1 e - x - c 1 2 2 d 1 2 -0.001 05 0.015 84 0.982 29 0.213 35
0.05 6.4 128 0.000 102 3 0.010 98 0.973 58 0.253 37
0.05 4.8 96 0.000 145 6 0.008 49 0.974 16 0.321 78
0.05 4 80 0.000 152 5 0.006 69 0.978 92 0.407 66
0.05 3.2 64 0.000 081 6 0.004 41 0.996 01 0.672 11
0.05 2.4 48 指数截断的幂律分布 y = a 3 e b 3 x x c 3 0.006 04 -0.784 40 -0.398 86 —
0.55 8 14.55 0.002 69 -0.103 72 -0.960 91 —
0.55 6.4 11.64 0.002 92 -0.134 28 -0.915 36 —
0.55 4.8 8.73 0.003 41 -0.211 55 -0.848 22 —
0.55 4 7.27 0.004 28 -0.349 79 -0.716 06 —
0.55 3.2 5.82 0.005 85 -0.574 17 -0.517 17 —
0.55 2.4 4.36 0.008 00 -0.760 78 -0.237 33 —
1.05 8 7.62 0.003 67 -0.145 82 -0.923 54 —
1.05 6.4 6.09 0.003 65 -0.140 49 -0.926 81 —
1.05 4.8 4.57 0.003 73 -0.137 93 -0.947 17 —
1.05 4 3.81 0.003 39 -0.102 91 -1.028 72 —
1.05 3.2 3.05 0.003 48 -0.081 51 -1.049 74 —
1.05 2.4 2.28 0.004 22 -0.119 34 -1.071 45 —
指数截断的幂律分布融合了指数分布和幂律分布，其拟合效果将优于指数分布和幂律分布。由表2可以发现：CV=0.55对应的b 3整体小于CV=1.05对应的b 3，即CV=1.05对应的b 3更接近于0，说明随着变异系数的增加，q *概率分布服从指数分布类型的减弱；同时CV=0.55对应的c 3整体大于CV=1.05对应的c 3，说明随着变异系数的增加，q *概率分布服从幂律分布类型的增强。总体而言，随着变异系数的增加，q *概率分布更偏重于幂律分布。
与<v *>不同，归一化流体流量的平均值<q *>不随配位数的变化而变化，但其随变异系数的增加而降低（图8）。达西公式揭示了多孔介质的渗透率与横截面的流体流量成正比，即k *∝N<q *>，其中k *为归一化渗透率，N为横截面上的平均有效孔隙个数。因此，当孔隙连通性一定时，增加孔隙半径变异系数将降低<q *>，进而降低模型的渗透率；类似地，当变异系数一定时，降低孔隙连通性，横截面上的有效孔隙数N将减少，最终导致模型渗透率的降低。换言之，增加多孔介质的无序性将降低渗透率。
图8 归一化流体流量的平均值<q *>

Fig.8 The average value of normalized fluid flow <q *>

4 结论

利用网络模型模拟多孔介质中的流体流动，采用欧拉描述方法，结合统计学理论，探索分析了速度场和流量场分布与多孔介质无序性的关系，主要得到以下结论：
--引用第三方内容--

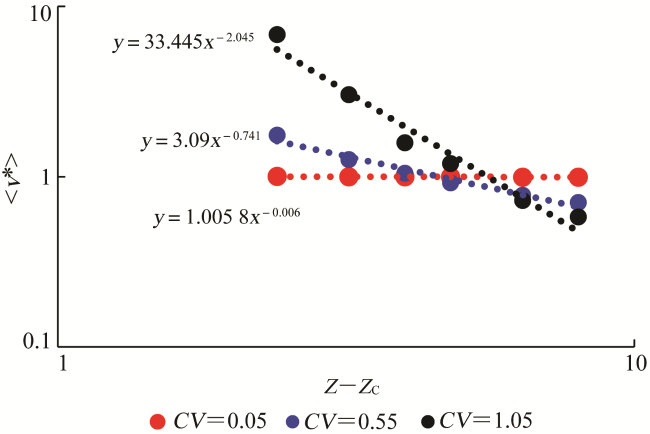
（1）速度场受孔隙非均质性和孔隙连通性共同影响，其概率密度函数随无－序因子的降低逐渐表现为：高斯分布、指数分布、指数截断的幂律分布及幂律分布；归一化流体速度的平均值与配位数满足乘幂规律： v * ∝ z - z c - b v，b v随着变异系数的增加而增加。

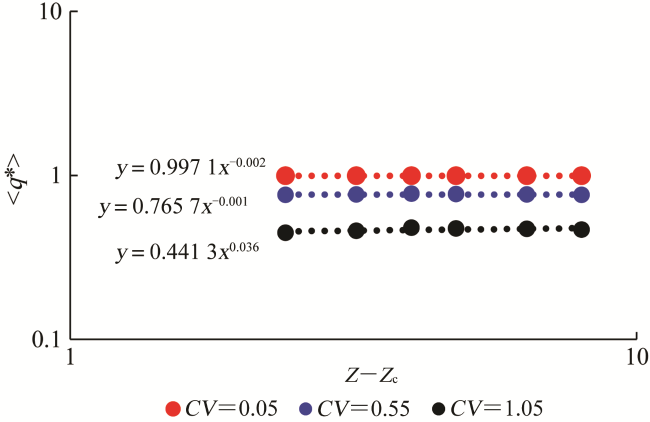
（2）流量场受孔隙非均质性的影响较大，受孔隙连通性的影响较小，其概率密度函数主要表现为高斯分布和指数截断的幂律分布；归一化流体流量的平均值随变异系数的增加而降低，但不随配位数的变化而变化。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
1
PENTA R, AMBROSI D. The role of microvascular tortuosity in tumor transport phenomena and future perspective for drug delivery[J]. PAMM, 2015, 15(1): 101-102.

2
BOISSON A, DE ANNA P, BOUR O, et al. Reaction chain modeling of denitrification reactions during a push-pull test[J]. Journal of Contaminant Hydrology, 2013, 148: 1-11.

3
ORR F M, TABER J J. Use of carbon dioxide in enhanced oil recovery[J]. Science, 1984, 224(4649): 563-569.

4
DARDIS O, MCCLOSKEY J. Permeability porosity relationships from numerical simulations of fluid flow[J]. Geophysical Research Letters, 1998, 25(9): 1471-1474.

5
CHEN C, PACKMAN A I, Gaillard J F. Pore‐scale analysis of permeability reduction resulting from colloid deposition[J]. Geophysical Research Letters, 2008, 35(7)：L07404.

6
HOLZNER M, MORALES V L, WILLMANN M, et al. Intermittent Lagrangian velocities and accelerations in three-dimensional porous medium flow[J]. Physical Review E, 2015, 92(1): 013015.

7
CASSIDY R, MCCLOSKEY J, MORROW P. Fluid velocity fields in 2D heterogeneous porous media: Empirical measurement and validation of numerical prediction[J]. Geological Society, 2005, 249(1): 115-130.

8
MORAD M R, KHALILI A. Transition layer thickness in a fluid-porous medium of multi-sized spherical beads[J]. Experiments in Fluids, 2009, 46(2): 323-330.

9
MANSFIELD P, ISSA B. Fluid transport in porous rocks. I. EPI studies and a stochastic model of flow[J]. Journal of Magnetic Resonance： Series A, 1996, 122(2): 137-148.

10
KUTSOVSKY Y E, SCRIVEN L E, Davis H T,et al. NMR imaging of velocity profiles and velocity distributions in bead packs[J]. Physics of Fluids, 1996, 8(4): 863-871.

11
WU A, CHAO L, YIN S,et al. Pore structure and liquid flow velocity distribution in water-saturated porous media probed by MRI[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(5): 1403-1409.

12
ANDRADE J J S, COSTA U M S, Almeida M P, et al. Inertial effects on fluid flow through disordered porous media[J]. Physical Review Letters, 1999, 82(26): 5249.

13
LEBON L, OGER L, LEBLOND J,et al. Pulsed gradient NMR measurements and numerical simulation of flow velocity distribution in sphere packings[J]. Physics of Fluids, 1996, 8(2): 293-301.

14
DE ANNA P, QUAIFE B, BIROS G,et al. Prediction of the low-velocity distribution from the pore structure in simple porous media[J]. Physical Review Fluids,2017,2(12): 124103.

15
LEBON L, OGER L, LEBLOND J,et al. Pulsed gradient NMR measurements and numerical simulation of flow velocity distribution in sphere packings[J]. Physics of Fluids, 1996, 8(2): 293-301.

16
ZAMI-PIERRE F, DE LOUBENS R, QUINTARD M, et al. Transition in the flow of power-law fluids through isotropic porous media[J].Physical Review Letters,2016,117(7): 074502.

17
SIENA M, RIVA M, HYMAN J D, et al. Relationship between pore size and velocity probability distributions in stochastically generated porous media[J]. Physical Review E, 2014, 89(1): 013018.

18
MATYKA M, GOŁEMBIEWSKI J, KOZA Z. Power-exponential velocity distributions in disordered porous media[J]. Physical Review E, 2016, 93(1): 013110.

19
BERNABé Y, LI M, MAINEULT A. Permeability and pore connectivity: A new model based on network simulations[J]. Journal of Geophysical Research Atmospheres, 2010, 115(B10):172-186.

20
BERNABé Y, WANG Y, QI T, et al. Passive advection-dispersion in networks of pipes: Effect of connectivity and relationship to permeability[J]. Journal of Geophysical Research Solid Earth, 2016, 121(2):713-728.

21
ZHOU T, WANG B H, Jin Y D, et al. Modelling collaboration networks based on nonlinear preferential attachment[J]. International Journal of Modern Physics C,2007,18(2):297-314.

Options
文章导航

/

〈 〉

陇ICP备2021001824号-7　 甘公网安备 62010202000678号
版权所有 © 《天然气地球科学》编辑部
地址：甘肃省兰州市天水中路8号　
邮编：730000　
电话：(0931)8277790　
E-mail：geogas@lzb.ac.cn
总访问量 　 今日访问 　 在线人数
技术支持：北京玛格泰克科技发展有限公司