目前,针对裂缝参数与复杂性的判断方法主要分为3类:第一类是主压裂过程中水力裂缝空间几何形态实时评价技术;第二类是利用返排、试气数据或后期产量数据来推算裂缝参数;第三类是在压裂井附近重新钻井,通过取心来观察裂缝。其中,针对主压裂过程中水力裂缝空间几何形态实时评价技术,主要有微地震监测法、广域电磁法以及钻井取心观察。但是这些技术都存在明显的缺陷。首先,微地震事件只能粗略提供岩石剪切失效的地点,不能有效地探测拉伸失效,而后者是裂缝扩展的主要方式
[1,2]。这些微地震信号处理的不确定往往导致检测到的裂缝尺寸远远大于实际裂缝的尺寸。目前一种常用的处理方式是将微地震事件处理成热点图,微地震事件越密集说明存在裂缝的可能性越大,从而用来估计地层改造体积。但是这种方式目前还是不能有效地区分和估算天然裂缝和水力裂缝的面积。广域电磁法与微地震监测法类似,主要用来评估地层改造体积。同时,广域电磁法与微地震监测法由于观察范围有限并且设备费用高昂,致使此类技术在油田现场的推广应用受到了限制。利用返排、试气数据或后期产量数据来推算裂缝参数的技术,可以推算裂缝几何尺寸,但是需要测取一定时间的数据。对于优化压裂施工参数而言,不具有实时性。在压裂井附近钻井取心是一种直接观测水力裂缝和天然裂缝的技术,可以观察裂缝分布和支撑剂分布
[3],但是这种方法代价昂贵且耗时费力,除非在部分实验区块,否则不具有现场可行性。尽管压降分析是所有压裂施工中最常用的检测手段,但目前还没有针对复杂裂缝的压降分析模型及方法。



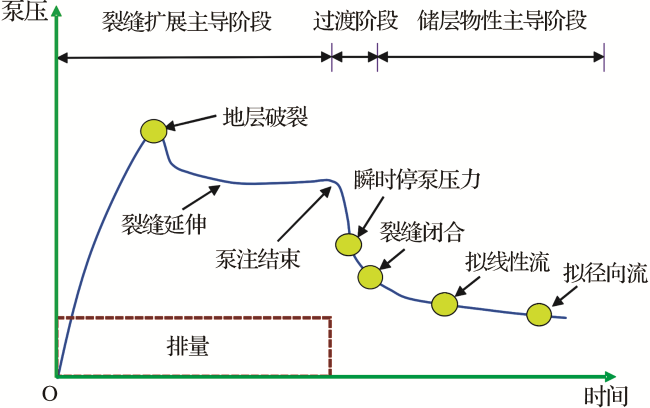
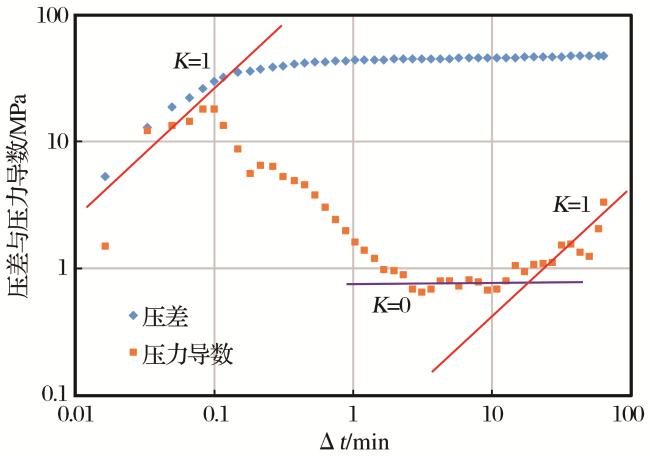
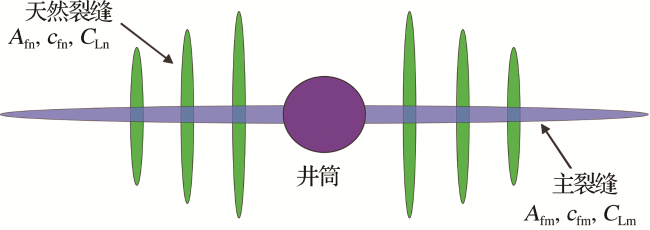
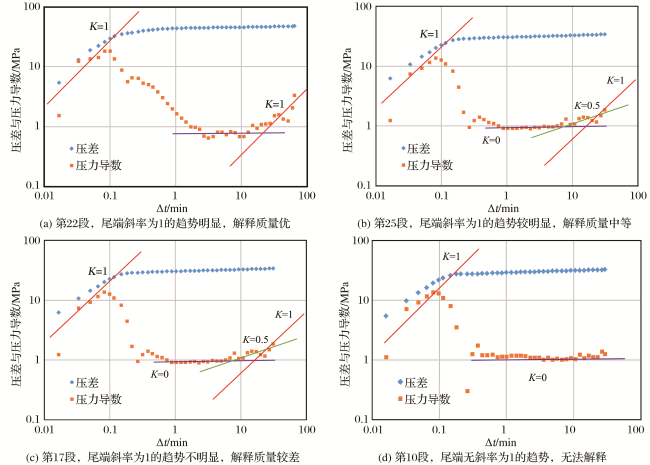
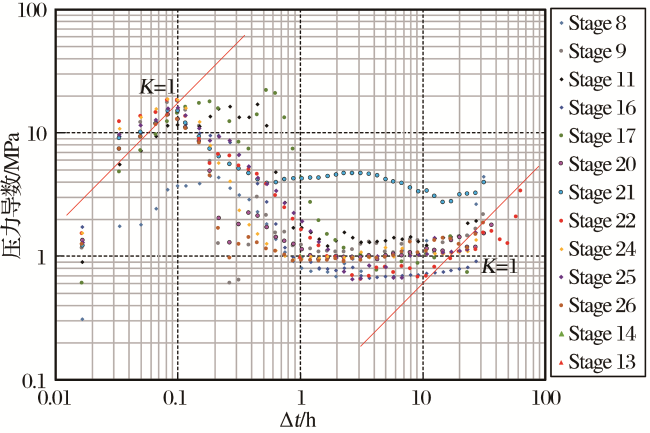
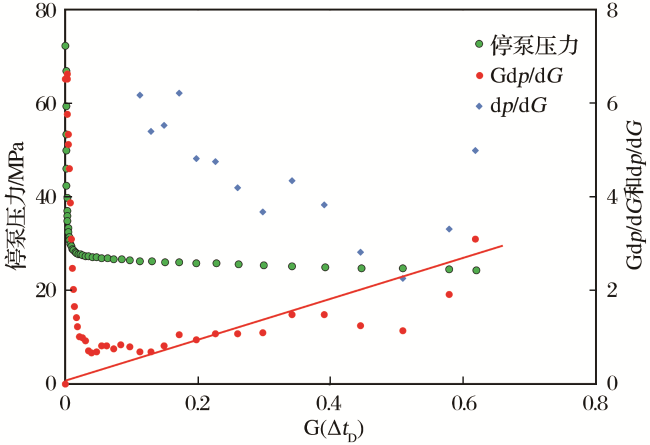
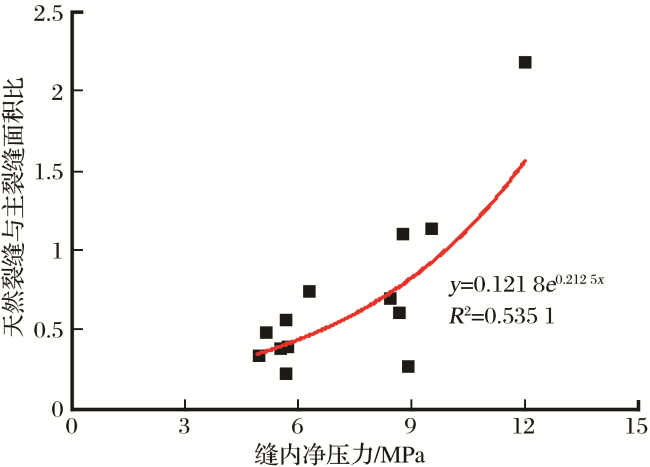
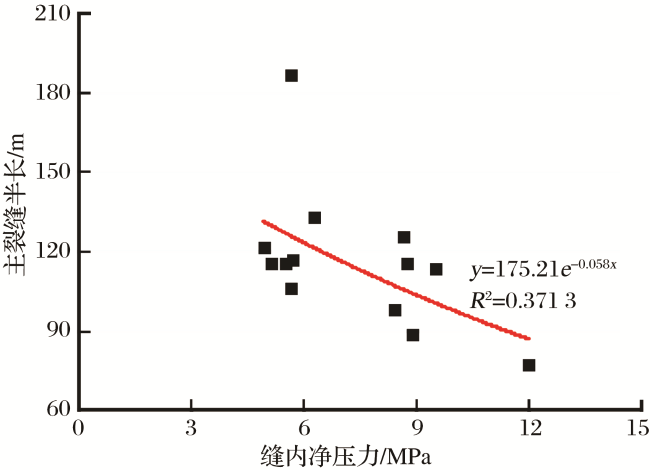
 甘公网安备 62010202000678号
甘公网安备 62010202000678号