0 引言
1 模型建立
1.1 温度正演预测模型
1.2 温度数据反演解释模型
1.2.1 误差函数
1.2.2 反演模型
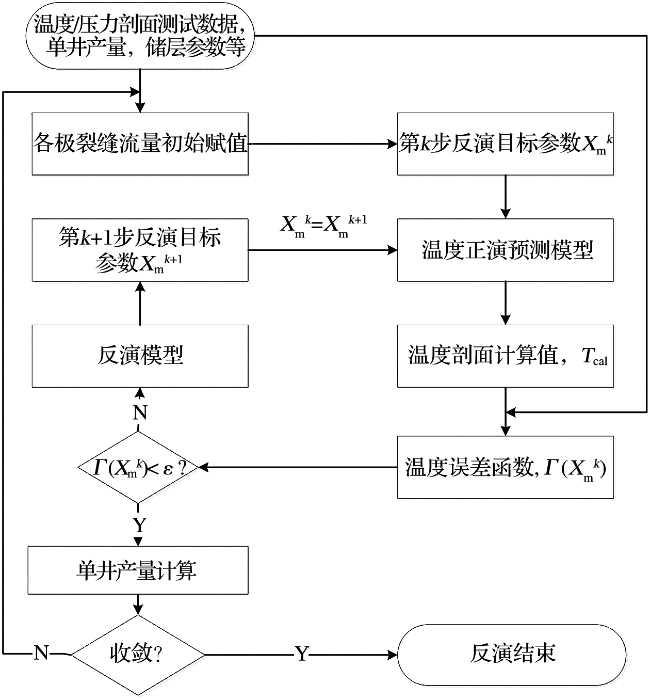
1.3 反演流程
2 实例应用
表1 模拟实例井基本参数Table 1 Basic parameters of the examples |
| 储层参数 | 气体物性参数(地面) | ||
|---|---|---|---|
| 储层长度/m | 1 000 | 气体密度/(kg/m3) | 0.9 |
| 储层宽度/m | 500 | 气体黏度/cP | 0.025 |
| 储层厚度/m | 20 | 体积系数/(m3/m3) | 0.004 |
| 储层顶深/m | 2 500 | 气体热容/[J/(kg·K)] | 2 550 |
| 孔隙度/% | 8 | 气体热导率/[J/(m·s·K)] | 0.000 26 |
| 水平渗透率/(×10-3μm2) | 0.1 | 热膨胀系数/(10-4/ K) | 10 |
| 垂向渗透率/(×10-3μm2) | 0.01 | 压缩系数/MPa-1 | 0.026 |
| 地面温度/K | 293 | ||
| 地温梯度/(K/m) | 0.02 | ||
| 储层温度/K | 343 | ||
| 地层压力/MPa | 30 | ||
| 井筒参数 | 储层岩石热学参数 | ||
| 水平段长度/m | 650 | 岩石密度/(kg/m3) | 2 380 |
| 井筒直径/m | 0.22 | 岩石热容/[J/(kg·K)] | 845 |
| 套管外径/m | 0.14 | 总导热系数/[J/(m·s·K)] | 3.46 |
| 套管内径/m | 0.12 | ||
| 井壁粗糙度/m | 0.001 5 | ||
| 套管导热系数/ [J/(m·s·K)] | 12 | ||
| 水泥环导热系数/ [J/(m·s·K)] | 6.9 | ||
表2 水平井井各级裂缝参数Table 2 Fracture parameters of the fractured horizontal well |
| 裂缝参数 | 裂缝1 | 裂缝2 | 裂缝3 | 裂缝4 | 裂缝5 | 裂缝6 |
|---|---|---|---|---|---|---|
| 裂缝半长/m | 180 | 120 | 200 | 100 | 150 | 200 |
| 裂缝宽度/m | 0.005 | 0.004 | 0.004 | 0.005 | 0.006 | 0.004 |
| 裂缝高度/m | 20 | 20 | 20 | 20 | 20 | 20 |
| 裂缝导流能力/(×10-3 μm2·cm) | 15 | 12 | 15 | 18 | 20 | 15 |
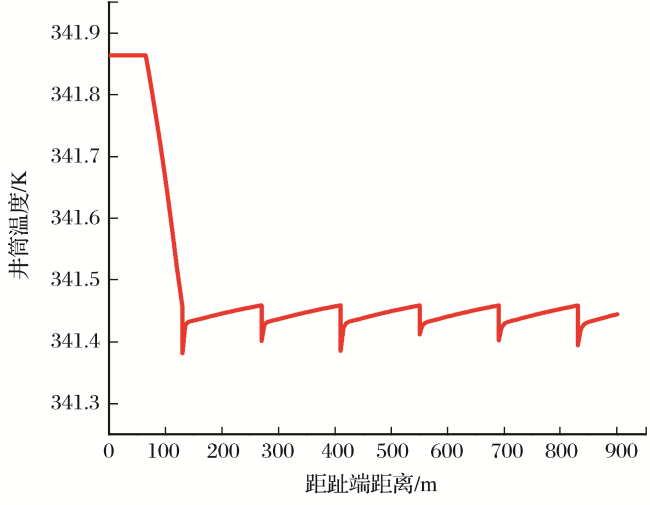
2.1 压裂水平井温度剖面特征
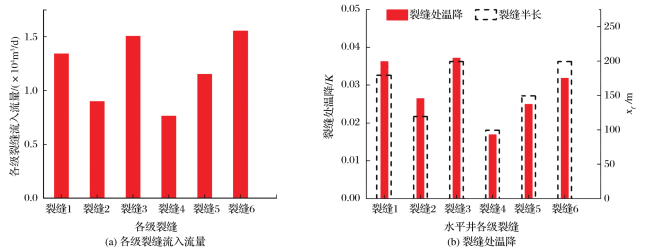
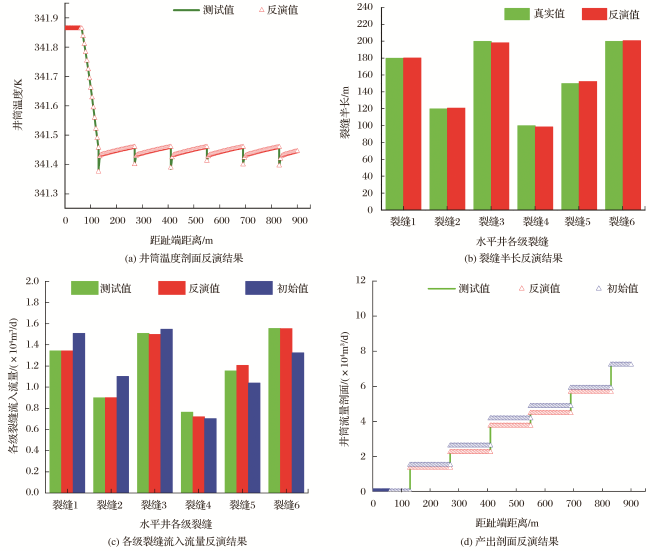
2.2 基于温度测试数据反演解释产出剖面
表3 模拟实例井产出剖面反演解释结果Table 3 Inversion results of the production profiles of the example well |
| 裂缝1 | 裂缝2 | 裂缝3 | 裂缝4 | 裂缝5 | 裂缝6 | |
|---|---|---|---|---|---|---|
| 测试温度/K | 341.381 3 | 341.401 4 | 341.385 3 | 341.412 0 | 341.402 3 | 341.394 2 |
| △T/K | 0.036 2 | 0.026 5 | 0.037 2 | 0.016 9 | 0.025 0 | 0.031 8 |
| 反演温度/K | 341.375 4 | 341.400 4 | 341.389 3 | 341.412 0 | 341.399 3 | 341.395 9 |
| 裂缝半长真实值/m | 180 | 120 | 200 | 100 | 150 | 200 |
| 裂缝半长反演值/m | 180.357 4 | 120.975 6 | 198.462 9 | 98.589 3 | 152.528 6 | 200.891 5 |
| 裂缝流入量测试值/(×104 m3/d) | 1.343 3 | 0.900 3 | 1.508 5 | 0.764 4 | 1.154 8 | 1.555 9 |
| 裂缝流入量反演值/(×104 m3/d) | 1.343 5 | 0.901 8 | 1.499 5 | 0.720 9 | 1.206 3 | 1.555 1 |
| 裂缝流入量初始值/(×104 m3/d) | 1.509 2 | 1.101 5 | 1.548 4 | 0.703 4 | 1.039 5 | 1.325 2 |



 甘公网安备 62010202000678号
甘公网安备 62010202000678号