基于多因素的煤储层气水两相非稳态流入动态评价方法及应用

doi:10.11764/j.issn.1672-1926.2023.03.016

基于多因素的煤储层气水两相非稳态流入动态评价方法及应用

张鹏^,¹, 王相春¹, 封从军², 郑力会¹, 张妍³, 孙萌思⁴

1.中国石油大学（北京），北京 102249

2.西北大学，陕西西安 710069

3.滨州学院，山东滨州 256600

4.延安大学，陕西延安 716000

Evaluation method and application of gas-water two-phase unsteady inflow performance of coal reservoir based on multiple factors

ZHANG Peng^,¹, WANG Xiangchun¹, FENG Congjun², ZHENG Lihui¹, ZHANG Yan³, SUN Mengsi⁴

1.China University of Petroleum （Beijing），Beijing 102249，China

2.Northwest University，Xi’an 710069，China

3.Binzhou University，Binzhou 256600，China

4.Yan’an University，Yan’an 716000，China

收稿日期: 2022-08-01 修回日期: 2023-03-27 网络出版日期: 2023-06-20

基金资助:

国家科技重大专项“多气合采钻完井技术和储层保护”. 2016ZX05066002-001

Received: 2022-08-01 Revised: 2023-03-27 Online: 2023-06-20

作者简介 About authors

张鹏（1980-），男，陕西渭南人，在读博士，工程师，主要从事煤层气开发研究.E-mail：apengysw@foxmail.com. , E-mail：apengysw@foxmail.com

摘要

煤层气开发中，流入动态是制定合理排采制度的重要依据，能够最大化延长稳产时间，提高最终产量。针对目前无井底压力与多因素的显式方程来评价非稳态流入动态的问题，采用理论推导和多因素拟合方法，建立了井底压力与时间、应力敏感系数、表皮系数、总产量、启动压力梯度的显式计算模型，同时结合生产数据对模型进行验证，并对井底压力的影响因素进行分析。结果表明，从初始生产阶段到压力稳定阶段，所建模型的准确率可达82.3%~94.76%，可有效评价多种因素对产量和井底压力的影响程度，为优化排采制度提供了技术支持。

关键词： 煤层气 ; 气水两相流 ; 非稳态 ; 多因素 ; 流入动态

Abstract

In the development of coalbed methane （CBM）， the inflow performance is an important basis for formulating a reasonable production system， which can maximize the stable production time and improve the final production. Aiming at the problem that there is no explicit equation of bottom hole pressure and multiple factors to evaluate the unsteady inflow performance， an explicit calculation model of bottom hole pressure and time， stress sensitivity coefficient， skin coefficient， total production， and start-up pressure gradient is established by using theoretical derivation and multiple factor fitting methods. The model is verified with production data， and the factors affecting the bottom hole pressure are analyzed. The results show that the accuracy of the model can reach 82.3%-94.76% from the initial production stage to the stable pressure stage， which can effectively evaluate the influence of various factors on production and bottom hole pressure， and provide technical support for optimizing the drainage system.

Keywords： CBM ; Gas-water two-phase flow ; Unsteady state ; Multiple factors ; Inflow performance

PDF (1410KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张鹏, 王相春, 封从军, 郑力会, 张妍, 孙萌思. 基于多因素的煤储层气水两相非稳态流入动态评价方法及应用. 天然气地球科学[J], 2023, 34(9): 1641-1651 doi:10.11764/j.issn.1672-1926.2023.03.016

ZHANG Peng, WANG Xiangchun, FENG Congjun, ZHENG Lihui, ZHANG Yan, SUN Mengsi. Evaluation method and application of gas-water two-phase unsteady inflow performance of coal reservoir based on multiple factors. Natural Gas Geoscience[J], 2023, 34(9): 1641-1651 doi:10.11764/j.issn.1672-1926.2023.03.016

0 引言

煤层气排采过程中，储层压力在时间和空间上都会发生动态变化，具体反映在井底压力（BHP）和产量的变化关系上，称为流入动态。流入动态研究对于制定合理的排采制度至关重要，其能够使供液与排液达到最优匹配，延长稳产时间，提高最终产能。

CLARKSON^［1］通过压力瞬变分析模型计算排采过程中平均储层压力，建立了饱和煤层气藏储层压降变化模型。SEIDLE^［2］介绍了平均储层压力动态变化数学模型和储层压降模拟方法。但平均储层压力仅反映某一阶段的整体压力大小，无法反映压力在空间上的分布情况^［3］。刘新福等^［4］以稳态渗流为前提，分别按照达西渗流和非达西渗流公式，结合表皮效应研究了煤层中水的产能与压差关系，以确定煤层气井合理的工作方式。杨红斌等^［5］在平面径向达西渗流基础上，考虑了启动压力和应力敏感因素对井底流压的影响。赵金等^［6］考虑表皮影响，根据达西定律描述了非稳态渗流下的压力分布。赵俊龙等^［7］考虑了煤储层开发过程中孔隙度和渗透率的动态变化，在平面径向非稳态达西渗流模型的基础上，研究了孔渗条件对压降传播的影响。张永平等^［8］基于达西渗流公式建立了外边界无限大、内边界分别为定产和定压条件下的井底流压动态预测模型。薛军等^［9］考虑了滑脱效应、启动压力梯度、应力敏感性、高速非达西流动及水锁损害等5个因素的稳态产能方程。朱维耀等^［10］考虑气水启动压力梯度和连续源，采用有限差分法求解方程得到两相产能变化规律。张先敏等^［11］考虑了启动压力梯度、表皮系数的煤层气非线性流动，得到了无因次井底压力与无因次时间的双对数关系图。

由此可见，目前的研究要么是基于稳态流动的多因素影响研究，无法将时间因素很好地结合起来，要么是将多个影响因素与非稳态流动进行了结合，但都是以拟压力函数与时间、各影响因素的关系为特征，无法直接给出实际压力的计算模型，不能直观表达压力与各因素的关系，难以制定直接、有效的生产策略；而对于以真实压力为基础的其他相关研究，如计算渗透率动态变化，则难以有效进行。

本文采用理论推导和多因素拟合方法，考虑表皮系数等多个因素，经过拟压力变换、无因次化、Laplace变换求解、Stehfest反演、拟合，得到无因次拟压力与无因次时间、表皮系数和启动压力梯度之间的关系式。分别以无因次拟压力、无因次时间为因变量，逐级分解、推导、二次拟合，最终得到井底压力与时间、应力敏感系数、表皮系数、总产量、气水启动压力梯度的显式关系式，揭示井底压力的变化规律，并评价各因素的影响程度。

1 气水两相非稳态渗流模型

首先通过基本假设构建物理模型，再根据连续性方程、流动方程，结合定解条件得到控制方程，最后通过无量纲化、Laplace变换求解。

1.1　基本假设

气水两相渗流物理模型主要考虑甲烷和水在裂隙中的渗流以及甲烷在孔隙中的运移，基质解吸扩散气体进入裂隙作为质量源考虑。做如下假设：①井型为直井，储层水平、等厚，且平面均质，流体在煤层中均匀分布；②储层上下边界封闭，外边界无限大；③忽略重力、毛管压力影响；④气体和水在裂隙中为非达西渗流，考虑启动压力梯度，孔隙中只有单相甲烷气体扩散，煤层气从基质扩散到割理、裂缝服从Fick第一定律；⑤地层压力变化会引发应力敏感，且井壁周围存在储层伤害；⑥煤层有效厚度不随气水产出发生变化，排采期间煤层微可压缩且保持恒温；⑦煤层中含水饱和度与含气饱和度之和为1，气体为真实气体，且忽略溶解气。

1.2　控制方程建立

1.2.1　气水渗流连续性方程

在文献［12］的连续性方程基础上，结合煤层气生产过程中不断解吸产生新气源的特点，增加了质量源项，见式（1）：

\begin{array}{l} - \frac{\partial (φ S_{g} ρ_{g})}{\partial t} + \frac{1}{r} \frac{\partial (r ρ_{g} v_{g})}{\partial r} + q_{m} = 0 \\ - \frac{\partial (φ S_{w} ρ_{w})}{\partial t} + \frac{1}{r} \frac{\partial (r ρ_{w} v_{w})}{\partial r} = 0 \end{array}

（1）

式中：φ为裂隙孔隙度，%；ρ_g为气体密度，g/cm³；S_g、S_w分别为裂隙中含气、含水饱和度，%；ρ_w为水的密度，g/cm³；v_g、v_w分别为裂隙中气体和水的径向渗流速度，m/s；r为径向距离，m；q_m为基质块单位时间内向裂隙系统的扩散流量，g/（cm³·s）；t为生产时间，s。

1.2.2　气水径向渗流速度方程

采用文献［13］的公式计算气水径向渗流速度，见式（2）：

\begin{array}{l} v_{g} = \frac{K K_{r g}}{μ_{g}} (\frac{\partial P}{\partial r} - G_{g}) \\ v_{w} = \frac{K K_{r w}}{μ_{w}} (\frac{\partial P}{\partial r} - G_{w}) \end{array}

（2）

式中：K为裂隙绝对渗透率，10^-3μm²；K_rg、K_rw分别为气、水的相对渗透率，无量纲；G_g、G_w分别为裂隙中气、水的拟启动压力梯度，MPa/m；μ_g、μ_w分别为气和水的黏度，mPa·s；P为裂隙中流体压力，MPa，是气和水的表观压力。

由式（1）和式（2）得到气相和水相的渗流控制方程：

\frac{\partial (φ S_{g} ρ_{g})}{\partial t} - \frac{1}{r} \frac{\partial}{\partial r} [r ρ_{g} \frac{K K_{r g}}{μ_{g}} (\frac{\partial P}{\partial r} - G_{g})] - q_{m} = 0

（3）

\frac{\partial (φ S_{w} ρ_{w})}{\partial t} - \frac{1}{r} \frac{\partial}{\partial r} [r ρ_{w} \frac{K K_{r w}}{μ_{w}} (\frac{\partial P}{\partial r} - G_{w})] = 0

（4）

式（3）与式（4）相加得：

\frac{1}{r} \frac{\partial}{\partial r} [r K (\frac{ρ_{g} K_{r g}}{μ_{g}} + \frac{ρ_{w} K_{r w}}{μ_{w}}) \frac{\partial P}{\partial r} - r K (\frac{ρ_{g} K_{r g}}{μ_{g}} G_{g} + \frac{ρ_{w} K_{r w}}{μ_{w}} G_{w})] = \frac{\partial}{\partial t} (φ S_{g} ρ_{g} + φ S_{w} ρ_{w}) - q_{m}

（5）

由于G_g、G_w均非常小， $\frac{\partial}{\partial r} (\frac{ρ_{g} K_{r g}}{μ_{g}} G_{g})$ 和 $\frac{\partial}{\partial r} (\frac{ρ_{w} K_{r w}}{μ_{w}} G_{w})$ 项可忽略，式（5）可变为：

\frac{1}{r} \frac{\partial}{\partial r} [r K (\frac{ρ_{g} K_{r g}}{μ_{g}} + \frac{ρ_{w} K_{r w}}{μ_{w}}) \frac{\partial P}{\partial r}] - \frac{1}{r} K (\frac{ρ_{g} K_{r g}}{μ_{g}} G_{g} + \frac{ρ_{w} K_{r w}}{μ_{w}} G_{w}) = \frac{\partial}{\partial t} (φ S_{g} ρ_{g} + φ S_{w} ρ_{w}) - q_{m}

（6）

方程右边q_m项的计算式为^［14］：

q_{m} = - \frac{ρ_{g}}{B_{g}} C_{d} φ \frac{\partial P}{\partial t}

（7）

C_{d} = \frac{P_{s c} Z T V_{m} b ρ_{B}}{P Z_{s c} T_{s c} φ {(1 + b P)}^{2}}

（8）

式中：V_m为Langmuir等温吸附方程的体积常数，cm³/g；b为Langmuir等温吸附方程的压力常数，MPa^-1；ρ_B为煤岩基质块密度，g/cm³。

1.2.3　数学模型的定解条件

内边界条件：

\begin{array}{l} \frac{q}{2 π r h} = [K (\frac{K_{r g} ρ_{g}}{μ_{g}} + \frac{K_{r w} ρ_{w}}{μ_{w}}) \frac{\partial P}{\partial r} - \\ {K (\frac{K_{r g} ρ_{g}}{μ_{g}} G_{g} + \frac{K_{r w} ρ_{w}}{μ_{w}} G_{w})]}_{r = r_{w}} \end{array}

（9）

无限大外边界条件：

P (r \to \infty, t) = P_{i}

（10）

初始条件：

P (r, 0) = P_{i}

（11）

式中：q为气水总质量流量，g/s；P_i为原始地层压力，MPa。

1.3　定义气水两相拟压力和拟压力梯度

参考文献［15］定义气水两相拟压力函数为：

\begin{array}{l} F = \int_{P_{w}}^{P} K (\frac{ρ_{g} K_{r g}}{μ_{g}} + \frac{ρ_{w} K_{r w}}{μ_{w}}) d P, \\ 令 M_{p} = K (\frac{ρ_{g} K_{r g}}{μ_{g}} + \frac{ρ_{w} K_{r w}}{μ_{w}}) \end{array}

（12）

G = K (\frac{ρ_{g} K_{r g}}{μ_{g}} G_{g} + \frac{ρ_{w} K_{r w}}{μ_{w}} G_{w})

（13）

式中：F为气水两相拟压力，g/（m·s）；G为拟压力梯度，g/（m²·s）。

将式（6）左右两边分别变形，并代入式（7）、式（12）、式（13），得到气水两相渗流控制方程为：

\frac{1}{r} \frac{\partial}{\partial r} [r \frac{\partial F}{\partial r}] - \frac{G}{r} = \frac{φ C_{t}}{M_{p}} \frac{\partial F}{\partial t}

（14）

式中： $C_{t} = C_{p} + \frac{ρ_{g}}{B_{g}} C_{d}$ ，C_t表示综合压缩系数；其中，

C_{p} = C_{f} (S_{g} ρ_{g} + S_{w} ρ_{w}) + S_{g} ρ_{g} C_{g} + S_{w} ρ_{w} C_{w} + (ρ_{g} - ρ_{w}) \frac{\partial S_{g}}{\partial P}

C_f为煤层压缩系数， $C_{f} = \frac{\partial φ}{φ \partial p}$ ； $S_{g} + S_{w} = 1$ 。

带有拟压力的各定解条件

内边界条件：

\frac{q}{2 π h} = r {(\frac{\partial F}{\partial r} - G)}_{r = r_{w}}

（15）

无限大外边界条件：

F (r \to \infty, t) = F_{i}

（16）

初始条件：

F (r, 0) = F_{i}

（17）

1.4　考虑储层污染的控制方程无量纲化

当近井地带受到外来流体污染或者进行了压裂等增产措施后，储层渗透率与原状地层会有所差别，差别程度采用表皮系数S_k表示。储层受到污染可理解为在污染带产生了附加阻力，可以将该附加阻力等效为流体流动距离的改变，即井径发生变化，定义有效井径： $r_{s w} = r_{w} e^{- S_{k}}$ 。其中，r_sw为有效井径，cm；S_k为表皮系数，无量纲。为后续计算方便，定义无量纲变量：

F_{D} = \frac{2 π h}{q} (F_{i} - F)

，

G_{D} = \frac{2 π h r_{w}}{q} G

r_{s D} = \frac{r}{r_{s w}} = \frac{r}{r_{w} e^{- S_{k}}}

，

t_{s D} = \frac{M_{p}}{φ C_{t} {r_{w}}^{2}} t

式中：下角标D为无量纲化；F_i对应原始地层拟压力，g/（m·s）。

因而，式（14）—式（17）经过无量纲化后变为：

\frac{\partial^{2} F_{D}}{\partial {r_{s D}}^{2}} + \frac{1}{r_{s D}} \frac{\partial F_{D}}{\partial r_{s D}} + \frac{1}{e^{S_{k}}} \frac{G_{D}}{r_{s D}} = \frac{1}{e^{2 S_{k}}} \frac{\partial F_{D}}{\partial t_{s D}}

（18）

无量纲边界条件：

内边界条件：

\frac{- 1 - G_{D}}{e^{S_{k}}} = {\frac{\partial F_{D}}{\partial r_{s D}}}_{r_{s D} = 1}

（19）

无限大外边界条件：

F_{D} (\infty, t_{D}) = 0

（20）

初始条件：

F_{D} (r_{s D}, 0) = 0

（21）

1.5　方程拉普拉斯变换

式（18）—（21）对 $t_{D}$ 做拉普拉斯变换为：

\frac{\partial^{2} {\bar{F}}_{D}}{\partial {r_{s D}}^{2}} + \frac{1}{r_{s D}} \frac{\partial {\bar{F}}_{D}}{\partial r_{s D}} + \frac{1}{e^{S_{k}}} \frac{G_{D}}{s r_{s D}} = \frac{s}{e^{2 S_{k}}} {\bar{F}}_{D}

（22）

拉普拉斯边界条件：

内边界条件：

- \frac{1 + G_{D}}{s e^{S_{k}}} = {\frac{\partial {\bar{F}}_{D}}{\partial r_{s D}}}_{r_{s D} = 1}

（23）

无限大外边界条件：

{\bar{F}}_{D} (r_{D} \to \infty, s) = 0

（24）

初始条件：

\bar{F_{D}} (r_{D}, 0) = 0

（25）

1.6　求解拉普拉斯空间解

式（22）的形式为非齐次贝塞尔函数，其通解为式（26）：

{\bar{F}}_{D} (r_{s D}, s) = A I_{0} (r_{s D} \sqrt[]{s / e^{2 S_{k}}}) + B K_{0} (r_{s D} \sqrt[]{s / e^{2 S_{k}}}) + \int_{1}^{\infty} G (r_{s D}, τ) d τ

（26）

式中：s为拉普拉斯变量； $I_{0} (r_{s D} \sqrt[]{s / e^{2 S_{k}}})$ 和 $K_{0} (r_{s D} \sqrt[]{s / e^{2 S_{k}}})$ 分别为第一类修正的零阶贝塞尔函数和第二类修正的零阶贝塞尔函数； $G (r_{s D}, τ)$ 为格林函数。

G (r_{s D}, τ) = \{\begin{array}{l} \frac{G_{D}}{e^{S_{k}} s} K_{0} (r_{s D} \sqrt[]{s / e^{2 S_{k}}}) I_{0} (τ \sqrt[]{s / e^{2 S_{k}}}) \\ \frac{G_{D}}{e^{S_{k}} s} K_{0} (τ \sqrt[]{s / e^{2 S_{k}}}) I_{0} (r_{s D} \sqrt[]{s / e^{2 S_{k}}}) \end{array}

\begin{array}{l} (1 < τ < r_{s D}) \\ (r_{s D} < τ < \infty) \end{array}

（27）

由无限大外边界条件式（24）可知，要在无限大处使得方程值为0，则需使A=0；因此，式（26）变为：

\begin{array}{l} {\bar{F}}_{D} (r_{s D}, s) = B K_{0} (r_{s D} \sqrt[]{s / e^{2 S_{k}}}) + \\ \int_{1}^{r_{s D}} \frac{G_{D}}{e^{S_{k}} s} K_{0} (r_{s D} \sqrt[]{s / e^{2 S_{k}}}) I_{0} (τ \sqrt[]{s / e^{2 S_{k}}}) d τ \\ + \int_{r_{s D}}^{\infty} \frac{G_{D}}{e^{S_{k}} s} K_{0} (τ \sqrt[]{s / e^{2 S_{k}}}) I_{0} (r_{s D} \sqrt[]{s / e^{2 S_{k}}}) d τ \end{array}

（28）

根据内边界条件，对式（28）关于 $r_{s D}$ 求偏导，并使 $r_{s D} = 1$ ，得：

{\frac{\partial {\bar{F}}_{D} (r_{s D}, s)}{\partial r_{s D}}}_{r_{s D} = 1} = - B \sqrt[]{s / e^{2 S_{k}}} K_{1} (\sqrt[]{s / e^{2 S_{k}}}) + \frac{G_{D}}{e^{2 S_{k}} \sqrt[]{s}} I_{1} (\sqrt[]{s / e^{2 S_{k}}}) \int_{1}^{\infty} K_{0} (τ \sqrt[]{s / e^{2 S_{k}}}) d τ

（29）

其中：

\int_{1}^{\infty} K_{0} (τ \sqrt[]{s / e^{2 S_{k}}}) d τ = \int_{0}^{\infty} K_{0} (τ \sqrt[]{s / e^{2 S_{k}}}) d τ - \int_{0}^{1} K_{0} (τ \sqrt[]{s / e^{2 S_{k}}}) d τ = \frac{π}{2 \sqrt[]{s / e^{2 S_{k}}}} - \int_{0}^{1} K_{0} (τ \sqrt[]{s / e^{2 S_{k}}}) d τ

由于 τ∈［0，1］，被积函数也很小，所以这项可以忽略。因此，式（29）变为：

{\frac{\partial {\bar{F}}_{D} (r_{s D}, s)}{\partial r_{s D}}}_{r_{s D} = 1} = - B \sqrt[]{s / e^{2 S_{k}}} K_{1} (\sqrt[]{s / e^{2 S_{k}}}) + \frac{π G_{D}}{2 e^{S_{k}} s} I_{1} (\sqrt[]{s / e^{2 S_{k}}}) = - \frac{1 + G_{D}}{e^{S_{k}} s}

因此，

B = \frac{π G_{D} I_{1} (\sqrt[]{s / e^{2 S_{k}}}) + 2 (1 + G_{D})}{2 s \sqrt[]{s} K_{1} (\sqrt[]{s / e^{2 S_{k}}})}

（30）

将式（30）代入式（28），并取 $r_{s D} = 1$ ，得到无限大外边界地层井壁处无因次拟压力的拉普拉斯空间解，即：

\begin{array}{l} {\bar{F}}_{w D} (s) = \frac{π G_{D} I_{1} (\sqrt[]{s / e^{2 S_{k}}}) + 2 (1 + G_{D})}{2 s \sqrt[]{s} K_{1} (\sqrt[]{s / e^{2 S_{k}}})} K_{0} (\sqrt[]{s / e^{2 S_{k}}}) + \\ \frac{π G_{D} I_{0} (\sqrt[]{s / e^{2 S_{k}}})}{2 s \sqrt[]{s}} \end{array}

（31）

1.7　实空间解析

本文采用Laplace Stehfest反演算法^［16］，得到实空间的压力分布关系。其计算公式为：

\begin{array}{l} F_{w D} (t_{D}) = \frac{L n 2}{t_{D}} \sum_{n = 1}^{N} V_{n} {\bar{F}}_{w D} (s) \\ V_{n} = {(- 1)}^{\frac{N}{2} + n} \sum_{k = [\frac{1 + n}{2}]}^{m i n (\frac{N}{2}, n)} \frac{k^{\frac{N}{2}} (2 k)!}{(\frac{N}{2} - k)! k! (k - 1)! (n - k)! (2 k - n)!} \end{array}

\begin{array}{l} N = 10 \\ s = \frac{L n 2}{t_{D}} n \end{array}

（32）

求解过程中，首先通过Stehfest算法反演得到多组离散的实空间无量纲时间、无量纲启动压力等条件下的拟压力值，而后拟合无量纲拟压力值与无量纲时间等变量的函数关系式，代入各无量纲参数，进一步求解得到实空间下井底压力与时间、启动压力梯度等参数的函数关系。

拉普拉斯空间解表达式中包含了无量纲启动压力G_D、表皮系数S_k、无量纲时间 $t_{D}$ 3个变量，每个变量又都包含了多个参数。在数值反演过程中，对G_D依次取值0.000 1、0.000 5、0.001、0.003、0.005、0.008、0.01、0.03、0.05、0.08、0.1，对 $t_{D}$ 依次取值为1、2、3、4、5、6、7、8、9、10，对S_k分别取值为-1.5、-1、0、1、2、4、5；反演得到3个变量一一组合下的 $F_{w D}$ 值。上述取值范围参考了文献［17-21］，分别代表了多个煤层气地层的参数范围，因而适用范围广，具有较好的科学性。

拟合反演的离散数据，得到 $F_{w D}$ 与G_D、S_k和 $t_{D}$ 的方程关系式：

L n (F_{w D}) = P_{1} * L n (G_{D}) + P_{2} * e x p (P_{3} * S_{k}) + P_{4} * L n (t_{D}) + P_{5}

（33）

P₁=0.757，P₂=5.145，P₃=0.245，P₄=0.239，

P₅=-2.033，R² =0.973。

式（33）中：

F_{w D} = \frac{2 π h}{q} (F_{i} - F_{w})

（34）

G_{D} = \frac{2 π h r_{w} K}{q} * (\frac{ρ_{g} K_{r g}}{μ_{g}} G_{g} + \frac{ρ_{w} K_{r w}}{μ_{w}} G_{w})

（35）

t_{D} = \frac{M_{p}}{φ C_{t} {r_{w}}^{2}} t = \frac{K (ρ_{g} K_{r g} μ_{w} + ρ_{w} K_{r w} μ_{g})}{φ C_{t} {r_{w}}^{2} μ_{g} μ_{w}} t

（36）

其中：

K = K_{i} e^{[- a_{k} (P_{i} - P_{w})]}

（37）

ρ_{g} = \frac{ρ_{g s c}}{B_{g}} = \frac{ρ_{g s c} Z_{s c} T_{s c} p_{w}}{p_{s c} Z T}

（38）

K_{r g} = (1 - \frac{1 - S_{g} - S_{w c}}{1 - S_{w c}}) \times \sqrt[]{1 - {(\frac{1 - S_{g} - S_{w c}}{1 - S_{w c}})}^{\frac{1}{4}} \times {(1 - S_{g} - S_{w c})}^{\frac{1}{2}}}

（39）

K_{r w} = {(1 - S_{g})}^{3} \times {(\frac{1 - S_{g} - S_{w c}}{1 - S_{w c}})}^{\frac{3}{2}}

（40）

式（37）—式（40）中：K_i为原始渗透率，10^-3μm²；a_k为应力敏感系数，MPa^-1；P_w为井底压力，MPa；ρ_gsc为标况下气体密度，g/cm³；T为温度，K；Z为气体压缩因子，无量纲；S_wc为束缚水饱和度，%；S_g为含气饱和度，%^［18］。

气体黏度采用文献［19］的计算方法：

\{\begin{array}{l} μ_{g} = 10^{- 4} E e x p (X {ρ_{g}}^{Y}) \\ E = \frac{(9.379 + 0.016 07 M_{w}) {(1.8 T)}^{1.5}}{209.2 + 19.26 M_{w} + 1.8 T} \\ X = 3.448 + \frac{986.4}{1.8 T} + 0.010 09 M_{w} \\ Y = 2.447 - 0.222 4 X \end{array}

（41）

式（41）中：ρ_g表示气体密度，g/cm³；M_w表示气体分子量；μ_g表示气体黏度，mPa·s。在文献［20］中，含气饱和度与压力、渗透率有如下关系式：

S_{g} = a_{1} * L n p_{w} + a_{2} * L n K + a_{3}

（42）

式中：a₁、a₂、a₃为常数，与实验对象的渗透率有关，见表1。

表1 不同渗透率储层的a₁、a₂、a₃值

Table 1 a₁, a₂and a₃ values of reservoirs with different permeability

渗透率/（10^-3μm²）	a₁	a₂	a₃
K≥50	3	1.8	45
K=10~50	3.5	2	40
K=1~10	4.5	3	35
K=0.5~1	5	2	33
K=0.1~0.5	5	2	25
K≤0.1	7	2	15

新窗口打开| 下载CSV

结合式（37）和式（42）可得：

S_{g} = a_{1} \times L n P_{w} - a_{2} a_{k} (P_{i} - P_{w}) + a_{2} \times L n K_{i} + a_{3}

（43）

含气饱和度对压力的导数为：

\frac{\partial S_{g}}{\partial P} = \frac{a_{1}}{P_{w}} + a_{2} a_{k}

（44）

将式（44）代入C_p的计算式，变为：

C_{p} = S_{g} [ρ_{g} C_{g} - ρ_{w} C_{w} + c_{f} (ρ_{g} - ρ_{w})] + ρ_{w} (C_{w} + C_{f}) + (ρ_{g} - ρ_{w}) (\frac{a_{1}}{P_{w}} + a_{2} a_{k})

因此，C_t的计算公式变为：

\begin{array}{l} C_{t} = C_{p} + \frac{ρ_{g}}{B_{g}} C_{d} = S_{g} [ρ_{g} C_{g} - ρ_{w} C_{w} + C_{f} (ρ_{g} - ρ_{w})] \\ + ρ_{w} (C_{w} + C_{f}) + (ρ_{g} - ρ_{w}) (\frac{a_{1}}{P_{w}} + a_{2} a_{k}) + \\ \frac{{ρ_{g}}^{2}}{ρ_{g s c}} \frac{P_{s c} Z T V_{m} b ρ_{B}}{P_{w} Z_{s c} T_{s c} φ {(1 + b P_{w})}^{2}} \end{array}

（45）

工程中，采用无需迭代计算的Papay法计算Z值，即：

\{\begin{array}{l} Z = 1 - \frac{3.52 p_{r}}{10^{0.918 3 T_{r}}} + \frac{0.274 {p_{r}}^{2}}{10^{0.817 5 T_{r}}} \\ p_{r} = \frac{P_{w}}{p_{c}}, T_{r} = \frac{T}{T_{c}}, \\ T_{c} = a_{0} + a_{1} δ_{n g}, p_{c} = b_{0} + b_{1} δ_{n g} \end{array}

（46）

式中：p_r为天然气对比压力，无量纲； p_c为天然气视临界压力，MPa；T_r为天然气对比温度，无量纲；T_c 为天然气视临界温度，K；δ_ng为天然气相对密度，煤层气主要为甲烷，取0.55。由此， a₀=106；a₁=152.22；b₀=4 778；b₁=-248.21。

煤层气在开发中，受应力敏感效应，渗透率和孔隙度均发生变化，二者可采用火柴棍模型建立关系，即：

\frac{K}{K_{i}} = {(\frac{ϕ}{ϕ_{i}})}^{3}

（47）

式中： $ϕ_{i}$ 为初始孔隙度，%。

将式（34）—式（36）代入式（33）中得到式（48），

\begin{array}{l} L n (\frac{2 π h}{q} \int_{P_{w}}^{P_{i}} K (\frac{ρ_{g} K_{r g}}{μ_{g}} + \frac{ρ_{w} K_{r w}}{μ_{w}}) d P) = \\ P_{1} \times L n (\frac{2 π h r_{w}}{q} K (\frac{ρ_{g} K_{r g}}{μ_{g}} G_{g} + \frac{ρ_{w} K_{r w}}{μ_{w}} G_{w})) + \\ P_{2} \times e x p (P_{3} \times S_{k}) + P_{4} \times L n (\frac{K (ρ_{g} K_{r g} μ_{w} + ρ_{w} K_{r w} μ_{g})}{φ C_{t} {r_{w}}^{2} μ_{g} μ_{w}} t) + P_{5} \end{array}

（48）

式（48）的左边为复杂的积分表达式，右边为复杂的非线性关系式，难以得到精确解析解。同时，参数K、ρ_g、K_rg、C_t、μ_g等又是变量P_w（P_w随时间t变化）的函数，且同样是复杂的非线性关系式。因而，无法进行解析计算。

记方程左边为L（P_w），右边为R（P_w）；参考文献［17-21］相关参数的取值，对式（48）中的表皮系数S_k取值为-4、-3、-2、-1、0、1、2、3、4，应力敏感系数a_k按照间隔0.001 MPa^-1、从0.001到0.005 MPa^-1，气水总质量流量q按照间隔20 g/s、从100到240 g/s，井底压力P_w按照间隔1.25 MPa、从3.75到15 MPa，气体启动压力梯度G_g按照间隔0.000 5 MPa/m、从0.000 5到0.004 MPa/m，水的启动压力梯度G_w按照间隔0.005 MPa/m、从0.005到0.04 MPa/m。将上述6个变量进行完全组合后，对左边采用复化梯形数值积分法计算每一个组合对应的L（P_w）值，并将L（P_w）值作为已知量与R（P_w）的常数项合并，形成以时间t为未知量的方程。

在实际应用时，除了上述变量，还需要给定一些常量参数，如地层厚度h，因此需要一个既包含上述变量，又包含常量的参数，发现C_t符合该特点。所以，在拟合的方程中加入参数C_t。

按照上述方法，得到关系式（49）：

P_{w} = c_{1} \times S_{k} + c_{2} \times a_{k} + c_{3} \times q + c_{4} \times G_{g} + c_{5} \times G_{w} + c_{6} \times {C_{t}}^{c_{7}} + c_{8} \times L g t + c_{9}

（49）

c₁=-5.692，c₂=-8657.083，c₃=-0.087，c₄=-6.27，c₅=-1.655，c₆=61.066，c₇=-0.559，c₈=-15.08，c₉=-224.268。R²=0.970 3。

式（49）建立了井底压力与表皮系数、应力敏感系数、气水总产量、气体和水的启动压力梯度、综合压缩系数、生产时间的显式关系式。关系式相关系数超过0.97。从式（49）看出，井底压力与综合压缩系数是幂函数关系、与时间是对数关系、与其他参数是线性关系。同时，除了综合压缩系数外，其他参数的系数都与井底压力P_w负相关。该结论与实际生产规律相符，实际使用时，代入相关参数便能直接求得井底压力。

本文在连续方程中加入了质量源q_m项，符合煤层气不断解吸产生新气源的情况；现有研究只截止到了无因次拟压力与无因次时间及各影响因素的关系，即式（32），而从式（34）—式（47）可见，式（32）中的参数又包含了复杂的计算公式，因此，仅从式（32）还不能直接评价井底压力与产量、时间、表皮系数等参数的关系；而本文通过公式推导、2次拟合等过程，最终得到能够直接数值计算的井底压力关系式。首先是利用多组实际生产中的数据，第一次拟合得到 $F_{w D}$ 与、S_k和 $t_{D}$ 的关系式（33）；将式（34）—式（47）代入拟合的关系式，得到了一个非常复杂的非线性关系式（48），其左边是积分表达式，而且被积函数同样非常复杂，无法获得解析解，因此，通过变量赋值方法，先对左边进行复化梯形数值积分，得到多个离散值，将每个离散值分别与公式右边合并，获得多组离散值，将该多组离散值拟合获得最终的式（49）。后面的2次拟合以及求解复杂关系式的过程是本文主要的创新之处。

2 模型应用及评价

2.1　模型应用

文献［21］描述了沁南东—夏店区块五阳1-103井的实际产量、动液面等情况，为现场实际资料。本文利用该资料评价模型的准确性。五阳1-103井是布置在沁南东—夏店区块构造带上的一口生产井，研究区内主要褶曲面积和幅度一般比较小，呈长轴线型褶皱，褶曲走向与整个沁水盆地向斜轴向近于一致。研究区内断层发育，北东向的正断层发育规模较大，而近南北方向断层发育规模相对较小。3^#煤层为主力采气层，采样点煤层约4.5 m厚，仅在煤层中部有0.5 m厚的原生结构煤分层，构造煤破坏程度较高，普遍为碎粒—糜棱构造煤。采样点煤层埋深约500 m，根据附近煤层气井试井资料，可知储层压力约为5 MPa。五阳1-103井的地层参数见表2。

表2 五阳1-103井的基本参数

Table 2 Basic parameters of Well Wuyang 1-103

埋深

层厚

含气量

/（m³/t）

兰氏体积

/（m³/t）

兰氏压力

/MPa

原始储层压力

/MPa

临界解吸压力

/MPa

煤层密度

/（g/cm³）

原始渗透率

/（10^-3μm²）

储层温度

原始孔隙度

650

6.1

1.8

4.5

1.48

1.4

0.085

297

2.5

井径

/cm

井控半径

表皮系数

吸附常量

/MPa^-1

泊松比

煤层压缩系数

/MPa^-1

气体压缩系数

/MPa^-1

地层水压缩系数

/MPa^-1

束缚水饱和度

压力敏感系数

/MPa^-1

排水降压速度

/（MPa/d）

150

-1

0.56

0.3

0.000 22

0.01

0.000 44

0.001

0.026 8

新窗口打开| 下载CSV

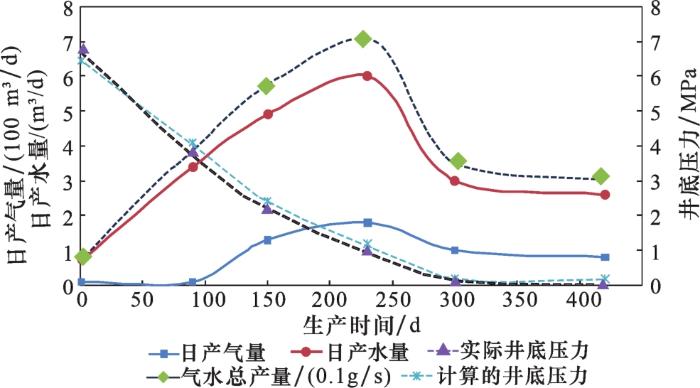
该井采用均匀降压的方式进行初期生产，130 d内动液面下降350 m，排水降压速度0.026 8 MPa/d。平均日产气量103 m³/d，生产220 d达到峰值产量195 m³/d；300 d后动液面稳定维持在800 m左右，进入稳产期，日产气量80~100 m³，整个排采期，产水量一直较大。将该井参数代入本文模型计算井底压力，再将实际的产量、动液面换算的实际井底压力绘制到同一张图中，如图1所示。由于各产量数值差异较大，因此将单位进行了调整。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 五阳1-103井实际生产资料与计算值对比

Fig.1 Comparison between actual production data and calculated value of Well Wuyang 1-103

图1描述了气和水的日产量以及井底压力随时间的变化关系，并将计算的井底压力与实际井底压力进行了比较，以验证本文模型的准确性。从图1可见，五阳1-103井刚开始生产时，井底压力为6.8 MPa，高于原始储层压力4.5 MPa，表明井筒内存有大量积液；生产后日产水量逐渐增大，直到约3个月后开始产气，在230~250 d，气水产量均达到最大，之后开始下降，350 d左右趋于稳定。在此过程中，井底压力逐渐降低，在气水产量达到峰值时，井底压力仍没有降到最低，在300 d左右时逐渐稳定，最后低于0.1 MPa，说明地层产出水被及时排出井筒，井底接近无积液状态。另外，从最初的生产阶段到稳定阶段，本文模型计算的井底压力与实际井底压力均较为接近，最高符合率达到94.76%，最低符合率也达到82.3%。产量变化过程，也与上述实际工况符合。

2.2　井底压力影响因素分析

在验证了模型准确性的基础上，进一步评价3个因素对井底压力的影响。评价时，保持其中2个因素不变，求得第3个因素对井底压力的影响规律。仍以五阳1-103井为评价基础，所在煤层气藏的基本参数为：T=300 K，K_i=0.085×10^-3μm²，ρ_w=1.0 g/cm³，P_e=4.5 MPa，φ=2.5%，C_g=0.01 MPa^-1，C_w=0.000 435 MPa^-1，C_f=0.000 22 MPa^-1，V_m=15.5 cm³/g，b=0.56 MPa^-1，ρ_B=1.4 g/cm³。

2.2.1　表皮系数

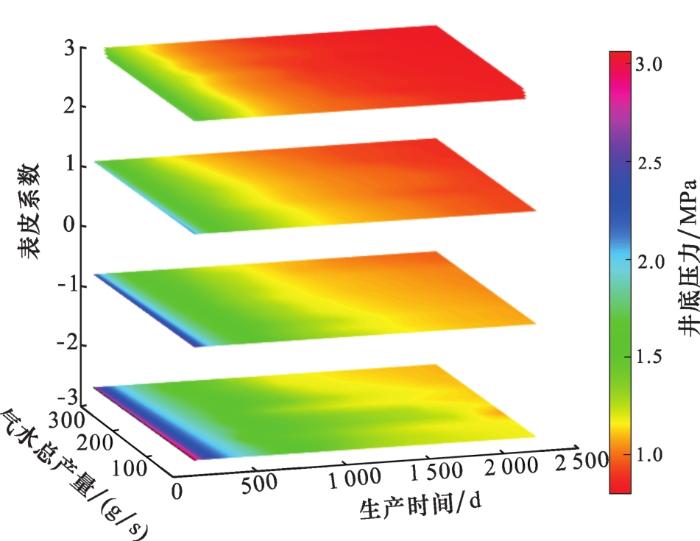
保持基本参数不变，取G_g = 0.000 5 MPa/m，G_w=0.005 MPa/m，a_k=0.001 MPa^-1，S_k=-3、-1、1、3，得到以时间t、产量q=10~300 g/s、表皮系数S_k为自变量，以井底压力P_w为因变量的关系图，如图2所示。在图2中，自变量有3个，由于无法显示四维图，因此，井底压力P_w通过颜色变化表示，见图2中右侧颜色条，下同。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 产量、表皮系数、时间与井底压力关系

Fig.2 Relationship between production， skin factor， time and BHP

在图2中，4个水平四边形图分别对应不同S_k值。随着S_k值的增大，浅红色区域逐渐增多，绿色区域逐渐减少，代表着P_w值整体减小；当S_k=-3时，还存在蓝色和深红色区域，而当S_k= 3时，蓝色部分完全消失。颜色波动范围大，表明S_k对井底压力影响较大。该变化过程表明，在其他条件不变时，S_k越小，表示地层渗流能力较好，地层流体更容易流入井底，原始地层压力损耗较小，则井底压力相对更高。

对于同一S_k值，无论是表示高P_w值的蓝色条带还是相对较低的绿色条带，随着产量q增加，都呈现出由宽变窄的趋势，即产量增加，井底压力降低，这与实际生产过程中通过增加压差来提高产量的过程相符。

为了更加清晰地展现井底压力随时间的变化，针对同一S_k值，选取数个变化明显的代表性点，给出井底压力与时间关系图（图3）。以S_k=-3为例，在生产了30 d、60 d、240 d时，P_w值分别为3.06 MPa、2.58 MPa和1.97 MPa，之后开始缓慢下降，直到生产了1 200 d时仅下降了0.67 MPa，之后稳定在1.20 MPa附近。表明随着时间t增加，P_w值先较快地减小，然后逐渐缓慢降低，直到趋于稳定。该变化过程与验证井的生产工况较为相符。刚开始排液过程中，井底压力快速降低至地层压力附近，地层开始产水，由于地层渗透率较低，产水量较少，井底压力继续缓慢降低，同时，地层压力降不断向地层边界传播，当压力降低到解吸压力以下后开始产气，此时，地层产水量已经较小，井底压力趋于稳定。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 井底压力随时间变化趋势

Fig.3 BHP change with time to some specified values

为了更清楚地显示BHP在图2、图4和图5中随时间的变化规律，从各图中分别选取了数个代表值得到图3，其中，G_w和G_g的BHP值相近，以G_w为代表。

图4

新窗口打开| 下载原图ZIP| 生成PPT

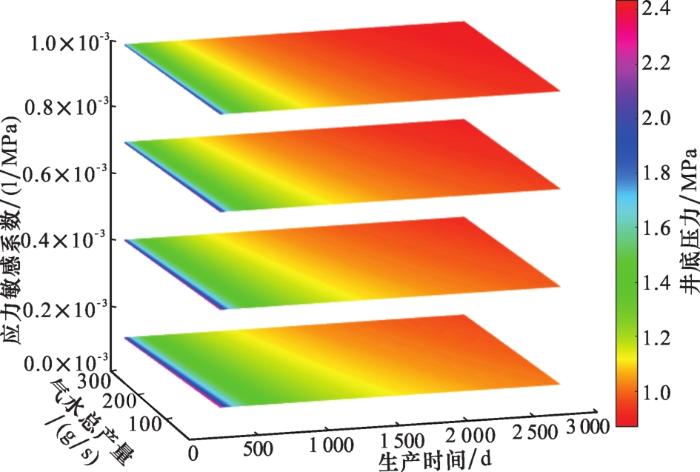
图4 产量、应力敏感、时间与井底压力关系

Fig.4 Relationship between production， stress sensitivity， time and BHP

图5

新窗口打开| 下载原图ZIP| 生成PPT

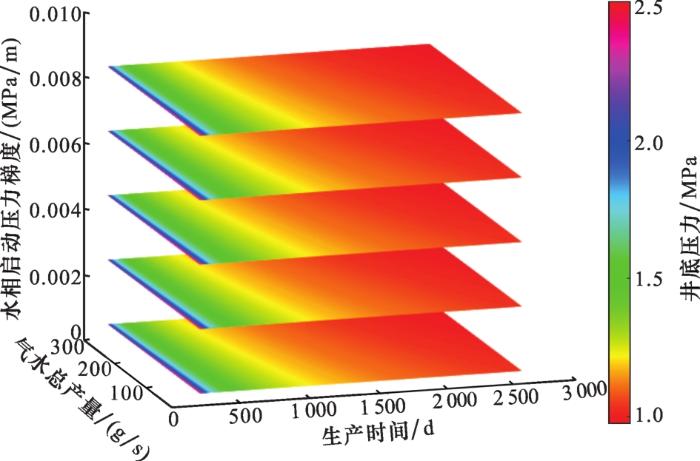
图5 产量、水的启动压力梯度、时间与井底压力关系

Fig.5 Relationship between production， water start-up pressure gradient， time and BHP

2.2.2　应力敏感性

保持基本参数不变，取S_k=1，G_g=0.000 5 MPa/m，G_w=0.005 MPa/m，a_k=0.001、0.004、0.007、0.01 MPa^-1，得到以产量q=10~300 g/s、时间t、应力敏感系数a_k为自变量，以井底压力P_w为因变量的关系图，如图4所示。

从图4中可见，随着a_k值增大，浅红色区域逐渐增多，绿色和深蓝色区域逐渐减少，代表着P_w值整体减小，表明a_k对井底压力影响较大。该变化过程表明，在其他条件不变时，a_k值越大，则地层的应力敏感性越强；同样的地层压力下降值，强应力敏感性地层渗透率会降低更多，流体的渗流阻力增加更多，导致井壁处剩余的压力，即井底压力越小。

对于同一a_k值，随着产量q增加，浅红色条带由窄变宽，而表示较高P_w的条带相应变窄，即随产量增加，井底压力逐渐降低，这与实际生产过程也完全相符。

同理，以a_k=0.001 MPa^-1为例，在生产了30 d时，P_w值为2.44 MPa，60 d时快速降为2.07 MPa，而从150~1 200 d之间只降低了约0.53 MPa，之后在1.02 MPa附近波动，如图3所示。表明随着时间t增加，P_w值先快速减小，再缓慢降低，直至趋于稳定。该变化过程同样与验证井的生产特征相符。刚开始排液过程中，井底压力快速降低至地层压力附近，井底积液减少，地层开始产水，由于渗透率较低且生产压差较小，产水量较少，使得井底压力继续缓慢降低；当压力降低到解吸压力以下后开始产气，此时，地层产水量已经较小，井底压力变化趋于稳定。

2.2.3　启动压力梯度

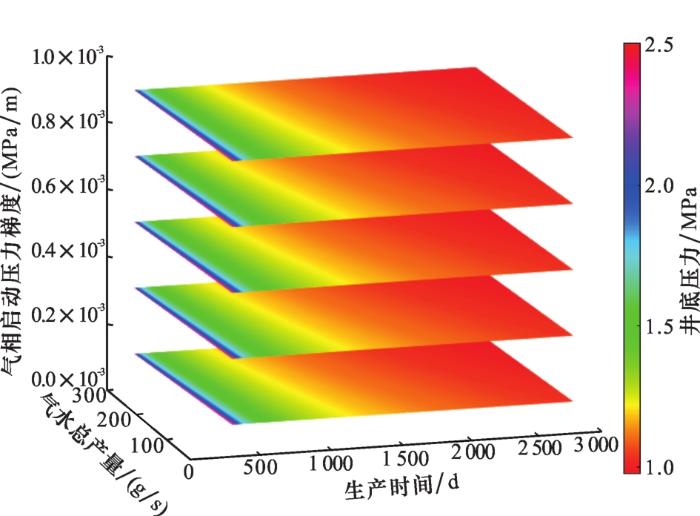
保持基本参数不变，取S_k =1，a_k=0.001 MPa^-1，G_g和G_w分别取G_g=0.000 5、0.002 5、0.004 5、0.006 5、0.008 5 MPa/m，G_w=0.005、0.025、0.045、0.065、0.085 MPa/m，得到以产量q=10~300 g/s、时间t、气体启动压力梯度G_g或水的启动压力梯度G_w为自变量，以井底压力P_w为因变量的关系图，如图5、图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 产量、气相启动压力梯度、时间与井底压力关系

Fig.6 Relationship between production， gas start-up pressure gradient， time and BHP

从图5和图6中可见，水相启动压力梯度与气体启动压力梯度的变化趋势非常接近，表明二者对井底压力的影响类似，下文以水相启动压力梯度图为例进行说明。图5中有5个水平四边形图，分别对应不同G_w值。

随着G_w值增大，各图的颜色分布变化不大，表明启动压力梯度对最终井底压力值影响较小。分析原因是，启动压力梯度代表了流体在一定压差下是否能够流动，间接表示了渗透率大小，即渗流能力的高低；因此，在一定的范围内，只要发生了流体流动，压力总能传递到井底，使得最终的井底压力将无较大差异。

对于同一G_w值，随着产量增加，蓝色条带和绿色条带都逐渐变窄，即产量增加，井底压力降低，这与实际生产过程也完全相符。随着时间t增加，P_w值也逐渐减小，直至趋于稳定。同理，以G_w = 0.005 MPa/m为例，在生产了30 d、60 d和150 d时，P_w值分别为2.51 MPa、2.12 MPa和1.73 MPa，之后缓慢下降，当生产了1 200 d时下降到1.18 MPa，如图3所示。另外，低产量（50 g/s）生产时，井底压力在1 200 d左右达到稳定，而在280 g/s的较高产量生产时，500 d左右即达到稳定。

从图2—图6可见，3个因素对井底压力均有不同程度影响。相对于另外2个因素，表皮系数变化导致的井底压力波动更加剧烈，从该角度判断，表皮系数的影响最大，其次是应力敏感，再次是启动压力梯度。因此，从煤层气藏生产角度，在前期的钻完井过程中，需要最大程度减少储层污染；在开发中减小排液速度，防止压差过大造成应力敏感而降低渗流能力，甚至增加启动压力梯度。

3 结论

（1）本文在传统拟压力函数与影响因素关系基础上，通过对无因次拟压力和时间的分解、二次拟合，建立了实际井底压力与时间、应力敏感系数、表皮系数、总产量、启动压力梯度的显式关系式；通过多组现场资料验证，从初始生产阶段到压力稳定阶段，模型准确率达到82.3%~94.76%。只需将相关参数代入本文模型，便能直接求得井底压力，应用简单，克服了传统拟压力隐函数需要数值求解的不足，还可直接用于动态渗透率变化等进一步的研究工作。

（2）影响因素分析结果表明，对于低渗煤层，表皮系数对井底压力和产量影响最大，其次是应力敏感性，启动压力梯度影响最小，因此，开发前尽可能减少污染，开发中保持合理生产压差减少应力敏感伤害。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

CLARKSON C R. Case study： Production data and pressure transient analysis of horseshoe canyon CBM wells［J］.Journal of Canadian Petroleum Technology，2009，48（10）：40096-40105.

[本文引用: 1]

[2]

SEIDLE J. Fundamentals of Coalbed Methane Reservoir Engineering［M］.Tulsa： PennWell Books，2011.

[本文引用: 1]

[3]

李瑞. 煤层气排采中储层压降传递特征及其对煤层气产出的影响［D］. 北京：中国地质大学（北京）， 2017.

[本文引用: 1]

LI R. Transfer Characteristics of Reservoir Pressure Drop during Coalbed Methane Drainage and Production and Its Influence on Coalbed methane Production［D］. Beijing： China University of Geosciences（Beijing）， 2017.

[本文引用: 1]

[4]

刘新福，綦耀光，胡爱梅，等. 单相水流动煤层气井流入动态分析［J］. 岩石力学与工程学报， 2011， 30（5）： 960-966.

[本文引用: 1]

LIU X F， QI Y G， HU A M， et al. Inflow performance analysis of single-phase water flowing coalbed methane wells［J］. Journal of Rock Mechanics and Engineering， 2011，30 （5）： 960-966.

[本文引用: 1]

[5]

杨红斌，王志城，谢新秋，等.应力敏感条件下合理井底流压的判定研究［J］.科学技术与工程， 2012， 12（7）： 1492-1495.

[本文引用: 1]

YANG H B， WANG Z C， XIE X Q， et al. Study on determination of reasonable bottom hole flowing pressure under stress sensitive conditions［J］. Science Technology and Engineering， 2012，12 （7）： 1492-1495.

[本文引用: 1]

[6]

赵金，张遂安. 煤层气排采储层压降传播规律研究［J］.煤炭科学技术，2012，40（10）：65-68.

[本文引用: 1]

ZHAO J， ZHANG S A. Study on pressure drop propagation law of coalbed methane drainage reservoir［J］.Coal Science and Technology， 2012， 40 （10）： 65-68.

[本文引用: 1]

[7]

赵俊龙，汤达祯，许浩，等. 考虑孔渗变化的非稳态渗流煤储层压降传播规律［J］.科学技术与工程， 2015， 15（5）： 46-53.

[本文引用: 1]

ZHAO J L， TANG D Z， XU H， et al. Pressure drop propagation law of unsteady seepage coal reservoir considering pore permeability change［J］. Science Technology and Engineering， 2015，15 （5）： 46-53.

[本文引用: 1]

[8]

张永平，孟召平，刘贺，等. 煤层气井排采初期井底流压动态模型及应用分析［J］.煤田地质与勘探， 2016， 44（2）： 29-33.

[本文引用: 1]

ZHANG Y P， MENG Z P， LIU H， et al. Dynamic model for bottomhole flowing pressure in initial stage of CBM wells drainage and its application［J］. Coal Geology & Exploration， 2016， 44（2）： 29-33.

[本文引用: 1]

[9]

薛军，张茂林，宋惠馨，等. 考虑多因素的低渗气藏产能计算方程［J］. 科学技术与工程， 2020， 20（10）： 3940-3945 .

[本文引用: 1]

XUE J， ZHANG M L， SONG H X， et al. Productivity calculation equation of low permeability gas reservoir considering multiple factors［J］.Science Technology and Engineering，2020， 20（10）： 3940-3945.

[本文引用: 1]

[10]

朱维耀，董熇，宋洪庆，等. 低渗透煤层气水两相非线性渗流数学模型及计算分析［J］.科技导报， 2013， 31（22）： 36-39.

[本文引用: 1]

ZHU W Y， DONG G， SONG H Q， et al. Mathematical model and calculation analysis of two-phase nonlinear seepage of low permeability coalbed methane and water［J］. Science and Technology Herald， 2013，31 （22）： 36-39.

[本文引用: 1]

[11]

张先敏，同登科. 低渗透煤层气非线性流动分析［J］. 工程力学， 2010， 27（10）： 219-223.

[本文引用: 1]

ZHANG X M， TONG D K. Nonlinear flow analysis of low permeability coalbed methane［J］.Engineering Mechanics，2010，27（10）：219-223.

[本文引用: 1]

[12]

张小龙，杨志兴. 启动压力梯度对低渗气藏不稳定渗流特征的影响［J］. 油气井测试， 2018， 27（3）：7-13.

[本文引用: 1]

ZHANG X L， YANG Z X. Impacts of start-up pressure gradient on features of transient seepage low in low-permeability gas reservoirs［J］.Well Testing， 2018，27（3）：7-13.

[本文引用: 1]

[13]

ANBARCI K， ERTEKIN T. A comprehensive study of pressure transient analysis with sorption phenomena for single-phase gas flow in coal seams［C］. SPE Annual Technical Conference and Exhibition， OnePetro， 1990.

[本文引用: 1]

[14]

SUN Z， SHI J， WANG K， et al. The gas-water two phase flow behavior in low-permeability CBM reservoirs with multiple mechanisms coupling［J］.Journal of Natural Gas Science & Engineering， 2018， 26（4）： 218-229.

[本文引用: 1]

[15]

冯其红，舒成龙，张先敏，等. 煤层气井两相流阶段排采制度实时优化［J］.煤炭学报，2015，40（1）：142- 148.

[本文引用: 1]

FENG Q H， SHU C L， ZHANG X M，et al. Real-time optimization of drainage schedule for coalbed methane wells at gas-water two-phase flow stage［J］. Journal of China Coal Society，2015，40（1）：142 -148.

[本文引用: 1]

[16]

WANG H， KOU Z， GUO J， et al. A semi-analytical model for the transient pressure behaviors of a multiple fractured well in a coal seam gas reservoir［J］. Journal of Petroleum Science and Engineering， 2021， 198： 108-159.

[本文引用: 1]

[17]

林文姬，王烽，汤达祯，等. 韩城矿区煤储层非稳态渗流压降传播规律［J］.煤炭科学技术，2016，44（S1）：131-136.

[本文引用: 2]

LIN W J， WANG F， TANG Z D， et al. Propagation law of unsteady seepage pressure drop in coal reservoir in Hancheng mining area［J］. Coal Science and Technology， 2016，44 （S1）： 131-136.

[本文引用: 2]

[18]

刘文超，刘曰武. 低渗透煤层气藏中气—水两相不稳定渗流动态分析［J］.力学学报，2017，49（4）：828-835.

[本文引用: 1]

LIU W C， LIU Y W. Dynamic analysis on gas-water two-phase unsteady seepage flow in low-permeable coalbed gas reservoirs［J］. Chinese Journal of Theoretical and Applied Mechanics， 2017， 49（4）： 828-835.

[本文引用: 1]

[19]

LEE A L， GONZALEZ M H， EAKIN B E. The viscosity of natural gases［J］. Journal of Petroleum Technology，1966，18（8）： 997-1000.

[本文引用: 1]

[20]

胡勇，徐轩，李进步，等. 砂岩气藏充注含气饱和度实验研究［J］.天然气地球科学，2016，27（11）：1979-1984.

[本文引用: 1]

HU Y， XU X， LI J B， et al. Experimental study on gas saturation of sandstone gas reservoir filling［J］. Natural Gas Geoscience， 2016，27 （11）： 1979-1984.

[本文引用: 1]

[21]

许小凯. 煤层气直井排采中煤储层应力敏感性及其压降传播规律［D］. 北京：中国矿业大学（北京），2016.

[本文引用: 3]

XU X K. Stress Sensitivity and Pressure Drop Propagation Law of Coal Reservoir In Vertical Well Drainage And Production of Coalbed Methane［D］. Beijing： China University of mining and Technology （Beijing）， 2016.

[本文引用: 3]

... CLARKSON^［1］通过压力瞬变分析模型计算排采过程中平均储层压力，建立了饱和煤层气藏储层压降变化模型.SEIDLE^［2］介绍了平均储层压力动态变化数学模型和储层压降模拟方法.但平均储层压力仅反映某一阶段的整体压力大小，无法反映压力在空间上的分布情况^［3］.刘新福等^［4］以稳态渗流为前提，分别按照达西渗流和非达西渗流公式，结合表皮效应研究了煤层中水的产能与压差关系，以确定煤层气井合理的工作方式.杨红斌等^［5］在平面径向达西渗流基础上，考虑了启动压力和应力敏感因素对井底流压的影响.赵金等^［6］考虑表皮影响，根据达西定律描述了非稳态渗流下的压力分布.赵俊龙等^［7］考虑了煤储层开发过程中孔隙度和渗透率的动态变化，在平面径向非稳态达西渗流模型的基础上，研究了孔渗条件对压降传播的影响.张永平等^［8］基于达西渗流公式建立了外边界无限大、内边界分别为定产和定压条件下的井底流压动态预测模型.薛军等^［9］考虑了滑脱效应、启动压力梯度、应力敏感性、高速非达西流动及水锁损害等5个因素的稳态产能方程.朱维耀等^［10］考虑气水启动压力梯度和连续源，采用有限差分法求解方程得到两相产能变化规律.张先敏等^［11］考虑了启动压力梯度、表皮系数的煤层气非线性流动，得到了无因次井底压力与无因次时间的双对数关系图. ...

... 在文献［12］的连续性方程基础上，结合煤层气生产过程中不断解吸产生新气源的特点，增加了质量源项，见式（1）： ...

... 采用文献［13］的公式计算气水径向渗流速度，见式（2）： ...

... 方程右边q_m项的计算式为^［14］： ...

... 参考文献［15］定义气水两相拟压力函数为： ...

... 本文采用Laplace Stehfest反演算法^［16］，得到实空间的压力分布关系.其计算公式为： ...

... 拉普拉斯空间解表达式中包含了无量纲启动压力G_D、表皮系数S_k、无量纲时间

t_{D}

3个变量，每个变量又都包含了多个参数.在数值反演过程中，对G_D依次取值0.000 1、0.000 5、0.001、0.003、0.005、0.008、0.01、0.03、0.05、0.08、0.1，对

t_{D}

依次取值为1、2、3、4、5、6、7、8、9、10，对S_k分别取值为-1.5、-1、0、1、2、4、5；反演得到3个变量一一组合下的

F_{w D}

值.上述取值范围参考了文献［17-21］，分别代表了多个煤层气地层的参数范围，因而适用范围广，具有较好的科学性. ...

... 记方程左边为L（P_w），右边为R（P_w）；参考文献［17-21］相关参数的取值，对式（48）中的表皮系数S_k取值为-4、-3、-2、-1、0、1、2、3、4，应力敏感系数a_k按照间隔0.001 MPa^-1、从0.001到0.005 MPa^-1，气水总质量流量q按照间隔20 g/s、从100到240 g/s，井底压力P_w按照间隔1.25 MPa、从3.75到15 MPa，气体启动压力梯度G_g按照间隔0.000 5 MPa/m、从0.000 5到0.004 MPa/m，水的启动压力梯度G_w按照间隔0.005 MPa/m、从0.005到0.04 MPa/m.将上述6个变量进行完全组合后，对左边采用复化梯形数值积分法计算每一个组合对应的L（P_w）值，并将L（P_w）值作为已知量与R（P_w）的常数项合并，形成以时间t为未知量的方程. ...

... 拉普拉斯空间解表达式中包含了无量纲启动压力G_D、表皮系数S_k、无量纲时间

t_{D}

3个变量，每个变量又都包含了多个参数.在数值反演过程中，对G_D依次取值0.000 1、0.000 5、0.001、0.003、0.005、0.008、0.01、0.03、0.05、0.08、0.1，对

t_{D}

依次取值为1、2、3、4、5、6、7、8、9、10，对S_k分别取值为-1.5、-1、0、1、2、4、5；反演得到3个变量一一组合下的

F_{w D}

值.上述取值范围参考了文献［17-21］，分别代表了多个煤层气地层的参数范围，因而适用范围广，具有较好的科学性. ...

... 式（37）—式（40）中：K_i为原始渗透率，10^-3μm²；a_k为应力敏感系数，MPa^-1；P_w为井底压力，MPa；ρ_gsc为标况下气体密度，g/cm³；T为温度，K；Z为气体压缩因子，无量纲；S_wc为束缚水饱和度，%；S_g为含气饱和度，%^［18］. ...

... 气体黏度采用文献［19］的计算方法： ...

... 式（41）中：ρ_g表示气体密度，g/cm³；M_w表示气体分子量；μ_g表示气体黏度，mPa·s.在文献［20］中，含气饱和度与压力、渗透率有如下关系式： ...

... 拉普拉斯空间解表达式中包含了无量纲启动压力G_D、表皮系数S_k、无量纲时间

t_{D}

3个变量，每个变量又都包含了多个参数.在数值反演过程中，对G_D依次取值0.000 1、0.000 5、0.001、0.003、0.005、0.008、0.01、0.03、0.05、0.08、0.1，对

t_{D}

依次取值为1、2、3、4、5、6、7、8、9、10，对S_k分别取值为-1.5、-1、0、1、2、4、5；反演得到3个变量一一组合下的

F_{w D}

值.上述取值范围参考了文献［17-21］，分别代表了多个煤层气地层的参数范围，因而适用范围广，具有较好的科学性. ...

... 文献［21］描述了沁南东—夏店区块五阳1-103井的实际产量、动液面等情况，为现场实际资料.本文利用该资料评价模型的准确性.五阳1-103井是布置在沁南东—夏店区块构造带上的一口生产井，研究区内主要褶曲面积和幅度一般比较小，呈长轴线型褶皱，褶曲走向与整个沁水盆地向斜轴向近于一致.研究区内断层发育，北东向的正断层发育规模较大，而近南北方向断层发育规模相对较小.3^#煤层为主力采气层，采样点煤层约4.5 m厚，仅在煤层中部有0.5 m厚的原生结构煤分层，构造煤破坏程度较高，普遍为碎粒—糜棱构造煤.采样点煤层埋深约500 m，根据附近煤层气井试井资料，可知储层压力约为5 MPa.五阳1-103井的地层参数见表2. ...

... 拉普拉斯空间解表达式中包含了无量纲启动压力G_D、表皮系数S_k、无量纲时间

t_{D}

3个变量，每个变量又都包含了多个参数.在数值反演过程中，对G_D依次取值0.000 1、0.000 5、0.001、0.003、0.005、0.008、0.01、0.03、0.05、0.08、0.1，对

t_{D}

依次取值为1、2、3、4、5、6、7、8、9、10，对S_k分别取值为-1.5、-1、0、1、2、4、5；反演得到3个变量一一组合下的

F_{w D}

值.上述取值范围参考了文献［17-21］，分别代表了多个煤层气地层的参数范围，因而适用范围广，具有较好的科学性. ...

〈

〉