多射孔压裂对水力裂缝扩展规律的影响

doi:10.11764/j.issn.1672-1926.2021.09.011

多射孔压裂对水力裂缝扩展规律的影响

马许平^,¹, 曾庆利¹^,²

1.中国科学院大学地球与行星科学学院，北京 100049

2.中国科学院计算地球动力学重点实验室，北京 100049

Influence of multi-perforation fracturing on the regularity of hydraulic fractures propagation

MA Xuping^,¹, ZENG Qingli¹^,²

1.College of Earth and Planetary Sciences，University of Chinese Academy of Sciences，Beijing 100049，China

2.Laboratory of Computational Geodynamics of Chinese Academy of Sciences，Beijing 100049，China

收稿日期: 2021-08-02 修回日期: 2021-09-15 网络出版日期: 2021-12-31

基金资助:

国家自然科学基金项目. 41772382. 42071020

Received: 2021-08-02 Revised: 2021-09-15 Online: 2021-12-31

作者简介 About authors

马许平（1995-），男，回族，宁夏固原人，硕士研究生，主要从事地质灾害及页岩气开发研究.E-mail：maxuping19@mails.ucas.ac.cn. , E-mail：maxuping19@mails.ucas.ac.cn

摘要

岩石水力压裂涉及到复杂的流固耦合过程，水力裂缝扩展规律及压裂液与岩体间耦合机理是目前研究的热点与难点。基于ABAQUS平台的扩展有限元法（XFEM）具有计算精度高和计算量小的优势，其中的Soil模块可用来模拟岩石水力压裂的复杂过程，分析水力裂缝的扩展路径、宽度、应力等基本参数。通过上述数值模拟方法，研究了单射孔压裂、两射孔异步压裂、两射孔同步压裂3种工况对水力裂缝扩展路径、裂缝宽度、裂缝长度、射孔眼孔压等参数的影响。模拟结果显示： ①在两射孔异步压裂和两射孔同步压裂工况下，由于裂缝之间的干扰，最小水平主应力的大小和方向以及储层抗拉强度发生改变，进而改变了水力裂缝的扩展路径；②在3种工况下，单射孔压裂形成的水力裂缝宽度最小，储层岩石初始起裂压力最小；异步压裂形成的水力裂缝宽度最大，长度最大，储层岩石的初始起裂压力最大；两射孔同步压裂时形成的水力裂缝长度最短，宽度、初始起裂压力则位于前述2种工况之间；③射孔间距影响同步压裂和异步压裂时的初始起裂压力，缝宽最大值及裂缝长度等。模拟结果可为不同的场地条件及压裂需求下选取合适的压裂方法提供初步理论指导。

关键词： 水力压裂 ; 扩展有限元 ; 多射孔压裂 ; 应力干扰 ; 裂缝扩展

Abstract

Rock hydraulic fracturing involves a complex fluid-structure interaction process. The regularity of hydraulic fracture propagation and the coupling mechanism between fracturing fluid and rock mass are the current research hotspots and difficulties. The extended finite element method （XFEM） based on the ABAQUS platform has the advantages of high calculation accuracy and small calculation volume， and its soil module can simulate the process of fluid-structure interaction， analyzing the basic parameters such as the propagation path， width， and stress of hydraulic fractures. Based on the XFEM， this paper studied the influence of different conditions （single-perforation fracturing， two- perforation asynchronous fracturing， two-perforation synchronous fracturing） on hydraulic fracturing propagation path， fracture width， fracture length， perforation pressure and other parameters. The simulation results show that：（1） Under the conditions of two-perforation asynchronous fracturing and synchronous fracturing， the magnitude and direction of the minimum horizontal principal stress and the tensile strength of reservoir are changed due to the interference of hydraulic fractures. These changes in turn alter the propagation path of hydraulic fractures. （2） Among the mentioned three conditions， the width of hydraulic fracture formed by single-perforation fracturing is the smallest， and its initial fracture pressure of reservoir rock mass is the lowest. The hydraulic fracture formed by two-perforation asynchronous fracturing has the largest width， the longest length， and the highest initial fracture pressure of reservoir rock due to the interference of existing fracture. The values of width， and fracturing pressure of the hydraulic fracture under the synchronous fracturing are between the above two conditions and its fracture length is the shortest. （3） The perforation spacing has significant influence on the initiation pressure of reservoir， the maximal fracture width and length. The simulation results can provide theoretical guidance for selecting suitable fracturing methods under different conditions and fracturing requirements.

Keywords： Hydraulic fracturing ; Extended finite element ; Multi-perforation fracturing ; Stress interference ; Fracture propagation

PDF (8996KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

马许平, 曾庆利. 多射孔压裂对水力裂缝扩展规律的影响. 天然气地球科学[J], 2022, 33(2): 312-323 doi:10.11764/j.issn.1672-1926.2021.09.011

MA Xuping, ZENG Qingli. Influence of multi-perforation fracturing on the regularity of hydraulic fractures propagation. Natural Gas Geoscience[J], 2022, 33(2): 312-323 doi:10.11764/j.issn.1672-1926.2021.09.011

0 引言

水力压裂技术是指将含有稳定剂等各种添加剂的压裂液在高压条件下压入岩石储层，克服储层原始地应力和岩石的抗拉强度，使岩石产生水力裂缝，形成由人工裂缝和天然裂缝相互贯通的高渗透率渗流通道^［1］。自1947年美国堪萨斯州Hugoton气田实施首次商业水力压裂以来，水力压裂技术越来越广泛地应用于石油和天然气等油气资源的开采。水力压裂不仅提高了油气的采收率，也提高了可采油气的储量^［2］。水力压裂过程涉及到岩石骨架变形、裂缝萌生与扩展、裂缝相交、流体的流动、地层孔隙渗流等，是一个多场耦合的复杂力学过程^［3］。水力压裂后的裂缝形态极其复杂，它不仅与地应力和压裂工艺密切相关^［4］，也与射孔眼（同井不同位置，下同）密度、射孔眼与最大水平主应力夹角^［5］、射孔间距、压裂液黏度等因素有关^［6］。在水力压裂技术发展过程中，水力压裂的纯理论分析也在不断进步。ANDERSON等^［7］在Eaton公式的基础上考虑了应力集中问题，确定了储层岩石的起裂压力。SOLIMAN^［8］将Hoek-Broen的岩石失效准则应用于水平井压裂并确定了相应储层岩石起裂压力。LI等^［9］考虑了岩石的复杂特性和各向异性提出页岩储层孔隙压力和起裂压力的预测模型。陈勉^［10］基于储层岩石断裂力学推导出三维空间中水力裂缝激活和转向控制方程，将转向扩展的水力裂缝视为不连续的正应力条件下的连续延伸。张树翠等^［11］采用复变函数保角变换方法修正了传统附加应力场解析解，基于最大拉应力强度理论得出水力压裂主裂缝遇天然裂隙或层理后的开裂机理和扩展方向，基于莫尔强度理论分析讨论被裂纹穿过后的储层次裂缝形成机理。TENG等^［12］基于修正的Brinkman方程推导出了一个新的解析裂缝渗透率模型，该模型可以考虑裂缝壁黏性剪切对支撑裂缝有效渗透率的影响并可描述裂缝渗透率、支撑剂充填层渗透率、支撑剂充填层孔隙度和裂缝宽度之间的关系。室内实验研究也取得了一些有价值的成果，如万小乐等^［13］利用单轴实验研究层理对水力裂缝扩展的影响，张搏等^［14］利用真三轴实验研究排量对裂缝网络扩展形态的影响，但是室内实验也存在诸多局限性而不能有效反映地层真实的物理力学性质和复杂的非线性流动^［15］，同时成本高昂、效率低。随着计算机硬件的飞速发展和数值计算方法的不断创新，数值模拟已经成为研究水力压裂问题的重要方法，日益受到科学界和工程界的重视。

国内外许多学者尝试利用数值方法对水力压裂过程进行模拟。如HOSSAIN等^［15］利用数值模拟软件HYFRANC3D，研究了不同应力条件以及射孔眼角度对水力裂缝体积的影响。薛炳等^［16］基于三维有限元方法，采用渗流应力耦合模型，模拟了水力裂缝的扩展以及压裂液的渗流行为，分析了压力和隔层等因素对裂纹几何形态的影响。彪仿俊等^［17］利用ABAQUS软件，采用三维流固耦合有限元方法，模拟分析了水平地应力及水平地应力差、储层渗透率、岩石弹性模量、压裂液黏度、注入速率等因素对水平裂缝的形态、起裂压力、宽度等参数的影响。ZOU等^［18］引入孔隙压力节点约束法，基于三维有限元模型，建立了7个0厚度孔隙压力黏聚力单元层，模拟了吉林省珲春煤层气储层水力裂缝的起裂和扩展过程，并研究了在不同注入速率情况下的水力裂缝形态及孔隙压力的变化情况。XU 等^［19］基于所建立的全三维数学模型，提出了一种新的皮卡逐次逼近法求解方法，模拟了大庆油田在不同压裂液黏度时水力裂缝扩展规律。传统有限元方法在涉及到流固耦合、裂缝动态扩展等变形问题时，有限元网格可能会发生严重扭曲，导致计算精度下降或者计算无法收敛等问题，因此需要不断对网格进行重划分，造成计算量加大，同时计算也不容易收敛^［20］。基于上述原因，扩展有限元法（XFEM）应运而生。它在继承了有限元优点的基础上，考虑了裂纹的存在；它以单位分解法为基础，引入Heaviside函数和裂尖渐进位移场函数来反映裂纹面不连续特性，以及裂缝尖端应力集中和奇异性^［21］，因此XFEM在处理间断问题有着独特的优势。王小龙^［22］基于XFEM建立了二维非线性流固耦合水力压裂数值模型，对水平井多段压裂、正交各向异性岩石中裂缝扩展、水力裂缝与天然裂缝相交等问题进行了研究。龚迪光等^［23］借助ABAQUS模拟软件，通过编写扩展有限元程序，模拟了射孔眼角度、压裂液黏度、地应力差、压裂液排量对裂缝起裂压力、裂缝长度的影响。

在压裂施工过程中，缝间干扰是影响复杂裂缝网络形成进而影响气井产能的主要因素之一。国内外学者对此进行了研究和分析。BLANTON^［24］基于室内实验研究了天然裂缝对水力裂缝走向的影响，研究结果表明天然裂缝与水力裂缝之间的干扰角度和水平主应力差是影响水力裂缝走向的主要因素。尚校森等^［25］认为页岩发育的天然裂缝和层理等软弱结构是控制水力裂缝扩展路径，使水力裂缝停止、转向或产生新裂缝的主要因素。ZHANG等^［26］基于三轴水力压裂实验研究了不同方向具有封闭胶结的天然裂缝网络对水力裂缝走向、注入压力和声发射特征的影响，结果表明天然裂缝网络与最大水平主应力夹角是影响水力裂缝与天然裂缝连通的主要因素。张矿生等^［27］以平面二维水力裂缝的线弹性应力场为基础，采用应力叠加的方式计算了形成复杂裂缝网络最优缝间距。虽然前人对于水力压裂和裂缝之间的干扰问题有了大量研究，但对于多射孔压裂时水力裂缝之间的干扰问题研究较少。

本文在前人研究的基础上，基于ABAQUS软件，利用扩展有限元法（XFEM），研究了水力压裂过程中的缝间干扰问题，分析了在单射孔压裂、两射孔异步压裂、两射孔同步压裂3种工况下水力裂缝扩展规律，研究结果可以为水力压裂的设计和施工提供一定的理论指导和参考。

1 数学物理模型

1.1　耦合方程

水力压裂过程涉及到压裂液流体与岩石固体的动态耦合作用。在水力压裂过程中，当压裂液注入的压力不断增大，裂缝面的渗透压力和岩石储层的孔隙压力梯度也随之增大，进而导致储层有效地应力减小。储层有效地应力的变化又会影响储层岩体的渗透率、孔隙比、渗流速度等渗流参数变化。这些渗透参数的变化反过来会影响裂缝面渗透压力不断变化。因此，水力压裂过程是一个复杂的动态流固耦合过程。在利用计算机对水力压裂进行数值模拟时，主要通过耦合求解应力平衡方程和流体的连续性方程的方式来解决这一问题。

基于有效应力原理和虚功原理，ABAQUS软件以作用在岩体上的体力和面力所产生的虚功与岩体的虚功相等为依据，对水力压裂过程中考虑流体在岩石孔隙中流动的应力平衡方程进行了简化。其等效弱积分形式为^［28］：

\int_{V} (\bar{σ} - P_{W} I) ∶ δ ε d V = \int_{S} t ∙ δ v d S + \int_{V} f ∙ δ v d V

（1）

式中： $\bar{σ}$ 为储层基质有效应力，Pa； $δ ε$ 为储层基质虚变形率，s^-1； $δ v$ 为虚速度场，m/s； $P_{W}$ 为孔隙介质孔隙压力，Pa； $t$ 为单位面积表面外力，N/m²； $f$ 为单位体积的体力，N/m²； $I$ 为单位矩阵，无因次； $V$ 为积分区域，m³； $S$ 为积分区域的表面，m²。

在ABAQUS软件中，对划分的网格增加孔隙压力自由度，也就是在每个节点上增加孔隙水压力，就可模拟储层孔隙中流体的流动。根据流体质量守恒原理，即在一段时间内，流入储层介质的流体质量总和等于流出储层介质的流体和留在储层介质中的流体质量之和，便可推导出流体的连续性方程，其等效弱积分形式为^［28］：

\frac{d}{d t} (\int_{V} ρ_{w} n_{w} d V) + \int_{s} ρ_{w} n_{w} n ∙ v_{w} d S = 0

（2）

式中： $ρ_{w}$ 为流体密度，kg/m³； $n_{w}$ 为介质的孔隙度，无因次； $v_{w}$ 为流体相对于固相的平均速度，m/s； $n$ 表示表面S的外法向向量，无因次； $V$ 是积分区域，m³； $S$ 是积分区域的表面，m²； $t$ 为单位面积的表面外力，N/m²。

储层介质中孔隙流体的流动基本特征符合Darcy定理，根据Darcy定律，流动速度 $v_{w}$ 可以表示为^［28］：

v_{w} = - \frac{1}{n_{w} g ρ_{w}} k ∙ (\frac{\partial p_{w}}{\partial x} - p_{w} g)

（3）

式中： $k$ 为储层介质渗透率矩阵，m/s； $g$ 为重力加速度向量，9.8 m/s²； $P_{W}$ 为孔隙介质孔隙压力，Pa； $x$ 为空间向量，m。

ABAQUS软件使用Newton-Raphson迭代法对上述应力平衡方程（1）和流体的连续性方程（2）进行耦合求解，便可实现水力压裂过程的数值模拟。

1.2　裂纹扩展准则

ABAQUS软件有4种可以判断裂纹是否可以扩展的准则，即临界应力准则、临界裂纹扩展张开位移准则、裂纹长度时间曲线准则及虚拟裂纹闭合准则。临界应力准则适用于脆性材料，岩石材料在常温常压下大多属于脆性材料，并且因为水力压裂过程是一种拉伸破坏和剪切破坏，故裂纹的扩展是一种裂纹尖端脆性断裂的过程^［27］。因此本文在水力压裂数值模拟中使用临界应力准则来判断裂纹是否扩展。临界应力准则的定义如下^［29］：

\begin{array}{l} f = \sqrt[]{{(\frac{{\hat{σ}}_{n}}{σ^{f}})}^{2} + {(\frac{T_{1}}{{T_{1}}^{f}})}^{2} + {(\frac{T_{2}}{{T_{2}}^{f}})}^{2}}, \\ {\hat{σ}}_{n} = m a x (σ_{n}, 0) \end{array}

（4）

式中： $σ_{n}$ 是交界面处法向应力分量，Pa； $T_{1}$ 、 $T_{2}$ 为交界面处剪切应力分量，Pa； ${T_{1}}^{f}$ 、 ${T_{2}}^{f}$ 为剪切失效应力，Pa； $σ^{f}$ 为法向失效应力，Pa； $f$ 为计算得出的失效准则值，无因次。当计算得到的失效准则值 $f \geq$ 1.0时裂纹尖端节点开裂。

1.3　计算模型构建与实验方案

1.3.1　模型构建

基于ABAQUS软件建立100 m×100 m的二维计算模型，将该模型划分为0.5 m×0.5 m的正方形网格，射孔眼（A射孔眼与B射孔眼为同井不同位置，下同）位置及角度如图1所示。计算模型的边界条件为约束X方向的位移边界U₁=0，Y方向位移边界U₂=0，射孔眼与最大水平主应力夹角α为30°。模型具体参数参考龚迪广等^［23］、XU等^［19］相关文献（表1）。

图1

新窗口打开| 下载原图ZIP| 生成PPT

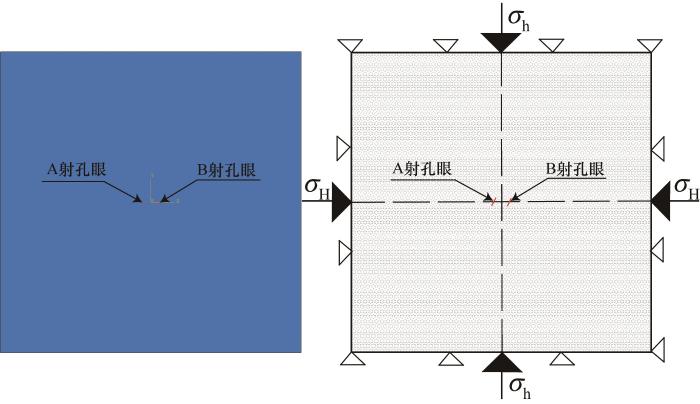
图1 计算模型示意

Fig.1 Sketch of the calculation model

表1 数值模拟基本参数^[19，23]

Table 1 Basic parameters of mumerical simulation^[19，23]

弹性模量/GPa	泊松比	岩石抗拉强度/MPa	排量/（m³/s）	渗透系数/（m/s）	滤失系数 $/ [m / (P a ∙ s)]$
12	0.25	3	0.01	1×10^-7	1×10^-11
注液时间/s	初始孔隙比	水平最大主应力/MPa	水平最小主应力/MPa	压裂液黏度 $/ (P a ∙ s)$
70	0.1	15	13	0.002

新窗口打开| 下载CSV

1.3.2　实验方案

本文主要研究水力裂缝之间干扰问题，包括水力裂缝的宽度、长度、扩展路径等。为保证实验条件一致性以及实验可对比性，两射孔眼距离设置为5 m^［30］，每一组的注液时间为70 s，孔隙水压力消散70 s。具体实验方案设计如下。

（1）工况一：仅对A射孔注液70 s，然后停止注液，孔隙水压力消散70 s（单孔压裂）。

（2）工况二：对A射孔与B射孔同步注液70 s，然后停止注液，孔隙水压力消散70 s（同步压裂）。

（3）工况三：先对A射孔注液70 s，停止注液，再对B射孔注液70 s，停止注液，然后孔隙水压力消散70 s（异步压裂）。

2 结果分析

2.1　3种工况下水力裂缝的扩展路径

为研究在有干扰情况下水力裂缝的扩展路径，对模拟结果进行后处理，得到单孔压裂、异步压裂、同步压裂3种工况下最小主应力在不同注液时刻的变化云图（图2—图4），图中不同颜色线段表示水平最小主应力大小不同，箭头则表示最小水平主应力方向。分析图2—图4发现，水力裂缝的扩展路径与裂缝两端最小主应力方向有密切关系。观察最小主应力方向，以及水力裂缝两端的尖端起裂方向，发现水力裂缝两端的尖端起裂方向与最小主应力方向垂直。

图2

新窗口打开| 下载原图ZIP| 生成PPT

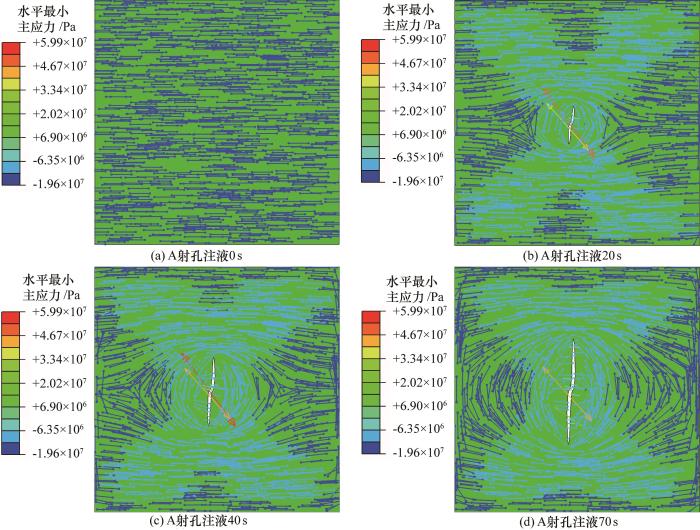
图2 单孔压裂时最小主应力等值线

Fig.2 Contour map of minimum principal stress during single-perforation fracturing

图3

新窗口打开| 下载原图ZIP| 生成PPT

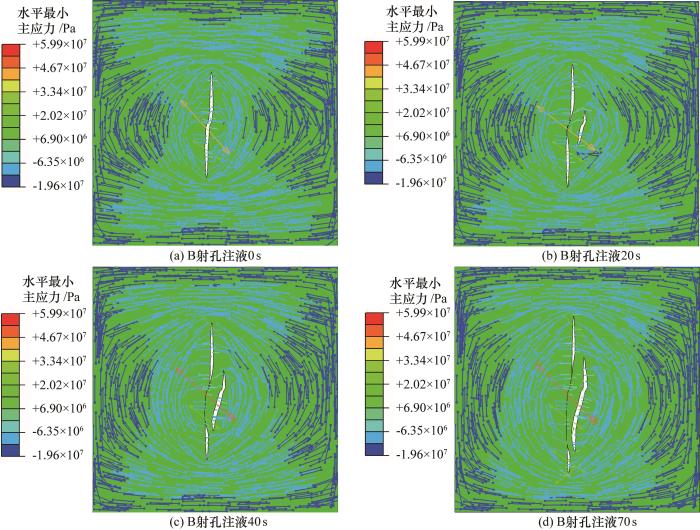
图3 异步压裂在B射孔注液时最小主应力等值线

Fig.3 Contour map of minimum principal stress during perforation B injection in asynchronous fracturing

图4

新窗口打开| 下载原图ZIP| 生成PPT

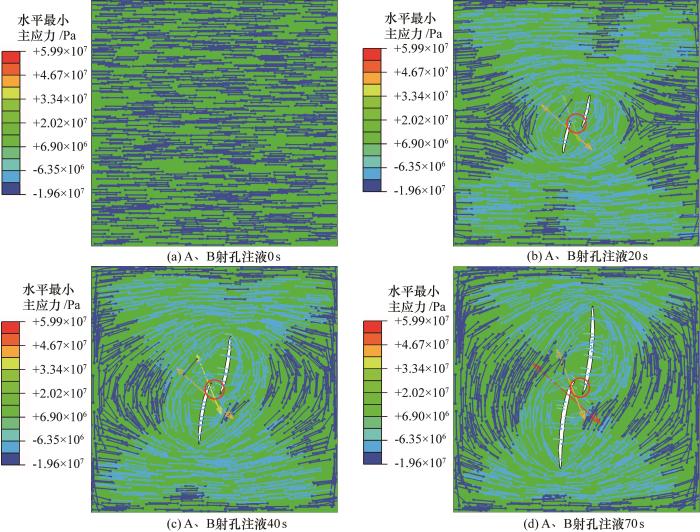
图4 同步压裂时最小主应力等值线（红圈为两注射孔分别引起的地应力变化重叠部分）

Fig.4 Contour map of minimum principal stress during synchronous fracturing(The red circle is the overlapping area of in-situ stress changes caused by two perforations)

分析单孔压裂形成的水力裂缝（图2），当射孔眼角度与最大水平主应力方向不平行时（本文射孔眼角度与初始最大水平主应力方向夹角为30°），初始注液时水力裂缝扩展路径与最大主应力方向不平行，但是当注液一段时间后，水力裂缝的扩展路径发生转向与最大水平主应力方向平行。这与前人研究结果一致^［31］，即水力裂缝沿平行于最大主应力方向、垂直于最小主应力方向扩展，当水力裂缝扩展路径与最大水平主应力方向不平行时，水力裂缝会向最大主应力方向转向。

图3为A射孔注液结束后，B射孔注液压裂时最小主应力在不同注液时刻的分布云图。单孔压裂时，初始最小主应力大小为13 MPa，方向平行于X轴的水平方向［图2（a）］，在A射孔注液结束后，B射孔开始注液前，B射孔附近最小主应力小于13 MPa，最小主应力方向与X轴夹角约为65°［图3（a）］。同时对比图2与图3在相同注液时刻水力裂缝两端的最小应力分布方向，可以看出单孔压裂时，水力裂缝两端的最小主应力方向始终平行于X轴；异步压裂时，在既有裂缝的影响下，水力裂缝两端最小主应力方向与X轴有一定的夹角。根据前文及前人的结论，水力裂缝扩展路径与最小主应力方向有密切关系，所以在既有裂缝影响下，水力裂缝扩展路径与无干扰单孔压裂形成的水力裂缝扩展路径不同。在B射孔压裂时，B射孔压裂对既有水力裂缝的挤压使既有水力裂缝中的压裂液向裂缝两端流动，进而导致既有裂缝向上下两端继续扩展，同时部分段发生闭合。

图4为两孔同步注液压裂最小水平主应力在不同注液时刻的应力云图。由图4可以看出，水力裂缝主要向上下两端扩展，在重叠区域内只有较小的扩展。这主要与两射孔眼分别引起的地应力变化范围重叠及两注液孔挤压有关。由前文所述，注液会引起一定范围内地应力大小及方向的变化，尤其是水力裂缝附件应力变化明显，因此当两射孔眼距离较近时，两射孔眼注液压裂分别引起的地应力变化范围会有部分区域重叠。对比分析各时刻重叠区域内及两条水力裂缝上下两端地应力大小，可发现重叠区域内的最小主应力大于水力裂缝上下两端的最小主应力。同时，在重叠区域内两孔注液产生挤压使两孔重叠区域之间储层抗拉强度增大。储层岩石的破裂压力与最小主应力及储层岩石抗拉强度成正相关的关系^［32］，重叠区域内储层岩石的破裂压力大于两条水力裂缝上下未破裂区域内储层的破裂压力，因此相对于重叠区域，水力裂缝更易向上下两端扩展，进而形成了如图4所示的水力裂缝。

2.2　3种工况下水力裂缝宽度、长度分布规律

比较3种工况下水力裂缝宽度云图（图5）可以发现，单孔压裂所形成的水力裂缝宽度最小，最大值为1.066 cm；受到已形成水力裂缝的影响，异步压裂所形成的水力裂缝宽度最大，最大值为1.409 cm；同步压裂形成的水力裂缝宽度居中，最大值为1.309 cm。比较3种工况下水力裂缝宽度分布位置发现，单孔压裂、异步压裂形成的水力裂缝宽度由注液点向水力裂缝两端逐渐减小，同步压裂形成的水力裂缝宽度由注液点向水力裂缝端部先增大后减小，这可能是因为2条水力裂缝之间的干扰造成最小水平主应力方向和大小改变，进而造成两射孔注液点形成较大的挤压力。此外当两孔异步压裂时，后注液压裂形成的水力裂缝会对已经停止注液的水力裂缝进行挤压，使得水力裂缝闭合。因此在实际施工过程中，需要对已形成的水力裂缝注入支撑剂防止水力裂缝闭合，并根据现场条件，选择合适的施工方法进行压裂。

图5

新窗口打开| 下载原图ZIP| 生成PPT

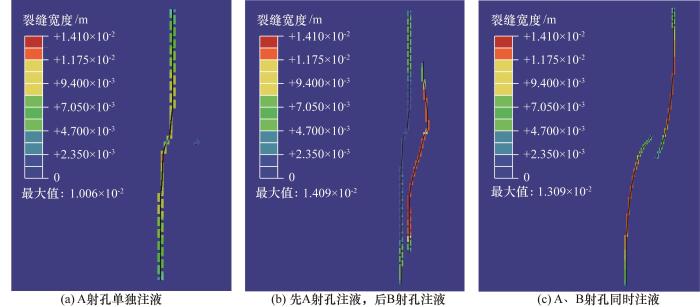
图5 水力裂缝宽度等值线

Fig.5 Contour map of hydraulic fracture width

分别提取单孔压裂射孔眼、同步压裂B射孔眼及异步压裂A射孔眼和B射孔眼附近监测单元，得到射孔眼裂缝宽度、孔隙压力随时间的变化曲线（图6，图7）。分析发现，3种工况下注液点裂缝宽度随注液时间增加呈现出不同变化趋势。单孔压裂注液点裂缝宽度随着注液时间增加先急剧增加，随后缓慢增加，并随注液时间的增加可能趋于一个稳定缝宽，当注液完成后，注液点裂缝宽度缓慢减小。在异步压裂中，当A射孔注液时，A射孔眼裂缝宽度变化曲线和单孔压裂注液变化时的曲线一致，B射孔眼裂缝宽度没有明显变化；A射孔注液完成后，B射孔开始注液前，A射孔注液点的裂缝宽度为0.014 m；A射孔注液完成后，B射孔注液时，A射孔受到B射孔挤压作用，A射孔注液完成后注液点缝宽变化曲线明显不同于单孔压裂注液完成后注液点缝宽变化曲线，注液点缝宽由0.014 m迅速减小至0.002 m（初始宽度为0.002 m），所用时间约为20 s；分析观察异步压裂B射孔注液点裂缝宽度变化曲线，在A射孔注液时，B射孔注液点裂缝宽度没有明显变化，当A射孔注液完成，B射孔注液时，B射孔注液点因既有水力裂缝产生的应力干扰，裂缝宽度最大值明显大于单孔压裂和同步压裂注液点裂缝宽度最大值；在B射孔注液过程中，当A射孔注液点裂缝闭合后，B射孔注液点缝宽有一段平稳期，随后继续增加，这可能是因为A射孔注液点裂缝迅速闭合后，B射孔受到的挤压力相对于A射孔裂缝闭合前受到的挤压力突然增大。两孔同步压裂时注液点裂缝宽度在注液初期同另外2种工况一样迅速增加，但是在22 s之后发生不同于另外2种工况的变化，即注液点缝宽达到了最大值，并且随着注液时间的增加，注液点缝宽开始以较小速率减小，这可能是因为同步压裂时A射孔和B射孔注液点互相挤压。这说明异步压裂和同步压裂都对注液点缝宽有较大影响。当注液结束后，孔隙水压力消散，水力裂缝支撑力减小，3种工况注液点的裂缝宽度均随着时间的增大而减小。

图6

新窗口打开| 下载原图ZIP| 生成PPT

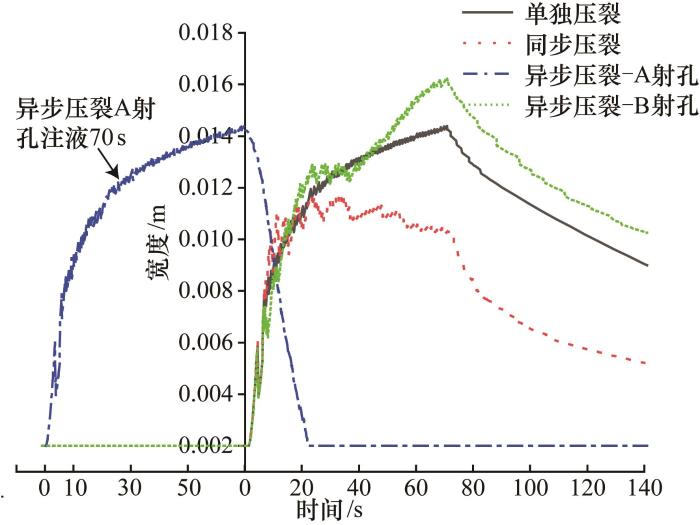
图6 射孔注液点裂缝宽度随压裂时间变化曲线

Fig.6 Hydraulic fracture width of perforation injection point versus the fracturing time

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 射孔注液点压力随时间变化曲线

Fig.7 Pore pressure at perforation injection point versus fracturing time

为对比3种工况下形成的单条水力裂缝长度，利用CAD软件分别提取单孔压裂，同步压裂B射孔，异步压裂B射孔形成的水力裂缝长度（表2）。从表2可知，异步压裂B射孔形成的水力裂缝长度最长，同步压裂B射孔形成的水力裂缝长度最短，单孔压裂形成的水力裂缝长度位于上述2种工况之间。从图7和图8可看出，在异步压裂时，当A射孔注液结束后，A射孔形成的水力裂缝对周围孔隙水压力已产生较大影响，例如B射孔注入点的孔隙水压力已增大至13 MPa，同时观察图8（b）可发现，A射孔形成的水力裂缝与B射孔形成的水力裂缝之间形成非常大的孔隙水压力，当B射孔进行注液压裂及注液结束后裂缝扩展时，因A射孔水力裂缝对岩体周围孔隙水压力影响，B射孔水力裂缝中的压裂液向周围岩体的渗流量非常小；单孔压裂和同步压裂在注液压裂及注液结束后裂缝扩展时由于初始孔隙水压力为静水压力，孔隙水压力非常小，且同步压裂2条水力裂缝扩展方向沿着反方向，相互影响的区域较小，所以单孔压裂和同步压裂水力裂缝中的压裂液向周围岩体的渗流量较大。在相同的注液时间内，每条水力裂缝的注液总体积是相等的，等于水力裂缝中的压裂液体积与向周围岩体渗流压裂液体积之和，所以异步压裂B射孔形成的水力裂缝内压裂液体积大于单孔压裂和同步压裂水力裂缝内的压裂液体积，异步压裂B射孔形成的水力裂缝宽度和长度都是最大的。单孔压裂和同步压裂水力裂缝内压裂液体积几乎一样，异步压裂B射孔形成的水力裂缝宽度大于单孔压裂，在压裂液体积一定的情况下，水力裂缝宽度越大，长度越短，所以单孔压裂水力裂缝长度大于同步压裂B射孔形成的水力裂缝长度。在异步压裂中，从形态上看虽然A射孔形成的水力裂缝长度最长，但是B射孔压裂挤压使A射孔水力裂缝部分闭合，A射孔有效宽度的水力裂缝长度反而最短。

表2 3种工况下的水力裂缝长度

Table 2 Hydraulic fracture length under three conditions

水力裂缝	单孔压裂	同步压裂	异步压裂A射孔	异步压裂B射孔
长度/m	45.56	42.58	20.63	48.52

新窗口打开| 下载CSV

图8

新窗口打开| 下载原图ZIP| 生成PPT

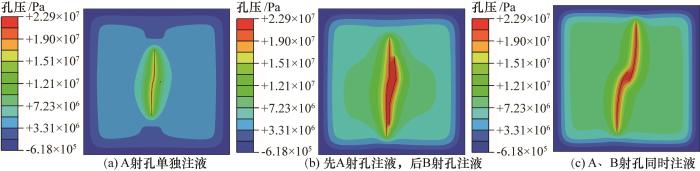
图8 孔隙水压力等值线

Fig.8 Pore water pressure contours

2.3　不同工况下孔压的分布规律

对模拟结果进行后处理，得到3种工况下孔压分布云图（图8）。分析发现，3种工况下不同梯度的孔压影响范围有差异即孔压影响程度不同。两孔同步压裂时，孔压影响程度最大，异步压裂其次，单孔压裂最小。孔压的差异分布主要与注液量和注液顺序有关。单孔压裂是3种工况里注液量最少的，所以影响程度最小。两孔同步压裂在70 s内注液量是单孔压裂的2倍，所以影响程度最大。异步压裂虽注液量和同步压裂相同，但压裂液是在140 s内注入的，孔隙水压力消散时间较长，所以影响程度大于单孔压裂，小于同步压裂。单孔压裂和同步压裂导致的孔压力大小在水力裂缝左右两边约相等，异步压裂B射孔注液压裂形成的水力裂缝和既有裂缝的挤压使得2条水力裂缝之间形成的孔压明显大于2条水力裂缝两边的孔压。这主要是因为2条水力裂缝之间孔压互相影响，2条水力裂缝之间孔压叠加。同时，无论是哪种工况，孔压变化明显的区域都位于水力裂缝附近，距离水力裂缝越远，孔压的变化越小。

分析射孔注液点孔压随时间变化曲线（图7）可知，无论是哪种工况，储层岩石在起裂时需要较大的注液压力，并且在岩石起裂后，孔压迅速减小。在单孔压裂时，当储层岩石起裂后，孔压迅速减小，并趋于一个稳定的值；当注液完成后，射孔注液点孔压开始缓慢减小。在异步压裂中，当A射孔注液时，A射孔注液点孔压和单孔压裂时射孔注液点孔压变化曲线一致，同时可发现B射孔注液点孔压受A射孔注液的影响也在缓慢增加但未达到储层岩石起裂所需孔压；A射孔注液完成后，B射孔注液开始前，B射孔注液点孔压达到13 MPa；A射孔注液完成后，B射孔注液时，受B射孔注液影响，A射孔注液完成后注液点孔压不同于单孔压裂注液完成后注液点孔压缓慢减小，而是以较小的速率增加。B射孔注液点岩石起裂压力因既有水力裂缝的影响明显大于单孔压裂和同步压裂，同时B射孔注液点孔压在储层岩石稳定破裂阶段的孔压大于单孔压裂时的孔压，小于同步压裂时的孔压。同步压裂射孔注液点岩石初始破裂时的孔压曲线同单孔压裂和异步压裂B射孔注液点孔压基本一致，但是当岩石起裂后，同步压裂射孔注液点孔压明显不同于单孔压裂和异步压裂B射孔注液点孔压，开始以较小的速率上升。

表3为不同工况下储层岩石的起裂压力，从表3可以看出，在3种工况下，异步压裂储层岩石的起裂压力最大，同步压裂起裂压力居中，单孔压裂起裂压力最小。这主要是因为在不同工况下，孔间干扰造成最小水平主应力大小和方向不同。因此在实际施工过程中，应该根据注液设备所能施加的最大注液压力以及其他条件选择不同施工方法。

表3 3种工况下储层岩石的初始起裂压力

Table 3 Initial fracture pressure of reservoir rock under three conditions

水力裂缝	单孔压裂	同步压裂	异步压裂B射孔
压力/MPa	65.1	67.6	74.5

新窗口打开| 下载CSV

2.4　射孔间距对水力裂缝起裂及扩展的影响

基于前文分析可知，在两射孔异步压裂和同步压裂时，水力裂缝之间的干扰对水力裂缝起裂和扩展有较大影响，因此在前文研究的基础上，选择射孔眼间距分别为5 m、8 m、15 m、20 m、30 m来研究射孔间距对水力裂缝起裂和扩展的影响。模拟结果见图9。

图9

新窗口打开| 下载原图ZIP| 生成PPT

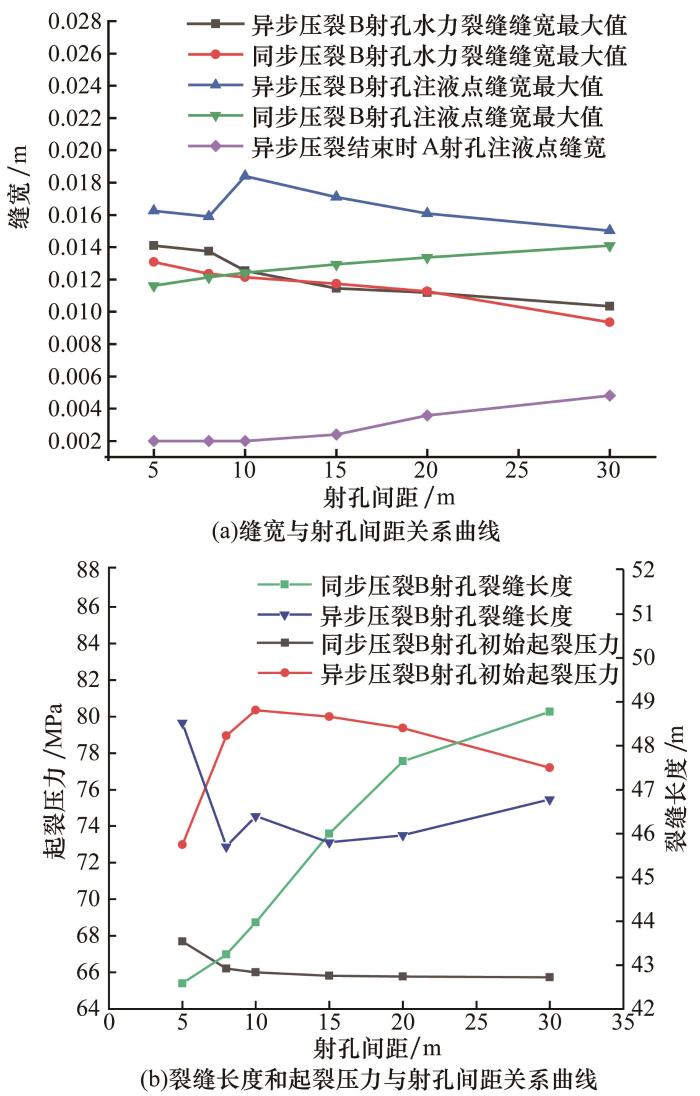
图9 射孔间距对裂缝扩展影响

Fig.9 Effect of perforation spacing on fracture propagation

研究结果显示，同步压裂和异步压裂B射孔水力裂缝宽度最大值随射孔间距增大逐渐减小。对于射孔注液点裂缝宽度最大值，同步压裂表现为随射孔间距的增大而增大，异步压裂B射孔整体上表现为随射孔间距增大而减小。在异步压裂过程中，从射孔间距为15 m起，A射孔注液点缝宽在B射孔注液压裂时没有发生闭合，且随射孔间距的增大而增大，这说明B射孔对A射孔的影响随射孔眼间距的增大逐渐减小。同步压裂和异步压裂B射孔起裂压力随射孔间距增大整体上逐渐减小且异步压裂起裂压力始终大于同步压裂起裂压力。同步压裂B射孔形成的水力裂缝长度随射孔间距的增大而增大，异步压裂B射孔形成的水力裂缝长度没有明显的规律，分析其有可能是因为在异步压裂过程中，A射孔注液压裂完成后对周围岩体孔隙水压力及地应力产生了较大改变。观察图9（b）可发现，在异步压裂过程中，当射孔间距为5 m和8 m时，B射孔注液点缝宽最大值及起裂压力表现异于两射孔距离较远时B射孔注液点缝宽最大值及起裂压力，分析其可能是因为距离A射孔形成的水力裂缝较近，且既有水力裂缝对裂缝附近孔隙水压力及地应力改变较大。这也进一步说明异步压裂既有水力裂缝对后压裂施工的水力裂缝起裂和扩展影响较大，裂缝之间的干扰更加复杂。

3 结论

本文利用ABAQUS软件建立了二维流固耦合水力压裂数值模型，并利用扩展有限法模拟了不同工况下水力裂缝之间的干扰问题，根据模拟结果得如下结论：

（1）同步压裂、异步压裂时、水力裂缝之间的干扰导致最小水平主应力以及储层岩石的抗拉强度变化，进而导致水力缝的扩展路径与单孔压裂不同。

（2）在3种工况下，在已有水力裂缝干扰下形成的水力裂缝宽度最大、水力裂缝长度最大；同步压裂形成的水力裂缝宽度位于单孔压裂和异步压裂之间、水力裂缝长度最小；单孔压裂形成的裂缝宽度最小、水力裂缝长度位于上述两者之间。在异步压裂时，当2条裂缝距离较近，后形成的水力裂缝会对已经形成的水力裂缝挤压使其闭合。

（3）在3种工况下，同步压裂注液点裂缝宽度最大值最小，异步压裂在已有裂缝干扰下注液点的裂缝宽度最大值最大，单孔压裂注液点裂缝宽度最大值位于上述两者之间。

（4）3种工况下最终导致的孔压影响程度不同，两孔同步注液压裂的影响程度最大，异步压裂其次，单孔注液压裂的影响程度最小。单孔压裂时储层岩石的初始起裂压力最小，异步压裂储层岩石初始起裂压力最大，同步压裂的储层岩石起裂压力位于两者之间。

（5）射孔间距对裂缝之间干扰影响较大，同步压裂水力裂缝宽度最大值和起裂压力随射孔间距增大而减小，注液点缝宽最大值和裂缝长度随射孔间距增大而增大。异步压裂B射孔水力裂缝宽度最大值，起裂压力及注液点缝宽最大值随射孔间距增大整体逐渐减小。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘曰武，高大鹏，李奇，等. 页岩气开采中的若干力学前沿问题［J］. 力学进展，2019，49（1）：1-236.