致密储层压裂缝扩展规律与可压裂性评价

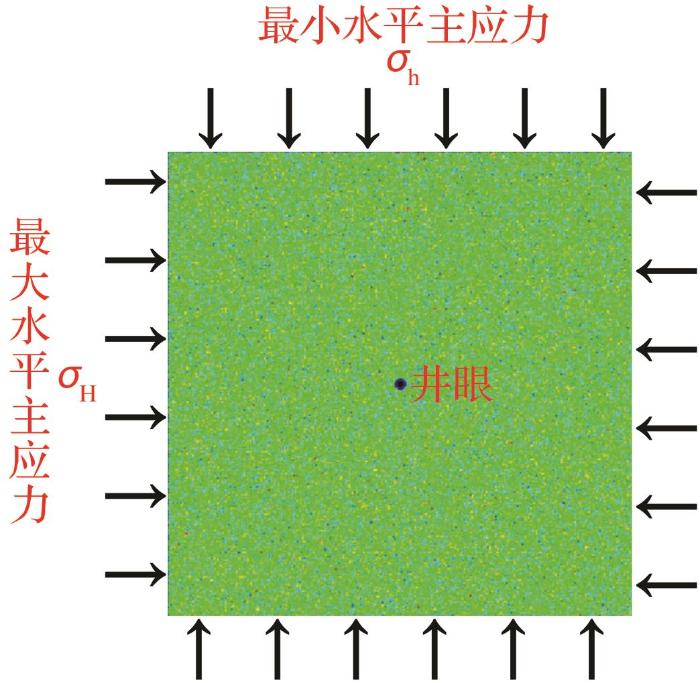
图1 二维井眼的水力压裂模型示意

Fig.1 Schematic diagram of hydraulic fracturing model for two dimensional borehole

表1 模拟的细观岩石力学参数

Table 1 The simulated mesoscopic rock mechanical parameters

参数	均质度	压拉比	抗压强度/MPa	弹性模量/GPa	泊松比	最小水平主应力/MPa	最大水平主应力/MPa
基质	3	25	470	28.7	0.31	90	100

新窗口打开| 下载CSV

利用RFPA-2Dflow软件平台构建了无结构面的非均质性的二维井眼水力压裂模型，其尺寸为1 500 mm×1 500 mm，模型的单元数目为300×300=90 000个。在模拟井眼中通过施加水头方式模拟压力，在模拟压裂过程中，水头压力初始值为55 MPa，压力加载模式为步增模式，单步增量为1.0 MPa，逐步增加井眼压力以模拟井筒压力的增加过程，直至地层压开形成裂缝并扩展延伸。为了分析和描述储层井周裂缝形成以及扩展延伸规律，主要模拟研究水平主应力差、单轴抗压强度、抗张强度、弹性模量及泊松比等因素对裂缝延伸的影响。

为定量分析各因素对压裂缝的影响程度，考虑到不同模拟方案的结果需要可对比性，选取在相同注入压力下的模拟结果图，利用IMAGEJ软件对模拟结果图［图2（a）］进行图像处理，处理结果如图2（b）所示，以此提取模型的裂缝形态。在此基础上，计算模拟结果的裂缝特征参数，并定义无因次压裂缝缝长和无因次压裂缝面积，前者描述压裂缝的延伸距离，后者描述压裂的改造区域，计算公式分别为：

l = \frac{L_{f}}{L}

(1)

A = \frac{h_{f} \times L_{f}}{L \times L}

(2)

式中：l为无因次压裂缝延伸距离；L_f为压裂缝长度，mm；L为模型长度，mm；A为无因次压裂缝面积，mm²；h_f为压裂缝区域宽度，mm。

图2

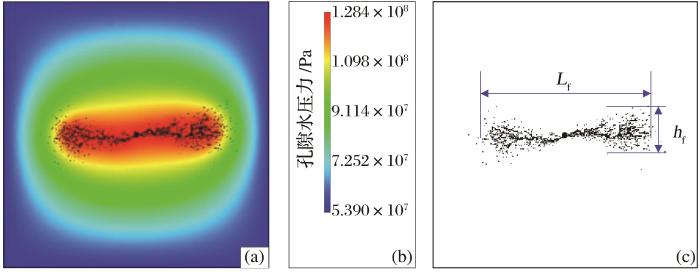
图2 压裂缝特征参数提取

（a）模拟结果；（b）色标；（c）二值化

Fig.2 Extraction of characteristic parameters of compressive fracture

需要注意的是为了研究不同因素对储层裂缝扩展规律的影响，选择在相同加载压力下的模拟结果进行对比，即选择在加载压力为122 MPa时的模拟结果作为基准图［图2（a）］，对应色标如图2（b）所示。

2 结果分析

2.1　水平主应力差的影响

通过数值模拟得到在不同水平主应力差条件下裂缝扩展阶段的孔隙水压力分布图（图3）。从图3中可看出，随着井内液柱压力增加，在井眼最大水平主应力方向左右两侧形成张应力区域，在拉张应力作用下井壁开始起裂，因岩石内部应力场分布不均匀，产生局部应力集中，裂缝主要沿最大水平主应力延伸且较为弯曲粗糙。同时，从图3中还可以看出围绕井眼附近生成的密集裂缝形成椭圆形裂缝区域，该区域随着水平主应力差的增大而增大，其长轴方向与最大水平主应力方向一致，裂缝发育密集，而纵向裂缝发育程度则较低。

图3

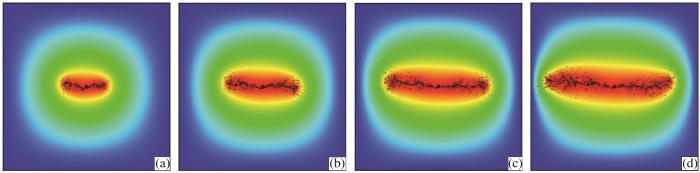
图3 水平主应力差对裂缝扩展规律的影响

（a）5 MPa；（b）10 MPa；（c）15 MPa；（d）20 MPa

Fig.3 Influence of horizontal principal stress difference on fracture propagation law

当模型中局部单元发生破坏时，出现少量声发射，但没有形成明显裂缝，随着液柱压力持续增大，声发射数持续增多，将逐渐形成主裂缝，但根据声发射数定量判断地层起裂压力的大小到目前为止还没有一个较为合理的判断条件。通常根据声发射数累计大小可定性判断地层起裂压力的相对大小，即在相同液柱压力条件下，声发射数累计越大，说明模型中破坏单元越多，反映出地层在较低压力下已经破裂，即起裂压力越低。基于数值模拟结果，统计了在不同水平主应力差条件下声发射数累计结果，如图4（a）所示；又统计了在不同水平主应力差条件下无因次压裂缝缝长的结果，如图4（b）所示。从图4中可以看出，随着水平主应力差增加，声发射数累计越大，即起裂压力越小，无因次裂缝缝长（延伸距离）呈增大的趋势。这主要是因为随着水平主应力差增大，模拟中的最小水平主应力越小，地层越易起裂，且在相同液柱压力下，裂缝沿着最大水平主应力的延伸距离较长。这与李树刚等^［10］研究结果一致。刘向君等^［11］、梁利喜等^［14-15］、赵海军等^［16］研究结果表明砾石结构、天然裂缝或层理结构的存在是井周形成复杂裂缝形态或裂缝网络的基础。赵海军等^［16］研究结果还表明无结构面的非均质地层的水力压裂缝主要沿最大水平主应力方向延伸。陈作等^［18］研究认为在高应力差条件下裂缝扩展形态相对简单，可通过实施缝内暂堵技术强制产生转向裂缝，以提高裂缝的复杂性和增大改造区域。

图4

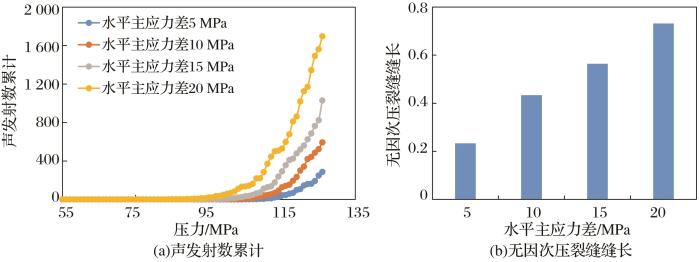
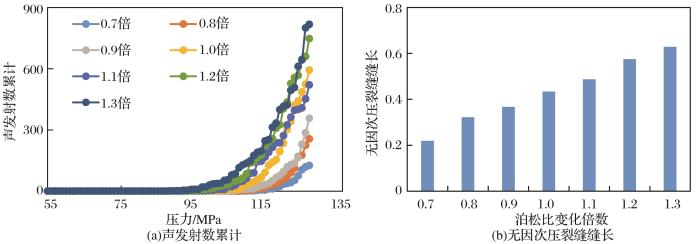
图4 不同水平主应力差条件下声发射数累计(a)和无因次压裂缝缝长(b)的变化规律

Fig.4 Variation rule of cumulative acoustic emission number(a) and dimensionless fracture length(b) under different horizontal principal stress differences

2.2　抗压强度的影响

通过数值模拟得到在不同抗压强度条件下裂缝扩展阶段的孔隙水压力分布图（图5）。

图5

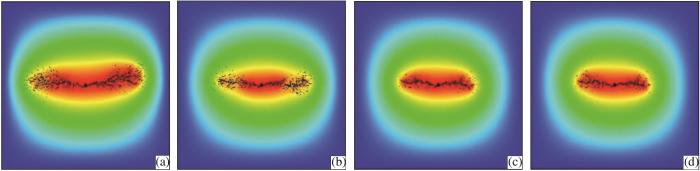
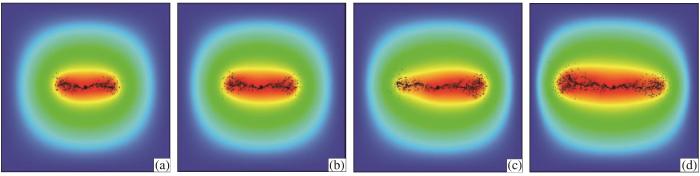
图5 抗压强度对裂缝扩展规律的影响

（a）0.8倍；（b）0.9倍；（c）1.1倍；（d）1.2倍

Fig.5 Influence of compressive strength on fracture propagation law

从图5中可以看出，椭圆形裂缝区域随着抗压强度的增大而减小，其长轴方向与最大水平主应力方向一致，裂缝发育密集，而纵向方面裂缝发育程度则较低。

基于数值模拟结果，统计了在不同抗压强度条件下声发射数累计结果，如图6（a）所示；又统计了在不同抗压强度条件下无因次压裂缝缝长的结果，如图6（b）所示。从图6中可以看出，随着抗压强度增加，声发射数累计减小，即起裂压力增大，无因次压裂缝延伸距离呈减小的趋势。这主要是因为随着抗压强度增大，地层起裂需要更高液柱压力才能使地层发生破坏，造成地层形成压裂缝需要更高液柱压力，且在相同液柱压力下，裂缝沿着最大水平主应力的延伸距离减小。

图6

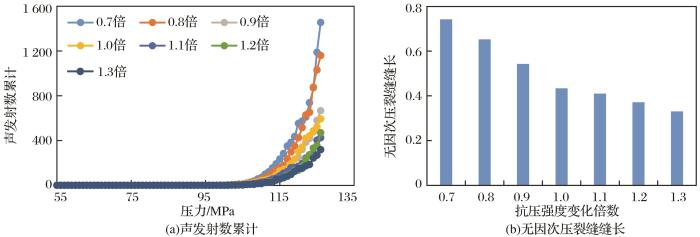
图6 不同抗压强度条件下声发射数累计(a)和无因次压裂缝缝长(b)的变化规律

Fig.6 Variation rule of cumulative acoustic emission number(a) and dimensionless fracture length(b) under different compressive strengths

2.3　抗张强度的影响

通过数值模拟得到在不同抗张强度条件下裂缝扩展阶段的孔隙水压力分布图（图7）。从图7中可看出，椭圆形裂缝区域随着抗张强度的增大而减小，其长轴方向与最大水平主应力方向一致，裂缝发育密集，而纵向方面裂缝发育程度则较低。

图7

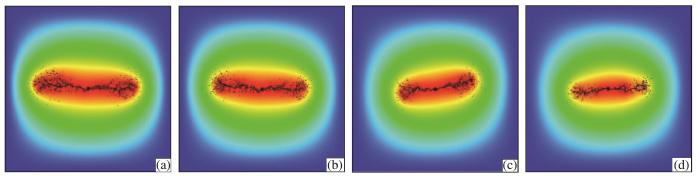
图7 抗张强度对裂缝扩展规律的影响

（a）0.8倍；（b）0.9倍；（c）1.1倍；（d）1.2倍

Fig.7 Influence of tensile strength on fracture propagation law

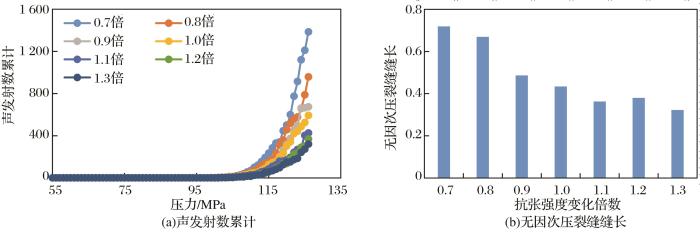
基于数值模拟结果，统计了在不同抗张强度条件下声发射数累计结果，如图8（a）所示；又统计了在不同抗张强度条件下无因次压裂缝缝长的结果，如图8（b）所示。从图8中可以看出，随着抗张强度增加，声发射数累计减小，即起裂压力增大，无因次压裂缝延伸距离呈减小的趋势。这主要是因为随着抗张强度增大，地层发生张性破裂需要更高液柱压力才能使地层发生起裂，造成地层形成压裂缝需要更高的液柱压力，且在相同液柱压力下，裂缝沿着最大水平主应力的延伸距离减小。

图8

图8 不同抗张强度条件下声发射数累计(a)和无因次压裂缝缝长(b)的变化规律

Fig.8 Variation rule of cumulative acoustic emission number(a) and dimensionless fracture length(b) under different tensile strengths

2.4　弹性模量的影响

通过数值模拟得到在不同弹性模量条件下裂缝扩展阶段的孔隙水压力分布图（图9）。从图9中可看出，椭圆形裂缝区域随着弹性模量的增大而减小，其长轴方向与最大水平主应力方向一致，裂缝发育密集，而纵向裂缝发育程度则较低。

图9

图9 不同弹性模量条件下渗流水力压力云图

（a）0.6倍；（b）0.8倍；（c）1.2倍；（d）1.4倍

Fig.9 Cloud image of seepage hydraulic pressure nephogram under different elastic modulus

基于数值模拟结果，统计了在不同弹性模量条件下声发射数累计结果，如图10（a）所示；也统计了在不同弹性模量条件下无因次压裂缝缝长的结果，如图10（b）所示。从图10中可看出，随着弹性模量增加，声发射数累计减小，即起裂压力增大，无因次裂缝延伸距离呈减小的趋势。这主要是因为随着弹性模量增大，地层的刚度增强，即地层强度增大，地层需要更高的液柱压力才能使地层发生破坏，造成地层形成压裂缝需要更高的液柱压力，且在相同液柱压力下，裂缝沿着最大水平主应力的延伸距离减小。

图10

图10 不同弹性模量条件下声发射数累计(a)和无因次压裂缝缝长(b)的变化规律

Fig.10 Variation rule of cumulative acoustic emission number(a) and dimensionless fracture length(b) under different elastic modulus

2.5　泊松比的影响

通过数值模拟得到在不同泊松比条件下裂缝扩展阶段的孔隙水压力分布图（图11）。从图11中可以看出，椭圆形裂缝区域随着泊松比的增大而增大，其长轴方向与最大水平主应力方向一致，裂缝发育密集，而纵向方面裂缝发育程度则较低。基于数值模拟结果，统计了在不同泊松比条件下声发射数累计结果，如图12（a）所示；也统计了在不同泊松比条件下无因次压裂缝缝长的结果，如图12（b）所示。从图12中可看出，随着泊松比增加，声发射数累计增大，即起裂压力降低，无因次裂缝延伸距离呈增大的趋势。这主要是因为随着泊松比增大，地层的延展性好，且在相同液柱压力下，裂缝沿着最大水平主应力的延伸距离增大。

图11

图11 泊松比对裂缝扩展规律的影响

（a）0.8倍；（b）0.9倍；（c）1.1倍；（a）1.2倍

Fig.11 Influence of Poisson's ratio on fracture propagation

图12

图12 不同泊松比条件下声发射数累计(a)和无因次压裂缝缝长(b)的变化规律

Fig.12 Variation rule of accumulated acoustic emission number(a) and dimensionless fracture length(b) change under different Poisson's ratios

3 可压裂性评价

基于数值模拟结果，虽然从定量化角度分析了水平主应力差、抗压强度、抗张强度、弹性模量和泊松比等因素对压裂缝延伸规律的影响，也只是从定性角度分析了各因素对压裂缝的影响，但是各因素的影响程度仍需进一步定量化研究。李小刚等^［19］、龙章亮等^［20］利用灰色关联方法定量研究了影响储层压裂效果的主控因素，这说明灰色关联法是一种分析各因素影响程度的有效方法。灰色关联法可求解未知的非线性问题中各影响因素的灰色关联度，反映各影响因素对目标函数的重要性，可避免人为经验确定各因素指标权重的主观性。因此，基于数值模拟结果，利用灰色关联法分析水平主应力差、抗压强度、抗张强度、弹性模量和泊松比等因素对压裂效果的影响程度。在数值模拟中压裂效果用无因次压裂缝缝长为评价指标，并用无因次压裂缝面积作为验证指标。

对各因素和无因次压裂缝缝长采用极值变换法［式（3）］进行归一化处理。以归一化处理后无因次压裂缝缝长为参考序列，以归一化处理后各因素为比较序列，对各因素和无因次压裂缝缝长进行关联度计算［式（4）］，其是通过位移差来评价各因素与无因次压裂缝缝长间的相似程度，位移差越小，关联度越接近1，则两者的形态越接近，反之，两者的相似程度越低。

\begin{array}{l} Y_{i} (k) = \frac{X_{i} (k) - m i n X_{i} (k)}{m a x X_{i} (k) - m i n X_{i} (k)} \\ (i = 1,2, \dots, m; k = 1,2, \dots, n) \end{array}

(3)

ξ_{i} (k) = \frac{\underset{i}{m i n} \underset{k}{m i n} Δ_{i} (k) + ρ \underset{i}{m a x} \underset{k}{m a x} Δ_{i} (k)}{Δ_{i} (k) + ρ \underset{i}{m a x} \underset{k}{m a x} Δ_{i} (k)}

(4)

式中：ξ_i（k）为第i个影响因素的第k个参考点的关联系数； $Δ_{i}$ （k）为归一化后的第i个影响因素值［X_i（k）］与参考数列值［X₀（k）］差值的绝对值， $Δ_{i} (k) = |X_{0} (k) - X_{i} (k)|$ ；ρ为分辨系数，一般情况取0.5。

关联系数的平均值能定量反映各因素的关联程度。因此，对各因素的关联系数进行均值化处理，计算公式为：

γ_{i} = \frac{1}{n} \sum_{k = 1}^{n} ξ_{i} (k)

(5)

式中： $γ_{i}$ 为第i个比较数列的关联度；n为该数列中参考点总数。

基于数值模拟结果，各因素的关联度大小计算结果如表2所示，根据关联度大小可确定各因素对压裂效果的影响程度。从表2中可看出，各因素的关联度大小存在较明显差异，根据其值的相对大小可明确各因素的影响程度顺序，则各因素对压裂效果的影响程度从大到小排序依次为水平应力差>弹性模量>抗张强度>单轴抗压强度>泊松比。

表2 各因素与无因次压裂缝缝长的关联度及排序

Table 2 Correlation degree and sequence of various factors with dimensionless fracture length

因素	水平主应力差	单轴抗压强度	抗张强度	弹性模量	泊松比
关联度	0.632	0.570	0.556	0.622	0.553
排序	1	4	3	2	5

新窗口打开| 下载CSV

在各因素对压裂效果影响程度研究的基础上，综合考虑水平应力差、弹性模量、抗张强度及单轴抗压强度的影响，利用层次分析法确定各因素的权重系数，从而构建评价储层的可压裂性。根据层次分析法原理，对影响压裂效果的因素进行正向或负向归一化处理^［21-22］，使所有因素都变成正向参数，即经归一化处理后的因素越大，无因次压裂缝延伸距离越大。在此基础上，对考虑因素进行两两对比来衡量各因素的权重，引用数字1~9和对应的倒数来标度，确定各因素的权重^［21-22］，构造出判断矩阵，构建的储层可压裂性指数判断矩阵如表3所示。在此基础上，利用层次分析理论中的特征向量法计算各因素的权重向量，即各因素的权重系数，则计算得到水平应力差、弹性模量、抗张强度、单轴抗压强度等因素的权重系数依次为0.423 6、0.227、0.227、0.122 3。

表3 储层可压裂性指数判断矩阵

Table 3 Fracability index judgment matrix of reservoir

	水平应力差	弹性模量	抗张强度	单轴抗压强度
水平应力差	1	2	2	3
弹性模量	1/2	1	1	2
抗张强度	1/2	1	1	2
单轴抗压强度	1/3	1/2	1/2	1

新窗口打开| 下载CSV

基于层次分析法，构建了综合考虑水平应力差、弹性模量、抗张强度及单轴抗压强度等影响储层可压裂性的指数计算模型：

F I = 0.423 6 Δ σ_{g} + 0.227 E_{g} + 0.277 σ_{t g} + 0.122 3 σ_{c g}

(6)

式中：FI为储层可压裂性指数；∆σ_g为归一化水平应力差；E_g为归一化弹性模量；σ_tg为归一化抗张强度；σ_cg为归一化单轴抗压强度。

根据所构建的储层可压裂性指数计算模型，基于数值模拟结果，计算可压裂性指数与无因次压裂缝缝长间的关系，如图13（a）所示。从图13（a）中可以发现可压裂性指数与无因次压裂缝缝长存在较好的正相关性。同时，统计分析了可压裂性指数与无因次压裂缝面积间的关系，如图13（b）所示。从图13（b）中也可发现可压裂性指数与无因次压裂缝面积存在较好的正相关性，即可压裂性指数越大，无因次裂缝面积越大，压裂改造区域越大。这说明了所构建的权重系数具有一定的可靠性，或综合考虑水平应力差、弹性模量、抗张强度及单轴抗压强度等影响储层的可压裂性指数具有一定可靠性。

图13

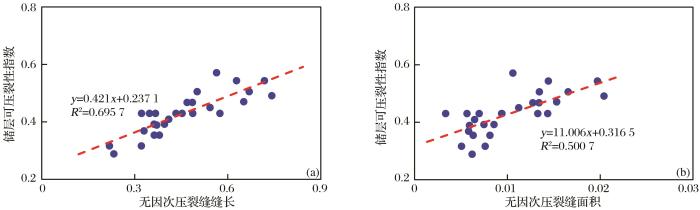
图13 可压裂性指数与无因次压裂缝缝长(a)和无因次压裂缝面积(b)的关系

Fig.13 Relationship between fracture ability index and dimensionless fracture length (a) and dimensionless fracture length area (b)

在此基础上，通过已压裂井的试油资料进一步分析所构建的可压裂性指数的适用性。准噶尔盆地玛湖凹陷玛页1井是在钻井过程钻遇风城组多套油层的直井。完钻后，对该层进行分段多级压裂，总共进行了25个小层射孔，分13级进行水力压裂，其岩石力学参数和压裂段如图14所示。在试产阶段进行产液剖面测试，获取每层对总产油量的贡献，从而获取每层的日采油量，再结合储层测井解释数据，就能获得每层的采油强度。根据射孔段从测井曲线图（图14）中提取出每段的水平主应力差、弹性模量、抗张强度及抗压强度等参数信息，根据构建的可压裂性指数计算模型，计算得到储层可压裂性指数，统计储层可压裂性指数与采油强度之间的关系，如图15所示。从图15中可以看出储层可压裂性指数与采油强度呈较好的正相关性，即储层可压裂性指数值越大，储层压裂效果越好，采油强度值越大。这说明所构建的可压裂性指数适用于风城组致密储层，可为风城组致密储层的直井压裂选层、选段等压裂设计提供参考。

图14

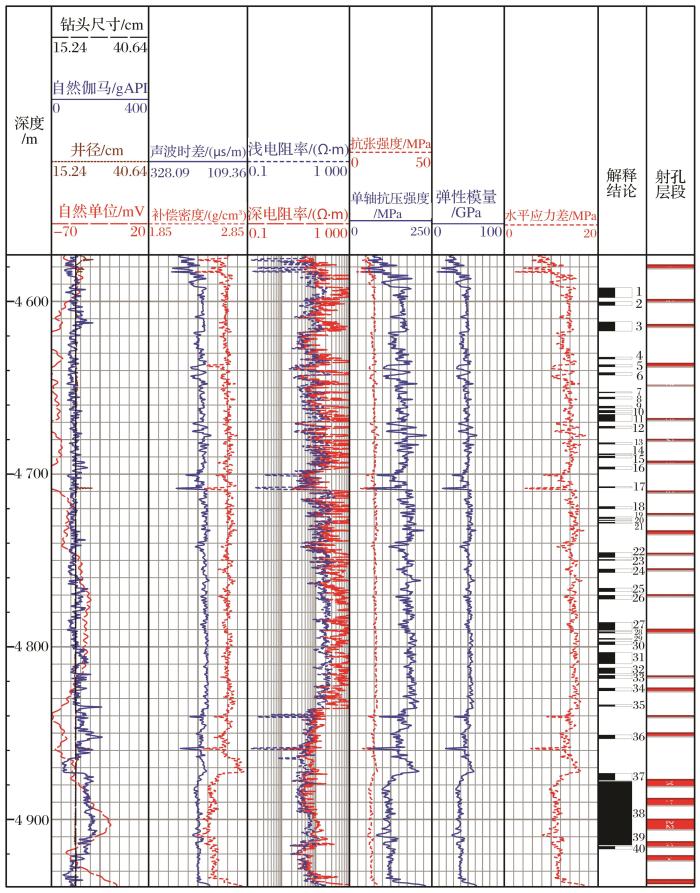
图14 玛页1井风城组地层岩石力学参数剖面特征

Fig.14 Rock mechanical parameters profile of Fengcheng Formation in Well MY 1

图15

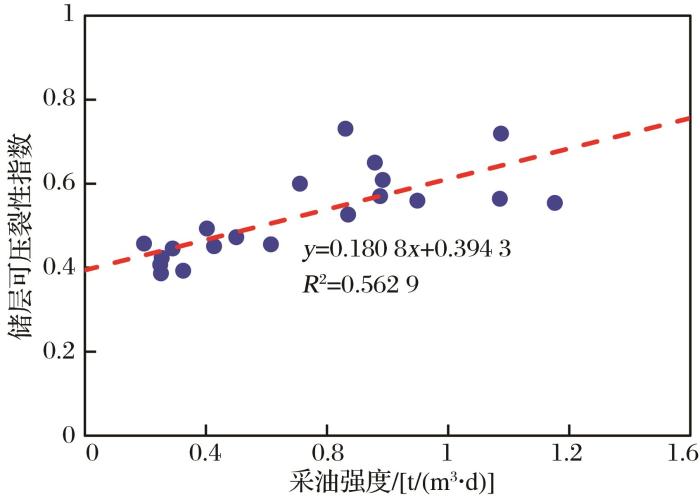
图15 可压裂性指数和采油强度间的关系

Fig. 15 Relationship between the fracability index and the recovery strength

4 结论

（1）水平主应力差越大，压裂缝延伸的方向性越明显，地层起裂压力越低，裂缝延伸距离越大。

（2）随着抗压强度、抗张强度和弹性模量的增大，地层起裂压力越高，裂缝延伸距离越小，而随着泊松比的增大，地层起裂压力越低，裂缝延伸距离越大。

（3）运用灰色关联法和层次分析法确定了综合考虑水平应力差、弹性模量、抗张强度、单轴抗压强度等因素的权重系数，进而构建了储层可压裂性指数计算模型，其与采油强度呈良好的正相关性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

廖晓蓉，郭焦锋，李维明.加大力度开发致密油和页岩油增强国家能源安全保障［J］.中国矿业，2013，22（7）：8-9.

LIAO X R， GUO J F， LI W M. Make greater efforts to develop tight oil and shale oil enhance the security of national energy［J］. China Mining Magazine，2013，22（7）：8-9.

[2]

李国欣，朱如凯.中国石油非常规油气发展现状、挑战与关注问题［J］.中国石油勘探，2020，25（2）：1-13.

LI G X， ZHU R K. Progress， challenges and key issues of unconventional oil and gas development of CNPC［J］. China Petroleum Exploration，2020，25（2）：1-13.

[3]

焦方正.陆相低压页岩油体积开发理论技术及实践［J］.天然气地球科学，2021，32（6）：836-844.

JIAO F Z. Theoretical technologies and practices concerning “volume development” of low pressure continental shale oil： Case study of shale oil in Chang 7 Member， Ordos Basin， China［J］. Natural Gas Geoscience，2021，32（6）： 836-844.

[4]

杨智，唐振兴，陈旋，等.“进源找油”：致密油主要类型及地质工程一体化进展［J］.中国石油勘探，2020，25（2）：73-83.

YANG Z， TANG Z X， CHEN X， et al. “Exploring oil inside source kitchen”： Main types of tight oil and progress of geology-engineering integration［J］. China Petroleum Exploration，2020，25（2）：73-83.

[5]

慕立俊，赵振峰，李宪文，等.鄂尔多斯盆地页岩油水平井细切割体积压裂技术［J］.石油与天然气地质，2019，40（3）：626-635.

MU L J， ZHAO Z F， LI X W， et al. Fracturing technology of stimulated reservoir volume with subdivision cutting for shale oil horizontal wells in Ordos Basin［J］. Oil & Gas Geology，2019，40（3）：626-635.

[6]

周立宏，赵贤正，柴公权，等.陆相页岩油效益勘探开发关键技术与工程实践——以渤海湾盆地沧东凹陷古近系孔二段为例［J］.石油勘探与开发，2020，47（5）：225-232.

ZHOU L H， ZHAO X Z， CHAI G Q， et al. Key exploration & development technologies and engineering practice of continental shale oil： A case study of Member 2 of Paleogene Kongdian Formation in Cangdong Sag， Bohai Bay Basin， East China［J］. Petroleum Exploration and Development，2020，47（5）：225-232.

[7]

门晓溪，唐春安，李宏，等.单裂隙岩体水力裂缝扩展机理的数值模拟［J］.应用力学学报，2014，31（2）：261-264.

MEN X X， TANG C A， LI H， et al. Numerical simulation on propagation mechanism of hydraulic fracture on fractured rockmass［J］. Chinese Journal of Applied Mechanics，2014，31（2）：261-264.

[8]

宋晨鹏，卢义玉，夏彬伟，等.天然裂缝对煤层水力压裂裂缝扩展的影响［J］.东北大学学报：自然科学版，2014，35（5）：756-760.

SONG C P， LU Y Y， XIA B W， et al. Effects of natural fractures on hydraulic fractures propagation of coal seams［J］.Journal of Northeastern University： Natural Science，2014，35（5）：756-760.

[9]

郭鹏，姚磊华，任德生.体积压裂裂缝分布扩展规律及压裂效果分析——以鄂尔多斯盆地苏53区块为例［J］.科学技术与工程，2015，15（24）：46-51.

GUO P， YAO L H， REN D S. Fracture distribution and propagation laws and effect analysis of volume fracturing in the Su 53 Block， Ordos Basin［J］. Science Technology and Engineering，2015，15（24）：46-51.

[10]

李树刚，马瑞峰，许满贵，等.地应力差对煤层水力压裂的影响［J］.煤矿安全，2015，46（3）：140-144.

LI S G， MA R F， XU M G， et al. Influence of ground stress deviation on coal seam hydraulic fracturing［J］. Safety in Coal Mines，2015，46（3）：140-144.

[11]

刘向君，熊健，梁利喜，等.玛湖凹陷百口泉组砂砾岩储集层岩石力学特征与裂缝扩展机理［J］.新疆石油地质，2018，39（1）：83-91.

LIU X J， XIONG J， LIANG L X， et al. Rock mechanical characteristics and fracture propagation mechanism of sandy conglomerate reservoirs in Baikouquan Formation of Mahu Sag［J］. Xinjiang Petroleum Geology，2018，39（1）：83-91.

[12]

张子麟，陈勇，张全胜，等.致密砂砾岩压裂裂缝遇砾扩展模式的数值模拟研究［J］.油气地质与采收率，2019，26（4）：132-138.

ZHANG Z L， CHEN Y， ZHANG Q S， et al. Numerical simulation on propagation mode of hydraulic fracture approaching gravels in tight glutenite［J］.Petroleum Geology and Recovery Efficiency，2019，26（4）：132-138.

[13]

何其胜，王贵君.砂砾岩水压致裂机理及数值仿真研究［J］.三峡大学学报：自然科学版，2020，42（6）：45-49.

HE Q S， WANG G J. Mechanism and numerical simulation of hydraulic cracking of sand and gravel［J］.Journal of China Three Gorges University：Natural Sciences，2020，42（6）：45-49.

[14]

梁利喜，黄静，刘向君，等.天然裂缝对页岩储层井周诱导缝形成扩展的影响［J］.地质科技情报，2014，33（5）：160-165.

LIANG L X， HUANG J， LIU X J， et al. Effect of natural fracture on formation and propagation of induced fracture around borehole in shale reservoir［J］. Geological Science and Technology Information，2014，33（5）：160-165.

[15]

梁利喜，黄静，刘向君，等.天然裂缝对页岩储层网状诱导缝的控制作用［J］.成都理工大学学报：自然科学版，2016，43（6）：696-702.

LIANG L X， HUANG J， LIU X J， et al. Formation and controlling effect of natural fractures on network induced fractures in shale reservoir［J］. Journal of Chengdu University of Technology： Science & Technology Edition，2016，43（6）：696-702.

[16]

赵海军，马凤山，刘港，等.不同尺度岩体结构面对页岩气储层水力压裂裂缝扩展的影响［J］.工程地质学报，2016，24（5）：992-1007.

ZHAO H J， MA F S， LIU G， et al. Influence of different scales of structural planes on propagation mechanism of hydraulic fracturing［J］. Journal of Engineering Geology，2016，24（5）：992-1007.

[17]

WANG Y， LIU X， LIANG L， et al. The influence of bedding planes and permeability coefficient on fracture propagation of horizontal wells in stratification shale reservoirs［J］. Geofluids，2020，1642142.

[18]

陈作，李双明，陈赞，等.深层页岩气水力裂缝起裂与扩展试验及压裂优化设计［J］.石油钻探技术，2020，48（3）：70-76.

CHEN Z， LI S M， CHEN Z， et al. Hydraulic fracture initiation and extending tests in deep shale gas formations and fracturing design optimization［J］. Petroleum Drilling Techniques，2020，48（3）：70-76.

[19]

李小刚，郑阳，瞿建华，等.基于灰色关联方法的砂砾岩油藏压后产量影响因素分析［J］.油气藏评价与开发，2016，6（4）：28-33.

LI X G， ZHENG Y， QU J H， et al. Influential factors of postfracture production of glutenite reservoir based on gray correlation method［J］. Reservoir Evaluation and Development，2016，6（4）：28-33.

[20]

龙章亮，温真桃，李辉，等.一种基于灰色关联分析的页岩储层可压性评价方法［J］.油气藏评价与开发，2020，10（1）：37-42.

LONG Z L， WEN Z T， LI H， et al. An evaluation method of shale reservoir crushability based on grey correlation analysis［J］. Reservoir Evaluation and Development，2020，10（1）：37-42.

[21]

赖富强，罗涵，覃栋优，等.基于层次分析法的页岩气储层可压裂性评价研究［J］.特种油气藏，2018，25（3）：154-159.

LAI F Q， LUO H， QIN D Y， et al. Crushability evaluation of shale gas reservoir based on analytic hierarchy process［J］. Special Oil & Gas Reservoirs，2018，25（3）：154-159.

[22]

崔春兰，董振国，吴德山.湖南保靖区块龙马溪组岩石力学特征及可压性评价［J］.天然气地球科学，2019，30（5）：626-634.

CUI C L， DONG Z G， WU D S. Rock mechanics study and fracability evaluation for Longmaxi Formation of Baojing Block in Hunan Province［J］. Natural Gas Geoscience，2019，30（5）：626-634.