天然气地球科学 >

2025 , Vol. 36 >Issue 6: 1000 - 1011

DOI: https://doi.org/10.11764/j.issn.1672-1926.2025.03.008

天然气开发

基于低速非达西渗流的致密气井储量动用评价模型

  • 王泽川 , 1, 2 ,
  • 田冷 , 1, 2 ,
  • 李进步 3 ,
  • 李鹏 3 ,
  • 柴晓龙 1, 2 ,
  • 邓小娇 4 ,
  • 蒋丽丽 1, 2
展开
  • 1. 中国石油大学（北京）石油工程学院，北京 102249
  • 2. 中国石油大学（北京）天然气地质与工程研究中心，北京 102249
  • 3. 中国石油长庆油田分公司勘探开发研究院，陕西 西安 710018
  • 4. 中国石油集团油气和新能源分公司，北京 100007
田冷（1977-），男，黑龙江哈尔滨人，博士，教授，主要从事非常油气藏渗流理论与应用研究. E-mail：.

王泽川（1996-），男，宁夏银川人，博士研究生，主要从事致密砂岩气藏渗流机理及提高采收率研究.E-mail：.

收稿日期: 2024-11-27

  修回日期: 2025-03-17

  网络出版日期: 2025-04-09

收起

Reserve utilization evaluation model for tight gas well based on low-velocity non-Darcy seepage

  • Zechuan WANG , 1, 2 ,
  • Leng TIAN , 1, 2 ,
  • Jinbu LI 3 ,
  • Peng LI 3 ,
  • Xiaolong CHAI 1, 2 ,
  • Xiaojiao DENG 4 ,
  • Lili JIANG 1, 2
Expand
  • 1. College of Petroleum Engineering，China University of Petroleum （Beijing），Beijing 102249，China
  • 2. Research Center for Natural Gas Geology and Engineering，China University of Petroleum （Beijing），Beijing 102249，China
  • 3. Exploration and Development Research Institute，PetroChina Changqing Oilfield Company，Xi'an 710018，China
  • 4. PetroChina Oil，Gas and New Energy Company，Beijing 100007，China

Received date: 2024-11-27

  Revised date: 2025-03-17

  Online published: 2025-04-09

Supported by

The Key Applied Scientific and Technological Special Project of the China National Petroleum Corporation(2023ZZ25)

Fold

摘要

在致密气井衰竭开采中，随着地层压力下降，近井到远井地带的生产压力梯度逐渐降低，低速非达西渗流对生产的影响程度增加，为动用储量评价带来了挑战。通过室内实验，研究了致密含水岩石中不同孔隙压力下的气相低速非达西渗流现象，并以压裂水平井为例，建立了基于双重介质渗流表征的储量动用评价模型，量化描述了衰竭开采中动用储量及动用范围内采出程度的变化规律，进而探究了不同增产措施的影响。结果表明：①在运动方程中考虑低速非达西渗流能够更精确地描述气体流量随压差的非线性变化特征，从而使建立的数值模拟模型对储量动用的评价更加准确。②随着单井衰竭开采的进行，虽然储量动用范围不断扩大，但会导致对储量的控制程度不足，动用范围内的采出程度呈现先上升后下降的趋势，当气井开采达到采出程度最大值后，动用范围内的采出程度下降可达6%以上。③从提高动用储量采出程度的角度考量，增产措施重要性排序为：缩短裂缝间距>增加裂缝半长>提高裂缝导流能力>提高井底流压。降低井底流压及废弃产量虽然能够提高动用储量及累计产量，但会降低采出程度，人工压裂能兼顾增加单井动用地质储量与提高采出程度，是提升致密气井开采效率的主要方式。

关键词： 致密砂岩气藏; 低速非达西渗流; 压裂水平井; 动用储量; 采出程度

本文引用格式

王泽川 , 田冷 , 李进步 , 李鹏 , 柴晓龙 , 邓小娇 , 蒋丽丽 . 基于低速非达西渗流的致密气井储量动用评价模型[J]. 天然气地球科学, 2025 , 36(6) : 1000 -1011 . DOI: 10.11764/j.issn.1672-1926.2025.03.008

Abstract

In the depletion production process of tight gas wells， as the formation pressure declines， the production pressure gradient from the near-well region to the far-well region gradually diminishes. Meanwhile， the influence of low-velocity non-Darcy seepage on production becomes more pronounced. These dynamics complicate the evaluation of reserve utilization. In this work， through laboratory experimentation， the phenomenon of low-velocity non-Darcy seepage of gas under different pore pressures in tight water-bearing rocks is investigated. Using fractured horizontal wells as an example， a reserve utilization evaluation model based on dual-porosity seepage characterization is established. The variation law of reserve utilization and the recovery factor within the drainage area during the depletion process are quantitatively depicted， and the impact of different stimulation measures is probed. The results indicate that： （1） Incorporating the low-velocity non-Darcy seepage into the motion equation enables a more precise description of the nonlinear variation characteristics of gas flow with respect to the pressure difference. As a consequence， the established numerical simulation model can assess the dynamic reserves utilization with higher accuracy. （2） During the progression of single-well depletion production， the scope of exploited reserves expands. However， this expansion may result in inadequate reserve control. The recovery degree within the utilized scope initially exhibits an upward trend and subsequently a downward one. When the gas-well mining attains the maximum recovery factor， the recovery factor within the utilized scope decreases by over 6%. （3） From the perspective of enhancing the recovery degree of reserve utilization， the significance of stimulation measures can be ranked in the following order： shortening the fracture spacing > increasing the fracture half-length > improving the fracture conductivity > enhancing the bottom-hole flowing pressure. Lowering the bottom-hole flowing pressure and abandoned production condition can increase the reserve utilization and cumulative production； however， this will decrease the produced degree. Artificial fracturing is capable of increasing both the geological reserve utilization and the produced degree of a single well， which represents the primary approach to improving the mining efficiency of tight-gas wells.

Key words： Tight sandstone gas reservoir; Low-velocity non-Darcy seepage; Fracturing horizontal well; Reserve utilization; Recovery factor

0 引言

致密砂岩气是全球开发规模最大的非常规天然气之一，我国致密气具有巨大的资源潜力和可观的规模储量，目前致密气已成为我国产气量最大的气藏类型［1-2］。然而，以苏里格为代表的致密气藏目前采出程度不足15%［3］，已开发区域仍有很大地提高采收率的空间。确定单井储量动用情况是气藏开发评价的重要工作，对井网加密、增产措施方案的制定具有重要意义［1-4］。
对于连续聚集和分布的致密气藏［5-7］，单井动用储量评价的关键是确定动用范围大小及动用范围内的压力分布情况［8］。前人［8-12］通过长岩心多点测压衰竭开发实验，对储量动用规律开展了大量研究，量化分析了含水饱和度、渗透率、废弃产量等因素对采出程度的影响，但室内实验所用岩心尺寸有限，对压力剖面、储量分布等研究的尺度较小，在矿场应用中存在局限性。针对气井储量动用的评价方法包括物质平衡法、弹性二相法和产量递减法等［13-15］，但这些方法需要基于试井数据或对产量的长期监测，且无法研究衰竭开发中的单井动用储量及动用范围内采出程度的变化规律。
随着计算机科学的发展，数值模拟技术在气藏开发中得到了大规模应用［16-17］，它能够对动用储量和可采储量进行更精细的描述。然而，在致密含水储层中，气相渗流规律与常规储层相比展现出很大的差异，如启动压力梯度现象、低速非达西渗流特征等［18-20］。前人［21-22］虽然针对渗透率、含水饱和度等因素对启动压力梯度的影响开展了大量实验研究，但对衰竭开发中孔隙压力变化下的气相非线性渗流规律的研究却鲜有披露。且现有模型大多关注致密气藏中的特殊渗流机理对气井产能的影响［23-25］，而对低速非达西渗流下的储量动用规律缺乏深入的认识。
在气藏衰竭开发中，随着地层压力下降，近井到远井地带的生产压力梯度逐渐降低，低压非线性渗流对生产的影响程度增加，且由于致密储层大都需要进行压裂作业，不同的储层改造及增产措施为致密含水气藏中储量动用范围及采出程度的确定带来了新的挑战。本文通过室内实验，研究了致密含水岩石中不同孔隙压力下的气体低速非达西渗流现象，进而以压裂水平井为例，在双重介质气水两相数值模拟的基础上，明确了气井衰竭开采时动用储量和动用范围内采出程度的变化规律，并探究了不同增产措施的影响，实现了对储量动用效果的量化评价。

1 低速非达西渗流实验

本实验采用背压系统，研究衰竭过程中不同压力、压差下的气相流动特征。
从鄂尔多斯盆地苏中地区一口取心井中选取盒8段的典型致密砂岩岩心，岩心长度为7.85 cm，直径为2.44 cm，按照国家标准《岩心分析方法》（GB/T 29172—2012），测定其孔隙度为6.5%，渗透率为0.186×10-3 μm2。润湿性测试表明该岩心为强水湿，有着非常良好的亲水性。探究低速非达西渗流规律的实验装置示意图如图1所示，主要实验步骤如下：
图1 低速非达西渗流实验装置图

Fig.1 Device diagram of low-velocity non-darcy seepage experiment

（1）将岩心抽真空后饱和地层水并称重。
（2）将岩心放入加持器中并施加围压，接着利用驱替泵进行气驱，从而建立岩心中的含水饱和度为39.2%。
（3）在含水岩心中开展气相非线性渗流实验，为了模拟真实气藏衰竭开发的降压过程，将围压保持为40 MPa，温度设置为80 ℃，首先用高压驱替泵在岩心中充入氮气气体，并调节回压阀使岩心中保持30 MPa孔隙压力。
（4）改变入口端压力，在低压差下开展气驱实验，待压力及出口端气流量稳定后记录出入口端压力及气流量，接着缓慢增大压差，得到完整的流量曲线。
（5）调节回压阀，改变岩心中的孔隙压力，得到不同压力下的气流量曲线。
为了保证岩心中的气体呈现单相流动特征，在实验过程中需要缓慢变化压力及压差，避免岩心中的水相被驱出。在实验前后对岩心分别进行称重并计算含水饱和度，使实验前后的含水饱和度偏差不大于2%，否则需要重新进行实验。
在实验后通过以下公式计算气体在不同压力、不同压差下的视渗透率：
K a p p = 2 P 0 Q 0 μ L A ( P 1 2 - P 2 2 )
式中：K app为气体的视渗透率，m2；A为岩样截面积，m2；L为岩样长度，m；P 1、P 2分别为进、出口端压力，Pa；P 0为大气压力，1×105 Pa；μ为气体黏度，Pa·s；Q 0为大气压下的气体流量，m3/s。

2 动用储量评价模型

2.1　非线性渗流规律表征

室内实验虽然能在一定程度上反映岩石渗流规律，但由于岩心尺寸较小，无法完全代表地下大范围的储层特征。针对实际地层中的流体流动，达西定律被广泛用于描述岩石中的流体渗流速度与压力降之间的关系（图2），对气相的运动方程可写为：
v g m = - K m k r g μ g ∇ p m
式中：v gm为气体流速，m/s； K m为岩石绝对渗透率，m2； k r g为气体相对渗透率； μ g为气相黏度，Pa·s； ∇ p m为压力梯度，Pa/m。
图2 流速曲线示意

Fig.2 Flow velocity curve diagram

相比于常规储层中的达西渗流，在致密含水储层中，气体流量在高压力梯度下线性趋势的反向外推并不经过原点，此时传统的达西定律已不再适用（图2）。部分学者在渗流方程中加入拟启动压力梯度（PTPG）来表征这种低速渗流现象［24-27］，其运动方程被如下表示。
v g m = 0          ∇ p m ≤ λ - K m k r g μ g ∇ p m - λ        ∇ p > λ
式中： λ为气相流动的拟启动压力梯度，Pa/m。
虽然对运动方程的改进在实际应用中取得了较好的效果，然而，因为 λ体现的是储层中的拟启动压力梯度（图2），该方程的实质是对低速非达西渗流的一种近似描述，它高估了气相流动的启动压力梯度［28］。在致密气井的衰竭开采前期，泄流面积相对较小，生产压力梯度大，在运动方程中加入拟启动压力梯度的方法能够取得较好的预测及评价效果。然而，当开采进入中后期，随着泄流面积的增大，从远井地带到近井地带的生产压力梯度减小，该等效方法对渗流规律的数学描述与实际状况偏差较大，导致对地层中储量动用情况难以准确评价。因此，考虑气相在低压下的非线性流动特征是十分必要的。
针对致密储层中流体低速非线性流动现象，应用经验公式进行数学化拟合是一种常用方法，依据XU等［28-29］提出的非线性方程对低速非达西渗流规律进行表征，从而使气相的运动方程被写为：
v g m = 0                                                          ( ∇ p m ≤ G g ) - K m k r g μ g 1 - b + G g b + | ∇ p m | ∇ p m   ( ∇ p m > G g )
式中：G g为气相的实际启动压力梯度，Pa/m；b为系数，需要通过对实验数据进行拟合得到。

2.2　考虑低速非达西的压裂水平井储量动用评价模型

针对层状连续分布的致密气藏，部署水平井并采用分段压裂是一种有效的开发方式，虽然针对压裂水平井的产能评价模型已有较多研究［30-32］，但针对其储量动用特征的研究却鲜有报道。本文在非线性渗流规律表征的基础上，以分段压裂水平井为例，探究在生产过程中的储量动用及采出程度的变化，考虑储层基质和裂缝间显著的渗透率差异［33-34］，应用双重介质模型对气水在储层中的渗流状况进行描述，并建立相应的数值模拟方法。

2.2.1　模型假设

所建立的物理模型如图3所示，其基于以下假设：
图3 压裂水平井物理模型

Fig.3 Fracturing horizontal well physical model diagram

（1）储层中存在气水两相流体的等温流动，且不存在传质作用，不考虑重力的影响。
（2）有限导流的人工裂缝垂直于水平井筒，且缝高与储层厚度相等，近井地带的流体能够直接流入井筒，而对于远井地带，基质中的流体会优先向裂缝汇聚，进而流入水平井筒。
（3）忽略表皮效应及井筒储集现象，裂缝系统只作为流动通道，即 ϕ f = 0。
（4）致密气藏主要依靠气体的膨胀能量进行衰竭开采，因此忽略水和岩石压缩性对孔隙体积的影响。

2.2.2　数学模型

（1）基质系统
在致密储层中，渗透率的应力敏感现象严重［35］，因此在非线性渗流运动方程［式（4）］的基础上，考虑衰竭开发中渗透率随压力的变化关系如下：
K m p m = K m i e - α m ( p i - p m )
式中：K mi为原始地层压力下的渗透率，m2；p m为地层压力，Pa； α为应力敏感系数，可以通过对实验数据进行拟合获得。
综上，致密含水气藏衰竭开发中，受地层压力和流动压力梯度影响的气相渗透率可被修正为：
k g , a p p ( p m , ∇ p m ) = 0                                                                   ∇ p m ≤ G g K m p m k r g 1 - b + G g p m b + | ∇ p m |            ∇ p m > G g
对水相的运动方程可写为：
v w m = - K m p m k r w μ w ∇ p m
式中：v wm为水在岩石基质中的流速，m/s； k r w为水相对渗透率； μ w为水黏度，Pa·s；
对岩石基质，气水两相的连续性方程为：
- ∇ ρ g ν g m + q g m = ∂ ϕ ρ g S g ∂ t
- ∇ ρ w ν w m + q w m = ∂ ϕ ρ w S w ∂ t
式中：q gm、q wm分别为流出基质的气、水质量流量，kg/s； ρ g、 ρ w分别为气、水两相的密度，kg/m3；S g、S w分别为气、水两相的饱和度； ϕ为岩石孔隙度，小数。
（2）裂缝—井筒系统
在致密储层中，相对于岩石基质，裂缝的导流能力明显更强，渗流规律符合达西渗流［32-34］，因此气水两相的运动方程可写为：
ν g f = - K f K r g μ g ∇ p f
ν w f = - K f K r w μ w ∇ p f
式中：v gf、v wf分别为气、水在裂缝中的流速，m/s；K f为裂缝渗透率，m2； ∇ p f为裂缝中的压力梯度，Pa/m。
由于裂缝仅作为流动通道，不作为储存流体的空间，因此连续性方程为：
- ∇ ρ g ν g f - q g f = 0
- ∇ ρ w ν w f - q w f = 0
式中：q gf、q wf分别为流入裂缝的气、水质量流量，kg/s；
考虑水平井开发时井筒内摩阻为［36］：
Δ p w j = 2 f o h   ρ π 2 D 5 2 Q j + q j 2 Δ x + 16 ρ q j π 2 D 4 2 Q j + q j
式中： f o h  为井筒内摩擦阻力系数； ρ为流体密度，kg/m3；D为井筒直径，m；Qj 为水平井第j段沿轴向流量，m3/s；qj 为水平井第j段的径向流量，m3/s。
（3）附加方程
由于气体的压缩性远高于流体，气体密度会随压力发生显著变化，真实气体的状态方程可写为：
ρ g = m V = M g p g Z R T
式中：Z为偏差因子；R为理想气体常数；T为温度，K；p g为气体压力，Pa。
饱和度方程：
S g + S w = 1
（4）边界及初始条件
对衰竭开发的储层，地层压力的初始条件为：
p ( x , y ) t = 0 = p i
S w t = 0 = S w i
式中：P i为原始地层压力，Pa；S wi为地层初始含水饱和度。对于采用逐级降压方式生产的水平井，其内边界条件可写为：
p w f ( x i , y i , t ) = p w f t
式中： p w f ( t )为水平井跟端的井底压力，Pa。
在无外界能量补充的条件下，封闭外边界条件可表示为：
∂ p ∂ x x = a = 0 ∂ p ∂ y y = b = 0
（5）储量动用计算方法
对单井而言，动用储量可以表示为实时动用范围内的地质储量［15］，根据容积法，对致密气井而言，实时动用储量可以由下式计算［13］：
R g t = A g ( t ) h ϕ S g i 1 B g i
式中： R g t为单井实时生产时的动用储量，m3； A g ( t )为动用范围的面积，m2；h为储层厚度，m；S gi为原始含气饱和度；B gi为原始天然气体积系数。
单井衰竭开采时，动用范围内的采出程度可由下式表示：
η ( t ) = C g t R g t
式中： C g t为累计采出的气量，m3； η ( t )为动用范围内的采出程度。

2.2.3　模型求解

联立公式（4）—（20），即可建立针对致密气藏中压裂水平井衰竭开采的渗流数学模型。在应力敏感及低速非达西渗流的影响下，储层的渗透率具有时变性，因此该模型难以得到解析解，研究中应用有限差分法对数学模型进行离散化处理。为了兼顾求解结果的准确性和稳定性，选择了隐式求解压力，显式求解饱和度的半隐式求解方法。进而借助编程手段，利用时间步进迭代法，将生产过程按月划分为多个时间步，在每个时间步内根据当前的状态计算下一时刻的地层压力分布、产气量等关键参数。通过不断迭代，可以得到不同时刻的气井生产动态，从而建立了针对分段压裂水平井生产动态的数值模拟方法。在此基础上，依据式（21）—式（22），可以对单井生产中压力传播范围内的储量动用及采出程度进行计算。

3 结果与讨论

3.1　低速非达西渗流实验表征

如图4所示为不同孔隙压力和不同压力梯度下的气体流量曲线，可以看到，在低压力梯度下，气体展现出一种非线性的流动特征，即气体流量并不随平方压力梯度的增加而线性增加，这一变化趋势与前人［21-23］所得到的实验结果相一致。
图4 流量—平方压力梯度曲线

Fig.4 Flow and square pressure gradient relationship curve

图5展示了在不同压力和压差下的气相视渗透率，在较低的压差下，气体视渗透率会随压差的增加而呈凸形曲线增大，逐渐增加到最大视渗透率。同时，随着孔隙压力的降低，由于岩石受到的有效应力增大，气体渗透率降低，启动压力梯度增加，达到最大视渗透率所需的压力梯度也显著增加。主流观点认为［21-22］，在贾敏效应的影响下，气体流动压力梯度的增大可以使更多的孔喉参与流动，提高气相的渗透率，从而使流动曲线呈现凹形特征，而当压力梯度达到一定界限时，参与流动的孔喉数量趋于稳定，曲线也趋于直线，此时气体的渗透率不再增加。应用公式（6）对不同压力、压差下的气相渗透率实验数据进行拟合，从结果来看（图5），实验数据与公式拟合的结果较好，通过对达西公式进行修正能够更好地表征含水储层中的气相渗流规律。
图5 视渗透率—压差曲线

Fig.5 Relationship curve between apparent permeability and pressure difference

3.2　模型验证

某水平井位于鄂尔多斯盆地伊陕斜坡苏里格地区，于2019年5月完钻，开采层位为盒8段，该区域砂体连续性及气体充注效果好，平均水气比为0.5 m3/104 m3，属于低产水气井，经过了近4年的开采，该井日产气量降至初期的20%以下。为了分析单井储量动用特征，建立了针对单井渗流的数值模拟模型，主要模拟参数如表1所示。在此基础上，将实时的井底流压作为模型的输入数据，从而计算单井的动态产气量。实际生产数据和模型计算数据对比如图6所示。
表1 数值模拟参数统计

Table 1 Statistical table of numerical simulation parameters

项目 数值
模拟地质模型长度/m 1 170
模拟地质模型宽度/m 675
原始地层压力/MPa 27
含水饱和度/% 39
渗透率/（10-3 μm2） 0.193
孔隙度/% 6.83
地层系数/（10-3 μm2·m） 5.65
井筒水平段长/m 670
砂体钻遇率/% 97
压裂方式 分段压裂
裂缝条数/条 5
裂缝方向（相对井筒） 横向
裂缝导流能力/（10-3 μm2·m） 30
图6 生产数据拟合图

Fig.6 Production data fitting diagram

利用相对平均绝对误差（RMAE）量化模型计算结果和实际生产数据之间的差异［37］。计算方法表示如下：
R M A E = ∑ i = 1 m y i - y ^ i m y ¯
式中： y i为模型的计算结果； y ^ i代表实际生产数据； y ¯代表实际生产数据的平均值；m 代表实际生产数据的样本点数。
计算表明，两者的相对平均绝对误差为4.12%，模型计算得到的产气数据与实际产量的变化趋势吻合度较好。而在单井的压力传播范围内，应用公式（21）计算得到动用储量为10 206×104 m3。同时，依据现场试井资料，用物质平衡法分析该井目前控制的地质储量为9 885×104 m3，两者误差在5%以下，显然，该数值模拟模型对动用储量的评价较为准确。

3.3　不同渗流模式下的储量动用对比

在气井开采时，由于远井到近井地带的储层中存在压力差，气藏中的压力呈现倒锥状漏斗分布，在单井动用范围内的地质储量并不会被全部采出。通过对运动方程进行修改，能够表征达西渗流、低速非达西渗流、仅考虑启动压力梯度3种渗流模式。在应用上述单井参数开展数值模拟的基础上，设置生产制度为相同的井底流压，模拟5年后的压力分布如图7所示。
图7 不同渗流模式下的压力分布

（a）达西渗流；（b）考虑拟启动压力梯度；（c）低速非达西渗流

Fig.7 Pressure distribution with different seepage modes

为了对比描述不同渗流模式对动用储量及采出程度的影响，在数值模拟的基础上，应用公式（21）—式（22），对压力传播区域内的动用储量和采出程度进行了计算，其结果如表2所示。
表2 不同渗流模式下的储量动用统计

Table 2 Statistics table of reserve utilization with different seepage modes

渗流模式 动用储量/（104 m3） 采出量/（104 m3） 动用范围内采出程度/%
达西渗流 24 551 5 731 23.3
仅考虑拟启动压力梯度 9 802 3 567 36.4
考虑低速非达西渗流 11 701 3 639 31.1
对气藏而言，地层中的压力分布能够反映储量动用情况［36］，可以看到，在达西渗流模式下［图7（a）］，生产井周边压力传播范围均匀，呈现椭圆流动特征，计算动用储量高达24 551×104 m3，相比于考虑低速非达西渗流计算的动用储量高出了1倍以上；达西渗流模式下的计算采出量为5 731×104 m3，相比于考虑低速非达西渗流的3 639×104 m3高出了1/3以上，但动用范围内的采出程度却较低。这是由于达西渗流忽略了非线性渗流和启动压力梯度的影响，过分高估了致密含水储层中的气相渗流能力（图2），从而导致了计算动用储量和采出量的严重失真。
当在运动方程中考虑了拟启动压力梯度时，由于压力的传播范围会受到拟启动压力梯度的限制，因此出现了很明显的压力分布不均的现象［图7（b）］，在远离井筒和裂缝的区域产生了更多的剩余气。仅考虑拟启动压力梯度条件下的计算动用储量为9 802×104 m3，相比于考虑低速非达西渗流计算得到的动用储量为11 701×104 m3，低了15%以上，这是由于等效处理后的拟启动压力梯度相比于气相实际启动压力梯度明显更大（图2）。另外，仅考虑拟启动压力梯度条件下的动用范围内采出程度被计算为36.4%，而考虑低速非达西渗流计算得到的动用范围内采出程度为31.1%。这是由于在采出量差距不大的情况下，仅考虑拟启动压力梯度会低估气井的控制范围，从而高估了动用范围内的采出程度。对比而言，本文建立的考虑低速非达西渗流的数值模拟方法，在表征了气相真实启动压力梯度的同时，对气相在低流速下的非线性渗流规律也进行了描述，因此对动用储量和采出程度的估计更加准确。

3.4　衰竭开发动用储量变化规律

对单井而言，井控储量指单井控制范围内的地质储量，它取决于井控范围，部分学者利用物理模拟实验与数学评价相结合的方法，对井控范围进行探究［38-39］，或者用启动压力梯度进行估算［15］，然而，当气井开采进入中后期，由于储层物性差，部分远井地带的被控制储量并不能被高效采出。目前对致密气藏水平井生产中的实时储量动用范围已有较多研究［40-41］，但对动用范围内采出程度的变化规律研究却鲜有披露，尤其在致密气藏中渗流阻力大，将动用范围内的储量转化为可采储量更加困难。为了研究衰竭开发中的动用储量变化规律，利用已建立的数学模型，在单井生产动态拟合的基础上，计算了动用储量、采出量以及动用范围内采出程度的动态变化如图8所示。
图8 衰竭开发中储量动用变化

Fig.8 Change of reserve utilization in the depletion development

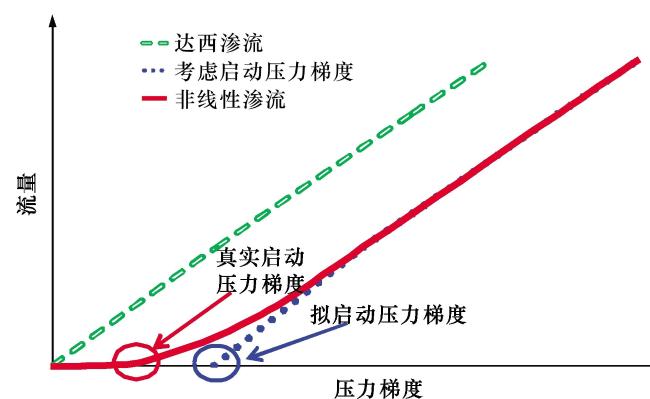
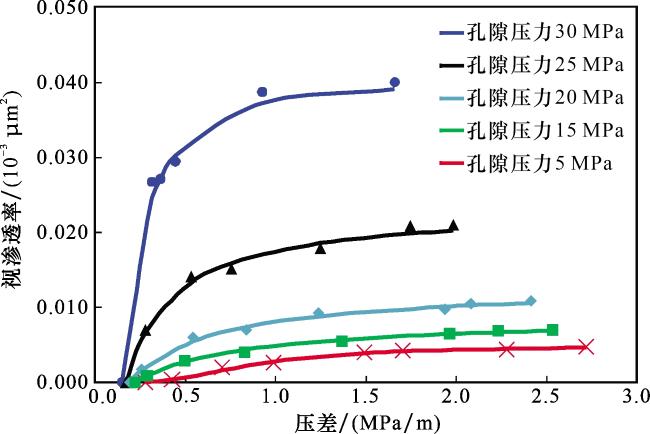
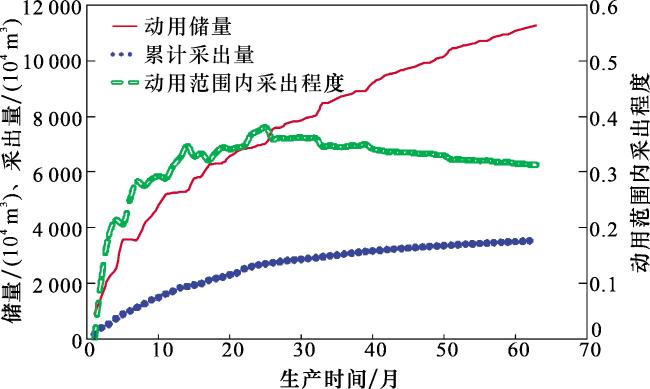
在气井衰竭开采的过程中，随着压力的不断传播，储量动用范围不断扩大，然而，由于致密储层渗流阻力大，且气体存在非达西渗流现象，在低压差下的渗透率会进一步降低（图5），气井产能下降，累计产量曲线也逐渐趋于平缓，气井动用范围内的采出程度呈现先上升后下降的趋势。显然，仅用井控储量可能会高估单井对地质储量的控制程度，若从优化采出程度的角度考量，单井对动用储量的控制存在最优值，以此单井为例，开采2年后的动用储量为7 000×104 m3，累计产量为2 700×104 m3，剩余储量为4 300×104 m3，此时动用范围内采出程度达到最大值为38%。此后开采的四年时间中，虽然动用储量增加至11 300×104 m3，增幅达1/2以上，但由于气井产能不足，累计产量仅增加近800×104 m3，增幅在1/3以下。同时，在此期间，动用范围内的剩余储量由4 300×104 m3增至7 800×104 m3，增幅超过80%，由此导致动用范围内的采出程度也下降至31%。显然，废弃产量的降低虽然能够延长气井开采寿命，增加动用储量，但由于致密储层中的渗流阻力大，单井对动用储量的控制不足，导致动用范围内采出程度下降6%以上。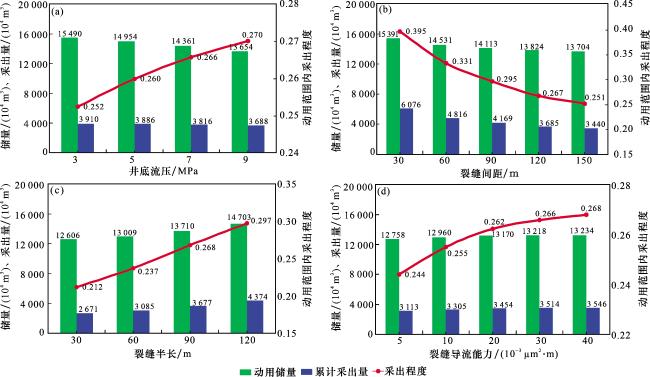从压力分布图中可以看到［图7（c）］，越靠近井筒及裂缝处的压力越低，采出程度越高，因此，采用井网加密的方法能够有效提高采出程度，然而，具体的加密界限还需要结合经济评价进一步探究［3， 42］。

3.5　敏感性分析

虽然采用储层改造、生产制度调整等方式能够提高单井产量，但对储量动用及采出程度的影响尚不明确。本文应用已建立的数值模拟方法，对采用不同措施生产的分段压裂水平井分别进行了10年的生产模拟，并对比分析了多因素影响下的储量动用及采出情况。

3.5.1　井底流压

在致密气藏衰竭开发中，降低井底流压是常见的增产方式，图9（a）对比了不同井底流压下的储量动用及采出程度，可以看到，当井底流压从9 MPa下降至3 MPa，储量动用程度及累计采出量均有增加，但动用范围内的储量采出程度降低。采出程度随井底压力的变化曲线呈现凸形特征，即单位井底压力下降时的采出程度降低幅度呈增加趋势，单井对动用范围内储量的控制效果进一步变差。
图9 不同因素对储量动用的影响

（a）井底流压；（b）裂缝间距；（c）裂缝半长；（d）裂缝导流能力

Fig.9 Influence of different factors on reserve utilization

3.5.2　裂缝间距

裂缝间距是分段压裂水平井非常重要的设计参数［42-43］。其对储量动用及采出程度的影响如图9（b）所示。模拟结果表明，虽然储量动用受裂缝间距的影响相对较小，但裂缝间距的增加会显著降低动用范围内的采出程度，当裂缝间距由30 m增加至150 m时，采出程度下降了10%以上，这是由于在致密储层中气相存在低速非达西流动现象，大间距裂缝对储量的控制程度不足，容易出现更多的剩余气。因此在分段压裂中采用裂缝加密的方式有利于提高单井动用储量范围内的采出程度。

3.5.3　裂缝半长

图9（c）对比了不同裂缝半长下的储量动用及采出程度，当裂缝半长由30 m增加至120 m，动用储量增加了10%以上，累计产量的增幅在30%以上，而采出程度增加了8%以上。其主要原因在于裂缝半长的增加能够为气体流动提供“高速通道”，渗流阻力的减小使储层中的生产压力梯度降低，从而提高了动用范围内的采出程度。

3.5.4　裂缝导流能力

不同裂缝导流能力对储量动用及采出的影响对比如图9（d）所示，当裂缝导流能力由5×10-3 μm2·m提升至40×10-3 μm2·m时，动用储量增加幅度在4%以下，采出程度仅提升2.4%左右，影响程度相对较小，且随着裂缝导流能力的增加，采出程度的上升趋势逐渐变缓。这是因为致密储层中的流体储集和流动会受到基质的制约，裂缝导流能力的增加虽然能够降低储层中的流体渗流阻力，但对提高动用储量及采出程度的影响有限。
从数值模拟结果来看，不同增产措施对储量动用及采出程度的影响程度存在显著差异，若从提高单井动用地质储量的角度考量，不同增产措施的主次顺序为增加裂缝半长>降低井底流压>缩短裂缝间距>提高裂缝导流能力，然而，随着动用范围的扩大，单井对动用范围内储量可能存在控制不足的情况，比如井底流压的降低会导致单井对储量的控制程度减弱。而从提高采出程度方面来看，不同增产措施的重要性排序依次为缩短裂缝间距>增加裂缝半长>提高裂缝导流能力>提高井底流压。因此，利用人工压裂的方式能够在增加单井动用地质储量的同时提高动用范围内的采出程度，是提高致密气井开采效率的主要方式。

4 结论

（1）通过开展室内实验，发现致密含水储层中的气体在低压差下的流量曲线呈非线性特征，随着孔隙压力的降低，有效应力增大，低速非达西渗流现象更加明显。
（2）基于对运动方程的改进，建立了考虑气相低速非达西渗流的数值模拟模型，计算得到的单井生产动态与实际生产吻合度高，验证了模型的可靠性，相比于达西渗流及仅考虑启动压力梯度的渗流模型，新建立模型能够更精确地描述气体流量随压差的非线性变化特征，对储量动用及采出程度的评价更加准确。
（3）在单井衰竭开采的过程中，随着压力的传播，实时动用储量不断增加，然而，由于致密储层渗流阻力大，且气体存在低速非达西渗流现象，气井难以对动用范围内的储量进行有效控制，在产能降低的同时，储量动用范围内的采出程度呈现先上升后下降的趋势。
（4）采取不同增产措施对储量动用及采出程度的影响存在差异，降低井底流压及废弃产量能够提高储量动用程度及累计产量、但会降低动用范围内的采出程度；缩小裂缝间距、增加裂缝半长及导流能力可以有效提高动用地质储量及动用范围内的采出程度。因此，储层改造是提高致密气井开采效率的主要方式。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
1
贾爱林，位云生，郭智，等.中国致密砂岩气开发现状与前景展望［J］.天然气工业，2022，42（1）：83-92.

JIA A L，WEI Y S，GUO Z，et al.Development status and pro-spect of tight sandstone gas in China［J］.Natural Gas Industry， 2022， 42（1）： 83-92.

2
辜穗，王文婧，高琼，等.致密砂岩气规模效益开发管理机制［J］.天然气工业，2023，43（5）：100-107.

GU S， WANG W J， GAO Q， et al. Management mechanism of large-scale benefit development of tight sandstone gas［J］. Natural Gas Industry， 2023， 43（5）： 100-107.

3
马新华，何东博，位云生，等.天然气提高采收率理论基础、技术方法与发展方向［J］.天然气工业，2023，43（1）：1-12.

MA X H， HE D B， WEI Y S， et al. Enhanced gas recovery： Theory，technology and prospect［J］.Natural Gas Industry，2023，43（1）：1-12.

4
付斌，李进步，张晨，等.强非均质致密砂岩气藏已开发区井网完善方法［J］.天然气地球科学，2020，31（1）：143-149.

FU B， LI J B， ZHANG C， et al. Improvement of well pattern in development area of tight sandstone gas reservoir［J］.Natural Gas Geoscience， 2020， 31（1）： 143-149.

5
贾承造，庞雄奇，宋岩.论非常规油气成藏机理：油气自封闭作用与分子间作用力［J］.石油勘探与开发，2021，48（3）：437-452.

JIA C Z， PANG X Q， SONG Y. The mechanism of unconventional hydrocarbon formation：Hydrocarbon self-containment and intermolecular forces［J］.Petroleum Exploration and Development，2021，48（3）：437-452.

6
邹才能，杨智，董大忠，等.非常规源岩层系油气形成分布与前景展望［J］.地球科学，2022，47（5）：1517-1533.

ZOU C N，YANG Z，DONG D Z，et al.Formation distribution and prospect of unconventional hydrocarbons in source rock strata in China［J］.Earth Science，2022，47（5）：1517-1533.

7
戴金星，董大忠，倪云燕，等.致密砂岩气藏与页岩气藏展布模式［J］.石油勘探与开发，2024，51（4）：667-678.

DAI J X， DONG D Z， NI Y Y， et al. Distribution patterns of tight sandstone gas and shale gas［J］.Petroleum Exploration and Development， 2024， 51（4）： 667-678.

8
张杰，李熙喆，高树生，等.致密砂岩气藏产水机理及其对渗流能力的影响［J］.天然气地球科学，2019，30（10）：1519-1530.

ZHANG J，LI X Z，GAO S S，et al.Water production mechanism of tight sandstone gas reservoir and its influence on percolation capacity［J］.Natural Gas Geoscience，2019，30（10）：1519-1530.

9
胡勇，焦春艳，王继平，等.含水致密砂岩气藏储量动用规律实验［J］.大庆石油地质与开发，2021，40（4）：154-161.

HU Y， JIAO C Y， WANG J P， et al. Experiment on the reserves producing law for water-bearing tight sandstone gas reservoirs［J］.Petroleum Geology & Oilfield Development in Daqing，2021，40（4）：154-161.

10
江良冀，王国锋，胡勇，等.含水砂岩气藏储量动用分级评价实验［J］.天然气地球科学，2023，34（7）：1137-1145.

JIANG L J，WANG G F，HU Y， et al. Experiment on production classification evaluation of water-bearing sandstone gas reservoirs［J］. Natural Gas Geoscience， 2023， 34（7）： 1137-1145.

11
李进步，王继平，李娅，等.致密砂岩气藏逐级降压开采物理模拟实验认识与启示［J］.天然气工业，2022，42（1）：125-132.

LI J B，WANG J P，LI Y，et al.Physical simulation experiment of step-by-step depressurization production of tight sandstone gas reservoirs：Understanding and revelation［J］.Natural Gas Industry， 2022， 42（1）： 125-132.

12
胡勇，李熙喆，卢祥国，等.砂岩气藏衰竭开采过程中含水饱和度变化规律［J］.石油勘探与开发，2014，41（6）：723-726.

HU Y，LI X Z，LU X G，et al. Varying law of water saturation in the depletion-drive development of sandstone gas reservoirs［J］.Petroleum Exploration and Development，2014，41（6）：723-726.

13
气藏工程编写组. 气藏工程［M］.北京：石油工业出版社， 2017.

Gas Reservoir Engineering Compilation Group.Gas Reservoir Engineering［M］.Beijing：Petroleum Industry Press，2017：179-188.

14
王晨辉，贾爱林，位云生，等.单井和区块动储量评估方法优选及应用——以某断块小气藏为例［J］.天然气地球科学，2024，35（4）：585-595.

WANG C H，JIA A L，WEI Y S，et al.Comparisons and application of single well and reservoir dynamic reserves evaluation methods：Case study of a small fault block gas reservoir［J］. Natural Gas Geoscience，2024，35（4）：585-595.

15
陈占军，任战利.致密砂岩气藏单井动用地质储量和技术可采储量计算方法——以鄂尔多斯盆地延长气田石炭系一二叠系气藏为例［J］.新疆石油地质，2022，43（3）：360-367.

CHEN Z J， REN Z L. Method for calculating single-well producing geological reserves and single-well technically recoverable reserves in tight sandstone gas reservoirs：A case of carboniferous-permian gas reservoirs in Yanchang Gas Field，Ordos Basin［J］.Xinjiang Petroleum Geology，2022，43（3）： 360-367.

16
杨东升，谢坤，殷庆国，等.边底水气藏水侵规律研究现状与展望［J］.天然气地球科学，2024，35（7）：1304-1322.

YANG D S，XIE K，YIN Q G，et al. Research status and prospect of water intrusion law in edge and bottom water gas reservoirs［J］.Natural Gas Geoscience，2024，35（7）：1304-1322.

17
马志欣，吴正，李进步，等.河流相致密砂岩气藏剩余气精细表征及挖潜对策——以苏里格气田中区SSF井区为例［J］.天然气工业，2023，43（8）：55-65.

MA Z X， WU Z， LI J B， et al. Fine characterization and potential tapping countermeasures of remaining gas in fluvial tight gas reservoirs：A case study of the SSF well block in central Sulige Gas Field［J］.Natural Gas Industry，2023，43（8）：55-65.

18
HE Y， WANG J J， HUANG X Q， et al. Investigation of low water recovery based on gas-water two-phase low-velocity Non-Darcy flow model for hydraulically fractured horizontal wells in shale［J］. Petroleum， 2023， 9（3）： 364-372.

19
YAN N.Development of production decline curves for non-Darcy oil flow in low-permeability reservoirs［J］. Journal of Petroleum Science and Engineering， 2022， 218.

20
王苏冉，白玉湖，徐兵祥，等.致密砂岩气井气水两相产能预测半解析模型［J］.科学技术与工程，2022，22（21）：9105-9114.

WANG S R， BAI Y H，XU B X， et al. Semi-analytical model of production prediction for tight sandstone gas wells considering gas-water two phase flow behavior［J］. Science Technology and Engineering， 2022， 22（21）： 9105-9114.

21
DING J C，YANG S L，NIE X R， et al. Dynamic threshold pressure gradient in tight gas reservoir［J］. Journal of Natural Gas Science and Engineering， 2014， 20： 155-160.

22
ZAFAR A，SU Y L，LI L，et al. Tight gas production model considering TPG as a function of pore pressure，permeability and water saturation［J］.Petroleum Science，2020，17（5）：1356-1369.

23
TIAN W B， LI A F， REN X X， et al. The threshold pressure gradient effect in the tight sandstone gas reservoirs with high water saturation［J］. Fuel， 2018， 226： 221-229.

24
GENG S Y， LI C Y， LI Y， et al. Pressure transient analysis for multi-stage fractured horizontal wells considering threshold pressure gradient and stress sensitivity in tight sandstone gas reservoirs［J］.Gas Science and Engineering，2023，116：205030.

25
杨朝蓬，李星民，刘尚奇，等.苏里格低渗致密气藏阈压效应［J］.石油学报，2015，36（3）：347-354.

YANG Z P， LI X M， LIU S Q， et al. Threshold pressure effect of low-permeability tight gas reservoirs in Sulige Gas Field［J］.Acta Petrolei Sinica，2015，36（3）：347-354.

26
李恒，黄炳香，孙政，等.高效预测气藏产能的线化双重介质模型［J］.中国科学：物理学力学 天文学，2022，52（12）：131-144.

LI H，HUANG B X，SUN Z，et al. Efficient linear dual-medium model for production prediction（in Chinese）［J］.Science Sinica Physica，Mechanica & Astronomica，2022，52（12）：131-144.

27
SONG H Q，CAO Y，YU M X， et al. Impact of permeability heterogeneity on production characteristics in water-bearing tight gas reservoirs with threshold pressure gradient［J］.Journal of Natural Gas Science and Engineering，2015，22：172-181.

28
WANG X K， SHENG J. Discussion of liquid threshold pressure gradient［J］. Petroleum， 2017， 3（2）： 232-236.

29
XU J C， JIANG R Z， XIE L S， et al. Non-Darcy flow numerical simulation for low-permeability reservoirs［C］. SPE Europec featured at EAGE Conference and Exhibition， 2012： SPE-154890-MS.

30
陈福有，郝明强，陈美瑾，等.特低渗透油藏压裂水平井裂缝间距计算方法［J］.油气井测试，2016，25（3）：18-22，76.

CHEN F Y，HAO M Q，CHEN M J，et al. Calculation method for fracture spacing of fractured horizontal wells in ultra-low per-meability oil reservoirs［J］.Well Testing，2016，25（3）：18-22，76.

31
宋俊强，李晓山，王硕，等.致密油藏压裂水平井产量预测［J］.新疆石油地质，2022，43（5）：580-586.

SONG J Q， LI X S， WANG S， et al. Production prediction of fractured horizontal wells in tight oil reservoirs［J］.Xinjiang Petroleum Geology，2022，43（5）：580-586.

32
陈志明，Yu Wei，石璐铭，等.压裂水平井的多模式裂缝网络试井模型及参数评价——以吉木萨尔页岩油为例［J］.石油学报，2023，44（10）：1706-1726.

CHEN Z M， YU W， SHI L M， et al. Well test model and parameter evaluation of multi-mode fracture network in fractured horizontal well：A case study of Jimsar shale oil［J］. Acta Petrolei Sinica，2023，44（10）：1706-1726.

33
宋海敬，王云刚，邓勇，等.异常高压致密气藏两相渗流数值模拟技术［J］.科学技术与工程，2017，17（24）：204-208.

SONG H J， WANG Y G， DENG Y， et al. A flow numerical simulation technology on gas-water two phase in tight gas reservoirs with abnormally high pressure［J］. Science Technology and Engineering， 2017， 17（24）： 204-208.

34
罗红文，李海涛，刘会斌，等.低渗气藏两相渗流压裂水平井温度剖面预测［J］.天然气地球科学，2019，30（3）：389-399.

LUO H W， LI H T， LIU H B， et al. Prediction temperature profile of fractured horizontal well with two-phase flow in low-permeability gas reservoirs［J］.Natural Gas Geoscience， 2019， 30（3）： 389-399.

35
TIAN L， CHAI X L， WANG P， et al. Productivity prediction model for stimulated reservoir volume fracturing in tight glutenite reservoir considering fluid-solid coupling［J］.Frontiers in Energy Research， 2020， 8：573817.

36
郜益华，张迎春，杨宝泉，等.复杂断块油田跨断层水平井产能预测及分段长度优化方法——以西非A深水油田为例［J］.石油学报，2021，42（7）：948-961.

GAO Y H， ZHANG Y C， YANG B Q， et al. Productivity prediction and optimization method of segment length for cross-fault horizontal well in complex fault-block oilfield：A case study of the deepwater oilfield in West Africa［J］. Acta Petrolei Sinica，2021，42（7）：948-961.

37
WANG Z C，TIAN L，HUANG W K，et al. A model for evaluating relative gas permeability considering the dynamic occurrence of water in tight reservoirs［J］.Fuel，2025，386：134240.

38
胡勇，李熙喆，徐轩，等.含水致密砂岩气藏可动用储量评价新方法及其应用［J］.石油学报，2021，42（3）：332-340.

HU Y， LI X Z， XU X， et al. A new evalution method for recoverable reserves of water-bearing tight sandstone gas reservoirs and its application［J］. Acta Petrolei Sinica，2021，42（3）： 332-340.

39
胡勇，梅青燕，王继平，等.致密砂岩气藏井网加密优化［J］.天然气地球科学，2020，31（9）：1326-1333.

HU Y， MEI Q Y， WANG J P， et al. Optimization of well pattern infilling in tight sandstone gas reservoir［J］. Natural Gas Geoscience， 2020， 31（9）： 1326-1333.

40
张洪军，李新春，王瑞刚，等.压裂直井和水平井的探测区域计算公式［J］.断块油气田，2021，28（4）：535-540.

ZHANG H J， LI X C， WANG R G， et al. Investigation area calculations for fractured vertical well and horizontal well［J］. Fault-Block Oil & Gas Field， 2021， 28（4）： 535-540.

41
陈志明，廖新维，赵晓亮，等.低渗透致密气藏水平井探测半径研究［J］.特种油气藏，2015，22（5）：90-94，155.

CHEN Z M， LIAO X W， ZHAO X L， et al. Study on the detection radius of horizontal wells in low-permeability tight gas reservoirs［J］.Special Oil & Gas Reservoirs，2015，22（5）：90-94， 155.

42
郭智，位云生，孟德伟，等.苏里格致密砂岩气田水平井差异化部署新方法［J］.天然气工业， 2022，42（2）：100-109.

GUO Z，WEI Y S，MENG D W，et al. Differential deployment of horizontal wells in the Sulige tight sandstone Gasfield［J］. Natural Gas Industry， 2022， 42（2）：100-109.

43
雷群，胥云，才博，等.页岩油气水平井压裂技术进展与展望［J］.石油勘探与开发，2022，49（1）：166-172，182.

LEI Q，XU Y，CAI B，et al. Progress and prospects of horizontal well fracturing technology for shale oil and gas reservoirs［J］.Petroleum Exploration and Development，2022，49（1）：166-172，182.

Options
文章导航

/

〈 〉

陇ICP备2021001824号-7　 甘公网安备 62010202000678号
版权所有 © 《天然气地球科学》编辑部
地址：甘肃省兰州市天水中路8号　
邮编：730000　
电话：(0931)8277790　
E-mail：geogas@lzb.ac.cn
总访问量 　 今日访问 　 在线人数
技术支持：北京玛格泰克科技发展有限公司