0 引言
国内外主要页岩气盆地的储层初始含水饱和度介于10%~50%之间［5］。一般认为，储层初始含水饱和度由烃源岩生气充注不完全形成。由于页岩基质的孔渗低，岩心驱替实验结果表明页岩束缚水饱和度最高可达70%［6-7］。也即，页岩初始含水饱和度通常低于其束缚水饱和度，学者们解释该现象是由成藏过程中液态水的蒸发以及天然气对水蒸气的携带作用（汽化携液）造成［8-9］。因此，较多学者采用水蒸气吸附实验（又称为平衡水实验）来制作页岩的初始含水饱和度，并结合低温N2吸附实验评价含水在孔喉中的分布。此外，还有3种较为常见的研究方法：①水蒸气吸附实验，SANG等［10］利用不同湿度环境获取了Illinois盆地页岩的不同含水饱和度，进一步利用低温N2吸附实验评价了不同矿物孔隙中的含水分布特征；②分子模拟（MD），JIN等［11］采用分子模拟了甲烷—水在蒙脱石纳米孔中的竞争吸附特征；HU等［12］构建页岩干酪根分子模型，模拟了烃类分子与水分子在干酪根孔隙的分布特征；③基于规则形状孔隙假设的解析建模，LI等［5］分别假设狭缝孔和圆管孔，基于分离压理论建立了页岩不同尺度孔隙中的水膜厚度计算模型。尽管这些研究方法对页岩气水的认识有重要的推进作用，但这些研究方法分别具有缺乏直观性、研究尺度小和相对理想的局限性，不能有效区分实际页岩储层不同类型、不同尺度孔隙中的含水分布特征。
学者们近些年来逐渐意识到储层原始含水特征对页岩气赋存方式具有重要影响，认为基于干燥样品的吸附实验对页岩吸附气含量的评价结果可能会导致页岩气资源量被高估［13］。目前对于页岩储层含水对甲烷的吸附影响的研究主要有以下3种方法：①平衡水条件下的页岩气等温吸附实验，齐荣荣等［14］基于改进的容积法等温吸附实验装置，测量平衡水条件下页岩的甲烷等温吸附曲线；②分子模拟（MD），梁洪彬等［15］构建了海相页岩干酪根分子模型，揭示了高温高压条件下原生水对甲烷吸附的影响；③基于规则形状孔隙假设的解析建模，李靖等［16］提出了黏土孔隙壁面的水分子铺展系数，采用狭缝孔假设建立了不同水分子铺展系数下的甲烷吸附量计算方法。综上所述，与页岩含水分布相似，目前也需要寻求一种其他方法获取孔隙水分布条件下页岩三维孔隙空间的甲烷吸附可视化研究。
据此，本文研究采用一种介观的模拟方法——LBM模拟方法，分别建立页岩水蒸气吸附和甲烷吸附的LBM模型，可视化研究页岩三维孔隙网络中的含水分布及其对甲烷吸附的影响。在LBM框架下，引入粒子间作用力模型在LBM中考虑分子间作用力，同时耦合真实状态方程表征吸附过程的热力学行为；对建立的水蒸气吸附和甲烷吸附模型进行验证；构建包含有机质孔和无机孔的三维数字岩心，利用建立的LBM模型，分别开展干燥页岩和含水页岩的甲烷吸附研究，揭示气—液—固三相条件下甲烷吸附规律。本文研究相关成果可为页岩吸附气含量评价、页岩气藏数值模拟、页岩气储量分布预测等提供理论支撑。
1 数学模型
1.1 LBM基本框架
式中：f （x， t）和f （x，t）分别为分布函数和平衡分布函数；Δt为迭代时间步长；τ为松弛时间，与运动黏度υ e相关，可以表示为υ e/（c ×Δt）+0.5（声速c s = ）。本文采用D3Q19格子模型模拟三维空间的流体赋存，D3Q19模型中的格子离散速度ei 可以表示为［19］：
平衡分布函数定义为：
式中：wi 为不同速度方向的权重因子，取值为：
宏观的属性参数比如密度和速度可以由粒子分布函数确定：
,
1.2 粒子间作用力
式中：G ff为一个类似于温度的参数，可以调整流体之间的作用力。其值为负表示吸引力，其值为正则表示排斥力。可以通过对比Maxwell重构方法的结果，调节系数β来减少热动力不一致性。前文的标定结果表明，β=1.16时效果较好［23］。
在含水分布的模拟中，流体—壁面间作用力通过调整壁面格点的流体密度获取，作用力模型表示为［24］：
式中：s（x+ei ）为指示函数，0为流体格点、1为固体格点。值得注意的是“壁面密度”不是真正的固相密度，其仅用于调整不同的壁面性质。
在超临界甲烷吸附的模拟中，吸附往往发生在邻近壁面的1~2层，这里采用不同的流体—壁面间作用力。壁面伪势表示为第一个吸附层的伪势，通过调节作用力参数G fs表征为：
通过修正原始LBM框架的平衡速度u eq，可以将上述的作用力F total（F total = F ff + F fs）耦合至LBM体系中：
流体的压力可以通过泰勒展开得到，表示为：
1.3 状态方程
LBM能模拟热动力学行为的关键在于真实状态方程的引入。相对于理想状态方程，真实状态既能提高多相流体间的密度比，也能降低相界面处的虚假速度［25］。通过引入状态方程，流体的有效质量可以通过如下的形式表征：
值得注意的是，当引入真实状态方程后，温度直接由状态方程显性表示，不再与流体—流体间的作用力参数G ff相关，其在联合式（6） 和式（11） 时被消掉，这里仅起到保证根号内数值为正的作用。
在含水分布的模拟中，固体壁面的润湿性由壁面流体密度决定，这里将G ff和G fs都设置为-1/3，而甲烷吸附的模拟中，甲烷与壁面的作用力则由G ff和G fs的相对大小决定。这里采用Peng-Robinson （PR） 状态方程来描述气态水—液态水或游离态甲烷—吸附态甲烷的热动力学行为，可以表示为［26］：
式中：a=（0.457 235R2T 2 ）/p c，b=（0.077 796RT c）/p c，α（T）=（1+（0.374 64+1.542 26ω－0.269 92ω2 ）［1－（T/T c）0.5］2。对于不同流体的偏心因子ω取值不同，水取值为0.344，甲烷取值为0.11，其他的参数设置为a = 2/49，b = 2/21，R = 1，因此格子单位下甲烷的临界温度和临界密度分别为0.073和0.06。
2 模型验证
根据LDFT理论［31］，气体占据近壁面第一层吸附位的概率与固体壁面的侧向作用能（ε A）和表面作用能（ε 0）相关，侧向作用能（ε A）仅与吸附气体类型和温度相关，而表面作用能（ε 0）则与吸附气体类型和吸附材料相关。因此，可以通过LDFT理论计算理想材料下的甲烷吸附曲线，通过调节LBM的作用力参数G ff和G fs，论证LBM模拟与LDFT理论计算的一致性。
这里建立一个10 nm的狭缝孔隙，模拟50 °C条件下的吸附过程。模型的上下设置为固体壁面，固体壁面采用无滑移的弹性碰撞边界，左右两端采用Zou-He定压边界。在孔隙中设置密度为0.01的初始值（0.1 MPa），左右边界以每时间步10-4的密度增量增加，模拟气体注入增压吸附的过程（该密度增量较小，可以视为准静态过程），每1 000个时间步记录一次密度分布。为便于参数调节，下文的吸附模拟中G ff 始终设置为1。本文认为模拟中靠近壁面的第一层分子密度为吸附层密度，吸附曲线的模拟计算结果如图1（a）所示。可以发现，通过调节不同的固体壁面作用力G fs，可以模拟不同性质材料的吸附过程。当G fs = 1时，流体—流体作用力与流体-壁面作用力一致，不存在吸附。这里也展示了G fs = 2.1时的近壁面分子密度分布情况［图1（b）］，可以发现不同压力下LBM模拟的分子层密度与LDFT的计算结果也具有较高的吻合度。
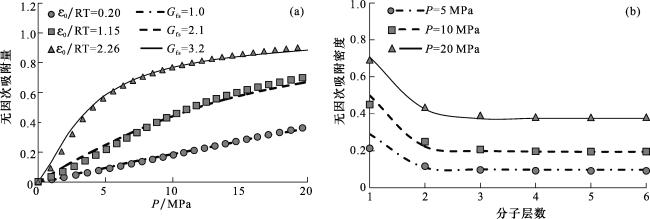
图1 不同流固作用力下LBM预测的甲烷吸附曲线与LDFT计算结果对比（a） 和不同压力下LBM预测（散点）的近壁面甲烷密度与LDFT计算（线）结果对比（b）Fig.1 （a） Comparison of the adsorption curves by LBM （under tuning fluid-solid force G fs） and LDFT theory （tuning ε 0 ）； （b） Comparison of the density distribution under different pressure by LBM （symbols） and LDFT theory （lines） |
这里进一步验证了LBM模型预测实际页岩超临界甲烷等温吸附的实验结果。2021年，胡科等［32］采用重量法吸附仪测试了四川盆地龙马溪组干燥页岩在不同温度下的过剩吸附曲线。由于其测试为页岩粉末（60~80目），无法获取孔径分布，这里LBM模拟仅用理想单个孔隙代替，重点评价LBM是否可以表征不同温度下的吸附密度（单位质量页岩的吸附体积）。理论上，可以通过建立G fs/G ff和ε 0/ε A的关系，实现对LBM中作用力参数（G fs和G ff）的调节。但由于实验页岩的非均质特征，实际页岩样品的作用能ε 0和ε A很难确定。因此，本文推荐直接调节G fs和G ff的方式拟合实验结果。根据Gibbs过剩吸附量的定义，吸附气密度与体相气密度差值与过剩吸附量成正比［32］，通过计算LBM模拟吸附气与体相气密度差值，拟合某温度下的实验曲线获取比例系数，可获取不同温度、压力下的过剩吸附量曲线，拟合结果如图2所示。由于模拟中将页岩粉末形成的多孔介质假设为单个孔隙，模拟结果有一定偏差，但总体而言，LBM可以拟合不同实验温度调节下的结果。因此，本文建立的超临界态甲烷吸附LBM模型是可靠的。
3 结果与讨论
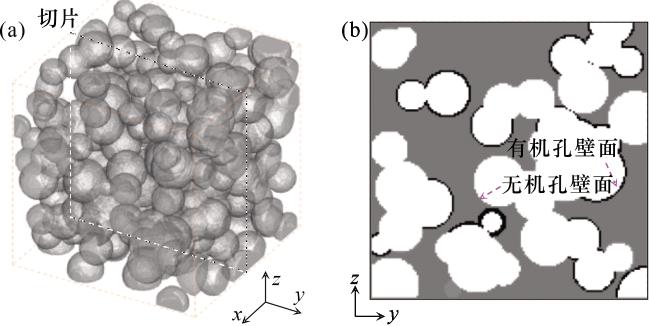
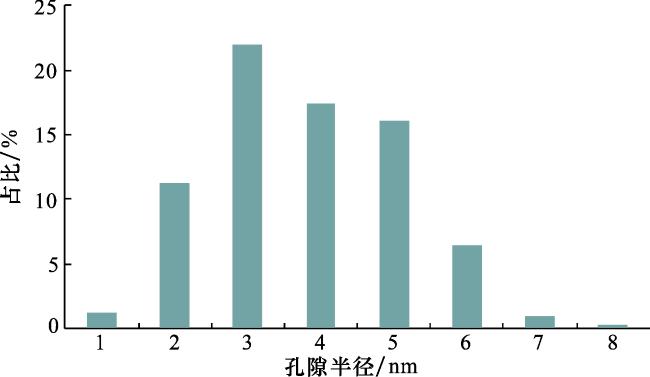
3.1 数字岩心重构
页岩基质的表征单元尺度一般大于100 μm×100 μm×100 μm，在目前的计算资源条件下，孔隙尺度的直接数值模拟方法无法在满足表征单元尺度的同时，也能捕捉纳米孔隙中的物理化学现象［33］。因此，本文采用随机算法建立一个简单的纳米多孔介质，旨在可视化表征页岩复杂孔隙网络中的气水分布特征及其对甲烷吸附的影响。
3.2 干燥页岩吸附特征
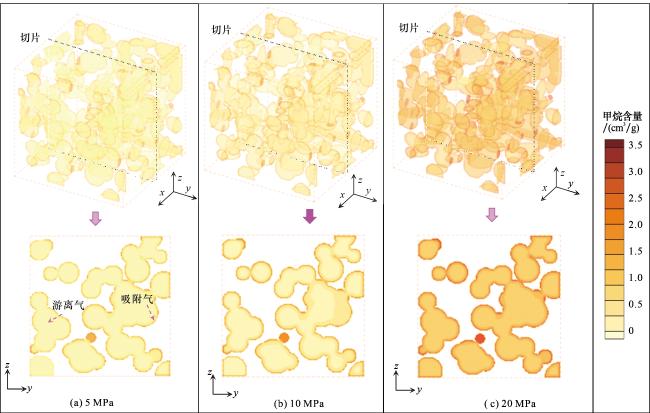
3.2.1 气体分布可视化
本文通过采用第3节实验拟合出的LBM作用力参数，开展基于图3所示数字岩心的气体分布可视化模拟。在本节的模拟中，仅考虑干燥页岩的模拟，不考虑页岩的初始含水分布。为保证物质守恒，将模型的y方向和z方向的4个外表面设置为封闭固体边界，固体壁面采用无滑移弹性边界，x方向的进出口采用压力边界，初始条件与压力边界条件的设置与第3节一致。
由于有机质孔与无机孔壁面性质差异，其对甲烷分子的作用力也有差异，但拟合实验中（图2）未予以区分有机质吸附与无机质的吸附，吸附的结果为两者的平均值。因此，在干燥页岩的LBM模拟中，也未对有机质孔和有机质孔壁面的作用力予以区分（后续研究可以通过拟合“区分了有机质和无机质的吸附曲线”开展模拟），模拟的结果如图5所示。可以发现，受到壁面作用力的影响，甲烷在壁面发生吸附，密度明显比体相游离气的密度高，游离气与吸附气的特征明显。在孔隙的角隅处，甲烷分子受周边固体壁面的作用更强，吸附的甲烷分子密度更高［30］。当压力增加后，体相气体被压缩、密度增加，同时，气体分子吸附在壁面的概率也增加，吸附气密度也相应增加。
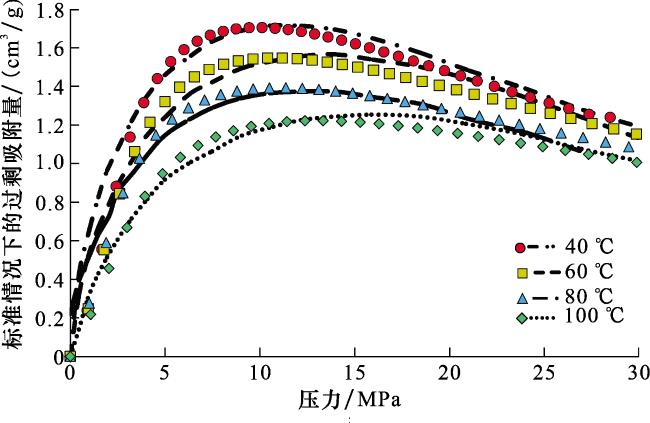
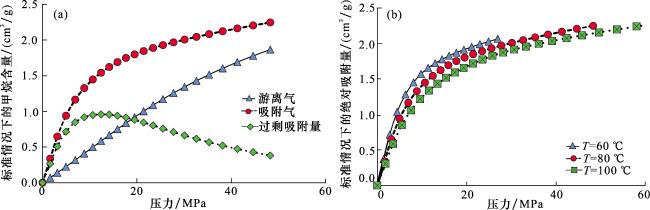
3.2.2 温压对吸附的影响
将所有靠近孔隙壁面第一层甲烷分子的平均密度认为是吸附气的密度，将孔隙中剩余甲烷分子的平均密度认为是游离气的密度，可以得到不同压力下游离气与吸附气的甲烷含量，而吸附气与游离气的密度之差则为过剩吸附量，如图6（a）所示。随着压力增加，游离气的密度在早期基本呈线性增加，后期密度的增加幅度则略微降低，与理论数据的变化一致；随着压力增加，吸附气的密度在早期快速增加（快速吸附），而在后期密度的增加则大大放缓，很好地表征了低压壁面吸附位多、吸附概率高，高压壁面吸附位少、吸附概率低的特征；随着压力增加，过剩吸附量呈现先增加后减少的特征，在12 MPa左右达到峰值。进一步地，模拟了不同温度下甲烷在多孔介质中的吸附特征，获取的吸附曲线如图6（b）所示。随着温度升高，甲烷的运动能量增加，孔隙壁面俘获甲烷分子概率降低，页岩对甲烷的吸附能力下降，与实验观察结果相符［36］，也从理论模拟的角度证实了，在相同的含气性条件下，深层页岩储层吸附气比例（相对于游离气）少于中浅层页岩的事实。
3.3 含水页岩吸附特征
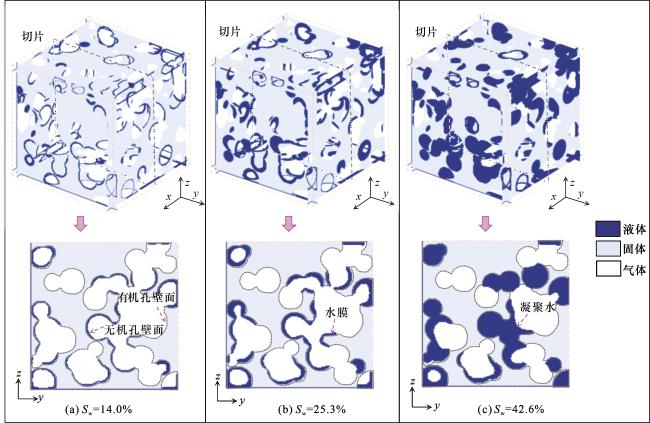
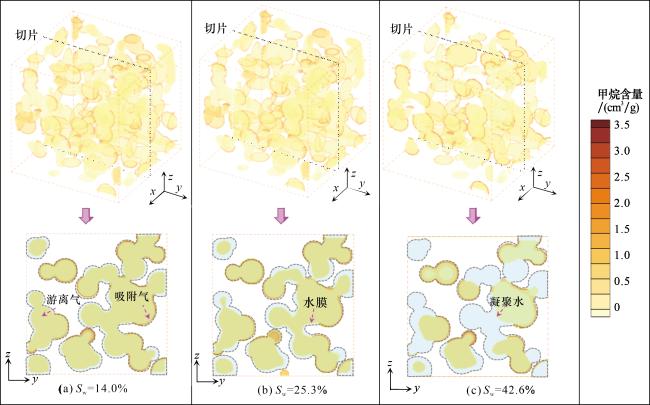
3.3.1 含水分布可视化
将上述LBM模型的温度设置为小于临界温度时（亚临界态），模拟空间中的流体将发生相分离，形成液相和气相，模拟束缚水的蒸发—吸附过程，形成页岩的初始含水分布［23］。这里采用前文标定好的参数（Tr = 0.85）开展模拟，模拟采用的数字岩心如图3所示，模型中将疏水有机质孔和亲水无机质孔的润湿角分别设置为120°和0°。这里需要说明的是，这种润湿性设置忽略了有机质孔隙内的极性官能团，即不考虑水分子吸附于极性官能团附近［12］；另外，假设研究区的有机质生烃能力足够强，原始有机孔内不含可动水［13］。同样，模型的y方向和z方向的4个外表面设置为封闭固体边界、采用无滑移弹性边界，x方向的进出口采用压力边界，孔隙空间初始密度值与压力边界的密度值大小一致。通过设置不同的初始密度值（0.07、0.09和0.12）和对应的压力边界条件，获取了不同的含水饱和度分布（14.0%、25.3%和42.6%），如图7所示。
对于无机质孔隙，受亲水吸引力的影响，水相在无机质孔隙发生吸附：在大孔隙处的含水量较低，水相主要以水膜的形式吸附在孔隙表面，而小孔隙对邻近水分子的作用力更强，水易在小孔隙发生凝聚、充填；对于有机质孔隙，受疏水排斥力的影响，水相无法在有机质孔壁面发生吸附、凝聚，壁面始终不含水。值得注意的是，实际页岩储层中，有机质孔壁面的极性官能团可能会吸附一些局部水分子，但整体而言有机质孔壁面不吸附水，这是因为，在甲烷—水蒸气的竞争吸附下，甲烷总是优先吸附于疏水有机孔壁面。
总体而言，无机质呈现“小孔隙充填水、大孔隙附着水膜”的特征，而有机质则始终不含水。当页岩初始含水饱和度较低时（如S w = 14.0%），孔隙中水分子主要以水膜的形式吸附在孔隙表面，仅有局部小孔隙中水是以液滴的形式充填；当初始含水饱和度较高时，液滴充填概率增加，水相以水簇的形式大量分布于各个孔隙中，使得大量孔隙由连通状态变为不连通状态，严重影响孔隙的有效连通性（如S w = 42.6%）。因此，不同含水饱和度下，孔喉配置关系和有机孔分布方式对有效流通路径的影响非常大，蒸发—吸附形成的气水分布特征与驱替形成的类似［37］。
3.3.2 含水对吸附的影响
对比图5可以发现，孔隙水的存在使得甲烷的吸附空间以及吸附特征产生明显变化。由于无机质孔隙壁面含水，甲烷无法吸附在其表面，仅能吸附在有机质孔隙壁面，吸附位的数量大大降低。一旦考虑储层含水，即便是在含水饱和度较少时（水相主要以水膜存在），无机质孔隙壁面也几乎无法吸附甲烷。因此，尽管黏土矿物的纳米孔隙发育，能够为甲烷吸附提供巨大的表面积，但在实际储层条件下，黏土矿物表面往往被水覆盖，对甲烷的吸附是无效的，在计算储量的时候，不应该考虑此部分的吸附气储量。当含水饱和度较低时，游离气仍可以占据较多的孔隙体积，但当含水饱和度较高时，游离气的赋存空间大大减小，导致甲烷的储量也会大大降低。值得注意的是，本文的模拟研究中仅能考虑水分子至少在无机质孔隙壁面铺展一层的情况，实际页岩储层中，受“汽化携液”现象的影响，当含水饱和度极低时，壁面水分子可能不完全铺展，能吸附一定的甲烷［16］。但是，总体而言，孔隙水饱和度的存在，使得甲烷的吸附位数量大大减少，在储量计算中需要予以重视。
通过对吸附态甲烷和游离态甲烷进行体积加权并求和，获得了不同含水饱和度下数字岩心中的甲烷含量曲线，如图9所示。可以发现，储层含水减少游离气的赋存空间和吸附气的吸附位，最终导致含水页岩比干燥页岩的储量少。当压力较低时，吸附气相对于游离气密度差异大，导致吸附气对储量贡献更大，若不考虑含水对甲烷吸附的影响，则储量计算的误差较大；当含水饱和度较高时，吸附气占比高、对储量贡献更大，若不考虑含水对甲烷吸附的影响，则储量计算的误差也会较大。现有储量计算方法通过采用含气饱和度考虑了储层含水对游离气的影响，但往往忽略含水对吸附气的影响［38］，若直接采用基于干燥页岩的吸附测试数据计算储量，储量的误差较大（本算例可达到30%）。特别是对于黏土含量较高的陆相页岩与海陆过渡相页岩［3］，其黏土在实验测试时供甲烷吸附的比表面积大，但在实际储层中该部分的吸附气不应被计入储量中。值得注意的是，不同温度下水相的赋存形态可能发生变化，但因为相变条件下格子单位与真实物理单位之间转换的问题，本文未考虑温度对含水环境下甲烷吸附的影响，未来有必要开展进一步研究。
4 结论
（1）建立了页岩甲烷吸附的LBM模拟方法，模型得到了理论与实验验证，验证内容包括：LDFT理论预测的甲烷等温吸附曲线、分子层密度分布和实验测试的龙马溪组页岩过剩吸附曲线。结合笔者最新建立的含水分布LBM模型，实现了可视化模拟页岩三维复杂孔隙空间中的含水分布及其对甲烷吸附的影响。
--引用第三方内容--
（2）在页岩孔隙的角隅处，甲烷分子受周边固体壁面的作用力更强，吸附的甲烷分子密度更高；随着压力增加，过剩吸附量呈现先增加后减少的特征，本文算例在12 MPa左右达到峰值；随着温度升高，页岩对甲烷的吸附能力下降，从理论模拟的角度证实了深层页岩吸附气含量少于中浅层页岩的事实。
（3）在页岩三维孔隙网络中，受亲水吸引力的影响，无机质呈现“小孔隙充填水、大孔隙附着水膜”的特征，而受疏水排斥力的影响，有机质始终不含水。含水饱和度较低时，水分子主要以水膜的形式吸附在孔隙表面，仅局部小孔隙水以液滴形式充填；含水饱和度较高时，水相以水簇的形式大量分布，使得大量连通孔隙变得不连通。不同含水饱和度下，孔喉配置关系和有机孔分布方式对有效流通路径的影响极大。
（4）原始储层无机质孔隙壁面含水，甲烷无法吸附在其表面，仅能吸附在有机质孔隙壁面，吸附位的数量大大降低。当压力较低和含水饱和度较高时，不考虑含水对甲烷吸附影响会导致计算的储量被高估（本算例可达到30%），特别是对于黏土含量较高的陆相/海陆过渡相页岩，需要考虑含水对甲烷吸附的影响。
甘公网安备 62010202000678号
