天然气地球科学 >

2024 , Vol. 35 >Issue 7: 1289 - 1303

DOI: https://doi.org/10.11764/j.issn.1672-1926.2023.12.002

天然气开发

致密砂岩气水两相流固耦合裂缝动态闭合分析半解析模型

  • 杜旭林 , 1, 2 ,
  • 苏彦春 , 1 ,
  • 房茂军 1 ,
  • 马明 3 ,
  • 白玉湖 1 ,
  • 程林松 2
展开
  • 1. 中海油研究总院有限责任公司非常规研究院，北京 100028
  • 2. 中国石油大学（北京）石油工程学院，北京 102249
  • 3. 宾夕法尼亚州立大学能源与矿业工程系，美国 宾夕法尼亚州 16802
苏彦春（1973-），男，河南西平人，硕士，教授级高级工程师，主要从事海洋与非常规油气开发管理和综合研究.E-mail：.

杜旭林（1992-），男，满族，河北保定人，博士，博士后，主要从事非常规油气渗流及数值模拟研究.E-mail：.

收稿日期: 2023-09-04

  修回日期: 2023-11-09

  网络出版日期: 2024-01-03

收起

A semi-analytical model coupled gas-water two-phase flow and geomechanics for dynamic closure analysis of fractures in tight sandstone

  • Xulin DU , 1, 2 ,
  • Yanchun SU , 1 ,
  • Maojun FANG 1 ,
  • Ming MA 3 ,
  • Yuhu BAI 1 ,
  • Linsong CHENG 2
Expand
  • 1. Unconventional Research Department，CNOOC Research Institute Co. ，Ltd. ，Beijing 100028，China
  • 2. College of Petroleum Engineering，China University of Petroleum （Beijing），Beijing 102249，China
  • 3. Department of Energy and Mineral Engineering，the Pennsylvania State University，Pennsylvania 16802，USA

Received date: 2023-09-04

  Revised date: 2023-11-09

  Online published: 2024-01-03

Supported by

The Key Research Subject for the 14th Five-Year Plan of CNOOC （Ltd.） Technology Project(KJGG2022-1004)

the Technology Project of CNOOC Research Institute(2022-ZYZL-FCG-04)

Fold

摘要

在致密砂岩气井压裂液返排和早期生产阶段，由于支撑剂回流和储层压降易于造成裂缝不同程度的闭合，从而导致产能的部分损失。为了分析这一关键问题，提出了用于预测压裂液返排和致密气藏早期开发产能的渗流—地质力学方程组完全耦合的半解析数学模型及求解方法，该方法可用于捕捉裂缝的动态行为并获取相关重要参数，以优化致密气开发策略。其中，结合致密气井普遍产水的矿场实际，建立了裂缝系统气水两相渗流方程组；根据裂缝表面不同受力关系，分别建立了人工裂缝与天然裂缝的力学方程，采用了裂缝开度与作用于裂缝壁面的接触应力间的非线性关系描述裂缝闭合；以迭代耦合方式求解渗流—地质力学耦合系统，采用了有限差分法对裂缝内流动求取数值解，获取裂缝的传导率初始分布，通过位移不连续法计算裂缝开度变化，并在渗流方程组中更新迭代以得到气水两相的流体压力与饱和度分布。将该模型与经典解析解及商业模拟软件的计算结果进行对比，验证了解的准确性。将其应用于鄂尔多斯盆地东缘某致密气田的实例井分析，研究表明：在返排及开发早期阶段，裂缝开度随着缝内压力降低而逐渐减小，在井筒射孔点、裂缝相交处、裂缝尖端更容易趋于闭合；由于裂缝成因不同，人工裂缝与天然裂缝有着不同的闭合机制，受支撑剂作用的影响，人工裂缝闭合程度要明显小于天然裂缝；通过拟合实测生产历史数据，能有效评估裂缝的关键参数。该研究对于综合利用早期生产数据准确预测气井产能及控压生产理念的提出具有重要的理论和现实意义。

关键词： 致密气藏; 返排; 气水两相; 渗流—地质力学耦合; 裂缝闭合; 位移不连续法; 半解析模型

本文引用格式

杜旭林 , 苏彦春 , 房茂军 , 马明 , 白玉湖 , 程林松 . 致密砂岩气水两相流固耦合裂缝动态闭合分析半解析模型[J]. 天然气地球科学, 2024 , 35(7) : 1289 -1303 . DOI: 10.11764/j.issn.1672-1926.2023.12.002

Abstract

During fracturing fluid flowback and the early production stage of tight sandstone gas wells， proppant flowback and reservoir pressure drop are possible to cause fracture closure to varying degrees， resulting in partial loss of productivity. To analyze this key problem， a fully coupled semi-analytical mathematical model and solution method of flow and geomechanical equations were proposed for predicting fracturing fluids flowback and early development productivity of tight gas reservoirs. This method can be used to capture the dynamic behavior of fractures and obtain relevant important parameters to optimize development strategies for tight gas reservoirs. Among them， the gas-water two-phase flow equations of fracture systems are established based on the field practice of water production in tight gas wells. According to the different stress relationships on the fracture surface， the mechanical equations of artificial and natural fractures are established respectively. The nonlinear relationship between the fracture aperture and the contact stress acting on the fracture wall is used to describe the fracture closure. The coupling system of flow and geomechanics is solved by the iterative coupling method. The finite difference method is used to obtain the numerical solution of the flow in fractures and obtain the initial distribution of fracture conductivity. The change of fracture aperture is solved by the displacement discontinuity method， and updating the iteration in the fluid flow equation group to obtain the pressure and saturation distribution of gas and water phases.The model results in this paper are compared with the classical analytical solutions and the commercial simulation software Abaqus to verify the accuracy of solutions. It is applied to the case analysis of tight gas fields in the eastern margin of Ordos Basin.The research result shows that： in the early stage of flowback and development， the fracture aperture gradually decreases with the decrease of the pressure inside the fracture， and tends to close more easily at the wellbore perforation point， fracture intersection， and fracture tip. Due to the different causes of fractures， artificial fractures and natural fractures have different closure mechanisms. Affected by the effect of proppant， the closure degree of artificial fractures is smaller than that of natural fractures.By fitting the measured production history data，the key parameters of fractures can be effectively evaluated.This study has important theoretical and practical significance for accurately predicting gas well productivity and proposing the concept of controlled-pressure production by comprehensively utilizing early production data.

Key words： Tight gas reservoirs; Flowback; Gas-water two-phase; Coupled flow and geomechanics; Fracture closure; DDM; Semi-analytical model

0 引言

水力压裂是一种通过高压将大液量压裂液和支撑剂材料注入以打开地层的技术，目前已成功应用于非常规油气资源的高效开发，使得致密砂岩气的大规模商业性开采成为可能［1-3］。在致密气开采过程中，大部分压裂井表现出了产量递减迅速，油压稳定下降的生产特征，且大量试井解释和产量递减分析结果得到的人工裂缝长度要普遍小于压裂工艺设计长度。根据现有文献［4-5］报道，这种生产特征被认为是由于衰竭开发产生的压力降和支撑剂颗粒回流两方面因素所引起的裂缝部分闭合导致的。现阶段经过现场试验表明，通过精细化控制井下压力，能减缓气井产量递减，增加最终可采储量。但是，这种控压生产理念尚且缺乏可靠的理论依据，也缺乏对裂缝动态闭合规律的有效认识。
关于压裂井返排及生产动态预测的研究方法包括：解析法、半解析法和数值解法。其中，解析法在现代产量递减分析中的应用最为广泛。ABBASI等［6］提出了压裂液返排和动态分析的经典解析模型，将生产动态划分为3个阶段，其中第一阶段以压裂液产出（单相水）为主，根据流量规整化压力（RNP）与物质平衡时间（MBT）之间的线性关系提取裂缝参数，但该模型无法捕捉突破后的压裂液返排特征，因为此时裂缝内为多相流，且由于缺乏地层流体的供给，裂缝内的压力迅速下降，导致裂缝开度及传导率急剧减小；SUN等［7］采用线性流的分区模型表征部分闭合的动态裂缝，并以样板曲线拟合和历史拟合的手段识别裂缝闭合的“夹点”；虞绍永［8］基于早期返排历史数据，结合物质平衡法求解了裂缝有效孔隙体积的解析解；严谨等［9］推导了考虑裂缝部分闭合和流量不均匀分布的压裂井不稳定产量解，绘制了相应的产量递减图版。总体而言，解析解的描述多以单相流体为主，且对于裂缝的刻画过于粗糙。
定量分析压裂液返排特征最为详尽的是数值解法。CLARKSON等［10］、WILLIAMS-KOVACS等［11］建立了压裂液返排的多相流数值模拟模型，每个压裂段考虑离散的双翼缝，详细描述了支撑剂回流过程中形成的一系列流态，并应用蒙特卡洛模拟方法评估拟合生产数据的裂缝参数的合理分布；KANFAR等［12］建立了三孔模型以表征具有水力裂缝、次生/天然裂缝、基质的复杂系统，考虑了流体重力分异和动态渗透率，描述了返排及长期开发过程中的生产动态；陈希［13］建立了压裂水平井气水两相压裂液返排的双孔双渗模型，分析了压裂参数、气体运移、毛管力、关井时间等对压裂液返排及产能的影响。然而，由于建立精细的数值模拟模型需要花费很长时间，且要处理较为庞大的计算量，因此数值解在应用层面同样存在一定限制。
半解析半数值法（简称为半解析模型）［14-17］结合了解析法与数值解法两者的优点，既保留了解析解的高精度，又如数值解法能处理较为复杂缝网形态下的非线性渗流方程。目前研究表明在压裂液返排阶段，裂缝的弹性变形是压裂液返排的主要驱动力，JIA等［18-19］针对致密油藏返排及早期开发阶段，根据裂缝壁面的受力关系进行流固耦合建模，指出随着裂缝内流体压力迅速下降，原本被压裂液充填的裂缝随着流体被采出，裂缝开度减小且部分裂缝段闭合，最终表现为裂缝真实导流能力迅速降低。此外，裂缝闭合会使得部分充满压裂液的水力压裂缝与次生诱导裂缝失去连接，导致返排和闷井过程中的压裂液滤失［20-22］，从而堵塞气相渗流通道，而利用流固耦合模型可有效分析裂缝闭合对压裂液返排率的影响。上述前人对于致密油藏压裂返排动态分析的探索，也为致密气藏研究工作带来了启发，但仍亟待解决的主要问题包括：其一，前人模型以单相或油水两相为主，与致密气的渗流特征不符；其二，尚未区分人工裂缝和天然裂缝的不同闭合机制，以相似的数学表达式对2类不同裂缝进行解释是不够严谨的；其三，忽视了闭合裂缝微小形变产生的应力变化，这在全耦合迭代过程中会造成一定的误差。
为此，本文根据鄂尔多斯盆地东缘致密气藏砂体普遍含水、采用多井型压裂衰竭开发的特点，建立了适用压裂气井返排及早期开发阶段生产动态分析的渗流—地质力学耦合迭代求解的半解析模型，该模型综合考虑了人工裂缝和天然裂缝不同的闭合机制，能定量捕捉裂缝形变的具体特征，获取有效的动态裂缝参数。本文成果有利于深化认识致密气藏开发动态特征，为精细化控压生产提供必备的理论依据。

1 物理模型及假设条件

致密砂岩储层中的裂缝分布包括水力压裂产生的人工裂缝和被开启的天然裂缝。以水平井为例，不同类型裂缝分布特征如图1（a）所示。在致密气开发过程中，随着砂体内部天然气的采出和气藏压力的下降，人工裂缝和天然裂缝呈现出不同的闭合状态，这与裂缝的成因密切相关。人工裂缝以张性裂缝为主，由于支撑剂充填的影响，在力学不平衡作用下，裂缝从开启逐渐闭合至支撑剂颗粒的粗糙表面上，具有一定的高导流能力，见图1（b）；天然裂缝常为剪切裂缝，在地应力作用下裂缝两侧分离的壁面逐渐接触，但由于裂缝天然的强非均质性，不会完全闭合，见图1（c）。
图1 致密气藏不同裂缝分布及开发过程中的闭合状态

Fig.1 Diagram of different fracture distribution and closure status during development of tight gas reservoirs

本文研究的是压后模拟，即水力压裂后压裂液返排及早期开发阶段。采用双孔双渗模型表征，即储层包括裂缝和基质两部分。其中，将预置裂缝离散化并分段排序，各裂缝网格长度可不一致，假设裂缝贯穿整个地层，裂缝高度等于地层厚度，将复杂问题转化为二维平面问题，基质不作离散。在压裂液返排过程中，假设原始状态裂缝内充满单相水（仅为压裂液），气体突破后裂缝内为气水两相，基质内的流动考虑为单相气，如图2（a）所示。对裂缝壁面进行受力分析，对于开启的裂缝，裂缝壁面处受到地应力和裂缝流体压力作用；对于闭合中的裂缝，人工裂缝与天然裂缝应予以区分，人工裂缝考虑存在支撑剂的影响，裂缝壁面处受地应力、流体压力和支撑剂的支撑力共同作用，如图2（b）所示，而天然裂缝无支撑力作用。
图2 基质—裂缝气水流动状态及受力分析

Fig.2 Diagram of gas-water flow and stress analysis in matrix and fracture

2 数学模型的建立

2.1　渗流方程组

基质内的流动可考虑为瞬态线性流［23］，其渗流方程见附录A。裂缝内则为气水两相一维流动，相应的非稳态渗流质量守恒方程为：
气相：
∂ ∂ x k F l k r g S F g μ g B g ∂ p F g ∂ x + q ˜ S C F g + q ˜ S C W g = 1 ∂ t ϕ F S F g B g
水相：
∂ ∂ x k F l k r w S F g μ w B w ∂ p F g - p c g w S F g ∂ x + q ˜ S C W w = 1 ∂ t ϕ F 1 - S F g B w
式中： q ˜ SCFg为由基质向裂缝供给的气体体积流量，d-1； q ˜ SCWg、 q ˜ SCWw分别为气相和水相的单位体积产量，d-1；t为时间，d；k F l 为裂缝渗透率（下标l取1，表示人工裂缝；取2，表示天然裂缝），μm2；k rg、k rw分别为气相、水相相对渗透率，无因次；p Fg为裂缝内的气相压力，MPa；p cgw为毛管力，MPa；μ g、μ w分别为气相和水相黏度，mPa·s；B g、B w分别为气相和水相体积系数，m3/m3；S Fg为裂缝内的气相饱和度，无因次；φ F为裂缝孔隙度，无因次。
人工裂缝渗透率采用BARREE模型［24］进行计算，认为人工裂缝渗透率是关于有效闭合应力与支撑剂材料属性的复杂函数，如下式：
k F 1 = 0.1 + K 0 - 0.1 1 + 145 σ n ' s 1 - m 2 L n d p 2 2
K 0 = k 1 d P m 1
式中： K 0为实验中岩样未受压时的裂缝绝对渗透率，μm2；σ׳n 为有效正应力，MPa；d p为支撑剂颗粒的中值直径，μm；式（3）和式（4）中的回归系数k 1、m 1、m 2、s 1与实验基础数据有关，取值可参考文献［5，24］，BARREE实验所用的支撑剂种类包括石英砂和高密度陶粒，石英砂按石英含量可细分为白砂和棕砂。
假设天然裂缝两侧壁面平行，其渗透率符合立方定律［25］：
k F 2 = w F 2 12
式中： w F为天然裂缝开度，m。

2.2　地质力学方程组

根据弹性力学平面应变假设，裂缝壁面处的应变包括正应变和剪切应变。这里针对不同裂缝的开启、闭合2种不同状态分别进行讨论。

2.2.1 闭合裂缝

由库伦准则［18-19］可知闭合裂缝壁面所受的剪切应力必须小于或者等于引起裂缝壁面滑移的摩擦阻力，为此引入额外项vη来描述高速滑移下的惯性，则含有阻尼项的库伦准则可表示为：
τ - ν η = μ F σ n ' + S 0
式中： τ为剪切应力，MPa；v为滑移速度，m/s；μ F为摩擦阻力系数，无因次；S 0为内聚力，MPa；其中： η为阻尼系数，表示为：
η = G 2 ν s
式中： G为剪切模量，MPa；v s为剪切波动速度，m/s。
以压应力为正，根据闭合裂缝壁面处的受力关系，有：
σ n ' = σ n - p F g - p p r o p
式中： σ n为正应力，MPa；p prop为支撑剂的支撑力，MPa。若分析对象为天然裂缝，p prop的大小等于0；若分析对象为水力裂缝，p prop的大小等于支撑剂颗粒的平均接触压力在裂缝壁面处的叠加［4］。
人工裂缝的闭合开度反映裂缝的真实导流能力，可采用修正的BARREE模型［5］进行计算，表达式右侧的第一项为裂缝内支撑剂充填的初始高度，受支撑剂浓度控制；第二项为人工裂缝孔隙结构压实导致的开度降低，受地应力和支撑剂粒径大小控制；第三项为支撑剂颗粒嵌入地层导致的支撑剂充填体高度的降低，受地层强度控制。
w F ' = 2.04 C p w 1 - 7.51 C p m 3 σ n ' d p m 4 - 2 d e ¯
式中： w F '为人工裂缝开度，m； C p为支撑剂浓度，g/cm2；表达式中的回归系数w 1、m 3、m 4同样源于BARREE实验［5，24］；d e为支撑剂颗粒嵌入地层的平均距离，m。
天然裂缝的闭合开度可由有效正应力与累积剪切滑移的实验关系式［26-27］计算得到：
w F = w 0 1 + 9 σ n ' σ n , R e f + D E f f t a n φ D i l 1 + 9 σ n ' σ n , R e f
式中： w 0是有效法向应力为0时的裂缝开度，m；σn ，Ref为接触参考压力，表示水力开度减小90%时测得的有效应力，MPa；φ Dil为裂缝开度的剪胀角，º；这三者为给定的常量，数值大小由实验室测得。D Eff为有效剪切位移，m；当D≤D Eff，max时，D Eff＝D，否则D Eff＝D Eff，max。其中，D为剪切位移，m；D Eff，max为最大有效剪切位移，m。

2.2.2 开启裂缝

当裂缝开启时，人工裂缝内的支撑剂颗粒在初始时刻处于悬浮状态，人工裂缝与天然裂缝均满足应力平衡条件，即裂缝壁面的有效正应力为0，同时由于裂缝内的流体不能承受剪切应力，因此裂缝壁面也不受剪切应力作用，对应的力学平衡方程为：
σ n = p F g
τ = 0
将接触应力为0时的裂缝开度w 0和裂缝孔径初值W 0作为临界值，在每次迭代求解后，对得到的各个裂缝单元的开度大小与临界值进行比较，以判断裂缝单元的开启或闭合状态。为保证裂缝在闭合前后开度大小的连续性，裂缝处于开启状态下的开度［28］可表示为：
W F = W 0 + E O p e n
w F = w 0 + D E f f t a n φ D i l + E O p e n
式中： W F为裂缝孔径（裂缝单位表面积所存储的流体体积），m。W F与w F在裂缝处于初始开启状态时候的大小是相等的，随着裂缝闭合发生不同程度的下降。E Open为裂缝壁面张开的距离，m。E Open的大小与计算得到的正位移不连续增量ΔE有关。

3 流固耦合迭代求解

3.1 求解地质力学方程

本文采用位移不连续法（DDM）计算每个时间步内的裂缝尺寸，以更新对应渗流方程中的流动空间及传导率。SHOU等［29］提出了无限大地层、二维、均质、各向同性、线弹性变形介质下微小形变的平面应变问题的经典DDM解法。该方法可求解在某个裂缝网格i内由于第j个裂缝网格发生的剪切应变ΔD和正应变ΔE而导致的相应的正应力和剪切应力变化Δσ、Δτ。根据叠加原理，可获得各个网格之间应力与应变的关系。
Δ σ n , i n + 1 = ∑ j = 1 n B E , σ i j G A d j , i j n + 1 E j n + 1 + ∑ j = 1 n B D , σ i j G A d j , i j n + 1 D j n + 1
Δ τ i n + 1 = ∑ j = 1 n B E , τ i j G A d j , i j n + 1 E j n + 1 + ∑ j = 1 n B D , τ i j G A d j , i j n + 1 D j n + 1
式中： Δσn，i n +1、Δτi n +1分别表示第n+1个时间步裂缝单元i变形引起的法向应力和剪切应力增量，MPa； E j n +1、 D j n +1分别为第n+1个时间步裂缝单元j的法向位移和剪切位移，m； G A d j , i j n + 1为修正系数［29］，无因次； B E ， σ 、 B D ， σ 、 B E ， τ 、 B D ， τ 均为DDM计算的相互作用系数矩阵［29］。
考虑闭合裂缝的微小形变产生的应力变化，将剪切应力表达式（6）、式（12）代入式（16），其中滑移速度v等于单位时间内的剪切位移量ΔD，得到以下关系。
开启裂缝：
τ i n + ∑ j = 1 n B E , τ i j + ∑ j = 1 n B D , τ i j Δ D j - Δ D i η = S 0 , O p e n
闭合裂缝：
τ i n + ∑ j = 1 n B E , τ i j Δ E j + ∑ j = 1 n B D , τ i j Δ D j - Δ D i η = μ F σ n ' + S 0
联立正应力表达式（8）、式（9）、式（10）、式（11）和式（15），得到以下关系。
开启裂缝：
σ n , i n + ∑ j = 1 n B E , σ i j Δ E j + ∑ j = 1 n B D , σ i j Δ D j = p F i
闭合裂缝：
E i n + Δ E i =                                                                                                                                                                                               
2.04 C p w 1 - 7.51 C p m 3 σ n , i n + ∑ j = 1 n B E , σ i j Δ E j + ∑ j = 1 n B D , σ i j Δ D j - p F i d p m 4 - 2 d e ¯ 人工 裂缝 E 0 1 + 9 σ n , i n + ∑ j = 1 n B E , σ i j Δ E j + ∑ j = 1 n B D , σ i j Δ D j - p F i σ n , R e f + D E f f t a n φ D i l 1 + 9 σ n , i n + ∑ j = 1 n B E , σ i j Δ E j + ∑ j = 1 n B D , σ i j Δ D j - p F i σ n , R e f 天然 裂缝
式中： σn，i n 为第n个时间步裂缝单元i变形引起的法向应力，MPa；p F i 为裂缝单元i的孔隙流体压力，MPa；Ei n 为第n个时间步裂缝单元i的法向位移，m；E 0为裂缝的初始法向位移，m；ΔEi 和ΔEj 分别为裂缝单元i和j的法向位移变化量，m；ΔDj 为裂缝单元j的剪切位移变化量，m。则联立式（17）、式（18）、式（19）及式（20），对应N个裂缝网格有2N个式子，每个网格具有ΔEi 和ΔDi 2个未知数，共2N个未知数，可求得各网格的ΔEi 和ΔDi，相应地计算出当前时间步的剪切位移不连续量D和正位移不连续量E。

3.2 求解渗流方程组

考虑到裂缝的弹性形变，即裂缝开度及传导率的动态变化，对式（1）和式（2）方程两侧同乘相应的体积项Vi，方程左侧乘以流体体积Vai，方程右侧乘以裂缝孔隙体积Vbi。
V a i = 2 a i h w F
V b i = 2 a i h W F
式中： h为缝高，m；ai 为对应裂缝网格i的中点到边界的距离，m。
获取裂缝内气相和水相流动方程在空间点和时间点（i，n+1）的有限差分离散格式如下：
气相：
∑ j = 1 ψ i T g i , j n + 1 p F g j n + 1 - p F g i n + 1 + q S C F g i n + 1 + q S C W g i n + 1 = α g 1 n + 1 E B g i n + 1 - E B g i n + α g 2 n + 1 S F g i n + 1 - S F g i n
水相：
∑ j = 1 ψ i T w i , j n + 1 p F g j n + 1 - p F g i n + 1 - P c g w i , j ' S F g i n + 1 - S F g i n + q S C W w i n + 1 = α w 1 n + 1 E B w i n + 1 - E B w i n + α w 2 n + 1 S F g i n + 1 - S F g i n
式中： ψi 为与裂缝单元i相邻的网格集合；T g i，j n+ 1、T w i，j n+ 1分别为第n+1个时间步裂缝网格i和j之间的气相和水相传导率，μm2·m； p F g i n + 1、 p F g j n + 1分别为第n+1个时间步裂缝网格i和j的气相压力，MPa； P c g w i , j '为裂缝网格i和j的毛管力，MPa； q S C F g i n + 1为第n+1个时间步第i个裂缝网格的气相传质量，m3； q S C W g i n + 1和 q S C W w i n + 1分别为第n+1个时间步井筒与第i个裂缝网格之间的气相、水相传质量，m3； α g 1 n + 1、 α w 1 n + 1分别为压力定义的气相和水相压缩系数，MPa-1； α g 2 n + 1、 α w 2 n + 1分别为饱和度定义的气相和水相压缩系数，MPa-1。其中，T、α和 P c g w i , j '的表达式见附录B。
考虑恒定流量井筒边界条件，恒定流量等于与井筒相连的各网格的源汇项之和：
q g , T o t a l = ∑ k q S C W g k
q w , T o t a l = ∑ k q S C W w k
式中：下角标k为与井筒相连的裂缝网格编号； q g , T o t a l、 q w , T o t a l分别为井筒产气量和产水量，m3； q S C W g k、 q S C W w k分别为与井筒相邻的裂缝网格k的气相和水相流量，m3。
各裂缝网格与井筒之间的传质量可由下式求得：
q S C W g k = - T g k , W n + 1 p F g k n + 1 - p W n + 1
q S C W w k = - T w k , W n + 1 p F g k n + 1 - p c g w k n + 1 - p W n + 1
式中： T g k , W n + 1、 T w k , W n + 1分别为第n+1个时间步与井筒相邻的裂缝网格k的气相和水相传导率，μm2·m； p F g k n + 1为第n+1个时间步裂缝网格k的气相压力，MPa； p c g w k n + 1为第n+1个时间步裂缝网格k的毛管力，MPa； p W n + 1为第n+1个时间步的井底流压，MPa。
裂缝网格与井筒网格之间的几何传导系数为：
G k , W = 2 h w k 3 12 a k
式中： wk 为裂缝单元k对应的开度，m；ak 为裂缝网格k的中点到边界的距离，m。
则裂缝网格与井筒网格之间的传导率为：
T g k , W n + 1 = G k , W k r g k , W n + 1 1 μ g B g k , W n + 1
由此，式（23）、式（24）可改写为式（31）、式（32）：
气相：
∑ j ∈ ψ i T g i , j n + 1 p F g j n + 1 + ( S F g ) j n + 1 - ∑ j ∈ ψ i T g i , j n + 1 p F g i n + 1 + T g k , W n + 1 p F g k n + 1 + α g 2 n + 1 ( S F g ) i n + 1 = - q S C F g i n + 1 - T g k , W n + 1 p W n + 1 + α g 1 n + 1 E B g i n + 1 - E B g i n - α g 2 n + 1 ( S F g ) i n
水相：
∑ j ∈ ψ i T w i , j n + 1 p F g j n + 1 - T w i , j n + 1 P c g w i , j ' ( S F g ) j n + 1 - ∑ j ∈ ψ i T w i , j n + 1 p F g i n + 1 + T w k , W n + 1 p F g k n + 1 - ∑ j ∈ ψ i T w i , j n + 1 P c g w i , j ' - α w 2 n + 1 ( S F g ) i n + 1 = - T w k , W n + 1 p W n + 1 + α w 1 n + 1 E B w i n + 1 - E B w i n - α w 2 n + 1 ( S F g ) i n
已知当前时刻的剪切位移不连续量Di n +1、正位移不连续量Ei n +1、裂缝内气相压力p Fg及含气饱和度S Fg可同时求解。基质渗流方程的离散格式见附录A。上述3N个方程对应3N个未知量，可求得当前时刻各个网格的气相压力p Fg及含气饱和度S Fg。

3.3 劈分迭代求解

在上述数学模型中待求的未知量包括当前时刻各裂缝网格的正位移不连续量E、剪切位移不连续量D、裂缝内的气相压力p Fg及含气饱和度S Fg。本文为保证良好的收敛性、最大程度地降低计算耗时，没有选择全耦合同步求解，而是采用了劈分迭代的耦合求解格式［30］，即在已知气相压力p Fg、含气饱和度S Fg情况下求解应力方程，得到相应的应变E和D；之后在应变E和D已知情况下求解气相压力p Fg、含气饱和度S Fg；再反算应变E和D，最终直至收敛。流固耦合迭代求解流程见图3。
图3 流固耦合迭代求解流程

Fig.3 Chart of flow-geomechanics coupled split-iterative solution

4 模型验证

4.1　力学模块的验证

SNEDDON等［31］提出了单条裂缝在恒定载荷作用下法向位移不连续性分布的经典解析解，通过对比求解恒定半缝长和裂缝内孔隙流体压力条件下的裂缝尺寸，验证本文模型力学模块的计算精度。其中，剪切模量为6 GPa，泊松比为0.25，最小水平主应力为30 MPa，裂缝半长为16.8 m，裂缝内流体压力与最小水平主应力的差值为1 MPa。本文模型采用了Lagrange插值的二阶精度DDM算法，需对裂缝进行离散化处理，分析了不同裂缝网格数目（N F＝11，44）对计算结果的影响，如图4所示。从图中可以看出，本文模型力学模块在不同裂缝网格数目条件下求解的裂缝开度分布与SNEDDON模型结果趋势完全一致，且随着裂缝离散单元数量的增加，可有效减弱单元间的“台阶效应”，本文模型结果与解析解之间的一致性增强，当裂缝单元数量达到44时，从裂缝中心部位到尖端的数据点的误差小于5%，说明了当裂缝网格数目达到足够多，本文模型的力学模块能够保证合理的准确性。此外，从模型适应性角度对比，解析解虽然精确，但通常局限于规则的理想情形，对于复杂情形往往找不到合适的解析解，而本文模型通过对裂缝系统离散化处理，能够适用于多缝及复杂缝网等多种情形，相比解析解具有更好的适应性。
图4 本文模型与SNEDDON解析解的裂缝开度计算结果对比

Fig.4 Comparison of fracture aperture calculated by the proposed model and SNEDDON’s solution

4.2　渗流模块的验证

将本文模型气水渗流模块与商业模拟软件tNavigator在预测压裂井返排及早期开发生产动态方面进行对比。图5为tNavigator所采用的全数值网格平面系统（2 m×2 m），其中对裂缝周围进行网格细化加密处理（网格大小为0.005~1 m），图中人工裂缝（红色）缝长为54 m，天然裂缝（蓝色）缝长为38 m，缝宽为0.005 m，在本算例中不考虑裂缝的形变。气层厚度为5 m，天然气相对密度为0.57。储层原始压力为15 MPa，压裂直井以恒定井底流压10 MPa控压生产。原始状态下，裂缝内饱和压裂液（S Fw=100%），基质内部含水饱和度为0.4。图6展示了tNavigator全数值模型与本文模型的模拟结果，返排初期以人工裂缝排水为主，此时基质作为气源向裂缝系统内部供气，表现为产气量的快速上升阶段，产水以注入流体为主；当压裂液返排结束时，产气量达到顶峰，气井正式进入开发阶段，随着地层压力的降低，产气量稳定下降，产水以地层水为主。
图5 tNavigator全数值模型中采用的全局网格系统

Fig.5 The global grid system used in the fully-numerical model by tNavigator

图6 本文模型与tNavigator的生产剖面计算结果对比

Fig.6 Comparison of production profile calculated by the proposed model and tNavigator

本文模型与tNavigator在气水生产剖面预测上展现了良好的一致性，表明了本文模型的渗流模块是合理且准确的。

4.3　耦合模块的验证

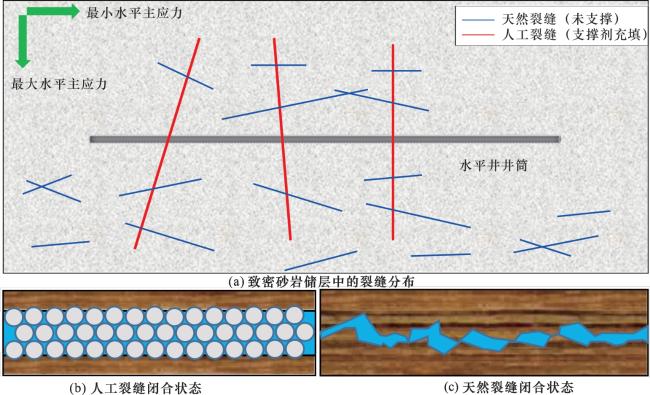
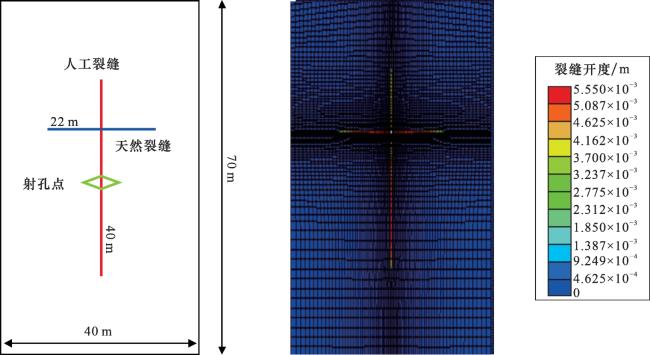
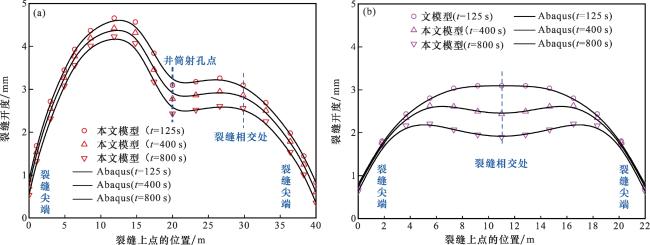
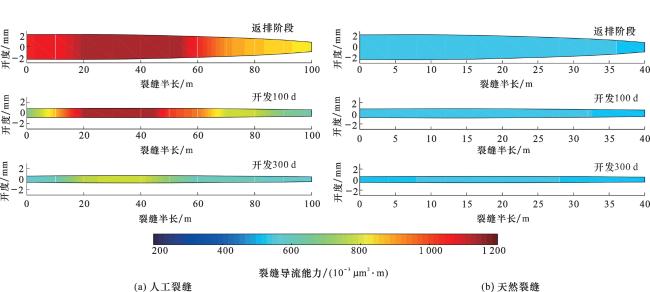
将本文提出的流固耦合模型与商业模拟软件Abaqus®SIMULIA有限元模拟器在预测返排及生产阶段的裂缝动态行为变化方面进行对比。该算例采用Abaqus®SIMULIA的Cohesive单元法建立的二维水力压裂模型，物理模型为直井压开一条人工裂缝，其中一侧遭遇一条天然裂缝，如图7（a）所示。水力压裂结束时刻的初始裂缝形态及开度分布如图7（b）所示，全局网格系统为非等间距网格，在裂缝处采用了过渡网格（网格尺寸为0.005~1 m）进行加密处理。以Abaqus®SIMULIA模拟的压后裂缝形态作为本文模型的初始条件，模型输入参数如表1所示。通过模拟压裂井早期开采阶段，对比两者在相同配产条件下所获取的关键参数。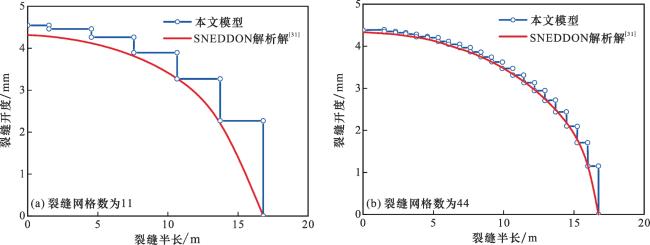裂缝接触的有效应力和裂缝渗透率之间的关系见表2，表明了随着气体被采出，地层流体压力逐渐降低，有效应力随之增大，人工裂缝与天然裂缝发生闭合，渗透率出现不同程度的下降；绘制了在气井开采125 s、400 s和800 s时刻人工裂缝和天然裂缝的开度分布情况分别如图8（a）、图8（b）所示，可以看出在井筒射孔点及裂缝相交处等压降较大的位置、裂缝尖端即水力压裂压力波及能量不足的位置，裂缝更易趋于闭合。本文模型对裂缝开度的解与Abaqus®SIMULIA结果对比，两者展现出较好的一致性，因此本文提出的流固耦合模型能够有效地捕捉气井合理配产下的裂缝真实几何形态，从而准确预测裂缝导流能力变化。
图7 Abaqus®SIMULIA模拟水力压裂结束时刻的初始裂缝形态

Fig.7 Initial fracture state at the end of the fracturing treatment simulated by Abaqus®SIMULIA

表1 模型输入参数

Table 1 Model input parameters

物理量 参数值 物理量 参数值
气藏厚度/m 10 基质渗透率/（10-3 μm2） 0.1
剪切模量/GPa 15 泊松比/无因次 0.1
最小水平主应力/MPa 30 水平主应力差/MPa 5
裂缝接触参考压力/MPa 29 裂缝初始开度/m 0.005
裂缝剪胀角/（º） 2.5 最大有效剪切位移/m 0.002
内聚力/MPa 2 摩擦阻力系数/无因次 0.6
原始人工裂缝半长/m 20 原始人工裂缝渗透率/（10-3 μm2） 3 000
原始天然裂缝半长/m 11 原始天然裂缝渗透率/（10-3 μm2） 500
表2 有效应力与不同裂缝渗透率间的关系

Table 2 The relationship between fracture permeability and effective stress

有效应力/MPa 0 5 10 20 30
人工裂缝渗透率/（10-3 μm2） 3 000 2 697.3 2 394.5 1 789.1 1 183.6
天然裂缝渗透率/（10-3 μm2） 500 348.8 237.1 133.3 96.4
图8 本文模型与Abaqus®SIMULIA的裂缝开度计算结果对比

(a)人工裂缝开度分布；(b)天然裂缝开度分布

Fig.8 Comparison of fracture aperture calculated by the proposed model and Abaqus®SIMULIA

从计算效率来看，Abaqus® SIMULIA为全数值模型，需要对基质和裂缝同样剖分网格，而本文模型为半解析模型，仅对裂缝系统剖分网格，网格数量远远少于全数值模型，整个计算过程耗时为516.5 s，约是Abaqus®SIMULIA总耗时的1/3，因此本文模型相比此类数值模拟软件具有明显的速度优势。

5 实例分析

将本文提出的流固耦合模型应用于鄂尔多斯盆地东缘致密气藏的实际开发中。某孤立型砂体展布特征如图9所示，钻遇气层有效厚度为7.8 m，储层压力为15.8 MPa，基质孔隙度为15.6%，渗透率为5.76×10-3 μm2，储层物性较好，含气饱和度为60%，岩石剪切模量为13.5 GPa，泊松比为0.2，参考邻区最小水平主应力为31.3 MPa，地应力差为3.5 MPa。该砂体部署了一口水平井X1-HF井和一口定向井X1-1D井，钻遇率为100%，其中X1-HF井水平段进尺1 066 m，分13段进行压裂改造，水平井根部2~9级压裂点砂体展布范围较大，可加大压裂规模，以提高储层改造体积，压裂缝长不低于150 m。结合地震预测结果可知，在X1-HF井筒附近微裂缝发育一般，但井外远端第2级、第3级、第4级有天然裂缝接触，压裂造长缝的同时易于沟通天然裂缝。X1-HF水平井压裂测试无阻流量达到107×104 m3/d，配产系数为0.17；相邻直井X1-1D压裂1段，测试无阻流量为1.7×104 m3/d，配产系数为0.33。两者支撑剂类型均以30/50目的陶粒为主，能够满足人工裂缝导流能力和抗破碎要求。
图9 鄂尔多斯盆地某致密气藏单砂体展布特征

(a)砂体展布剖面图；(b)砂体展布平面图

Fig.9 Morphology characteristics of single sandbody in tight gas reservoirs of Ordos Basin

基于上述实例数据，针对单砂体采用本文提出的建模方法分别建立考虑裂缝闭合的动态裂缝模型与不考虑裂缝闭合的静态裂缝模型，对致密气藏不同阶段的生产动态进行模拟。动态裂缝模型与静态裂缝模型在返排阶段、开发100 d、开发300 d 3个不同时刻的压力场模拟结果分别如图10和图11所示，可以看出两者在早期的储量动用程度差别不大，从开发100 d开始，动态裂缝模型压力场仍以裂缝线性流为主，而静态裂缝模型已经过渡至缝间径向流、椭圆流阶段，到了开发300 d时刻，静态裂缝模型的储量动用程度要明显大于动态裂缝模型，这是由于静态裂缝模型忽视裂缝在开发过程中的动态闭合导致的。
图10 动态裂缝模型压力场模拟结果

Fig.10 Simulation results of pressure field by dynamic fracture model

图11 静态裂缝模型压力场模拟结果

Fig.11 Simulation results of pressure field by static fracture model

以单缝为研究对象，图12展示了其中第2级人工裂缝及沟通天然裂缝的导流能力变化，可以看出随着开发历程推进，人工裂缝和天然裂缝随着地层孔隙流体压力下降，均出现了一定程度的闭合，第2级人工裂缝导流能力损失主要发生在近井筒位置和裂缝尖端，其相连通的天然裂缝传导率损失以裂缝尖端为主。假设以裂缝传导率数值大小的30%为有效缝长下限，降低至原始数值的30%以下即为无效缝长，通过拟合X1-HF井的生产历史，对水平井每级压裂人工裂缝的有效裂缝半长进行解释。图13为动态裂缝与静态裂缝模型的生产历史拟合结果对比，在其他参数保持一致的前提下，静态裂缝模型对平均半缝长的解释结果为104.5 m，动态裂缝模型的解释结果为88.3 m，从拟合结果来看考虑裂缝尺寸动态变化的裂缝半长更接近于开发实际。考虑到致密气井产量对压裂的依赖性如此之高，裂缝动态闭合造成的产量损失对非常规资源是不可忽略的，由此采用精细化控压生产方式，对减缓裂缝闭合提高气井产量具有重要的现实意义。
图12 第2级人工裂缝及沟通天然裂缝的导流能力变化（返排阶段、开发100 d、开发300 d）

Fig.12 Conductivity changes of 2nd hydraulic fracture and connected natural fracture（flowback stage， 100 d and 300 d in development stage）

图13 动态裂缝与静态裂缝情况下的拟合动态结果对比

Fig.13 Comparison of fitting dynamic results in the case of dynamic fracture and static fracture

6 延伸性讨论

对本文模型进行延伸性讨论，该模型的主要优势表现为：在功能上，能够实现对压裂返排及早期开发阶段人工裂缝动态闭合的定量化表征，同时可以考虑支撑剂属性性质及天然裂缝展布对人工裂缝导流能力的影响；在方法上，半解析模型相较于传统解析解拥有更好的适应性，相比商业数值模拟软件具有更快的求解效率。但二维模型与真实储层条件仍存在一定的差距，无法模拟真三维空间中人工裂缝内部由于重力作用使得支撑剂沉降引起的裂缝垂向形态非均匀变化，此外裂缝闭合会加剧水锁效应，从而影响气井产能。因此，在此本文模型基础上实现真三维裂缝的动态表征与建模，并考虑更深层次的渗流机理和控制因素，是下一步攻关的重点方向。

7 结论

（1）本文结合致密气藏开发实际，提出了适用于模拟压裂液返排和致密气早期开发的渗流—地质力学方程组完全耦合的半解析数学模型及求解方法，能用于捕捉裂缝的动态行为并获取相关重要的裂缝参数；该模型通过拟合压裂返排及早期生产数据，优化生产制度，从而进行更准确的生产动态预测。
（2）由于裂缝成因不同，人工裂缝与天然裂缝在开发过程中有着不同的闭合机制。随着缝内压力下降，人工裂缝会在井筒射孔点、裂缝相交处、裂缝尖端等位置发生不同程度的闭合，而天然裂缝一般仅在裂缝尖端发生闭合。受支撑剂作用的影响，人工缝闭合程度要明显小于天然裂缝。
（3）裂缝闭合造成的产量损失不可忽视，精细控压技术能在一定程度上减小裂缝动态闭合造成的产量损失。一方面，返排初期要控制返排液流速，优化返排工作制度，避免支撑剂回流，最大程度上减小裂缝导流能力的降低幅度；另一方面，返排后期要控制产水速率，减小支撑剂破碎和嵌入带来的应力敏感伤害。此外，在工艺方面可根据井的实际工况，有针对性地考虑重复压裂措施，重塑储层渗流空间，以提高气体渗流能力。

返排及开发早期的有效动用区域位于裂缝附近，基质内的流动可近似于每个区域内的线性流动，同时不考虑各裂缝段之间的干扰，则：

p M i = p I - π q S C F g i B g μ g 2 h a i ϕ M μ g c t M k M t

式中： k M为基质渗透率，×10-3 μm2；φ M为基质孔隙度，无因次；ct M为基岩总压缩系数，MPa-1； p I为气藏初始压力，MPa。

变流量条件下的离散格式为：

p M i n + 1 = p I - π B g μ g h Δ L F i ϕ M μ g c t M k M ∑ k = 1 n + 1 q S C F g i k - q S C F g i k - 1 t n + 1 - t k - 1

T、α和P׳ cgw i，j 的表达式为：

T g i , j n + 1 = G i , j k r g i , j n + 1 1 μ g B g i , j n + 1
T w i , j n + 1 = G i , j k r w i , j n + 1 1 μ w B w i , j n + 1
α i g 1 n + 1 = 2 a i h Δ t n + 1 S F g n
α i w 1 n + 1 = 2 a i h Δ t n + 1 1 - S F g n
α i g 2 n + 1 = 2 a i h Δ t n + 1 E B g i n
α i w 2 n + 1 = - 2 a i h Δ t n + 1 E B w i n
P c g w i , j ' = P c g w i n + 1 - P c g w j n + 1 S F g i n + 1 - S F g j n + 1
q S C F g i n + 1 = q ˜ S C F g i n + 1 V b i
q S C W g i n + 1 = q ˜ S C W g i n + 1 V b i
q S C W w i n + 1 = q ˜ S C W w i n + 1 V b i

式中： Gi，j 为网格 i和网格 j之间的几何导流能力，μm2·m。

Gi，j 可采用调和平均的方法求得：

G i , j = γ i γ j γ i + γ j

式中： γi 为网格i的导流能力，μm2·m；γj 为网格j的导流能力，μm2·m。

γi 的表达式为：

γ i = k F l w F i 2 a i h

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
1
贾爱林， 位云生， 郭智， 等. 中国致密砂岩气开发现状与前景展望［J］. 天然气工业， 2022， 42（1）：83-92.

JIA A L， WEI Y S， GUO Z， et al. Development status and prospect of tight sandstone gas in China［J］. Natural Gas Industry， 2022， 42（1）：83-92.

2
李宪文， 王历历， 王文雄， 等. 基于小井眼完井的压裂关键技术创新与高效开发实践——以苏里格气田致密气藏为例［J］. 天然气工业， 2022， 42（9）：76-83.

LI X W， WANG L L， WANG W X， et al. Innovation and efficient development practice of key fracturing technologies based on slim-hole completion：A case study of tight gas reservoir in Sulige Gasfield［J］. Natural Gas Industry，2022，42（9）：76-83.

3
陈诚， 雷征东， 房茂军， 等. 致密砂岩储层可压性评价与极限参数压裂技术［J］. 科学技术与工程， 2022， 22（16）：6400-6407.

CHEN C， LEI Z D， FANG M J， et al. Tight sandstone reservoir compressibility evaluation and limit parameter fracturing technology［J］. Science Technology and Engineering，2022，22（16）：6400-6407.

4
WANG J， ELSWORTH D. Role of proppant distribution on the evolution of hydraulic fracture conductivity［J］. Journal of Petroleum Science & Engineering， 2018， 166：249-262.

5
杜旭林， 程林松， 牛烺昱， 等. 考虑水力压裂缝和天然裂缝动态闭合的三维离散缝网数值模拟［J］.计算物理，2022，39（4）：453-464.

DU X L， CHENG L S， NIU L Y， et al. Numerical simulation of 3D discrete fracture networks considering dynamic closure of hydraulic fractures and natural fractures［J］.Chinese Jo-urnal of Computational Physics， 2022， 39（4）：453-464.

6
ABBASI M A，DEHGHANPOUR H，HAWKES R V. Flowback Analysis for Fracture Characterization［C］. SPE Canadian Unconventional Resources Conference， 30 October-1 November， Calgary， Alberta， Canada， 2012.

7
SUN Z L， CHENG L S， DU X L， et al. Typical Curve and Diagnosis Method for Identifying Fracture Closure Points of Fractured Wells in Flowback and Early-Time Production Period for Tight Oil Reservoir：A Field Example from Ordos Basin in China［C］. SPE Annual Technical Conference and Exhibition， 3-5 October， Houston， Texas， USA， 2022.

8
虞绍永. 基于早期返排历史数据的水平井分段压裂效果评价方法［J］. 石油钻探技术，2021， 49（6）：1-7.

YU S Y. Post-frac evaluation of multi-stage fracturing on horizontal wells based on early flowback history［J］.Petroleum Dri-lling Techniques， 2021， 49（6）：1-7.

9
严谨， 程时清， 郑荣臣， 等. 确定压裂裂缝部分闭合的现代产量递减分析方法及应用［J］. 石油钻采工艺， 2018， 40（6）：787-793.

YAN J， CHENG S Q， ZHENG R C， et al. Development and application of the modern production decline analysis method in consideration of partial closure of hydraulic fracture［J］.Oil Dri-lling & Production Technology， 2018， 40（6）：787-793.

10
CLARKSON C R，WILLIAMS-KOVACS J D. A New Method for Modeling Multi-Phase Flowback of Multi-Fractures Horizontal Tight Oil Wells to Determine Hydraulic Fracture Properties［C］. SPE Annual Technical Conference and Exhibition，30 September-2 October，New Orleans，Louisiana，USA， 2013.

11
WILLIAMS-KOVACS J D，CLARKSON C R.Stochastic Mo-deling of Two-Phase Flowback of Multi-Fractured Horizontal Wells to Estimate Hydraulic Fracture Properties and Forecast Production［C］.SPE Unconventional Resource Conference， 10-12 April， Woodlands， Texas， USA， 2013.

12
KANFAR M S， CLARKSON C R. Reconciling flowback and production data： A novel history matching approach for liquid rich shale wells［J］. Journal of Natural Gas Science & Engineering， 2016， 33：1134-1148.

13
陈希. 页岩气藏压裂水平井返排模拟［D］. 成都：西南石油大学， 2019.

CHEN X. Fracturing Fluid Flowback Simulation of Fractured Horizontal well in Shale Gas Reservoirs［D］. Chengdu：Southwest Petroleum University， 2019.

14
CLARKSON C R，QANBARI F，WILLIAMS-KOVACS J D. Semi-analytical model for matching flowback and early-time pro-duction of multi-fractured horizontal tight oil wells［J］.Journal of Unconventional Oil & Gas Resources，2016（15）：134-145.

15
CHENG L S， JIA P， RUI Z H， et al. Transient responses of multifractured systems with discrete secondary fractures in unconventional［J］. Journal of Natural Gas Science & Engineering， 2017（41）：49-62.

16
JIA P， CHENG L S， CLARKSON C R， et al. A novel method for interpreting water data during flowback and early-time production of multi-fractured horizontal wells in shale reservoirs［J］.International Journal of Coal Geology，2018（200）：186-198.

17
JIA P， CHENG L S， HUANG S J， et al. Dynamic coupling of analytical linear flow solution and numerical fracture model for simulating early-time flowback of fractured tight oil wells （planar fracture and complex fracture network）［J］. Journal of Petroleum Science & Engineering，2019，177：1-23.

18
JIA P， MA M， CHENG L S， et al. A semi-analytical model for capturing dynamic behavior of hydraulic fractures during flowback period in tight oil reservoir［J］. Energy Science & Engineering， 2020， 8（10）：3415-3440.

19
JIA P， MA M， CHENG L S， et al. Capturing Dynamic Behavior of Propped and Unpropped Fractures During Flowback and Early-time Production of Shale Gas Wells Using a Novel Flow-geomechanics Coupled Model： A field example from the ChangNing shale in China［C］.Unconventional Resources Tech-nology Conference（URTeC）， 20-22 July， Denver， Colorado， USA， 2020.

20
FU Y， DEHGHANPOUR H， EZULIKE D O， et al. Estimating effective fracture pore volume from flowback data and evaluating its relationship to design parameters of multistage-fracture completion［J］. SPE Production & Operations， 2017， 32（4）： 423-439.

21
ZANGANEH B，CLARKSON C R.Reinterpretation of Flow Patterns During DFITs Based on Dynamic Fracture Geometry，Leakoff and Afterflow［C］.SPE Hydraulic Fracturing Technology Conference & Exhibition，23-25 January， Woodlands， Texas， USA， 2018.

22
ZHANG F， EMAMI-MEYBODI H. Flowback Fracture Closure of Multifractured Horizontal Wells in Shale Gas Reservoirs［C］. SPE Eastern Regional Meeting，7-11 October， Pittsburgh， Pennsylvania， USA， 2018.

23
WATTENBARGER R A，EL-BANBI A H，VILLEGAS M E， et al. Production Analysis of Linear Flow into Fracture Tight Gas Wells［C］. SPE Rocky Mountain Regional/Low Permeability Reservoirs Symposium and Exhibition， 5-8 April， Denver， Colorado， USA， 1998.

24
BARREE R D， MISKIMINS J L， CONWAY M W， et al. Generic Correlations for Proppant-pack Conductivity［C］. SPE Hydraulic Fracturing Technology Conference， 9-11 February， Woodlands， Texas， USA， 2016.

25
WITHERSPOON P A， WANG J S， IWAI K， et al. Validity of cubic law for fluid flow in a deformable rock fracture［J］. Water Resources Research， 1980， 16（6）：1016-1024.

26
LEE H S， CHO T F. Hydraulic characteristics of rough fractures in linear flow under normal and shear load［J］. Rock Mechanics & Rock Engineering， 2002， 35（4）：299-318.

27
WANG H， SHARMA M M. Modeling of hydraulic fracture closure on proppants with proppant settling［J］. Journal of Petroleum Science & Engineering， 2018， 171：636-645.

28
MCCLURE M W， BABAZADEH M， SHIOZAWA S. Fully Coupled hydromechanical simulation of hydraulic fracturing in 3D discrete-fracture networks［J］.SPE Journal，2000，21（4）：1302-1320.

29
SHOU K J， CROUCH S L. A higher order displacement discontinuity method for analysis of crack problems［J］. International Journal of Rock Mechanics & Mining Sciences， 1995， 32（1）：49-55.

30
KIM J， TCHELEPI H， JUANES R. Stability， accuracy， and efficiency of sequential methods for coupled flow and geomechanics［J］. SPE Journal， 2011， 9（2）：227-236.

31
SNEDDON I N. The distribution of stress in the neighborhood of a crack in an elastic solid［J］. Proceedings of the Royal Society A， 1946， 187（1009）：229-260.

Options
文章导航

/

〈 〉

陇ICP备2021001824号-7　 甘公网安备 62010202000678号
版权所有 © 《天然气地球科学》编辑部
地址：甘肃省兰州市天水中路8号　
邮编：730000　
电话：(0931)8277790　
E-mail：geogas@lzb.ac.cn
总访问量 　 今日访问 　 在线人数
技术支持：北京玛格泰克科技发展有限公司