0 引言
1 基于改进的Hebb神经网络主分量分析的均一反射层提取方法
1.1 方法原理
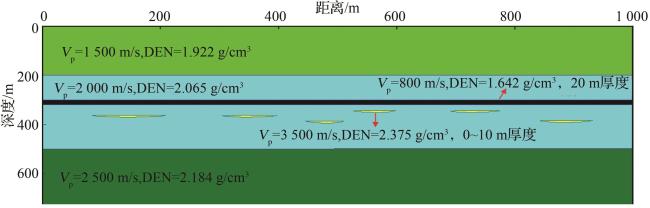
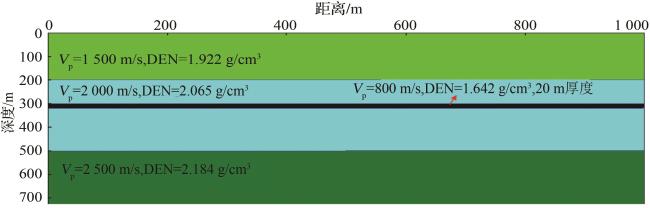
1.2 二维模型试算
2 实际资料分析
2.1 原始地震数据Wheeler域变换
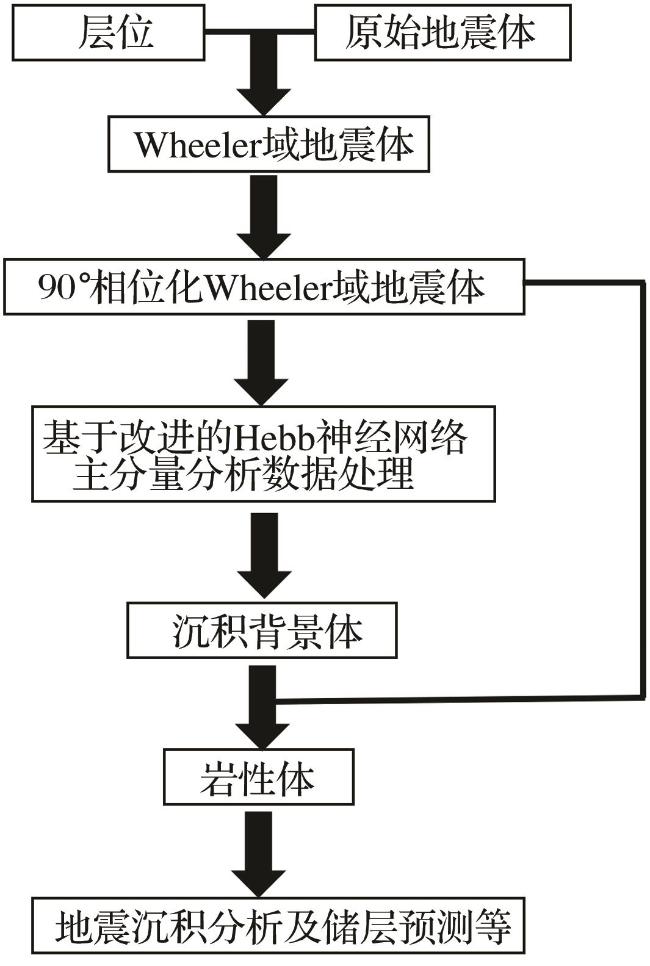
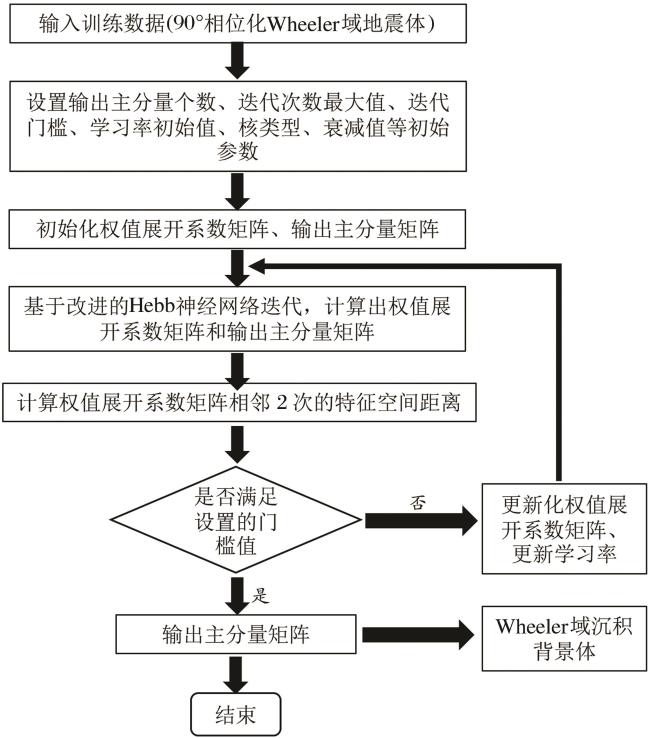
2.2 基于改进的Hebb神经网络主分量分析的均一反射层体提取流程
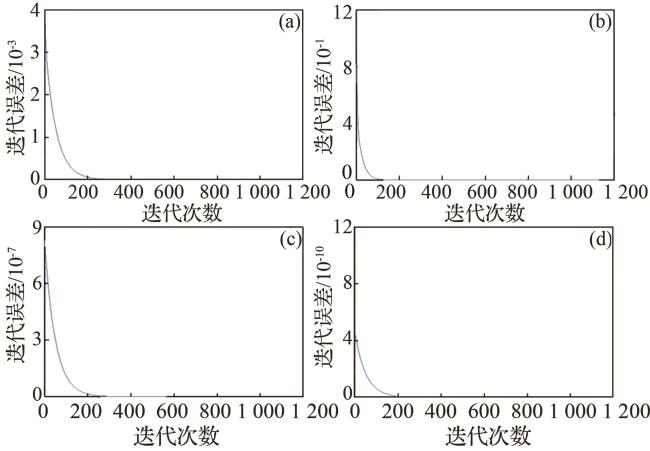
2.3 核函数选择
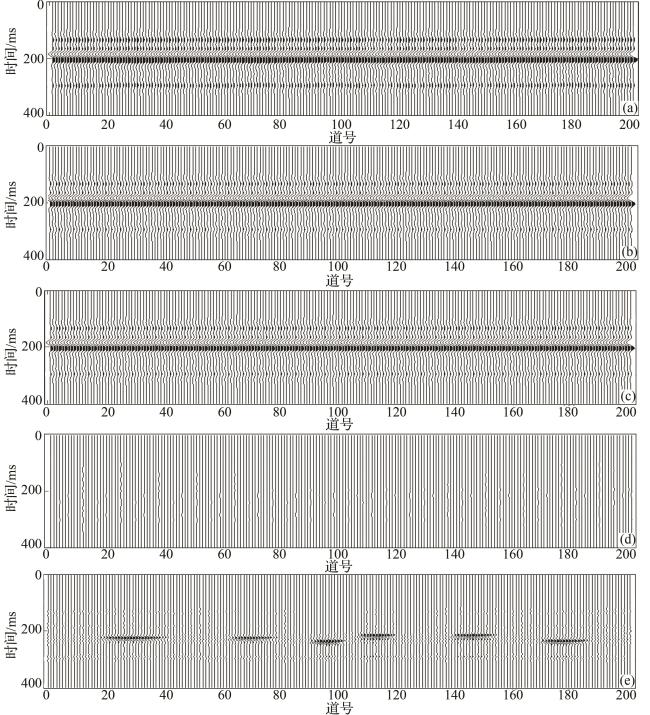
图7 四种核函数迭代收敛次数比较(a)线性核函数d=1,文献[12]所用方法;(b)多项式核函数d=2; (c)高斯核函数 为8 000;(d)Ricker子波核函数f=0.000 05 Fig.7 Comparison diagram of four kinds of kernel function iteration convergence times |
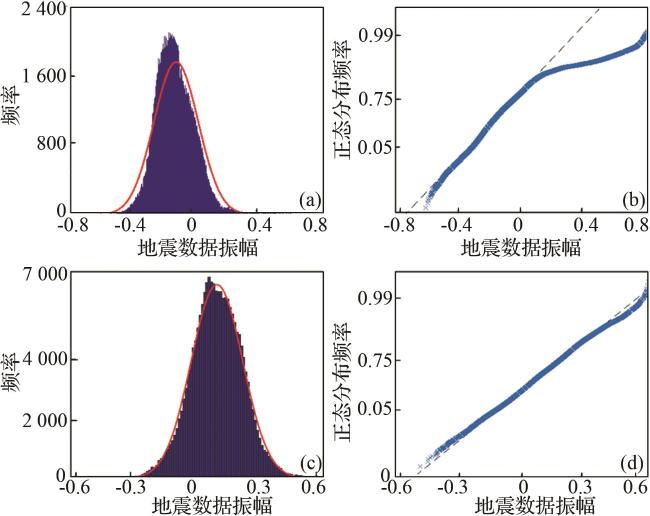
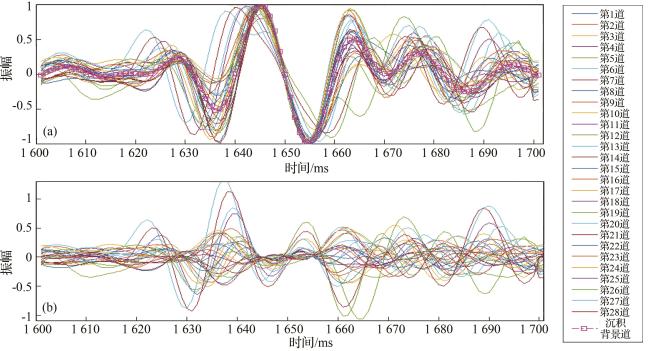
图8 Wheeler域90°相位化地震体和Wheeler域岩性体数据分布比较(a) Wheeler域90°相位化地震体第14个采样点频率直方图;(b) Wheeler域90°相位化地震体第14个采样点正态分布概率;(c)Wheeler域岩性体第14个采样点频率直方图;(d) Wheeler域岩性体第14个采样点正态分布概率 Fig.8 Comparison of the data distribution of the 90° phased seismic body in the Wheeler domain and the lithological body in the Wheeler domain |
2.4 权值展开系数衰减项 和学习率步长衰减 确定
表1 KHA与MKHA迭代速度及收敛精度比较Table 1 Comparison of iteration speed and convergence accuracy between KHA and MKHA |
| 参数 | KHA | MKHA( ) | MKHA( ) | MKHA( 、 ) |
|---|---|---|---|---|
| 迭代次数 | 148 | 167 | 159 | 198 |
| 收敛精度/10-12 | 13.764 39 | 9.869 88 | 9.980 63 | 9.844 79 |
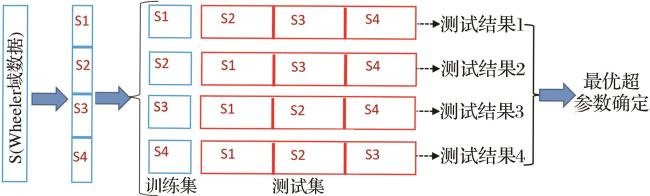
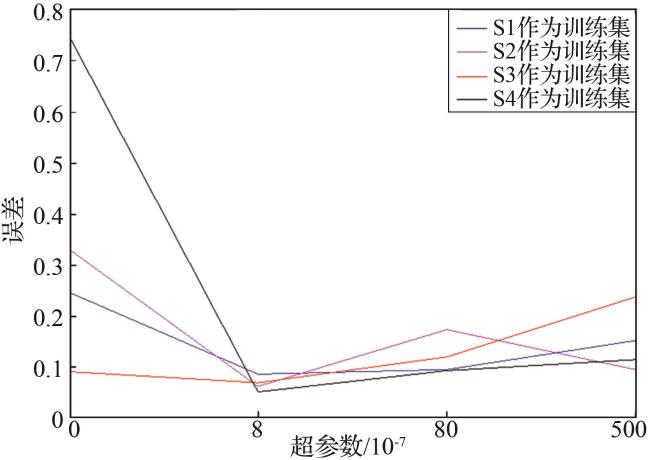
2.5 超参数f确定
2.6 A工区应用效果
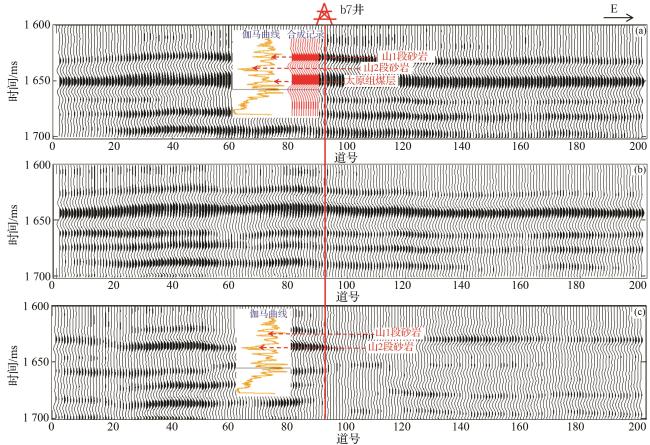
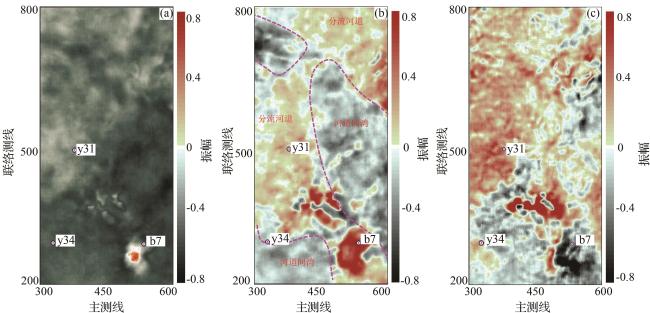
图12 Inline534测线Wheeler域地震剖面、90°相位化Wheeler域地震剖面和Wheeler域岩性体剖面比较(a)Inline534测线过b7井Wheeler域地震剖面;(b)Inline534测线过b7井90°相位化Wheeler域地震剖面;(c)Inline534测线过b7井岩性体剖面 Fig.12 Comparison of Inline534 Wheeler domain seismic section, 90° degree phased Wheeler domain seismic section and Wheeler domain lithology section |



 甘公网安备 62010202000678号
甘公网安备 62010202000678号