天然气地球科学 >

2021 , Vol. 32 >Issue 2: 274 - 287

DOI: https://doi.org/10.11764/j.issn.1672-1926.2020.09.002

天然气开发

改进的页岩气五区复合产能模型及其影响因素

  • 许莹莹 , 1, 2 ,
  • 胡志明 1, 2 ,
  • 端祥刚 1 ,
  • 常进 1 ,
  • 张彦从 1, 2
展开
  • 1. 中国石油勘探开发研究院，河北 廊坊 065007
  • 2. 中国科学院大学渗流流体力学研究所，河北 廊坊 065007

许莹莹（1995-）,女,湖北荆门人，硕士研究生，主要从事页岩渗流模型与产能评价研究.E-mail:.

收稿日期: 2020-06-20

  修回日期: 2020-08-14

  网络出版日期: 2022-03-17

收起

Shale gas improved five-zone composite productivity prediction model and its influencing factors

  • Ying-ying XU , 1, 2 ,
  • Zhi-ming HU 1, 2 ,
  • Xiang-gang DUAN 1 ,
  • Jin CHANG 1 ,
  • Yan-cong ZHANG 1, 2
Expand
  • 1. PetroChina Research Institute of Petroleum Exploration and Development，Langfang 065007，China
  • 2. Institute of Porous Flow and Fluid Mechanics，University of Chinese Academy of Sciences，Langfang 065007，China

Received date: 2020-06-20

  Revised date: 2020-08-14

  Online published: 2022-03-17

Supported by

The China National Science and Technology Major Project(2017ZX05037-001)

Fold

本文亮点

产能是评价页岩气田开发效果的核心指标，其中页岩气高压物性、超临界解吸、多重微观流动机理以及应力敏感性的综合非线性效应对产能的贡献程度不可忽略。由于前人提出的产能模型考虑的非线性影响较为单一，关于综合研究非线性因素对产能贡献的研究成果较少，因此基于常规五区复合线性流模型，耦合了气体的非线性效应和缝网应力敏感性，建立了改进的复合线性流模型并得到产能半解析解，通过实例验证产能解的可靠性和明确优化了影响产能的重要因素。结果表明：①该模型综合考虑气体产出过程中非线性效应对产量的影响，计算精度大幅提高，可合理评价预测气井中长期的产能大小；②裂缝半长越大，产能越大，应尽可能造长缝；主裂缝簇间距和导流能力过高或者过低，储层的动用程度变化不明显，主裂缝簇间距和导流能力取值可分别优选在10 m左右和 4.0 × 10 - 15 m3左右。应力敏感系数越大，产能越低，压裂过程应优选性能优良的支撑剂或设计裂缝面滑移以提高裂缝导流能力；③水平井巷道间距和水平段长度对于提高储层动用程度效果是可观的，在实际生产中巷道间距可优选500 m，同时建议可适量部署长度2 000~3 000 m的水平井进行技术攻关。研究成果可紧密联系现场开发，合理评价预测产能及指导优化压裂设计参数以最大限度提高页岩气采收率，具备一定的理论意义和工程价值。

本文引用格式

许莹莹 , 胡志明 , 端祥刚 , 常进 , 张彦从 . 改进的页岩气五区复合产能模型及其影响因素[J]. 天然气地球科学, 2021 , 32(2) : 274 -287 . DOI: 10.11764/j.issn.1672-1926.2020.09.002

Highlights

Productivity is the core index to evaluate the development effect of shale gas field， and the comprehensive nonlinear effect of high-pressure physical property， supercritical desorption， multiple micro-flow mechanism and stress sensitivity of shale gas can’t be ignored in its contribution to productivity. In this paper， based on the conventional five-zone compound flow model， a comprehensive consideration was given to gas nonlinearity and the stress sensitivity， an improved compound linear flow model was established and a semi-analytical solution for productivity was obtained. Then， the reliability of productivity solution was verified through examples and important influencing factors were clarified. The results indicated： （1）The model comprehensively considers the impact of nonlinear effects on gas production so as to predict the medium- and long-term productivity of gas wells accurately. （2）The greater the main fracture half-length， the greater the productivity， so long fractures should be designed as much as possible； too high or too low the cluster spacing and conductivity of the main fractures do not significantly change the extent of reservoir utilization， so the values of the cluster spacing and conductivity of the main fractures in this paper can be preferably around 10 m and around 4.0×10-15 m3； the greater the stress sensitivity coefficient， the lower the productivity， and the proppant with excellent performance should be selected or the fracture slip surface should be designed to improve the fracture conductivity. （3）The significance of horizontal well spacing and horizontal well length on improving the utilization of shale reservoirs is considerable. In actual production， the horizontal well spacing can be optimized to 500 m， and horizontal well length of 2 000-3 000 m can also be adopted for technical research.

0 引言

页岩气是自生自储于暗色泥页岩或高碳泥页岩中的非常规天然气，分布范围广、储量丰富、开发潜力大，在全球能源结构中的地位日益重要［1］。产能是评价页岩气田开发效果的核心指标，确定准确高效的产能预测方法需要准确评价地层条件下甲烷的高温吸附特征和明确页岩气体在微纳米孔隙的多重非线性运移机制，旨在最大限度提高页岩气藏开发程度。页岩吸附气含量占总气体含量的 20%~85%，页岩气生产后期的产气量多由基质内的解吸气贡献。实验［2-4］研究和理论［5-7］推导证明了地层条件下的甲烷在页岩储层的吸附规律为超临界吸附，常规Langmuir吸附方程并不适用于描述等温线高压段的吸附现象，在此基础上完善了储层条件下吸附气量评价方法，针对性地建立了一系列成熟的超临界吸附模型，计算精度大幅提高。此外，微纳米孔中页岩气非线性流动机理的理论认识也逐渐完善，一致认为页岩气藏开发生命周期中气体的流动机理复杂，可包括滑脱流，扩散等非线性流动，并且页岩基质微纳米孔隙中的流态不可能是单一运移机制控制的，而应该是多种流动机制协同贡献的结果，并先后提出了揭示微纳米尺度气体微观渗流规律的表观渗透率模型［8-11］。
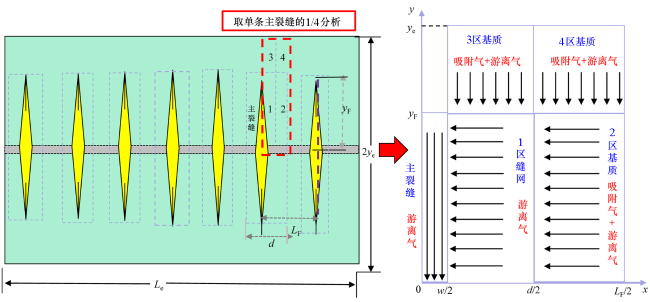
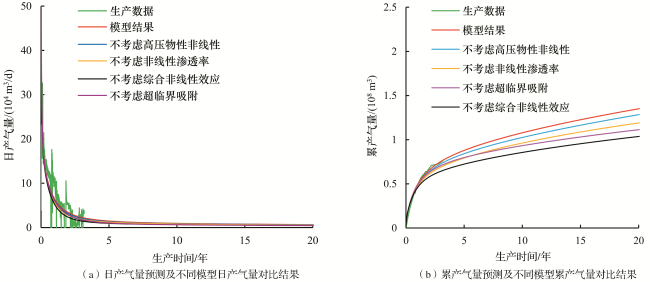
国内外学者开展了大量页岩气井生产过程中的压力动态分析和产能预测的研究并针对性地提出了许多不同的模型。EL-BANBIAN［12］考虑基质到裂缝、裂缝到井筒均为达西线性渗流，建立双孔瞬态线性流动模型。AHMADI等［13］建立了有机基质—基质微孔隙—天然裂缝三重介质达西流模型，BROWN等［14-15］在2009年给出了考虑主裂缝间区域均被改造的多段压裂水平井的三线性流模型，接着在2011年考虑外区的供气能力并提出了页岩气井三线性流模型。郭小哲等［16］基于经典三线性流模型提出了考虑解吸扩散的渗流模型并得到了产能解析解以及井底压力公式。吴永辉等［17］考虑了气体的解吸、扩散、滑脱以及高压物性的非线性建立了三线性流模型并获取了产能半解析解。STALGOROVA［18］考虑主裂缝间和主裂缝外区的未压裂储层动用过程的渗流场的差异， 建立了五区复合线性流模型。尹洪军等［19］在Stalgorova 建立的五区复合模型的基础上完善建立了耦合页岩气解吸、扩散的产能预测模型并研究了产能的影响因素。文献调研结果表明以上传统的线性流模型多受限于气井中前期的线性流阶段，无法准确描述生产后期基质供给阶段的生产特征，且部分改进的线性流产能模型考虑气体的非线性因素较为单一，多忽略气体产出过程中高压物性、超临界解吸、流动规律等多种综合非线性效应对气井的生产规律的影响而严重低估气井产能大小。
针对现有研究不足，在常规五区复合渗流模型的基础上，综合考虑了高压物性非线性、过剩量修正的超临界吸附模型、引入了储层低压下的扩散、滑脱的表观渗透率模型以及次生缝网中指数形式的应力敏感性模型建立了改进的五区复合渗流模型，主要采取Laplace变换、Stehfest数值反演和牛顿迭代方法得到了模型的产能半解析解，通过威远区块某气井的生产数据验证产能解的可靠性并明确、优化产能重要影响因素，为准确评价预测产能及最大限度的增加资源采出程度提供理论依据。

1 物理模型

由于页岩储层天然裂缝、脆性矿物含量及地应力等因素的复杂性以及储层改造后压裂裂缝形态呈多样化特点，描述基质和裂缝非均质性特征参数无法准确获取，因此本文假设主裂缝形态可用平板双翼模型表征 ［20］，裂缝网络与基质区域处理成等效介质。考虑到主裂缝间以及主裂缝外区域存在部分未压裂的储层，不同区域的渗流特征存在明显差异，物理模型选取单条主裂缝的1/4，将该模型分为以下5部分：内区主裂缝、缝网1区、主裂缝间基质2区，以及外区未压裂基质3区和基质4区（图1）。
图1 页岩气多簇压裂水平井五区复合简化物理模型

Fig.1 Simplified five-zone composite physical model of multi-fractured shale gas horizontal well

具体假设为：
（1）页岩气各自从外区3区、4区流入内区1区、2区，2区内的气体经1区、主裂缝向井筒汇聚，单相甲烷气体在不同渗流场中的运移是一维渗流过程，页岩储层半宽为 y e，封闭外边界均质等厚。
（2）未压裂改造基质2、3、4区域中吸附气服从超临界Langmuir吸附方程，考虑游离气在基质中的扩散、滑脱效应。
（3）内区缝网1区中游离气以线性流的形式向主裂缝传质，考虑缝网应力敏感性。
（4）内区主裂缝均匀分布、等长且上下对称，垂向上完全压开储层，半长为 y F，主裂缝宽度为 w，主裂缝簇间距为 L F，单裂缝的压裂半宽大小为 d / 2，气体流动行为遵循达西定律。
（5）气体在不同渗流区域间的窜流为非稳态流，气体产出过程为等温渗流，忽略重力和毛细管力的影响，气井以定压生产。

1.1　高压物性参数

由于渗流控制方程中气体高压物性参数随温压条件变化较大，非线性效应不可忽略［17］。为简化方程求解过程，本文引用拟压力和拟时间［21］对控制方程进行线性化处理。
拟压力表达式为：
ψ = ∫ 0 P 2 P μ Z d P
拟时间表达式为：
t a = ∫ 0 t μ i C t i μ ( P ) C t ( P ) d t
式中： ψ为拟压力， Pa2/（Pa·s）； t a为拟时间，s；   μ i为初始时刻的气体黏度值，Pa·s； μ ( P )为任意压力下的气体黏度值，Pa·s； C t i为初始时刻的综合压缩系数，Pa-1； C t ( P )为任意压力下的综合压缩系数，Pa-1。

1.2　气体密度

根据真实气体的状态方程可分别得到游离相气体在渗流区域中的密度：
ρ g = P M Z R T
式中： P为渗流场压力，Pa；ρ g表示渗流区域游离相气体密度，kg/m3； M为甲烷气体摩尔质量，g/mol，取16 g/mol； Z为气体偏差因子，无量纲； R为普适气体常数，取值8.314 J/（mol·K）； T为储层温度，K。

1.3　气体超临界吸附—解吸模型

气体吸附—解吸过程是可逆的，可以用吸附模型来描述储层生产过程中页岩气的解吸特征。由于地层条件下甲烷的高压等温吸附曲线不再是一条单调递增的曲线，常规的Langmuir方程无法拟合页岩等温吸附规律，本文采用基于吸附相体积理论建立的过剩量高压等温吸附模型［2］：
q a d = P s c M Z s c R T s c V L P i P i + P L ( 1 - ρ g ρ a )
式中：q ad为单位基质体积页岩气超临界过剩吸附量，kg/m3；   P s c为地面标准大气压，取值0.101 MPa；   T s c指标准状态的温度，取值273.15 K； Z s c为理想气体的压缩因子，取值1，无量纲；   V L为Langmuir体积，m3/m3；   P L为Langmuir压力，Pa；   P i为基质压力，Pa（i=2、3、4）；ρ a为吸附相密度，kg/m3。

1.4　表观渗透率模型

低渗储层基质微纳米孔隙较为发育，孔隙结构复杂，储层开发后期整体压力较低，气体在基质中的流动规律已明显偏离达西方程，扩散和滑脱等非线性流动效应明显［11］，本文采用JAVADPOUR［10］提出的经典表观渗透率模型描述基质中气体的扩散、滑脱等微观渗流机制：
K i a = c D g i μ i + F i K i
滑移速度校正因子：
F i = 1 + 8 π R T M μ ( i ) × 10 - 3 P a v g × 10 6 r i ( 2 α - 1 )
水力流动半径为：
r i = 8 K i φ i
式中： F i为滑移速度校正因子，无量纲； φ i为基质区孔隙度，无量纲； μ ( i )为不同基质区域的气体黏度值，Pa·s； K i a为基质区域的表观渗透率，m2；   K i为达西渗透率，m2；   r i为圆形毛管半径，m；   P a v g为气体平均压力，Pa； α为切向动量协调系数，取决于孔隙内壁光滑度、气体类型、温度、压力等，其取值范围为0~1，本文取值0.8； D为扩散系数，单位为m2/s；下标i=2、3、4代表3个基质区域。

1.5　压力敏感效应

由于游离相气体从缝网产出时，地层压力不断降低，无支撑剂次生裂缝可能存在闭合的现象，次生缝网渗透率会明显降低，因此本文引入拟渗透率模量［22］至指数形式的应力敏感性经验模型［23］，表征次生裂缝的应力敏感性对气体在缝网中流动能力的影响：
K f = K f i e - γ ( ψ i - ψ f )
式中：Kf为考虑压敏效应后的内区缝网渗透率，m2；Kfi为初始时刻的内区缝网渗透率，m2； γ为拟渗透率模量，（Pa·s）/Pa2； ψ i为储层初始地层拟压力， Pa2/（Pa·s）； ψ f为储层缝网拟压力，Pa2/（Pa·s）。

2 渗流数学模型

2.1　4区基质渗流方程

4区基质气体沿y方向以非稳态窜流的方式汇入2区基质，考虑页岩基质中吸附气的超临界解吸过程和气体在页岩纳米孔隙中的扩散、滑脱， 外边界条件为封闭， 内边界压力连续。
根据质量守恒定律可得基质渗流控制方程：
∂ ( ρ g φ 4 ) ∂ t + ∂ ( 1 - φ 4 ) q a d ∂ t = - ∂ ∂ y ( ρ g v 4 )
气体在基质的渗流速度可由运动方程得到：
v 4 = - K 4 a μ 4 ∂ P 4 ∂ y
结合式（4），对式（9）左端变形：
∂ ρ g φ 4 ∂ t + ∂ ( 1 - φ 4 ) q a d ∂ t = ρ g φ 4 ( 1 φ 4 ∂ φ 4 ∂ P 4 + 1 ρ g ∂ ρ g ∂ P 4 ) ∂ P 4 ∂ t + ( V L ( 1 - φ 4 ) T Z P s c φ 4 Z s c T s c P L P 4 ( P 4 + P L ) 2 ( 1 - ρ g ρ a ) ) ∂ P 4 ∂ t
上式中不考虑地层压缩的影响，定义游离相压缩系数和超临界解吸压缩系数：
C g 4 = 1 ρ g ∂ ρ g ∂ P 4
C d 4 = V L ( 1 - φ 4 ) T Z P s c φ 4 Z s c T s c P L P 4 ( P 4 + P L ) 2 ( 1 - ρ g ρ a )
将过剩吸附量以解吸压缩系数的形式［22］加入到外区基质综合压缩系数中，因此得到外区基质综合压缩系数C t4：
C t 4 = C g 4 + C d 4
联立式（12）、式（13）和式（14）代入式（11），则式（11）可以变形为：
∂ ρ g φ 4 ∂ t + ∂ ( 1 - φ 4 ) q a d ∂ t = ρ g φ 4 C t 4 ∂ P 4 ∂ t
将式（10）、式（15）代入式（9），则：
ρ g φ 4 C t 4 ∂ P 4 ∂ t = ∂ ∂ y ( ρ g K 4 a μ 4 ∂ P 4 ∂ y )
初始时刻外区渗流场压力等于原始地层压力：
P 4 ( t = 0 ) = P e
外边界：
∂ P 4 ∂ y y = y e = 0
内边界：
P 4 ( y = y F ) = P 2 ( y = y F )
式中：vi（i=2、3、4）为基质渗流速度，m/s； y e为外边界距离值，m； C d i为修正的超临界解吸气体压缩系数，Pa-1； C g i为气体压缩系数，Pa-1；C t i为基质综合压缩系数，Pa-1。

2.2　3区基质渗流方程

与4区基质气体的渗流规律类似，3区基质中的气体沿y方向以扩散、滑脱和非稳态窜流的方式汇入1区基质，根据质量守恒方程、运动方程和状态方程可推导得到3区基质渗流方程：
ρ g φ 3 C t 3 ∂ P 3 ∂ t = ∂ ∂ y ( ρ g K 3 a μ 3 ∂ P 3 ∂ y ) P 3 ( 0 , y ) = P e ∂ P 3 ∂ y y = y e = 0 P 3 ( y = y F ) = P 1 ( y = y F )

2.3　2区基质渗流方程

考虑2区基质中的气体沿x方向流入1区基质，流动规律为扩散、滑脱，外边界封闭，内边界2区和1区压力连续，建立2区基质渗流方程：
∂ ρ g φ 2 ∂ t = ∂ ∂ x ρ g K 2 a μ 2 ∂ p 2 ∂ x + 2 Q 24
单位时间内气体从4区基质向2区缝网运移的非稳态窜流质量通量大小为［24］：
Q 24 = ρ g K 4 a μ 4 y F ∂ P 4 ∂ y y = y F
外边界采用非流量边界，内边界缝网压力和主裂缝压力相等，初始时刻缝网渗流场压力为原始地层压力，则初边界条件表示为：
初始条件为：
P 2 ( t = 0 ) = P e
外边界为：
∂ P 2 ∂ x x = L f / 2 = 0
内边界为：
P 2 ( x = d 2 ) = P 1 ( x = d 2 )
式中： Q 24为4区基质向2区基质的窜流量， k g / ( m 3 ⋅ s )。

2.4　1区缝网渗流方程

1区缝网中的气体以线性流的方式沿x方向向井筒汇聚，考虑应力敏感性对缝网渗透率的影响，外边界与2区流量连续，内边界与主裂缝的压力连续。根据质量守恒方程、运动方程和状态方程可推导得到1区基质渗流方程：
∂ ρ g φ 1 ∂ t = ∂ ∂ x ρ g K 1 μ 1 ∂ p 1 ∂ x + 2 ρ g K 3 a μ 3 y F ∂ P 3 ∂ y y = y F P 1 ( t = 0 ) = P e ∂ P 1 ∂ x x = d 2 = K 2 a μ 1 K 1 μ 2 ∂ P 1 ∂ y x = d 2 P 1 ( x = 0 ) = P F ( x = 0 )
式中：P F为内区主裂缝压力值，Pa。

2.5　内区主裂缝渗流方程

考虑气体在主裂缝中以线性流的方式向井筒传输气体，基于气体质量守恒定律和运动方程建立主裂缝渗流控制方程：
∂ ρ g φ F ∂ t = ∂ ∂ y ρ g K F μ F ∂ p F ∂ y + 2 Q 1 F
式中： Q 1 F为内区次生缝网和主裂缝间在单位时间内的窜流量［24］：
Q 1 F = ρ g K 1 μ F x L ∂ P 1 ∂ x x = d / 2
考虑气井定井底压力生产，外边界封闭，则主裂缝的初边界条件为：
初始条件：
P F ( t = 0 ) = P e
外边界： ∂ P F ∂ y x = y F = 0
∂ P F ∂ y x = y F = 0
内边界：
P F ( y = 0 ) = P w f
式中： φ F为内区主裂缝孔隙度，无量纲；μ F为内区主裂缝中气体的黏度值，Pa·s；Q 1F为内区缝网向内区主裂缝的窜流量，kg/（m3·s）；P wf为井底压力值，Pa；K F为内区主裂缝渗透率值，m2。
依据表1中无因次参数定义，将渗流控制方程组转化为无因次量纲化的渗流方程，以便于求解无因次产能模型。
表1 无因次参数定义

Table 1 The definition of dimensionless parameters

无因次参数 定义式 无因次参数 定义式
无因次拟压力 ψ D = ψ i - ψ ψ i - ψ w f 无因次产量 1 q D = T s c K F A c w ( ψ i - ψ w f P s c q s c T
无因次拟时间 t a D = K F t a μ ( φ 1 C t 1 + φ 2 C t 2 + φ F C t F ) A c w 储容比 w i = ψ i C t i φ F C t F + φ 1 C t 1 + φ 2 C t 2（i=1、2、F）
无因次长度 x D = 2 x L f y D = y A c w 3-1区传质系数 λ 1 i = 12 K i L F 2 K 1 A c w(i=2、3)
3区传导系数 η 3 D = K F φ 1 C t 1 + φ 2 C t 2 + φ F C t F φ 3 C t 3 K 3 a 4-2区传质系数 λ 2 i = 12 K i L F 2 K 2 A c w(i=4、F)
4区传导系数 η 4 D = K F φ 1 C t 1 + φ 2 C t 2 + φ F C t F φ 4 C t 4 K 4 a 1-F区传质系数 λ 1 F = 12 K 1 L F 2 K F A c w
无因次压敏系数 γ f D = γ f ( ψ i - ψ w f 无因次储层导流能力 R C D = K 1 d D K 2 L F
则页岩气井无因次渗流数学方程为：
4区基质控制方程：
∂ ψ 4 D ∂ t a D = 1 η 4 D ∂ 2 ψ 4 D ∂ y D 2 ψ 4 D ( y D , 0 ) = 0 ψ 4 D ( y F D , t a D ) = ψ 2 D ∂ ψ 4 D ( y D , t a D ) ∂ y D y D = y e D = 0
3区基质控制方程：
∂ ψ 3 D ∂ t a D = 1 η 3 D ∂ 2 ψ 3 D ∂ y D 2 ψ 3 D ( y D , 0 ) = 0 ψ 3 D ( y F D , t a D ) = ψ 1 D ∂ ψ 3 D ( y D , t a D ) ∂ y D y D = y e D = 0
2区基质控制方程：
∂ 2 ψ 2 D ∂ x D 2 = 3 w 2 λ 12 ∂ ψ 2 D ∂ t a D - 6 λ 24 y F D ∂ ψ 4 D ∂ y D y = y F D ψ 2 D ( x D , 0 ) = 0 ψ 2 D ( d D 2 , t a D ) = ψ 1 D ∂ ψ 2 D ( x D , t a D ) ∂ x D x D = 1 = 0

1区缝网控制方程

∂ 2 ψ 1 D ∂ x D 2 - γ 1 D ( ∂ ψ 1 D ∂ x D ) 2 = 3 w 1 λ 1 F e γ 1 D ψ 1 D ∂ ψ 1 D ∂ t a D - 6 e γ 1 D ψ 1 D λ 13 y F D ∂ ψ 3 D ∂ y D y = y F D ψ 1 D ( x D , 0 ) = 0 ψ 1 D ( 0 , t a D ) = ψ F D ∂ ψ 1 D ( x D , t a D ) ∂ x D x D = d D 2 = e γ 1 D ψ 1 D d D 2 R C D ∂ ψ 2 D ( x D , t a D ) ∂ x D x D = d D 2
内区主裂缝控制方程：
∂ 2 ψ F D ∂ y D 2 = w F ∂ ψ F D ∂ t a D - λ 1 F e γ 1 D ψ 1 D 3 ∂ ψ 1 D ∂ x D x D = d D 2 ψ F D ( y D , 0 ) = 0 ψ F D ( 0 , t a D ) = 1 ∂ ψ F D ( y D , t a D ) ∂ t a D y D = y F D = 0

3 模型求解

考虑无因次渗流方程中拟渗透率模量项的强非线性为准确获取无因次拟压力解析解带来了较大的困难，因此引入Pedrosa变量对拟压力项替换处理以减轻渗流控制方程的非线性［25］，该变量表达式为：
ψ D = - 1 γ D L n ( 1 - γ D ⋅ ζ D )
式中： ζ D为摄动变换函数
将式（37）代入上述无因次渗流控制方程组，整理发现：由于基质区域不考虑应力敏感性的影响，因此 ψ i D = ζ i D ( i = 2,3 , 4 )。
对1区缝网无因次渗流控制方程化简整理可得：
∂ 2 ζ 1 ∂ x D 2 = 3 w 1 λ 1 F ⋅ ∂ ζ 1 ∂ t a - 6 λ 13 y F D ⋅ 1 1 - γ 1 D ζ 1 D ∂ ζ 3 ∂ y D
基于正则摄动理论，考虑到 1 1 - γ 1 D ζ 1 D项在缝网控制方程中的非线性，将该项泰勒展开得：
1 1 - γ 1 D ζ 1 D = 1 + γ 1 D ζ 1 D + ( γ 1 D ζ 1 D ) 2 + ( γ 1 D ζ 1 D ) 3 + . . . . . . .
由于无因次拟渗透率模量 γ 1 D ≪ 1，可认为 γ 1 D ζ 1 D项是一个小参数，因此零阶近似解已满足工程精度要求，即可仅取式（39）右端第一项，则1区无因次控制方程可化简为：
∂ 2 ζ 1 D ∂ x D 2 = 3 w 1 λ 1 F ⋅ ∂ ζ 1 D ∂ t a - 6 λ 13 y F D ∂ ζ 3 D ∂ y D
初边界条件依次简化为：
初始条件：
ζ 1 D ( x D , 0 ) = 0
外边界条件：
ζ 1 D ( 0 , t a D ) = ζ F D 1 - e - γ 1 D γ 1 D
内边界条件：
∂ ζ 1 D ( x D , t a D ) ∂ x D x D = d D 2 = d D 2 R C D ∂ ζ 2 D ( x D , t a D ) ∂ x D x D = d D 2
同样对主裂缝无因次控制方程组（36）依次采用Pedrosa变量替换、正则摄动法处理可以化简为：
∂ 2 ζ F D ∂ y D 2 = w F ∂ ζ F D ∂ t a D - λ 1 F 3 ∂ ζ 1 D ∂ x D x D = d D 2 ζ F D ( y D , 0 ) = 0 ζ F D ( 0 , t a D ) = 1 ∂ ζ F D ( y D , t a D ) ∂ t a D y D = y F D = 0
为便于求解模型，需要将上述中间变量替换处理过的无因次渗流控制方程组中的拟压力项依次进行Laplace变换：
ζ L D = L [ ζ D ] = ∫ 0 ∞ ζ D e - s t D d t D
首先对无因次4区渗流控制方程两端同时乘以 e - s t D，并对无因次时间进行从0到无穷大积分：
∫ 0 ∞ e - s t a D ∂ ζ 4 D ∂ t a D d t a D = 1 η 4 D ∫ 0 ∞ e - s t a D ∂ 2 ζ 4 D ∂ y D 2 d t a D
对式（46）等式左端化简：
∫ 0 ∞ e - s t a D ∂ ζ 4 D ∂ t a D d t a D = ∫ 0 ∞ e - s t a D d ζ 4 D = e - s t a D ζ 4 D 0 ∞ + s ∫ 0 ∞ e - s t a D ζ 4 D d t a D = s ζ L 4 D
对式（46）右端积分项化简：
∫ 0 ∞ e - s t a D ∂ 2 ζ 4 D ∂ y D 2 d t a D = ∂ 2 ∫ 0 ∞ e - s t a D ζ 4 D d t a D ∂ y D 2 = ∂ 2 ζ L 4 D ( y D , s ) ∂ y D 2
将式（47）和式（48）代入式（46）中得到Laplace空间内的外区基质无因次渗流方程：
∂ 2 ζ L 4 D ∂ y D 2 = s η 4 D ζ L 4 D
结合边界条件：
ζ L 4 D ( y F D , s ) = ζ L 2 D ∂ ζ L 4 D ( y D , s ) ∂ y D y D = y e D = 0
推导得到Laplace空间下的4区无因次拟压力解：
ζ L 4 D ( y D , s ) = ζ L 2 D c o s   h s η 4 D ( y e D - y D ) c o s   h s η 4 D ( y e D - y F D )
与4区Laplace空间下的无因次渗流方程推导过程类似拟压力推导过程类似，可依次求解3区基质、2区基质、1区缝网和主裂缝区域的拟压力项的Laplace形式：
Laplace空间下的3区基质无因次拟压力项解：
ζ L 3 D ( y D , s ) = ζ L 1 D c o s   h s η 3 D ( y e D - y D ) c o s   h s η 3 D ( y e D - y F D )
Laplace空间下的2区基质无因次拟压力项解：
ζ L 2 D ( x D , s ) = ζ L 1 D c o s   h ( α 2 ( 1 - x D ) ) c o s   h ( α 2 ( 1 - d D 2 ) )
式中：
α 2 = 3 w 2 s λ 12 + 6 s η 4 D λ 24 y F D t a n   h ( s η 4 D ( y e D - y F D ) )
Laplace空间下的1区缝网无因次拟压力项解：
ζ L 1 D ( x D , s ) = ζ L F 1 - e - γ 1 D γ 1 D c 3 s i n   h ( α 1 ( x D - d D 2 ) ) + c o s   h ( α 1 ( x D - d D 2 ) ) - c 3 s i n   h ( α 1 ( d D 2 ) ) + c o s   h ( α 1 d D 2 )
式中：
c 3 = λ 12 λ 1 F α 2 α 1 t a n   h ( α 2 ( d D 2 - 1 ) )
α 1 = 3 w 1 s λ 1 F + 6 s η 3 D λ 13 y F D t a n   h ( s η 3 D ( y e D - y F D ) )
Laplace空间下的主裂缝无因次拟压力项解：
ζ L F D ( y D , s ) = c o s   h ( α 4 ( y D - y F D ) ) c o s   h ( α 4 y F D )
其中：
α 4 = w F s - λ 1 F α 3 3 γ f D ( 1 - e - γ f D )
α 3 = α 1 c 3 c o s   h ( α 1 ( x D - d D 2 ) ) + α 1 s i n   h ( α 1 ( x D - d D 2 ) ) - c 3 s i n   h ( α 1 ( d D 2 ) ) + c o s   h ( α 1 d D 2 )
则Laplace空间内的矩形封闭外边界无因次定压产能解为：
q L D = - 1 2 π ∂ ζ L F D ∂ y D y D = 0 = α 4 2 π s t a n   h ( α 4 ⋅ y F D )
基于Stehfest数值反演得到实空间中的无因次产量半解析解，在此基础上，结合牛顿迭代方法，可获得定压生产时的实空间下的产量解。

4 模型验证与分析

4.1　实例计算及预测

以威远页岩气示范区某多级压裂水平井为例，其相关地质参数和水平井参数如表2所示，通过调整该模型的相关参数，本文提出的半解析模型对该井的生产动态数据进行了拟合。
表2 气藏地质参数和水平井参数

Table 2 Reservoir geological parameters and completion parameters

参数名称 取值 参数名称 取值
初始地层压力/MPa 45 压裂段数 25
地层温度/K 392.4 *裂缝半长/m 100
储层厚度/m 30 *主裂缝宽度/m 0.002
基质孔隙度 0.038 *外边界范围/m 300
基质渗透率/ ( 10 - 3   μ m 2 ) 0.000 247 水平井长度/m 1 500
缝网孔隙度 0.047 井底流压/MPa 5
缝网渗透率/ ( 10 - 3   μ m 2 ) 0.851 岩石密度/（kg/m3） 2 600
主裂缝渗透率/ ( 10 - 3   μ m 2 ) 750 缝网压敏系数/MPa-1 0.12
Langmuir体积/（m3/t） 2.5 Langmuir压力/MPa 8.5
储层初始压缩系数/MPa-1 8.78×10-4 压裂簇数/段 3
*主裂缝压裂带半宽/m 5

注： * 表示模型拟合参数

由图2可知，本文的产能模型曲线与生产数据曲线趋势基本一致，拟合效果良好；如图3所示，在气井投产1年前非线性效应对产量的贡献程度不明显，但非线性效应随着气井生产年限的增加对页岩气井产量的影响不可忽略，依据模型计算气井生产20年的累积产量为 1.35 × 10 8   m 3。当不考虑上述非线性因素之一时，产能模型预测的结果偏低。该产能半解析模型紧密联系现场压裂完井参数和生产数据，较符合现场生产实际的产能预测结果；产能模型中考虑的非线性越完善，计算精度也大幅提高，可合理评价预测气井中长期的产能大小和预测EUR值。
图2 模型验证结果

Fig.2 Model verification results

图3 模型预测结果

Fig.3 Model prediction results

4.2　产能影响因素分析

页岩气储层多级压裂水平井的累产气量与裂缝参数和水平井参数密切相关。本文基于该水平井产能预测模型，明确并优化气体产量的重要影响因素以最大限度地提高页岩气井EUR值。

4.2.1　裂缝参数

气井前期的生产规律受裂缝参数如主裂缝半长、主裂缝簇间距、主裂缝导流能力及次生裂缝压力敏感性等影响效果明显。

4.2.1.1　主裂缝半长

当其他参数一定，人工裂缝半长分别为50 m、75 m、100 m、125 m及150 m时，分析气井产量关于裂缝半长的变化趋势，并分别作出不同裂缝半长条件下压裂水平井产量典型曲线［图4（a）］和产气量关于裂缝半长的关系曲线［图4（b）］。
图4 不同主裂缝半长对页岩气产能的影响

Fig.4 Effect of different main fracture length on shale gas productivity

从图4（a）可知：当其他因素不变时，裂缝半长主要影响气井生产中前期的生产规律，裂缝半长越大，气井日产量随时间的递减曲线越平缓，首日产气量和累产气量随着裂缝半长的增加呈近似线性增长［图4（b）］，具体表现为裂缝半长从50 m增加到150 m时，气井初始日产气量和累产气量分别提高了 1.22 × 10 6   m 3 / d和 7.5 × 10 7   m 3。由此可见，裂缝半长值越大，水力压裂形成的缝网波及范围越广，储层气体动用程度越高，因此应尽可能造长缝。

4.2.1.2　主裂缝簇间距

当其他参数不变，设定主裂缝簇间距的值在5~60 m间变化的过程中分析主裂缝簇间距对产量的影响规律。
图5曲线结果表明：主裂缝簇间距对气井生产前期的生产规律影响明显，当簇间距取值在10~30 m间时，气井日产气量和累产气量随簇间距降低而明显增加，从理论上而言，降低簇间距意味着对储层重复压裂，增加了水平井上的主裂缝数量，进一步有效地沟通了致密储层的天然裂缝，气井的累产气量和最终采收率相应增加；但簇间距在5~10 m和30~60 m间变化时，气井的日产量和累产气量变化趋势减缓，储层动用差异不明显，这说明簇间距取值过高时储层改造效果较差、储层动用程度低，簇间距取值低至10 m左右时可认为储层改造程度足够充分，因此本文簇间距可优选10 m左右，20年的累产气量相对簇间距为20 m的气井累产气量可提高41%。
图5 不同主裂缝簇间距对页岩气产能的影响

Fig.5 Effect of different main fracture cluster spacing on shale gas productivity

4.2.1.3　主裂缝导流能力的影响

主裂缝导流能力是主裂缝渗透率与宽度的乘积，反映出裂缝向井筒传输气体的能力的高低。当保证其他参数不变时，改变主裂缝的渗透率，分别取值 0.75 × 10 - 12   m 2、 1.0 × 10 - 12   m 2、1.5×10-12 m2、 2.0 × 10 - 12   m 2和 4.0 × 10 - 12   m 2时，计算得到不同的主裂缝导流能力并分析对气井产量的影响规律。
图6表明，导流能力取值为 1.5 × 10 - 15   m 3增加到 4.0 × 10 - 15   m 3时，气井首日产气量和累产气量增长明显，首日产气量和累产气量分别增加了 5.15 × 10 5   m 3 / d和 9.4 × 10 7   m 3，日产气量递减幅度越低。这是因为裂缝导流能力增加，近井区域的气体流动阻耗降低，压力降漏斗剖面波及速度快，气体流动区域增大，产气量增加。当导流能力增至 1.5 × 10 - 15   m 3时，基质的渗透率远小于裂缝系统的渗透率，基质中气体的输运能力远不足以供应裂缝中气体的产出量，导致日产气量和累产气量增长幅度较为缓慢，因此实际压裂过程中时，本文裂缝导流能力应存在一个最优值约为 4.0 × 10 - 15   m 3，可以达到压裂效果最优化。
图6 不同主裂缝导流能力对页岩气产能的影响

Fig.6 Effect of different main fracture conductivity on shale gas productivity

4.2.1.4　次生缝网应力敏感性的影响

由于无支撑次生缝网易受到地层压力的变化发生裂缝闭合的现象，导致气体流动能力大幅度减弱，因此研究不同取值下的压敏系数对气井生产能力的影响规律，如图7所示。
图7 不同压敏系数对页岩气产能的影响

Fig.7 Effect of different fracture network stress sensitivity on shale gas productivity

从图7可以看出：日产气量和累产气量与应力敏感性系数呈线性递减关系，当应力敏感性系数越高，气井日产气量和累产气量越小，说明次生缝网有效应力的改变对渗透率变化影响较大，地层有效应力降低导致裂缝逐渐发生部分闭合等现象，气体流动能力明显减弱，气体向井筒汇聚的累产气量越少，因此在水力压裂过程中应优选强度较高、耐压性好的陶粒支撑剂以减少缝网渗透率的损失，或者在水力压裂的过程中设计剪切应力造成裂缝面滑移以增加裂缝面粗糙度和开度。

4.2.2　水平井巷道间距

研究表明［26］，确定合适的巷道间距范围是实现页岩储层资源充分动用，降低资源浪费风险的前提，因此本文研究了巷道间距对气井产量的影响规律，明确了产能取最优值时巷道间距的理论最佳范围。当储层参数和工程参数不变时，水平井巷道间距分别取200 m、300 m、400 m、500 m时，分别得到了气井产量随时间变化曲线以及产气量和巷道间距的关系曲线（图8）。
图8 不同水平井巷道间距对页岩气产能的影响

Fig.8 Effect of different horizontal well spacing on shale gas productivity

如图8所示，首日日产气量和累产气量随着巷道间距增加而呈线性增大，巷道间距为500 m的气井投产20年的首日产气量和累产气量相比巷道间距为200 m的值分别提高了将近一倍和35%，这是由于巷道间距增加时，单井控制的地层储量也增大，气体动用程度较高。因此本文建议水平井巷道间距优选值约为500 m。

4.2.3　水平段长度

目前国内外水平井开发技术已经比较成熟，大部分水平段长度范围为1 500~2 000 m。为提高气井经济开发效益，当其他模型参数不变时，本文分析了不同水平段长度对气井产能的影响规律。
图9（a）研究结果表明，随着水平段长的增加，气井递减率降低，累产气量相应增加。从图9（b）看出水平段长度为3 000 m的累产气量相比长度为1 500 m的气井产气量增加了将近一倍。综上所述，水平井长度的增加极大程度增加了储层的泄气面积，储层动用程度明显提高，在综合考虑复杂地质特征和现场施工难度的前提下建议在局部地区可适量部署长度为2 000~3 000 m的水平井进行技术攻关。
图9 不同水平段长度对页岩气产能的影响

Fig.9 Effect of different horizontal well length on shale gas productivity

5 结论

（1）基于常规五区复合渗流模型，在基质方程中采用了过剩量修正的超临界吸附模型并将其耦合到基质解吸系数中，并引入了考虑储层低压下的扩散、滑脱的表观渗透率模型，在缝网控制方程中运用指数形式的应力敏感性模型表征应力敏感性对气体在缝网流动能力的影响，并综合分析了气体在采出过程中高压物性参数变化对产量的影响，建立了改进的五区复合渗流模型。
（2）主要采用Laplace变换、Stehfest数值反演和牛顿迭代方法推导得到气井实空间的产能半解析解，通过实例生产数据的历史拟合验证了该产能模型的可行性；由模型预测曲线发现：非线性效应对产量的贡献程度随着生产年限的延长而增加，预测20年气井EUR值为 1.35 × 10 8   m 3。当不考虑非线性因素之一时，产能模型预测的结果明显偏低。该产能半解析模型紧密联系现场压裂完井参数和生产数据，考虑的非线性效应越完善，产能计算精度也越高，可合理评价预测气井中长期的产能大小和预测EUR值。
（3）分别从裂缝参数和水平井参数对气井产能进行了单因素敏感性分析，结果表明：①裂缝半长越大，产能越大，因此应尽可能造长缝；②主裂缝簇间距和主裂缝导流能力值取一定范围时，产气量和两者值呈正相关，但是两者值过高或者过低时，储层动用程度变化不明显，本文主裂缝簇间距和导流能力取值可分别优选在10 m附近 和4.0×10-15 m3左右；应力敏感系数越大，产能越低，压裂过程应优选性能优良的支撑剂或设计剪切应力造成裂缝面滑移以提高裂缝导流能力；③水平井巷道间距越大，产能越高，在实际生产中巷道间距可优选500 m左右，20年累产气量相对300 m的累产气量可提高30%；水平段越长，产能越高，长度3 000 m的水平井的20年可采储量相对1500 m的水平井的累产气量可提高将近一倍。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
1
贾爱林，位云生，金亦秋.中国海相页岩气开发评价关键技术进展［J］.石油勘探与开发， 2016， 43（6）： 949-955.

JIA A L， WEI Y S， JIN Y Q. Key technical progress of marine shale gas development evaluation in China ［J］. Petroleum Exploration and Development， 2016， 43（6）： 949-955.

2
端祥刚，胡志明， 高树生，等.页岩高压等温吸附曲线及气井生产动态特征实验［J］.石油勘探与开发，2018， 45（1）：119-127.

DUAN X G， HU Z M， GAO S S， et al. Experiment of shale high-pressure isothermal adsorption curve and gas well production performance characteristics［J］. Petroleum Exploration and Development， 2018， 45（1）：119-127.

3
郭为，胡志明， 熊伟， 等.页岩等温吸附曲线SLD_PR模拟方法及应用［J］.石油勘探与开发，2015， 36（1）： 162-167.

GUO W，HU Z M，XIONG W， et al. Shale isothermal adsorption curve SLD_PR simulation method and application［J］. Petroleum Exploration and Development，2015，36（1）： 162-167.

4
熊健，梁利喜， 刘向君， 等.基于吸附势理论的页岩对甲烷吸附特性［J］.科技导报，2014， 32（14）：19-22.

XIONG J， LIANG L X， LIU X J， et al. Methane adsorption characteristics of shale based on adsorption potential theory［J］.Science and Technology Herald，2014， 32（14）：19-22.

5
熊伟， 左罗，郭为，等.页岩气赋存力学机制［J］.新疆石油地质，2014， 35（2）：158-162.

XIONG W， ZUO L， GUO W， et al. Mechanical mechanism of shale gas occurrence［J］.Xinjiang Petroleum Geology，2014， 35（2）：158-162.

6
宁正福， 王庆， 张睿，等.吸附势理论的页岩气藏吸附平衡预测［J］.新疆石油地质，2015， 36（3）：308-312.

NING Z F， WANG Q， ZHANG R， et al. Adsorption equilibrium prediction of shale gas reservoirs based on adsorption potential theory［J］. Xinjiang Petroleum Geology， 2015， 36（3）：308-312.

7
孔德涛， 宁正福， 杨峰， 等. 页岩气吸附规律研究［J］. 科学技术与工程， 2014， 14（6）： 108-111.

KONG D T， NING Z F， YANG F， et al. Study on the shale gas adsorption rule［J］. Science Technology and Engineering， 2014， 14（6）： 108-111.

8
BESKOK A L I， KARNIADAKIS GEORGE. A model for flows in channels， pipes， and ducts at micro and nanoscales［J］. Microscale Thermophysical Engineering， 1999， 3（1）： 43-77.

9
CIVAN F. Effective correlation of apparent gas permeability in tight porous media［J］. Transport in Porous Media， 2010， 82（2）： 375-384.

10
JAVADPOUR F. Nanopores and Apparent Permeability of Gas Flow in Mudrocks （Shales and Siltstone） ［J］. Journal of Canadian Petroleum Technology， 2009， 48（8）： 16-21.

11
吴克柳， 李相方， 陈掌星.页岩气纳米孔气体传输模型［J］.石油学报， 2015， 36（7）：837-848.

WU K L， LI X F， CHEN Z X.Shale gas nanopore gas transport model［J］.Acta Petrolei Sinica， 2015， 36（7）：837-848.

12
El B. Analysis of Tight Gas Wells［D］. Texas：College Station， Texas A＆M U， 1998.

13
AHMADI H A， ALMARZOOQ A， WATTENBARGER R. Application of linear flow analysis to shale gas wells-field cases［C］//SPE Unconventional Gas Conference. Pittsburgh， 2010.

14
BROWN M，OZKAN E，RAGHAVAN R，et al. Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs［C］.SPE 125043，2009.

15
BROWN M，OZKAN E， RAGHAVAN R， et al. Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs［J］. SPE Reservoir Evaluation Eng， 2011， 14： 663-676

16
郭小哲， 周长沙.页岩气储层压裂水平井三线性渗流模型研究［J］.西南石油大学学报：自然科学版，2016，38（2）：86-94.

GUO X Z， ZHOU C S. The trilinear seepage model for fractured horizontal well in shale gas reservior［J］.Journal of Southwest Petroleum University：Science & Technology Edition，2016，38（2）：86-94.

17
吴永辉， 程林松， 黄世军， 等.考虑页岩气赋存及非线性流动机理的产能预测半解析方法［J］. 中国科学：技术科学， 2018， 48（6）：691-700.

WU Y H， CHENG L S， HUANG S J， et al. A semi-analytical method for productivity prediction considering shale gas occurrence and nonlinear flow mechanism［J］. Science in China： Technology Science， 2018， 48（6）：691-700.

18
STALGOROVA K， MATTAR L. Analytical model for unconventional multifractured composite systems［J］. SPE Reservoir Evaluation Eng， 2013， 16： 246-256.

19
尹洪军，赵二猛，付京，等. 页岩气藏压裂水平井五区复合模型产能分析［J］.西南石油大学学报：自然科学版，2015，37（3）：9-16.

YIN H J， ZHAO E M， FU J， et al. Production analysis of composite model of five regions for fractured horizontal wells in shale gas reservoirs［J］.Journal of Southwest Petroleum University： Science & Technology Edition， 2015， 37（3）：9-16.

20
ANDERSON D M， NOBAKHT M， MOGHADAM S，et al.Analysis of production data from fractured shale gas wells［C］//SPE Unconventional Gas Conference，Society of Petroleum Engineers，2010.

21
GERAMI S， DARVISH M. POOLADI， MORAD K，et al. Type curves for dry CBM reservoirs with equilibrium desorption［C］. Petroleum Society of Canada Canadian International Petroleum Conference - Calgary， Alberta （2007-06-12）.

22
艾爽，程林松，黄世军，等，页岩气体积压裂水平井非稳态产能评价模型［J］.天然气地球科学，2014，25（10）：1661-1667.

AI S， CHENG L S， HUANG S J， et al.Transient production for forcasdting model of multiply fractured horizontal wells in shale gas reservoirs［J］.Natural Gas Geoscience，2014，25（10）：1661-1667.

23
PERROSA O A. Pressure transient response in stress-sensitive formation［C］. SPE 15115， presented at SPE California Regional Meeting held in Oakland， California， 1986，April 2-4，

24
KAZEMI H， SETH M S， THOMAS G W. The interpretation of interference tests in naturally fractured reservoirs with uniform fracture distribution［J］.SPE Journal，1969，9：463-472.

25
郭平.低渗透致密砂岩气藏开发机理研究［M］.北京：石油工业出版社，2009.

GUO P. Research on Development Mechanism of Low Permeability Tight Sandstone Gas Reservoir［M］.Beijing：Petroleum

Industry Press，2009.

26
杨洪志， 张小涛， 陈满， 等.四川盆地长宁区块页岩气水平井地质目标关键技术参数优化［J］. 天然气工业， 2016， 36（6）： 60-65.

YANG H Z， ZHANG X T， CHEN M， et al. Optimization of key technical parameters for geological targets of shale gas horizontal wells in the Changning Block， Sichuan Basin［J］. Natural Gas Industry， 2016， 36（6）： 60-65.

Options
文章导航

/

〈 〉

陇ICP备2021001824号-7　 甘公网安备 62010202000678号
版权所有 © 《天然气地球科学》编辑部
地址：甘肃省兰州市天水中路8号　
邮编：730000　
电话：(0931)8277790　
E-mail：geogas@lzb.ac.cn
总访问量 　 今日访问 　 在线人数
技术支持：北京玛格泰克科技发展有限公司