0 引言
1 模型建立
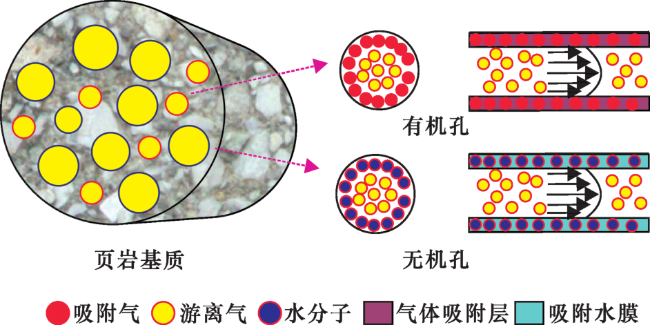
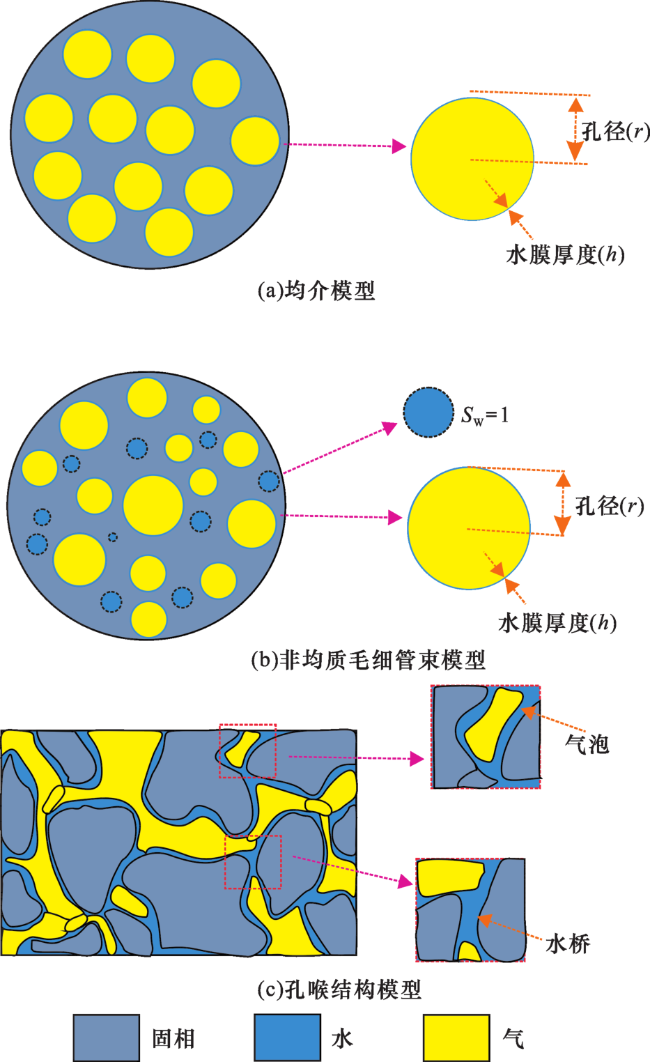
1.1 物理模型
1.2 有机质孔隙表观渗透率模型
1.2.1 有机质有效孔隙半径
1.2.2 表面扩散
1.2.3 自由气传输模型
1.2.4 有机质表观渗透率
1.3 无机质孔隙表观渗透率模型
1.4 页岩基质表观渗透率模型
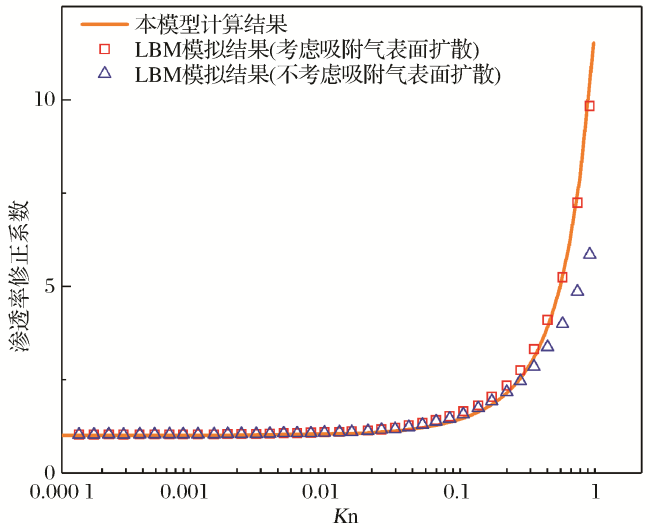
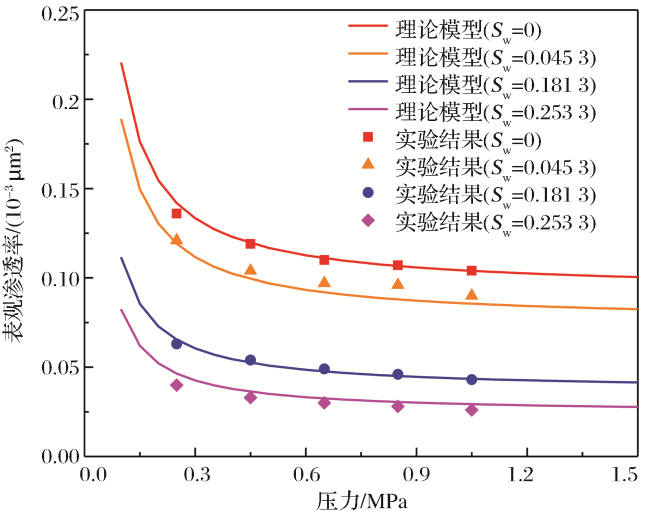
2 模型验证
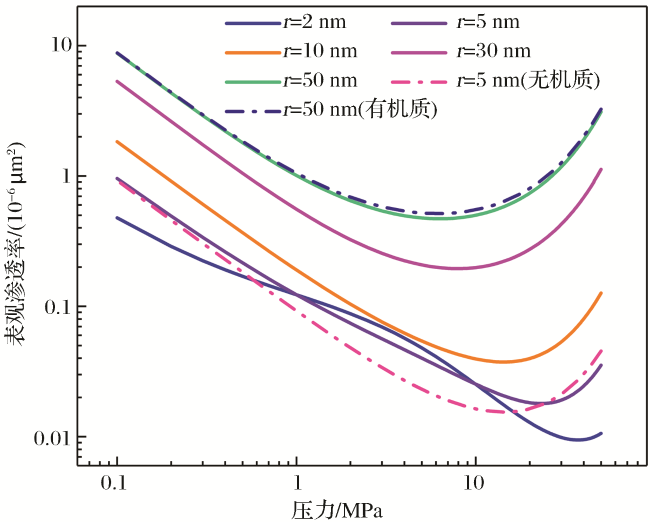
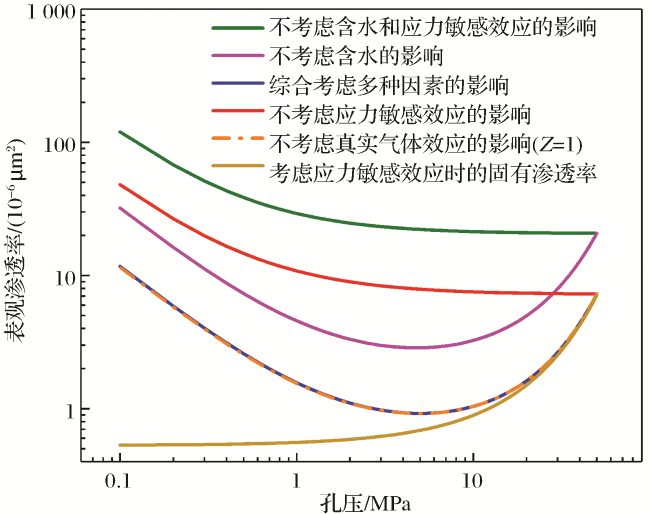
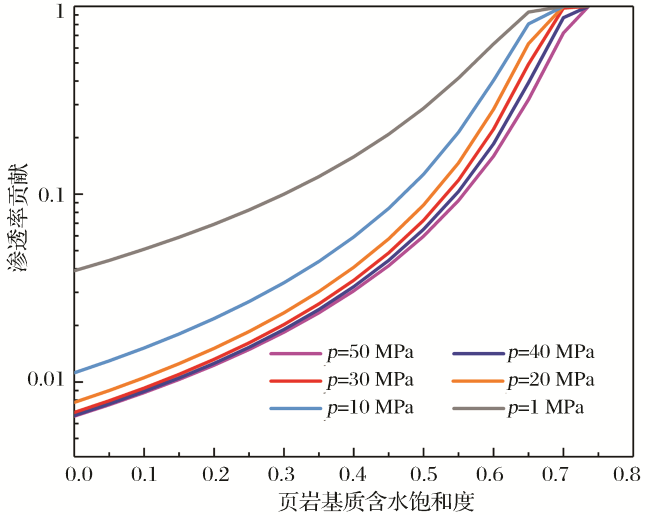
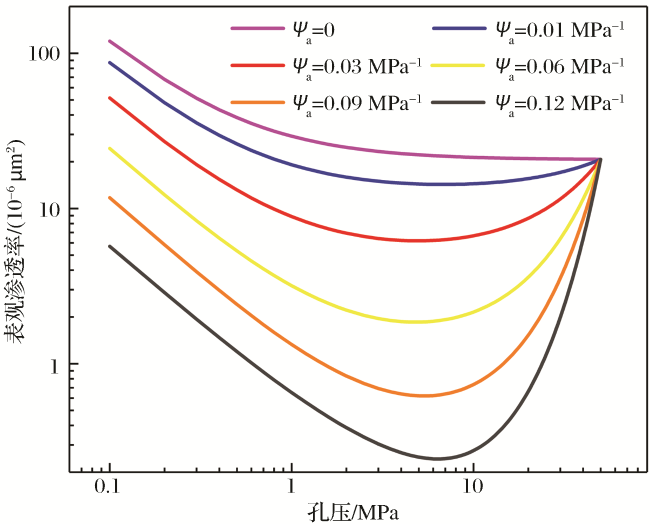
3 敏感性参数分析
表1 页岩岩石物性和气体特性参数Table 1 Physical properties and gas characteristics parameter of shale |
| 参数 | 取值 | 参数 | 取值 |
|---|---|---|---|
| 等效有机质孔径(r 0-or)/ nm | 10.2 | 等效无机质孔径(r 0-iom)/nm | 75.94 |
| 有机质孔隙度(Ф or) | 0.018 | 无机质孔隙度(Ф iom) | 0.05 |
| 温度(T)/K | 353 | 理想气体黏度(μ g0)/(mPa·s) | 1.49×10-2 |
| 孔隙压力(P)/MPa | 0.1~50 | 上覆地层压力(P c)/MPa | 50 |
| Langmuir压力(P L)/MPa | 13.7 | Langmuir体积(V L)/(m3/m3) | 10 |
| 最大气体浓度(C max)/(mol/m3) | 328.7 | 有机质含量(ψ t)/% | 0.05 |
| 孔隙度应力敏感系数(C a)/ MPa-1 | 0.002 | 渗透率应力敏感系数(C p)/MPa-1 | 0.048 |
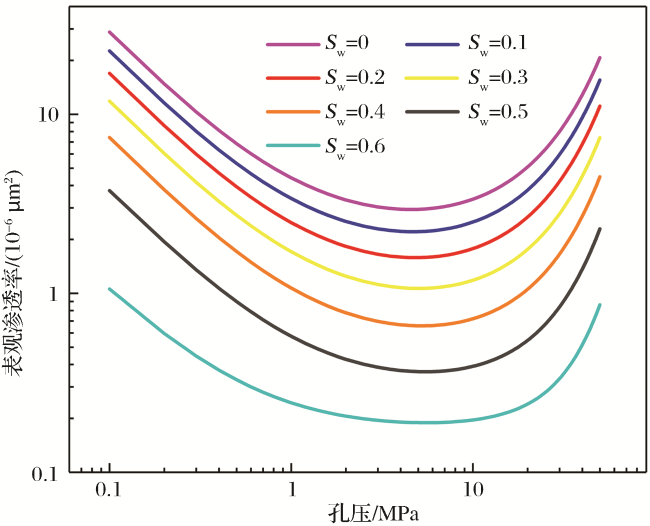
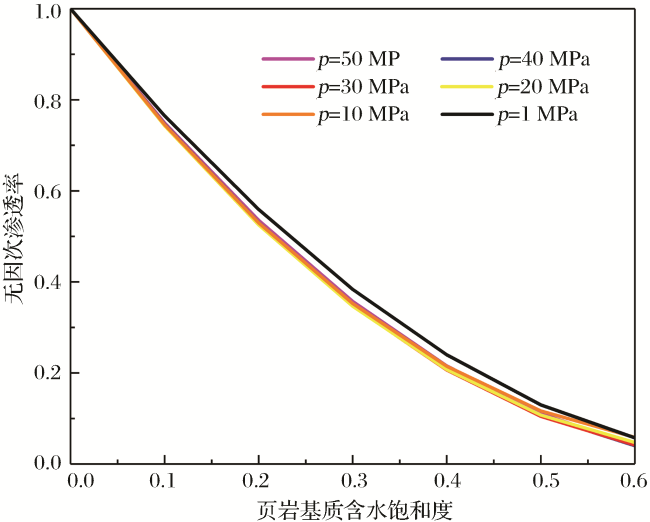
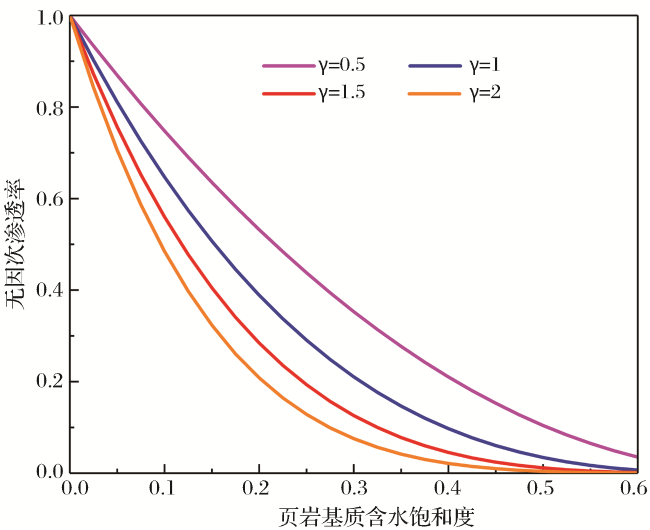
| 束缚水饱和度(Sw) | 0.15~0.6 | 吸附气密度(ρ a)/(kg/m3) | 394.1 |



 甘公网安备 62010202000678号
甘公网安备 62010202000678号