0 引言
1 气体渗流数学模型
1.1 气体渗流综合微分方程
1.2 气井定产量生产解
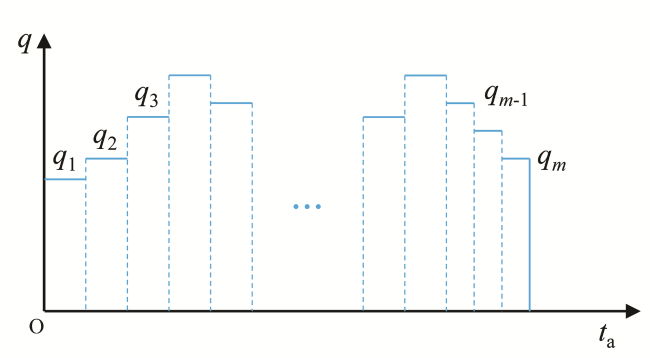
1.3 气井变产量生产解
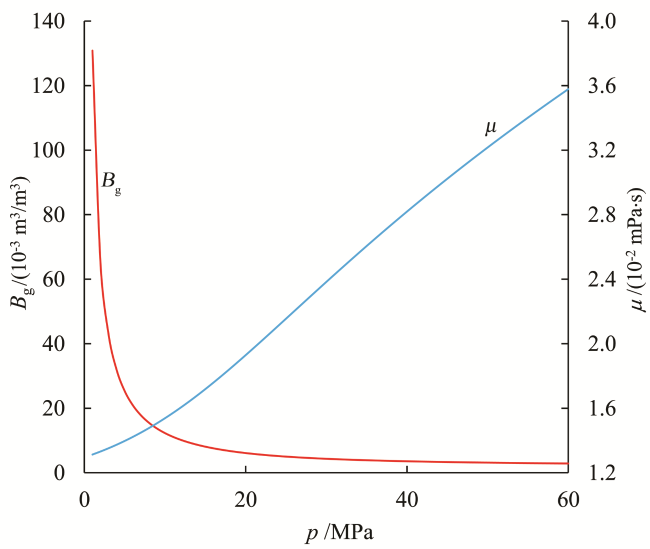
2 异常高压气藏物质平衡方程
3 异常高压气藏变产量探边测试法
4 数值模拟验证
表 1 气藏性质参数Table 1 Reservoir properties |
| 物理量 | 数值 |
|---|---|
| G /m3 | 1.519 063 10×108 |
| ϕ i | 0.2 |
| K/(10-3 μm2) | 3.0 |
| S wci | 0.2 |
| r e /m | 300 |
| r w /m | 0.1 |
| h /m | 10 |
| p i /MPa | 55 |
| T i /K | 381.15 |
| T pc /K | 201.325 729 |
| p pc /MPa | 4.597 109 |
| M g /(g/mol) | 19.576 754 |
| Z sc | 0.997 514 |
| μ i /mPa∙s | 3.401 434 212×10-2 |
| Cϕ /MPa-1 | 2.364×10-3 |
| C w /MPa-1 | 4.230×10-4 |
| μ w /mPa∙s | 0.264 565(at p i) |
| C gi /MPa-1 | 8.924 326 991×10-3 |
| C ti /MPa-1 | 9.588 061 593×10-3 |
| B gi /(m3/m3) | 2.980 066 777×10-3 |
| V pi /m3 | 565 864 |
4.1 定产量模拟
表2 定产量生产计划Table 2 Production schedules for the constant rate case |
| t /d | TS | Δt /h | Δt /d | q /(104 m3/d) |
|---|---|---|---|---|
| 1~1 097 | 1~12 | 1 | 0.041 667 | 1.6 |
| 13 | 3 | 0.125 | 1.6 | |
| 14 | 9 | 0.375 | 1.6 | |
| 15~16 | 12 | 0.5 | 1.6 | |
| 17~1 111 | 24 | 1 | 1.6 |
|
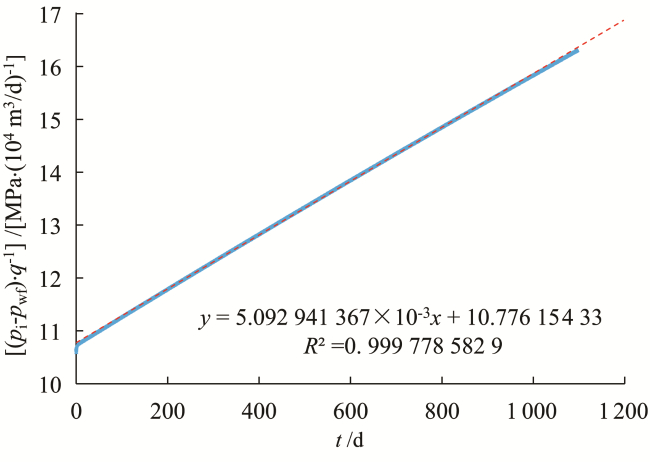
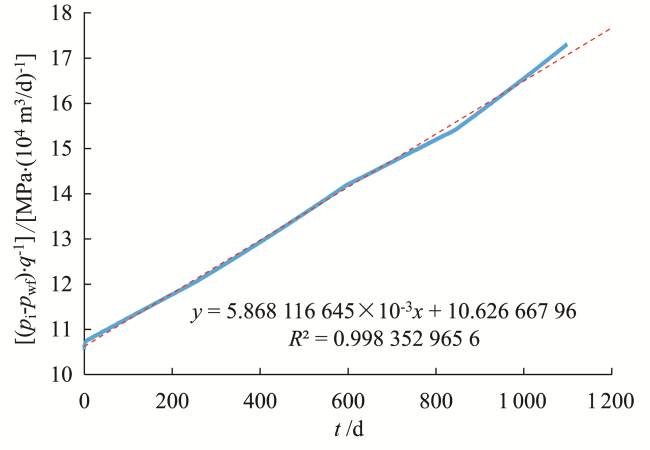
图3 定产条件下利用真实压力和真实时间得到的(p i-p wf)∙q -1—t关系曲线Fig.3 (p i-p wf)∙q -1 vs t from real pressure (p) and real time (t) data for the constant-flowrate case |
表3 定产条件下VRRLT-APGR方法的计算结果(初值储量G a=1.638 288 93×108 m3)Table 3 Estimation of gas in place using VRRLT-APGR method with an initial G a=1.638 288 93×108 m3 for the constant-flowrate case |
| No. | G a /m3 | m bdf /[10-3 MPa·(104 m3)-1] | G e /m3 | E a /% |
|---|---|---|---|---|
| 1 | 163 828 893 | 5.319 073 355 | 156 863 966 | 3.264 |
| 2 | 156 863 966 | 5.330 482 813 | 156 528 212 | 3.043 |
| 3 | 156 528 212 | 5.331 061 039 | 156 511 234 | 3.031 |
| 4 | 156 511 234 | 5.331 090 352 | 156 510 374 | 3.031 |
| 5 | 156 510 374 | 5.331 091 835 | 156 510 330 | 3.031 |
| 6 | 156 510 330 | 5.331 091 913 | 156 510 328 | 3.031 |
| 7 | 156 510 328 | 5.331 091 916 | 156 510 328 | 3.031 |
表4 定产条件下VRRLT-APGR方法的计算结果(初值储量G a=0.5×108 m3)Table 4 Estimation of gas in place using VRRLT-APGR method with an initial G a=0.5×108 m3 for the constant-flowrate case |
| No. | G a /m3 | m bdf /[10-3 MPa·(104 m3)-1] | G e /m3 | E a /% |
|---|---|---|---|---|
| 1 | 50 000 000 | 6.028 144 607 | 138 412 563 | -8.883 |
| 2 | 138 412 563 | 5.366 887 206 | 155 466 458 | 2.344 |
| 3 | 155 466 458 | 5.332 907 651 | 156 457 040 | 2.996 |
| 4 | 156 457 040 | 5.331 183 960 | 156 507 626 | 3.029 |
| 5 | 156 507 626 | 5.331 096 581 | 156 510 191 | 3.031 |
| 6 | 156 510 191 | 5.331 092 152 | 156 510 321 | 3.031 |
| 7 | 156 510 321 | 5.331 091 928 | 156 510 328 | 3.031 |
| 8 | 156 510 328 | 5.331 091 916 | 156 510 328 | 3.031 |
表5 定产条件下VRRLT-APGR方法的计算结果(初值储量G a=3.0×108 m3)Table 5 Estimation of gas in place using VRRLT-APGR method with an initial G a=3.0×108 m3 for the constant-flowrate case |
| No. | G a /m3 | m bdf /[10-3 MPa·(104 m3)-1] | G e /m3 | E a /% |
|---|---|---|---|---|
| 1 | 300 000 000 | 5.207 959 913 | 160 210 708 | 5.467 |
| 2 | 160 210 708 | 5.324 864 505 | 156 693 366 | 3.151 |
| 3 | 156 693 366 | 5.330 776 277 | 156 519 595 | 3.037 |
| 4 | 156 519 595 | 5.331 075 915 | 156 510 798 | 3.031 |
| 5 | 156 510 798 | 5.331 091 104 | 156 510 352 | 3.031 |
| 6 | 156 510 352 | 5.331 091 873 | 156 510 329 | 3.031 |
| 7 | 156 510 329 | 5.331 091 915 | 156 510 328 | 3.031 |
| 8 | 156 510 328 | 5.331 091 916 | 156 510 328 | 3.031 |
4.2 定压力模拟
表6 定流压生产计划Table 6 Production schedules for the constant pressure case |
| t /d | TS | Δt /h | Δt /d | p wf /MPa |
|---|---|---|---|---|
| 1~1 097 | 1~12 | 1 | 0.041 667 | 30 |
| 13 | 3 | 0.125 | 30 | |
| 14 | 9 | 0.375 | 30 | |
| 15~16 | 12 | 0.5 | 30 | |
| 17~1 111 | 24 | 1 | 30 |
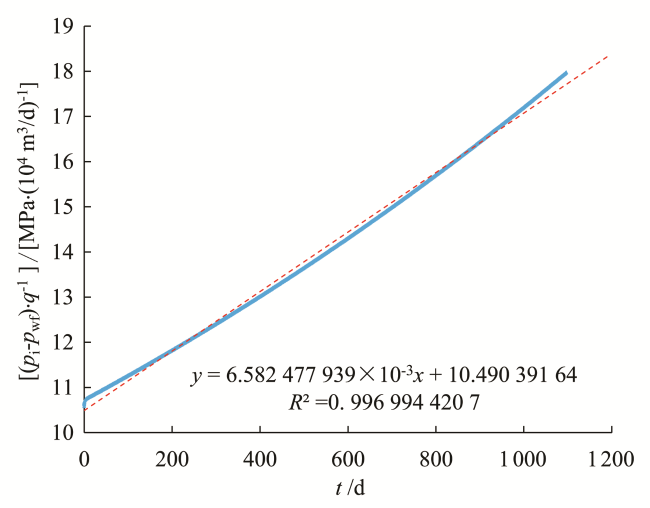
图4 定流压条件下(p i-p wf)∙q -1-t关系曲线Fig.4 (p i-p wf)∙q -1 vs t for the constant-pressure case |
表7 定压条件下VRRLT-APGR方法的计算结果(初值储量G a=1.267 563 60×108 m3)Table 7 Estimation of gas in place using VRRLT-APGR method with an initial G a=1.267 563 60×108 m3 for the constant bottomhole pressure case |
| No. | G a /m3 | m bdf /[10-3 MPa·(104 m3)-1] | G e /m3 | E a /% |
|---|---|---|---|---|
| 1 | 126 756 360 | 5.471 803 037 | 152 485 559 | 0.381 |
| 2 | 152 485 559 | 5.402 575 084 | 154 439 491 | 1.668 |
| 3 | 154 439 491 | 5.398 366 775 | 154 559 884 | 1.747 |
| 4 | 154 559 884 | 5.398 111 359 | 154 567 197 | 1.752 |
| 5 | 154 567 197 | 5.398 095 859 | 154 567 641 | 1.752 |
| 6 | 154 567 641 | 5.398 094 917 | 154 567 668 | 1.752 |
| 7 | 154 567 668 | 5.398 094 859 | 154 567 670 | 1.752 |
| 8 | 154 567 670 | 5.398 094 854 | 154 567 670 | 1.752 |
表8 定压条件下VRRLT-APGR方法的计算结果(初值储量G a=0.5×108 m3)Table 8 Estimation of gas in place using VRRLT-APGR method with an initial G a=0.5×108 m3 for the constant bottomhole pressure case |
| No. | G a /m3 | m bdf /[10-3 MPa·(104 m3)-1] | G e /m3 | E a /% |
|---|---|---|---|---|
| 1 | 50 000 000 | 6.170 943 023 | 135 209 633 | -10.991 |
| 2 | 135 209 633 | 5.445 776 149 | 153 214 330 | 0.861 |
| 3 | 153 214 330 | 5.400 991 467 | 154 484 774 | 1.697 |
| 4 | 154 484 774 | 5.398 270 652 | 154 562 636 | 1.749 |
| 5 | 154 562 636 | 5.398 105 525 | 154 567 364 | 1.752 |
| 6 | 154 567 364 | 5.398 095 504 | 154 567 651 | 1.752 |
| 7 | 154 567 651 | 5.398 094 896 | 154 567 669 | 1.752 |
| 8 | 154 567 669 | 5.398 094 856 | 154 567 670 | 1.752 |
表9 定压条件下VRRLT-APGR方法的计算结果(初值储量G a=3.0×108 m3)Table 9 Estimation of gas in place using VRRLT-APGR method with an initial G a=3.0×108 m3 for the constant bottomhole pressure case |
| No. | G a /m3 | m bdf /[10-3 MPa·(104 m3)-1] | G e /m3 | E a /% |
|---|---|---|---|---|
| 1 | 300 000 000 | 5.248 146 508 | 158 983 927 | 4.659 |
| 2 | 158 983 927 | 5.389 024 182 | 154 827 834 | 1.923 |
| 3 | 154 827 834 | 5.397 544 488 | 154 583 431 | 1.762 |
| 4 | 154 583 431 | 5.398 061 456 | 154 568 626 | 1.753 |
| 5 | 154 568 626 | 5.398 092 829 | 154 567 728 | 1.752 |
| 6 | 154 567 728 | 5.398 094 731 | 154 567 673 | 1.752 |
| 7 | 154 567 673 | 5.398 094 849 | 154 567 670 | 1.752 |
| 8 | 154 567 670 | 5.398 094 854 | 154 567 670 | 1.752 |
4.3 复杂生产计划模拟
表10 复杂生产制度Table 10 Complex production schedules |
| t /d | TS | Δt /h | Δt /d | Production Scenarios |
|---|---|---|---|---|
| 1~251 | 1~12 | 1 | 0.041 667 | q=2.0×104 m3/d |
| 13 | 3 | 0.125 | ||
| 14 | 9 | 0.375 | ||
| 15~16 | 12 | 0.5 | ||
| 17~265 | 24 | 1 | ||
| 252~592 | 266~606 | 24 | 1 | p wf=30.9 MPa |
| 593~842 | 607~856 | 24 | 1 | q=1.7×104 m3/d |
| 843~1 097 | 857-1 111 | 24 | 1 | p wf=28.8 MPa |
图5 复杂生产条件下(p i-p wf)∙q -1—t关系曲线Fig.5 (p i⁃p wf)∙q -1 vs t for the complex production schedules |
表11 VRRLT-APGR方法对于复杂生产制度的计算结果(初值储量G a=1.421 871 78×108 m3)Table 11 Estimation of gas in place using VRRLT-APGR method with an initial G a=1.421 871 78×108 m3 for the complex production schedules |
| No. | G a /m3 | m bdf /[10-3 MPa·(104 m3)-1] | G e /m3 | E a /% |
|---|---|---|---|---|
| 1 | 142 187 178 | 5.374 261 526 | 155 253 134 | 2.203 |
| 2 | 155 253 134 | 5.345 003 996 | 156 102 960 | 2.763 |
| 3 | 156 102 960 | 5.343 289 466 | 156 153 049 | 2.796 |
| 4 | 156 153 049 | 5.343 189 059 | 156 155 984 | 2.798 |
| 5 | 156 155 984 | 5.343 183 178 | 156 156 156 | 2.798 |
| 6 | 156 156 156 | 5.343 182 833 | 156 156 166 | 2.798 |
| 7 | 156 156 166 | 5.343 182 813 | 156 156 166 | 2.798 |
表12 VRRLT-APGR方法对于复杂生产制度的计算结果(初值储量G a=0.5×108 m3)Table 12 Estimation of gas in place using VRRLT-APGR method with an initial G a=0.5×108 m3 for the complex production schedules |
| No. | G a /m3 | m bdf /[10-3 MPa·(104 m3)-1] | G e /m3 | E a /% |
|---|---|---|---|---|
| 1 | 50 000 000 | 6.158 017 103 | 135 493 444 | -10.805 |
| 2 | 135 493 444 | 5.391 715 204 | 154 750 559 | 1.872 |
| 3 | 154 750 559 | 5.346 027 805 | 156 073 065 | 2.743 |
| 4 | 156 073 065 | 5.343 349 427 | 156 151 297 | 2.794 |
| 5 | 156 151 297 | 5.343 192 570 | 156 155 881 | 2.797 |
| 6 | 156 155 881 | 5.343 183 385 | 156 156 150 | 2.798 |
| 7 | 156 156 150 | 5.343 182 845 | 156 156 165 | 2.798 |
| 8 | 156 156 165 | 5.343 182 815 | 156 156 166 | 2.798 |
表13 VRRLT-APGR方法对于复杂生产制度的计算结果(初值储量G a=3.0×108 m3)Table 13 Estimation of gas in place using VRRLT-APGR method with an initial G a=3.0×108 m3 for the complex production schedules |
| No. | G a /m3 | m bdf /[10-3 MPa·(104 m3)-1] | G e /m3 | E a /% |
|---|---|---|---|---|
| 1 | 300 000 000 | 5.201 154 112 | 160 420 346 | 5.605 |
| 2 | 160 420 346 | 5.334 890 197 | 156 398 897 | 2.957 |
| 3 | 156 398 897 | 5.342 697 274 | 156 170 358 | 2.807 |
| 4 | 156 170 358 | 5.343 154 378 | 156 156 997 | 2.798 |
| 5 | 156 156 997 | 5.343 181 149 | 156 156 215 | 2.798 |
| 6 | 156 156 215 | 5.343 182 715 | 156 156 169 | 2.798 |
| 7 | 156 156 169 | 5.343 182 807 | 156 156 166 | 2.798 |
| 8 | 156 156 166 | 5.343 182 813 | 156 156 166 | 2.798 |
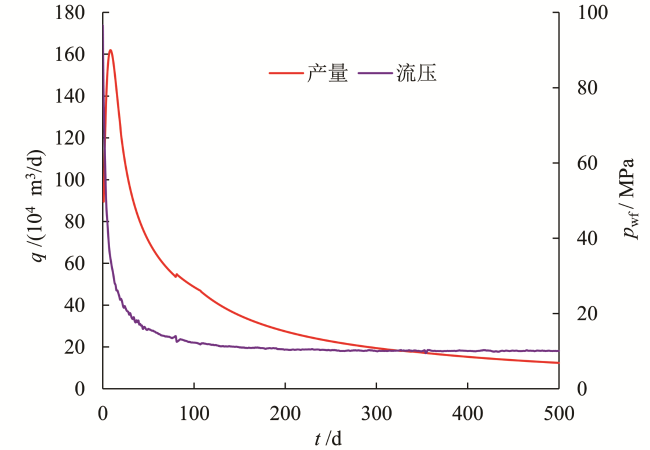
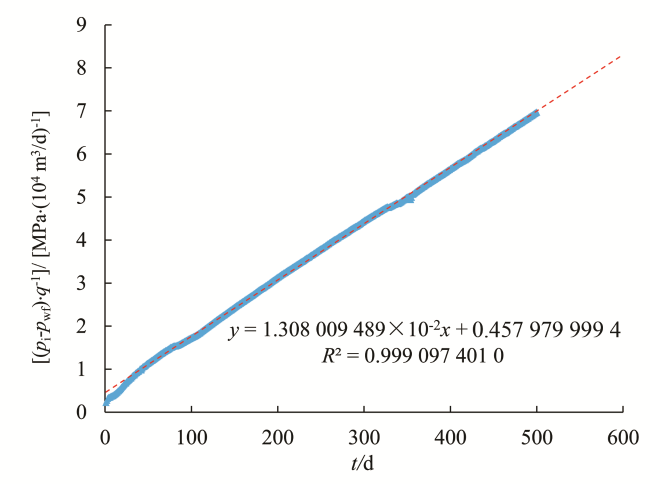
5 现场实例验证
5.1 实例1
表14 VRRLT-APGR方法对于现场实例1的计算结果(初值储量G a=46.06×108 m3)Table 14 Estimation of gas in place using VRRLT-APGR method with an initial G a=46.06×108 m3 for field case 1 |
| No. | G a /(108 m3) | m bdf /[10-4 MPa·(104 m3)-1] | G e /(108 m3) | E e /% |
|---|---|---|---|---|
| 1 | 46.062 240 820 | 1.246 314 231 | 43.738 295 917 | -5.045 |
| 2 | 43.738 295 917 | 1.246 546 239 | 43.730 155 317 | -0.019 |
| 3 | 43.730 155 317 | 1.246 547 093 | 43.730 125 358 | 0.000 |
| 4 | 43.730 125 358 | 1.246 547 098 | 43.730 125 182 | 0.000 |
表15 VRRLT-APGR方法对于现场实例1的计算结果(初值储量G a=20×108 m3)Table 15 Estimation of gas in place using VRRLT-APGR method with an initial G a=20×108 m3 for field case 1 |
| No. | G a /(108 m3) | m bdf /[10-4 MPa·(104 m3)-1] | G e /(108 m3) | E e /% |
|---|---|---|---|---|
| 1 | 20 | 1.252 039 704 | 43.538 284 343 | 117.691 |
| 2 | 43.538 284 343 | 1.246 567 369 | 43.729 414 067 | 0.439 |
| 3 | 43.729 414 067 | 1.246 547 173 | 43.730 122 551 | 0.002 |
| 4 | 43.730 122 551 | 1.246 547 098 | 43.730 125 182 | 0.000 |
| 5 | 43.730 125 182 | 1.246 547 098 | 43.730 125 182 | 0.000 |
表16 VRRLT-APGR方法对于现场实例1的计算结果(初值储量G a=70×108 m3)Table 16 Estimation of gas in place using VRRLT-APGR method with an initial G a=70×108 m3 for field case 1 |
| No. | G a /(108 m3) | m bdf /[10-4 MPa·(104 m3)-1] | G e /(108 m3) | E e /% |
|---|---|---|---|---|
| 1 | 70 | 1.244 823 953 | 43.790 658 518 | -37.442 |
| 2 | 43.790 658 518 | 1.246 540 738 | 43.730 348 299 | -0.138 |
| 3 | 43.730 348 299 | 1.246 547 072 | 43.730 126 095 | -0.001 |
| 4 | 43.730 126 095 | 1.246 547 098 | 43.730 125 182 | 0.000 |
| 5 | 43.730 125 182 | 1.246 547 098 | 43.730 125 182 | 0.000 |
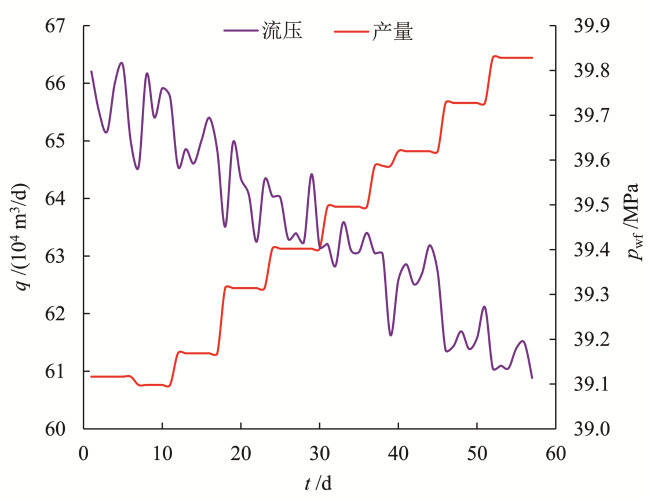
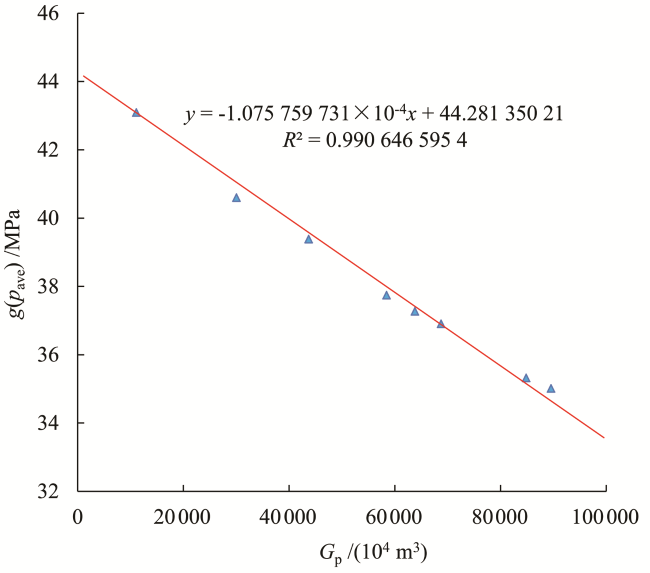
表17 B井的静压监测数据Table 17 Surveillance data of static pressure for Well B |
| p ave /MPa | G p /(104 m3) | Z(p ave) | p∙Z -1 /MPa | g(p ave) /MPa |
|---|---|---|---|---|
| 52.55 | 11 123.556 0 | 1.210 7 | 43.402 9 | 43.089 4 |
| 48.36 | 30 055.464 1 | 1.165 4 | 41.496 7 | 40.594 4 |
| 46.39 | 43 701.602 2 | 1.144 5 | 40.534 4 | 39.378 3 |
| 43.81 | 58 452.073 3 | 1.117 5 | 39.202 6 | 37.738 2 |
| 43.08 | 63 817.906 6 | 1.110 0 | 38.810 0 | 37.263 6 |
| 42.53 | 68 770.783 7 | 1.104 4 | 38.509 3 | 36.902 8 |
| 40.16 | 84 851.192 2 | 1.080 6 | 37.163 5 | 35.314 1 |
| 39.71 | 89 551.114 0 | 1.076 2 | 36.898 3 | 35.005 9 |
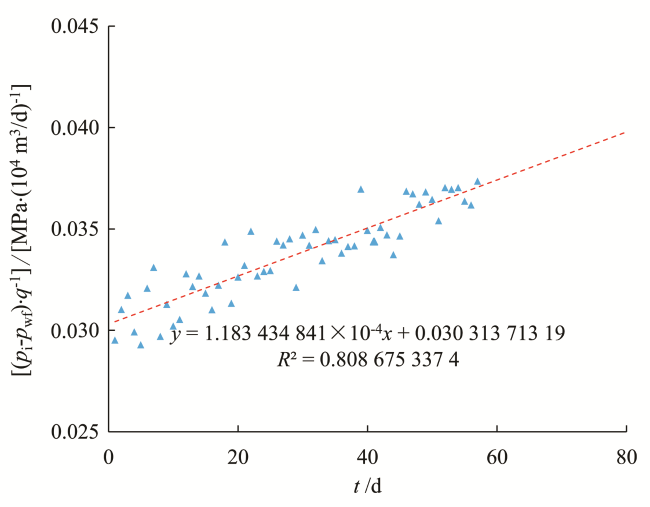
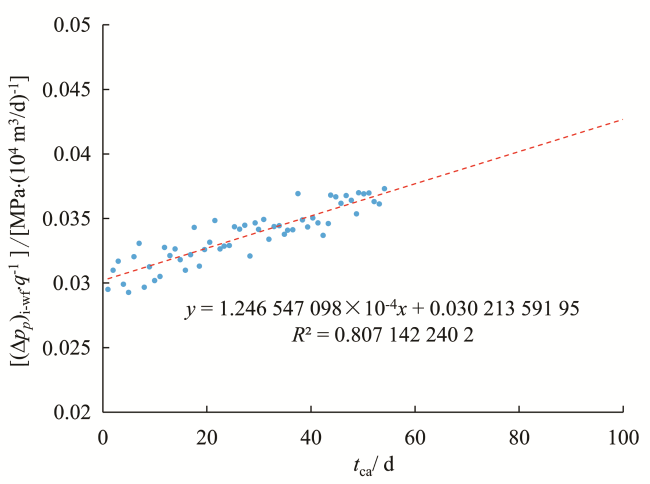
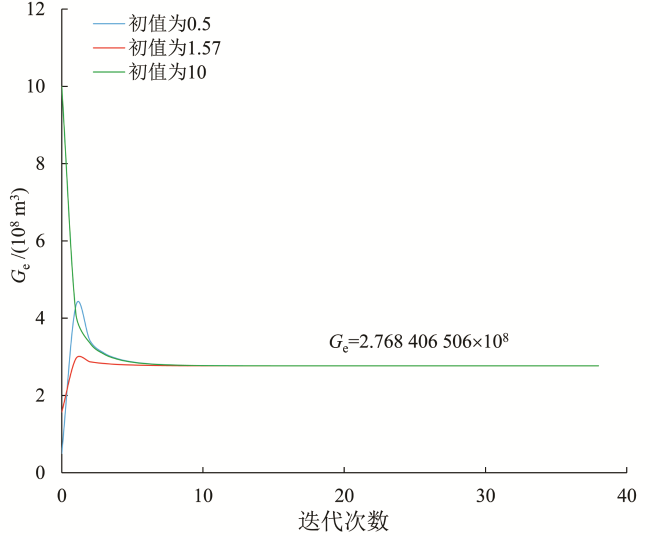
5.2 实例2
表18 VRRLT-APGR方法对于现场实例2的计算结果(初值储量G a=1.57×108 m3)Table 18 Estimation of gas in place using VRRLT-APGR method with an initial G a=1.57×108 m3 for field case 2 |
| No. | G a /(108 m3) | m bdf /[10-3 MPa·(104 m3)-1] | G e /(108 m3) | E e /% |
|---|---|---|---|---|
| 1 | 1.572 152 725 | 6.961 773 655 | 2.953 831 573 | 87.885 |
| 2 | 2.953 831 573 | 7.158 370 341 | 2.872 707 872 | -2.746 |
| 3 | 2.872 707 872 | 7.271 062 747 | 2.828 184 482 | -1.550 |
| 4 | 2.828 184 482 | 7.336 333 781 | 2.803 022 251 | -0.890 |
| 5 | 2.803 022 251 | 7.374 358 167 | 2.788 569 034 | -0.516 |
| 6 | 2.788 569 034 | 7.396 583 081 | 2.780 190 069 | -0.300 |
表19 VRRLT-APGR方法对于现场实例2的计算结果(初值储量G a=0.5×108 m3)Table 19 Estimation of gas in place using VRRLT-APGR method with an initial G a=0.5×108 m3 for field case 2 |
| No. | G a /(108 m3) | m bdf /[10-3 MPa·(104 m3)-1] | G e /(108 m3) | E e /% |
|---|---|---|---|---|
| 1 | 0.500 000 000 | 4.756 352 061 | 4.323 461 881 | 764.692 |
| 2 | 4.323 461 881 | 6.015 309 487 | 3.418 594 982 | -20.929 |
| 3 | 3.418 594 982 | 6.638 570 935 | 3.097 640 596 | -9.388 |
| 4 | 3.097 640 596 | 6.976 487 423 | 2.947 601 792 | -4.844 |
| 5 | 2.947 601 792 | 7.166 751 811 | 2.869 348 259 | -2.655 |
| 6 | 2.869 348 259 | 7.275 900 567 | 2.826 303 993 | -1.500 |
| 7 | 2.826 303 993 | 7.339 146 623 | 2.801 947 949 | -0.862 |
| 8 | 2.801 947 949 | 7.376 000 407 | 2.787 948 169 | -0.500 |
表20 VRRLT-APGR方法对于现场实例2的计算结果(初值储量G a=10×108 m3)Table 20 Estimation of gas in place using VRRLT-APGR method with an initial G a=10×108 m3 for field case 2 |
| No. | G a /(108 m3) | m bdf /[10-3 MPa·(104 m3)-1] | G e /(108 m3) | E e /% |
|---|---|---|---|---|
| 1 | 10.000 000 000 | 4.999 528 478 | 4.113 169 256 | -58.868 |
| 2 | 4.113 169 256 | 6.128 931 771 | 3.355 218 755 | -18.427 |
| 3 | 3.355 218 755 | 6.698 843 340 | 3.069 769 777 | -8.508 |
| 4 | 3.069 769 777 | 7.010 077 021 | 2.933 478 015 | -4.440 |
| 5 | 2.933 478 015 | 7.185 917 864 | 2.861 695 224 | -2.447 |
| 6 | 2.861 695 224 | 7.286 973 433 | 2.822 009 304 | -1.387 |
| 7 | 2.822 009 304 | 7.345 587 992 | 2.799 490 912 | -0.798 |
| 8 | 2.799 490 912 | 7.379 762 217 | 2.786 527 021 | -0.463 |



 甘公网安备 62010202000678号
甘公网安备 62010202000678号