天然气地球科学 >

2020 , Vol. 31 >Issue 6: 827 - 834

DOI: https://doi.org/10.11764/j.issn.1672-1926.2019.12.007

非常规天然气

适用于高温高压条件的等温吸附曲线方程

  • 彭泽阳 , 1, 2 ,
  • 龙胜祥 1, 2 ,
  • 张永贵 1, 2 ,
  • 卢婷 1, 2 ,
  • 王濡岳 1, 2
展开
  • 1. 中国石化石油勘探开发研究院非常规资源研究所，北京 100083
  • 2. 页岩油气富集机理与有效开发国家重点实验室，北京 100083

彭泽阳（1991-），男，新疆克拉玛依人，博士后，主要从事煤层气与页岩气开发研究.E-mail: .

收稿日期: 2019-11-04

  修回日期: 2019-12-16

  网络出版日期: 2020-06-17

收起

A new method of adsorption isotherm in high temperature and pressure

  • Ze-yang PENG , 1, 2 ,
  • Sheng-xiang LONG 1, 2 ,
  • Yong-gui ZHANG 1, 2 ,
  • Ting LU 1, 2 ,
  • Ru-yue WANG 1, 2
Expand
  • 1. Sinopec Petroleum Exploration and Production Research Institute, Beijing 100083, China
  • 2. State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development, Beijing 100083, China

Received date: 2019-11-04

  Revised date: 2019-12-16

  Online published: 2020-06-17

Supported by

The National Science and Technology Major Project(2016ZX05061-001)

The National Natural Science Foundation of China(41202103)

Fold

本文亮点

如何描述高温高压下页岩储层的吸附特征，以及如何利用实验室测定的一个温度下的等温吸附曲线，预测其他温度条件下的等温吸附曲线，对页岩气藏的开发评价具有重要意义。基于D-R吸附势模型，建立了适用于高温高压条件下的等温吸附曲线方程，同时该方程可以很好地预测不同温度条件下的等温吸附曲线。利用该方法，对鄂尔多斯盆地页岩120 ℃、30 MPa等温吸附实验数据取得了很好的拟合效果，同时预测出20~100 ℃吸附曲线。预测结果表明温度对绝对吸附量的最大吸附量没有影响，仅影响绝对吸附量随压力变化的增长速度，但温度会大幅影响过剩吸附量的最大值和高压时的下降趋势。

本文引用格式

彭泽阳 , 龙胜祥 , 张永贵 , 卢婷 , 王濡岳 . 适用于高温高压条件的等温吸附曲线方程[J]. 天然气地球科学, 2020 , 31(6) : 827 -834 . DOI: 10.11764/j.issn.1672-1926.2019.12.007

Highlights

It’s very important for the development of shale gas reservoir to describe the adsorption characteristics of shale gas reservoir, especially at high temperature and pressure and predict adsorption isotherms under different temperatures by one adsorption isotherms. Based on the D-R adsorption potential method, isothermal adsorption curve under high temperature and high pressure was established, which can predict the isothermal adsorption curve under different temperature. The method is fitting of the real data in Ordos Basin, with pressure from 0-30 MPa, and temperature at 120 ℃, and forecast their isotherms under 20-100 ℃. Results show that the temperature has no effect on the maximum adsorption capacity, only affect the change rate of absolute adsorption capacity with pressure, but the temperature will greatly affect the maximum amount of excess adsorption and the downward trend at high pressure.

0 引言

在页岩气藏的评价和开发过程中，储层条件下页岩的吸附能力是非常重要的关键参数之一[1]。目前针对页岩气吸附能力的评价主要采用室内岩样的等温吸附实验，但由于实验难度和设备精度问题，大部分等温吸附实验均在较低的温度和压力下进行[2,3,4,5,6,7,8]，而页岩气藏实际储层往往处在高温高压的条件下，低温低压的等温吸附实验与储层条件差异巨大，很难描述实际储层的吸附特征[9,10]，例如在高压条件下出现的随着压力的增加吸附量表现出先增大到最大值然后开始下降的现象[11,12]。
随着实验设备精度的提高，部分学者进行了高温（100~150 ℃）、高压（30 MPa）下的吸附实验，并对该条件下的吸附特征和影响因素进行研究，但这些研究一方面在研究过程中大量采用经验公式，使得最终的结果仅在研究区块具有较高的拟合效果，很难推广应用于其他页岩气储层；另一方面高温高压实验往往对实验花费和精力提出更高的要求，大多仅能获得1~3个不同温度下的高温高压实验结果，如果想要得到不同温度下页岩的等温吸附曲线，或研究厚层页岩气储层纵向不同温度分布对应的吸附能力分布，只能通过大量的重复实验获得[13,14,15]。因此，建立适用于高温高压条件、且方程中存在受储层温度影响关键参数的等温吸附曲线方程是十分必要的。
目前，国内外常用的等温吸附曲线解析模型可以分为以下4类：
第一类吸附模型是利用“气—固界面能”，建立固体表面的单位吸附量与平衡压力之间的关系，具有代表性的模型包括：Henry定律及Henry定律的修正模型等[16]。
第二类吸附模型是假设固相上存在一定数量的“吸附位”，利用气相分子进入吸附位和从吸附位离开的动态平衡，建立固体表面的单位吸附量与平衡压力之间的关系，具有代表性的模型包括：Langmuir单层分子吸附模型、BET多层分子吸附模型等[17,18]。
第三类吸附模型是假设固相表面存在吸附势能场，气体分子进入势场即发生吸附，建立固体表面的单位吸附量与平衡压力之间的关系，具有代表性的模型包括：Polanyi吸附势理论、D—A吸附模型和D—R吸附模型等 [9,19,20]；
第四类吸附模型是根据毛细凝聚的原理，利用“饱和蒸汽压”， 建立固体表面的单位吸附量与平衡压力之间的关系，具有代表性的模型包括：Laplace吸附模型与Kelvin吸附模型等 [16]。
考虑到第一类吸附模型虽然方程相对简便，但计算过程中所需参数难以获得，很难用于实际应用过程；第二类吸附模型尽管是目前页岩气、煤层气主要采用的吸附模型，但其本质为在“吸附位”和“单层吸附”的假设基础上由分子力学或热力学推导获得的半经验公式，很难从机理上对其参数进行修正使其满足高温高压和不同温度下的吸附特征，且很难拟合实际高温高压下的吸附实验数据；第三类吸附模型从分子势能出发，虽然仅限于物理吸附，但因为是热力学理论推导，不需要假设吸附层的实际物理模型，考虑到页岩气储层中甲烷的吸附也是物理吸附，因此更加适用；第四类吸附模型基于气液毛细凝聚理论与页岩气吸附机理不符，因此最终优选第三类吸附模型，建立适用于高温高压和不同温度下的页岩气等温吸附曲线模型。

1 模型推导

在页岩储层中，甲烷以超临界状态吸附于页岩储层的纳米孔隙中[10]，采用优选的第三类吸附模型中拟合精度更高，且相对更容易实际应用的D—A吸附模型，如式（1）所示[21]：
n a b s = n 0 e x p   [ - ( A E ) 2 ]
式中：n abs为绝对吸附量，mol/kg；n 0为最大吸附量，mol/kg；E为吸附系统的特征能量，J/mol；A为吸附势，J/mol，可由下式进行计算：
A = R ( T + 273.15 )   L n P 0 P
式中：R为理想气体常数，J/(mol·K)；T为温度，℃；P 0为饱和蒸汽压，MPa；P为压力，MPa。
从吸附势理论的公式中可以看出，吸附势理论主要以临界温度以下可以凝聚的气体为研究对象，此时气体物理吸附热与凝聚热相当，吸附相压力可以用饱和蒸汽压P 0表示 [16]。然而，实际页岩气储层温度远大于甲烷的临界温度-82.4 ℃，此时甲烷以超临界态存在 [22]，不能继续采用饱和蒸汽压P 0，因此需要采用虚拟饱和蒸汽压P *来替代饱和蒸汽压，本文采用AMANKWAH等 [23]提出的公式计算甲烷的虚拟饱和蒸汽压P *：
P * = P c ( T T c ) k
式中：P c为甲烷的临界压力，取4.59 MPa；T c为甲烷的临界温度，取-82.4 ℃；k为吸附特征值，该值主要受吸附剂和吸附质本身的性质影响，与温度压力无关，DUBININ [21]在描述超临界甲烷在活性炭上的吸附时将其简化为k=2的平方公式，也证明了该公式的可靠性。
联立式（1）—式（3），可以获得适用于页岩气超临界状态的D-R吸附模型：
n a b s = n 0 e x p   - R T E 2 L n 2 ( T T c ) k P c P
针对高压条件下等温吸附实验曲线随着压力的增加先增加后降低的现象，目前普遍认为实验室测量的是过剩吸附量而不是绝对吸附量。绝对吸附量是指被吸附的气体的含量，而过剩吸附量是指被吸附的气体含量减去如果未发生吸附、吸附气所占据区域原本应该充填的游离气量，因此，实验测得的过剩吸附量与绝对吸附量的关系可由下式给出 [9]：
n e x c = n a b s - v a d s ρ = n a b s ( 1 - ρ ρ a d s )
式中：n exc为过剩吸附量，mol/kg；V ads为吸附气所占体积，m3；ρ和ρ ads分别为该状态下的游离气密度和吸附气密度，kg/m3。
因此，适用于页岩气高温高压实验数据的D—R吸附模型为：
n e x c = ( 1 - ρ ρ a d s ) n 0 e x p   - R T E 2 L n 2 [ ( T T c ) k P c P ]
考虑到甲烷的分子量和页岩密度始终保持不变，因此可以将式（6）中单位质量的摩尔吸附量n直接转化为单位质量的体积吸附量V，如下所示：
V e x c = ( 1 - ρ ρ a d s ) V 0 e x p   - R T E 2 L n 2 [ ( T T c ) k P c P ]
式中：V exc为过剩吸附量，m3/t；V 0为最大吸附量，m3/t。
在该方程的实际应用过程中，通过一组高温高压等温吸附实验获得的不同压力下的过剩吸附量很难直接带入求解，因此需要将式（7）变形为如下形式：
L n V e x c ( 1 - ρ ρ a d s ) = a L n 2 P + b L n P + c
式中:a、b、c为拟合系数，可由下式决定：
a = - ( R T E ) 2
b = 2 ( R T E ) 2 L n   [ T T c k P c ]
c = L n V 0 - ( R T E ) 2 L n 2   [ T T c k P c ]
由此，可以将实验结果中的过剩吸附量与密度的比值 V e x c / ( 1 - ρ ρ a d s )和压力P在双对数坐标上绘图，则两者间存在二项式关系，且可由二项式各系数反推出公式参数。由此，可最终获得适用于高温高压，且与温度有关的等温吸附关系式。
与前人[9,20,24]的等温吸附曲线模型对比，尽管均与本文一样以D—A吸附模型为基础建立等温吸附曲线方程，最终建立的模型方程形式相似。但这些模型均未提及等温吸附实验数据的拟合过程，而是直接获得了拟合结果的图像，即直接将除了最大吸附量以外的参数人为输入再进行实验数据拟合，但实际生产过程中，吸附系统的特征能量E、吸附特征值k等参数均很难或无法获得，而通过本文提出的拟合方法，可以跳过关键参数的赋值过程，利用拟合二项式系数直接反推出最终公式，不仅具有更高的精度，也更具有实用性。

2 实例应用

取鄂尔多斯盆地页岩气样品，采用德国Rubotherm公司制造的ISOSORP-GAS SC磁悬浮天平重量法高压等温吸附仪器，利用重量法进行120 ℃条件下的高温高压等温吸附实验，其中，实验过程中吸附层密度获取方式为：假设实验数据满足高压下三元Langmuir方程，利用数据拟合得到测定吸附层密度为0.174 65，最终吸附结果如表1所示。
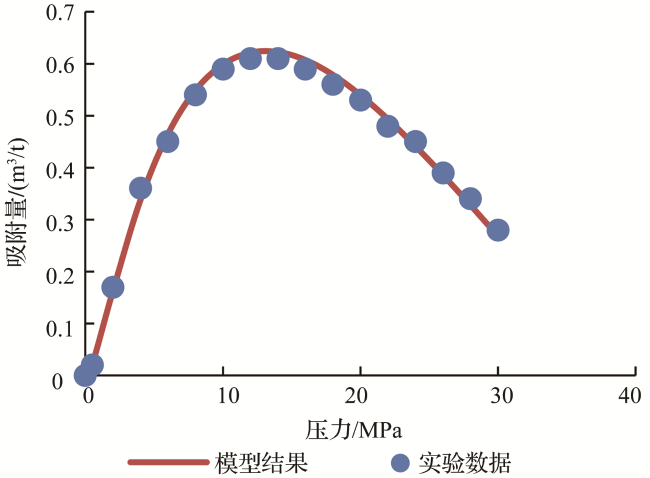
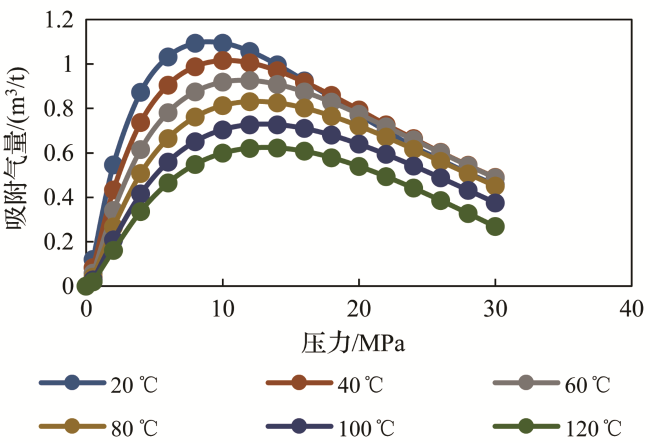
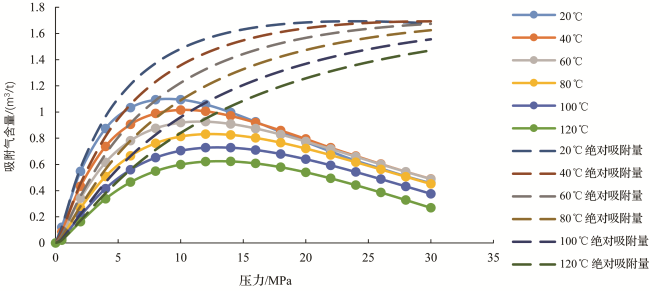
表1 120 ℃高温高压等温吸附实验结果

Table 1 Experiment result of adsorption in 120 ℃

记录编号

压力P

/MPa

气体密度

/(g/cm3）

吸附量V

/（m3/t）
0 0 0 0
1 0.5 0.002 39 0.020 571
2 2 0.009 75 0.161 564
3 4 0.019 8 0.464 039
4 6 0.029 88 0.548 433
5 8 0.040 04 0.598 39
6 10 0.050 23 0.621 236
7 12 0.060 37 0.622 567
8 14 0.070 44 0.607 22
9 16 0.080 35 0.578 551
10 18 0.090 11 0.539 605
11 20 0.099 67 0.493 167
12 22 0.108 95 0.441 138
13 24 0.117 94 0.385 727
14 26 0.126 55 0.327 71
15 28 0.134 84 0.268 18
16 30 0.142 8 0.464 039
对于吸附层密度ρ ads，根据POIRIER[25]在2014年针对不同条件下吸附层密度与压力之间的关系可以看出(图1)，尽管吸附层密度ρ ads在低压条件下随压力的变化存在显著变化，但在低压段吸附量较小，吸附相密度在宏观实验中可假定为固定值，而游离相密度在低压段较低且远低于吸附相密度，进而造成(1－ρ/ρ ads)值近似于1，即此时可采用绝对吸附量近似代替过剩吸附量。而当压力较高时，吸附层密度ρ ads几乎不再变化，因此在计算高压条件下过剩吸附量时，可以将吸附层密度ρ ads视为一个常数。
图1 吸附层密度与压力之间的关系[25]

Fig.1 Relationship between pressure and adsorbed phase density[25]

因此，忽略压力变化对吸附层密度的影响，采用实验获得的吸附层密度对实验结果进行拟合，得出的Ln[V/(1－ρ/ρ ads)]与LnP之间具有显著的二项式关系，如图2所示，证明模型推导及吸附层密度假设可靠。
图2 Ln[V/(1-ρ/ρ ads)]与LnP拟合曲线

Fig.2 Fitting curve of Ln[V/(1-ρ/ρ ads)] and LnP

根据拟合的二项式曲线可得：a=-0.176 8，b=1.518 2，c=-2.732 8，由式（9）—式（11）可反推出等温吸附曲线模型各参数的具体数值：
( R T E ) 2 = - a = 0.176   8
L n   T T c k P c = b 2 ( R T E ) 2 = b 2 a = 4.293    6
V 0 = e c + ( R T E ) 2 L n 2 T T c k P c = e c - a * ( b 2 a ) 2 = e c - b 2 4 a = 1.692   9
取甲烷的临界参数T c=-82.4 ℃，P c=4.59 MPa，代入式（13）可求出k=3.83，与文献[26]的计算结果(k值介于3.2~4.0之间，以3.6~3.9为主）吻合。
由此可获得适用于该页岩样品的高温高压等温吸附曲线模型，如下所示：
V e x c = 1 - ρ ρ a d s * 1.692   9 e x p   - 0.176   8 L n 2 [ ( T 190.7 ) 3.83 4.59 P ) ]
利用该公式反推120 ℃条件下等温吸附曲线，取得了很好的拟合效果，如图3所示。
图3 模型计算结果与实验数据对比

Fig.3 Curve of result of method and experiment data

当利用该公式预测其他温度的等温吸附曲线时，需要获得不同温度下甲烷游离气体密度ρ与吸附层密度ρ ads。其中，当前条件下甲烷游离气体密度ρ很容易获得，可在实验过程中通过实验一并获得，或查阅相关化学手册获得[27]。
而对于吸附层密度ρ ads，目前尚没有较好的获得方法，目前常用的吸附层密度计算经验公式局限性较大，仅对特定温度范围、特定固相具有较好的近似效果，对于研究区块的页岩存在较大的计算误差，常用计算方法的计算结果如表2所示。
表2 常用吸附层密度经验公式计算结果与实验测定结果对比

Table 2 Result of adsorbed phase density by experiment and empirical formula

数据来源 值
经验公式

Dubinin-Nikolaev方程[28]:

ρ a d s = ρ b - ρ b - ρ c T c - T b ( T - T b )

 0.237 7

Ozawa方程[29]:

ρ a d s = ρ b e x p   [ - 0.002   5 T - T b ]

 0.209 1

Dubinin方程[30] :

ρ a d s = ρ b e x p   [ - L n   ( b ρ b M ) T c - T b T - T b ]

 0.293 1
实验测定结果 0.174 65
本文通过对文献中不同条件下温度与吸附层密度关系进行统计[31]，发现吸附层密度与温度呈现显著的二项式关系，如图4所示。
图4 温度与吸附层密度关系统计

Fig.4 Relationship between temperature and adsorbed phase density

因此，假设温度与吸附层密度间满足二项式关系，根据实验实测吸附层密度与其余文献测定的吸附层密度，获得最终的温度与吸附层密度拟合关系 ρ a d s=-2.49×10-6 T 2+0.000 467+0.377，如表3所示。
表3 温度与吸附层密度拟合数据来源及结果

Table 3 Data in fitting equation of temperature and adsorbed phase density

拟合参数 拟合方程计算结果
T/℃ ρ ads/(g/cm3） 数据来源
-82.5 0.375 LI[31] 0.375
120 0.174 65 实验测定 0.175
-40.15 0.35 ZHOU[32] 0.35

3 影响因素分析

将不同温度、压力条件下的甲烷游离气密度和吸附层密度带入式（15），即可获得不同温度、压力条件下的等温吸附曲线方程，如图5所示，同时计算不考虑密度的绝对吸附量的等温吸附曲线方程，如图6所示。
图5 不同温度吸附曲线预测

Fig.5 Prediction curve of excess adsorption under different temperature

图6 不同温度绝对吸附曲线预测

Fig.6 Prediction curve of absolute adsorption different temperature

由此，可获得温度对高压等温吸附曲线的影响：
（1）随着温度的升高，绝对吸附量的最大吸附量几乎不变，仅增长趋势发生变化，即温度越高，达到最大吸附量所需的压力越大。这与目前国内外学者的研究结果相同，LI等[33]、ZHANG等[34]通过分子模拟均得到了随着温度的提升，最大吸附量保持不变的结果，而GASPARIK等[35]总结认为，在38~150 ℃范围内可以认为最大吸附量不随温度的变化而变化。从理论出发，对于物理吸附，最大吸附量仅取决于物质本身的性质和固体的比表面积，而温度对物质本身的性质和固体的比表面积均无法影响，因此随着温度的变化绝对吸附量的最大吸附量保持不变[36]。
也有部分学者认为温度对最大吸附量有一定的影响关系，主要有2种不同的认识：第一类认为温度虽然对最大吸附量影响较小，但仍有一定的影响 [2,3,4,5,17]；第二类则认为温度会造成固相比表面积破坏，导致最大吸附量随温度急剧下降[37,38,39]。
综合该类文献，发现第一类主要出现在利用Langmuir理论对不同温度条件下煤页岩的吸附实验数据进行拟合获得的结论，由于Langmuir理论拟合过程中包含2个参数，即兰氏体积V L和兰氏压力P L，因此从数学上看，在兰氏体积V L变化幅度较低时，可以保持兰氏体积V L不变，通过拟合兰氏压力P L获得相似或者更高的精度，即温度造成最大吸附量的微小变化可视作数学拟合过程中的误差。而第二类主要研究对象为含水页岩，并不是干燥页岩。综上所述，温度的变化不影响绝对吸附量的最大吸附量。
（2）随着温度的升高，过剩吸附量的峰值和下降速度均发生变化，这是由于随着温度的增加，气体密度与吸附相密度均发生变化，且温度较低时，吸附相密度随温度升高变化更为敏感，由此导致气体密度与吸附相密度随温度的升高下降速率不同，(1－ρ/ρ ads)始终保持变化；而当温度较高时，吸附相密度随温度升高变化与气相密度随温度升高变化趋势几乎相同，由此导致(1－ρ/ρ ads)几乎保持不变。体现在曲线上即为：温度低于60 ℃时，随着温度的增加，过剩吸附量降低速率逐渐减缓，而当温度大于60 ℃时，随着温度的增加过剩吸附量降低速率基本不变，体现在曲线上为各温度尾部下降曲线几乎平行。

4 结论

（1） 建立了适用于鄂尔多斯盆地页岩的高温高压等温吸附曲线，且能够用该曲线预测其他温度吸附曲线。以D—R吸附理论为基础，建立考虑温度影响的高温高压等温吸附曲线，并通过建立的鄂尔多斯盆地页岩的吸附层经验公式和实验数据拟合，建立了适用于该页岩样品的高温高压等温吸附曲线模型，利用该公式反推120 ℃条件下等温吸附曲线，取得了很好的拟合效果。
（2） 分析了储层温度对页岩吸附能力的影响。随着温度的升高，绝对吸附量的最大吸附量几乎不变，仅增长趋势发生变化，即温度越高，达到最大吸附量所需的压力越大。同时，随着温度的升高，过剩吸附量的峰值和下降速度均发生变化：当温度低于60 ℃时，随着温度的增加，过剩吸附量降低速率逐渐减缓，而当温度大于60 ℃时，随着温度的增加过剩吸附量降低速率基本不变，体现在曲线上为各温度尾部下降曲线几乎平行。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
1
李相方,蒲云超,孙长宇,等.煤层气与页岩气吸附/解吸的理论再认识[J].石油学报,2014,35(6):1113-1129.

LI X F, PU Y C, SUN C Y, et al. Recognition of absorption/desorption theory in coalbed methane reservoir and shale gas reservoir[J]. Acta Petrolei Sinica, 2014, 35(6): 1113-1129.

2
李武广,杨胜来,陈峰,等.考虑地层温度和压力的页岩吸附气含量计算新模型[J].天然气地球科学,2012,23(4):791-796.

LI W G, YANG S L, CHEN F, et al. A new model for shale adsorptive gas amount under a certain geological conditions of temperature and pressure[J]. Natural Gas Geoscience,2012,23(4):791-796.

3
郭为,熊伟,高树生,等.温度对页岩等温吸附/解吸特征影响[J].石油勘探与开发,2013,40(4):481-485.

GUO W, XIONG W, GAO S S, et al. Impact of temperature on the isothermal adsorption/desorption characteristics of shale gas[J]. Petroleum Exploration and Development, 2013,40(4):481-485.

4
杨峰,宁正福,张睿,等.甲烷在页岩上的吸附等温过程[J].煤炭学报,2014,39(7):1327-1332.

YANG F, NING Z F, ZHANG R, et al. Adsorption isotherms process of methane on gas shales[J]. Journal of China Coal Society, 2014,39(7):1327-1332.

5
杨峰,宁正福,王庆,等.甲烷在页岩上吸附的热力学[J].中南大学学报:自然科学版,2014,45(8):2871-2877.

YANG F, NING Z F, WANG Q, et al. Thermodynamic analysis of methane adsorption on gas shale[J]. Journal of Central South University:Science and Technology, 2014,45(8):2871-2877.

6
闫建萍,张同伟,李艳芳,等.页岩有机质特征对甲烷吸附的影响[J].煤炭学报,2013,38(5):805-811.

YAN J P, ZHANG T W, LI Y F, et al. Effect of the organic matter characteristics on methane adsorption in shale[J]. Journal of China Coal Society, 2013,38(5):805-811.

7
赵玉集,郭为,熊伟,等.页岩等温吸附/解吸影响因素研究[J].天然气地球科学,2014,25(6):940-946.

ZHAO Y J, GUO W, XIONG W, et al. Study of impact factors on shale gas adsorption and desorption[J]. Natural Gas Geoscience, 2014,25(6):940-946.

8
赵金,张遂安,曹立虎.页岩气与煤层气吸附特征对比实验研究[J].天然气地球科学,2013,24(1):176-181.

ZHAO J, ZHANG S A, CAO L H. Comparison of experimental adsorption between shale gas and coalbed gas[J]. Natural Gas Geoscience, 2013,24(1):176-181.

9
REXER T F T, BENHAM M J, APLIN A C, et al. Methane adsorption on shale under simulated geological temperature and pressure conditions[J]. Energy Fuels, 2013, 27(6): 3099-3109.

10
ROSS D J K, BUSTIN R M. Characterizing the shale gas resource potential of Devonian-Mississippian strata in the Western Canada sedimentary basin: Application of an integrated formation evaluation[J]. AAPG Bulletin, 2008, 92(1): 87-125.

11
杨峰,宁正福,孔德涛,等. 页岩甲烷吸附等温线拟合模型对比分析[J]. 煤炭科学技术, 2013,41(11):86-89.

YANG F, NING Z F, KONG D T, et al. Comparison analysis on model of methane adsorption isotherms in shales[J]. Coal Science and Technology, 2013, 41(11): 86-89.

12
林腊梅,张金川,韩双彪,等. 泥页岩储层等温吸附测试异常探讨[J]. 油气地质与采收率, 2012, 19(6): 30-33.

LIN L M, ZHANG J C, HAN S B, et al. Study on abnormal curves of isothermal adsorption of shale[J]. Petroleum Geology and Recovery Efficiency, 2012, 19(6): 30-33.

13
刘尚平,李希建,尹鑫,等.高温高压下页岩气等温吸附线拟合模型优选[J].中国矿业,2018,27(6):160-166.

LIU S P, LI X J, YIN X, et al. Optimal model of isothermal adsorption for shale gas under high temperature and high pressure[J]. China Mining Magazine, 2018, 27(6): 160-166.

14
GASPARIK M, BERTIER P, GENSTERBLUM Y, et al. Geological controls on the methane storage capacity in organic-rich shales[J]. International Journal of Coal Geology, 2013,123(2):34-51.

15
李希建, 李维维, 黄海帆, 等. 深部页岩高温高压吸附特性分析[J]. 特种油气藏, 2017,24(3):129-134.

LI X J, LI W W, HUANG H F, et al. Analysis on adsorption characteristics of deep shale under high temperature and high pressure[J]. Special Oil & Gas Reservoirs, 2017,24(3):129-134

16
近藤精一(日,石川达雄(日,安部郁夫(日.吸附科学[M].北京:化学工业出版社,2006.

SEIICHI K, TATSUO I, IKUO A. The Adsorption Science[M]. Beijing:Chemical Industry Press,2006.

17
LANGMUIR I. The evaporation, condensation and reflection of molecules and the mechanism of adsorption[J].Journal of the Franklin Institute,1916,8(2):149-176.

18
BRUNAUER S, EMMETT P, TELLER E. Adsorption of gases in multimolecular layers[J]. Journal of the American Chemical Society, 1938, 60(2): 309-319.

19
POLANYI M. The potential theory of adsorption[J].Science,1963,141(3585):1010-1013.

20
HIMENO S, KOMATSU T, FUJITA S. High-pressure adsorption equilibria of methane and carbon dioxide on several activated carbons[J]. Journal of Chemical & Engineering Data,2005,50(2):369-376.

21
DUBININ M M. The potential theory of adsorption of gases and vapors for adsorbents with energetically nonuniform surfaces[J]. Chemical Reviews,1960,60(2):235-241.

22
张受谦. 化工手册[M].济南:山东科学技术出版社,1986.

ZHANG S Q. Handbook of Chemical[M]. Jinan:Shandong Technology Press,1986.

23
AMANKWAH K A G, SCHWARZ J A. A modified approach for estimating pseudo-vapor pressures in the application of the Dubinin-Astakhov equation[J].Carbon,1995,33(9):1313-1319.

24
REN W X, LI G S, TIAN S C, et al. Adsorption and surface diffusion of supercritical methane in shale[J]. Industrial & Engineering Chemistry Research, 2017, 56(12): 3446-3455.

25
POIRIER E. Ultimate H2 and CH4 Adsorption in slit-like carbon nanopores at 298 K: A molecular dynamics study[J]. RSC Advances, 2014,4(44):22848-22855.

26
李靖,李相方,王香增,等.“一点法”不同温度吸附曲线预测模型[J].天然气地球科学,2016,27(6):1116-1127.

LI J, LI X F, WANG X Z, et al. A new method to predict adsorption isotherms under different temperatures[J]. Natural Gas Geoscience, 2016,27(6):1116-1127.

27
SETZMANN U, WAGNER W. A new equation of state and tables of thermodynamic properties for methane covering the range from the melting line to 625 K at pressures up to 1 000 MPa[J]. Journal of Physical and Chemical Reference Data, 1991, 20(6):1061-1151.

28
NAKAHARA T, HIRATA M, OHMORI T, et al. Adsorption of hydrocarbons on carbon molecular sieve[J]. Journal of Chemical & Engineering Data, 1974, 19(4): 310-313.

29
OZAWA S, KUSUMI S, OGINO Y. Physical adsorption of gases at high pressure, IV: An improvement of the Dubinin-Astakhov adsorption equation[J]. Journal of Colloid and Interface Science, 1976, 56(1): 83-91.

30
DUBININ M M. Generalization of the theory of volume filling of micropores to nonhomgeneous microporous structures[J]. Carbon, 1985, 23(4):373-380.

31
LI J, WU K, CHEN Z, et al. On the negative excess isotherms for methane adsorption at high pressure: Modeling and experiment[J]. SPE Journal, 2019, 24(6): 2504-2525.

32
周理,李明,周亚平. 超临界甲烷在高表面活性炭上的吸附测量及其理论分析[J] .中国科学:B辑,2000, 30(1):49-56.

ZHOU L, LI M, ZHOU Y P. The adsorption measurement and theoretical analysis of supercritical methane in high on the surface of activated carbon[J]. Science in China:Series B,2000,30(1):49-56.

33
LI X J, LIN B Q, XU H. Monte carlo simulation of methane molecule adsorption on coal with adsorption potential[J].International Journal of Mining Science and Technology,2014,24(1):17-22.

34
ZHANG J F, CLENNELL M B, DEWHURST D N,et al.Combined Monte Carlo and molecular dynamics simulation of methane adsorption on dry and moist coal[J].Fuel,2014,122(15):186-197.

35
GASPARIK M, BERTIER P, GENSTERBLUM Y, et al. Geological controls on the methane storage capacity in organic-rich shales[J].International Journal of Coal Geology,2013,123(2):34-51.

36
JIN Z, FIROOZABADI A. Methane and carbon dioxide adsorption in clay-like slit pores by Monte Carlo simulations[J].Fluid Phase Equilibria,2013,360(25):456-465.

37
唐书恒,范二平.富有机质页岩中主要黏土矿物吸附甲烷特性[J].煤炭学报,2014,39(8):1700-1706.

TANG S H, FAN E P. Methane adsorption characteristics of clay minerals in organic-rich shales[J]. Journal of China Coal Society,2014,39(8):1700-1706.

38
KAUFHOLD S, DOHRMANN R, KLINKENBERG M, et al. N2-BET specific surface area of bentonites[J].Journal of Colloid and Interface Science,2010,349(1):275-282.

39
LIU D, YUAN P, LIU H,et al.High-pressure adsorption of methane on montmorillonite,kaolinite and illite[J].Applied Clay Science,2013,85(11):25-30.

Options
文章导航

/

〈 〉

陇ICP备2021001824号-7　 甘公网安备 62010202000678号
版权所有 © 《天然气地球科学》编辑部
地址：甘肃省兰州市天水中路8号　
邮编：730000　
电话：(0931)8277790　
E-mail：geogas@lzb.ac.cn
总访问量 　 今日访问 　 在线人数
技术支持：北京玛格泰克科技发展有限公司