0 引言
1 可变临界孔隙度Nur模型与方法
1.1 方法构想与改进
1.2 横波速度估算基本方法
1.3 Nur模型
1.4 可变临界孔隙度Nur模型
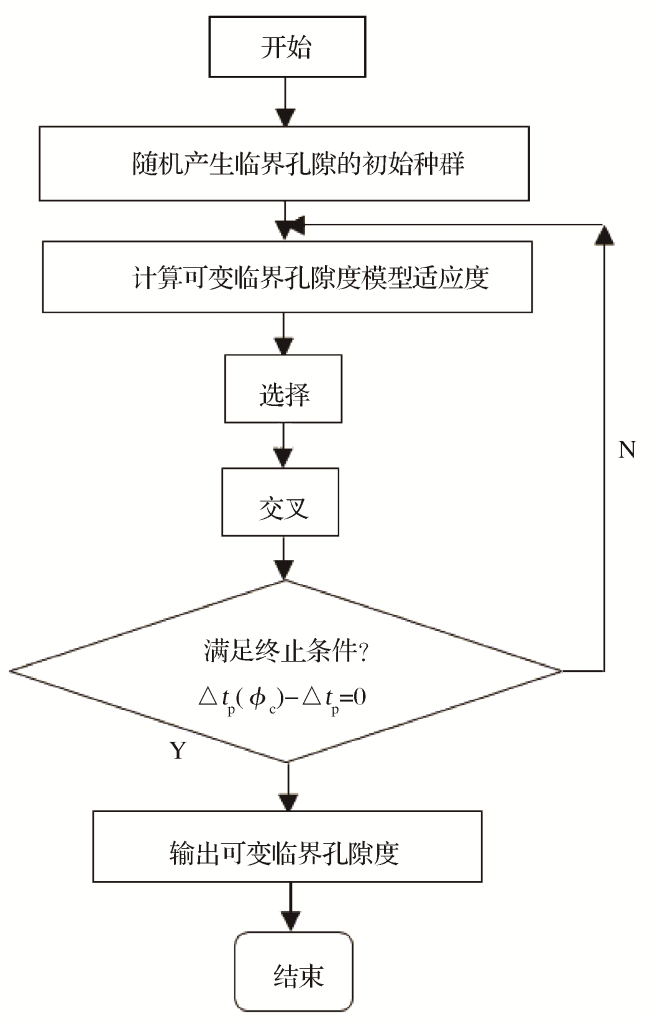
2 基于遗传方法的临界孔隙度计算
2.1 编码
2.2 初始群体的产生
2.3 杂交
2.4 适应度值评估检测
2.5 选择
2.6 变异
2.7 中止(误差控制)
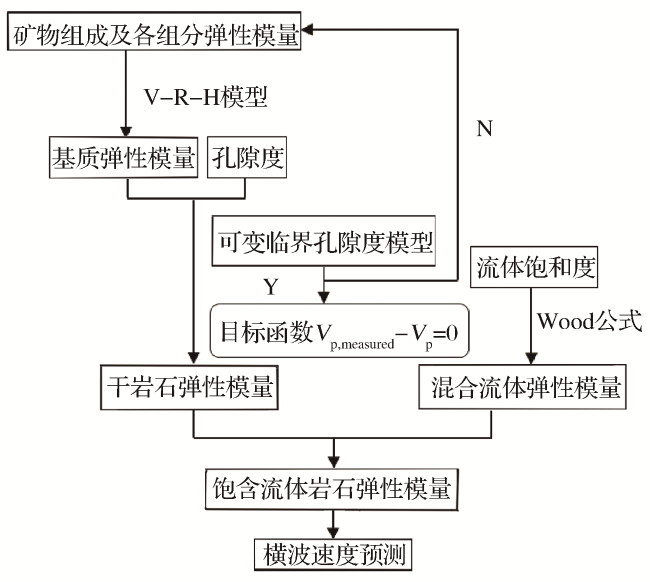
3 横波速度预测过程
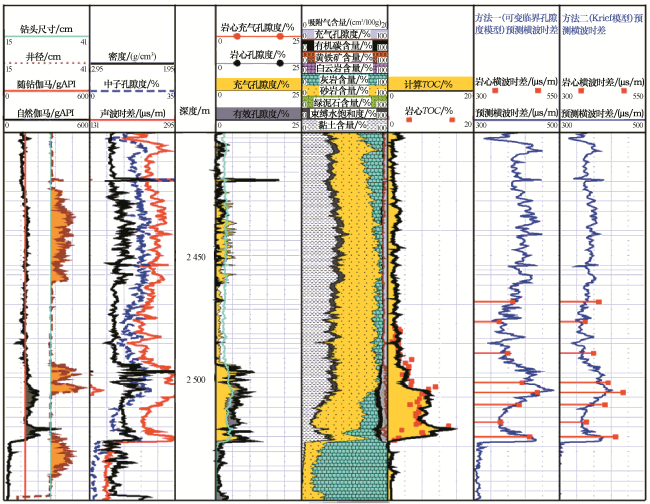
4 方法验证
表1 两种方法预测横波时差与DSI实测值对比Table 1 Prediction of shear wave time difference and DSI measured values by two methods |
| 深度/m | DSI实测横波时差/(μs/m) | 可变临界孔隙度预测横波时差/(μs/m) | Krief模型预测横波时差/(μs/m) |
|---|---|---|---|
| 2 469 | 411 | 412 | 375 |
| 2 477 | 383 | 378 | 354 |
| 2 490 | 397 | 401 | 368 |
| 2 502 | 479 | 456 | 408 |
| 2 506 | 485 | 485 | 440 |
| 2 511 | 408 | 410 | 434 |
| 2 518 | 375 | 376 | 367 |
| 2 524 | 470 | 468 | 413 |




 甘公网安备 62010202000678号
甘公网安备 62010202000678号