0 引言
近年来，随着深层气藏的开发，由于其储层埋藏较深，压力较大，压力对扩散的影响引起了人们的关注。林晨等［1］通过对气煤煤粒进行等温吸附扩散实验，发现气体的压力对于气体的扩散系数影响显著，扩散系数随着气体压力的增大而增大；NANDI等［2］、BIELICKI 等［3］、CUI 等［4］、袁军伟［5］认为甲烷的扩散速率随着压力的增大而增大，主要原因是多孔介质对甲烷吸附非线性造成的；刘彦伟［6］、李志强等［7］认为甲烷在注入多孔介质之后，迅速扩散，初期扩散速度极快而后随着时间增大扩散速度逐渐减慢，并且压力越高，甲烷扩散系数越大；KIM等［8］、MENG 等［9］通过实验得出气体的扩散系数随着压力的增大而减少。
虽然人们对于压力是否有利于气体扩散的看法并不统一，但大多数的研究均认为压力的增大有利于气体扩散。这些研究都把气体扩散量的增加归结于传统意义上的扩散系数的增大，并没有人从理论上来研究压力对于气体扩散的影响。
朱维耀［10］认为天然气扩散过程中，其扩散的原动力为化学势梯度扩散，而压力和浓度都是引发化学势变化的原因，据此提出了膨胀扩散系数的概念并推导出了压力作用下的气体的对流扩散模型。本文对原有模型进行改进，增加了解吸项，并在运动方程中考虑了气体在致密砂岩气藏流动过程中碰撞、滑移现象，使模型可以描述气体在致密砂岩储层中的流动规律，并采用有限差分法进行了数值模拟研究。从而在理论上搞清压力引起的膨胀扩散的作用条件和范围，明确压力对气体扩散速度影响的本质原因，理清压力引起的膨胀扩散的影响因素，揭示高压气体扩散渗流规律，准确掌握天然气开采过程压力、浓度的变化规律，为天然气气藏特别是高压致密砂岩气的开采提供理论指导。
1 模型建立
本模型及之后的模拟均基于以下假设：气体为理想气体，符合理想气体状态方程；不考虑温度、湿度对气体对流、扩散行为的影响；气体的扩散其本质上是由于气体的化学势梯度所引起。朱维耀［10］从化学势梯度推导出了考虑压力作用下的气体扩散对流方程：
式中：c为物质的体积浓度或质量浓度，单位为%或g/m3；t为时间，s；D为流体的扩散系数，m2/s；G为膨胀扩散系数，m2/（Pa·s）；p为压力，Pa；Q为源（汇）项强度，s-1。
相比于传统的扩散渗流方程考虑压力作用下的气体扩散对流方程增加由压力梯度所引起的扩散项，这对于高压条件下的气体扩散行为描述更为准确，对于高压气藏的开采也更具指导性的意义。为了求解此方程，还需补充如下辅助方程。
式中：kn为努森数，无量纲；λ为分子平均自由程，nm；r为孔喉直径，nm。v为流体的速度，m/s；k为渗透率，10-3 μm2；μ为流体黏度，Pa·s；a为与努森数kn有关的修正系数，无量纲，当0<kn<0.001时，a=0，当0.001<kn<0.01时，a=1.2，当0.01<kn<10时，a=1.34。本文所研究的致密砂岩气储层的孔隙半径小于50 μm，压力在0.1~100 MPa之间，此时气体的流动状态属于滑移流动，即0.001<kn<0.01，修正系数a取1.2［12］。
式中：η为导压系数，m2/s；ϕ为孔隙度，%；Ct为岩石压缩系数，Pa-1；P为压力的平方，Pa2。
气体在地层内部解吸附方程式［13］：
式中：V a为气体的解吸量，m3/kg；V L为Langmuir体积常数，m3/kg；p L为Langmuir压力常数，Pa。
源汇项计算公式：
式中：ρ s为岩石的密度，kg/m3。
将方程式（4） 、式（5） 代入方程式（1） ，同时令：
联合方程式（3） 可得考虑解吸和压力作用的气体扩散渗流模型为：
2 模型求解方法与模型验证
2.1 模型求解方法
采用有限差分法进行模型求解，方程式（3） 中的第一个方程中P的隐式差分格式［14］：
式中：Δt为时间间隔，s；Δx为空间间隔，m。
由差分方程式（8） 可得，在已知t时刻压力分布的情况下，通过求解方程组的方法求出t+1时刻的P的分布，结合方程式（3） 和初始条件即可求得不同时间下模型的压力分布。在求得压力分布后，将所求c代入方程式（7） 中的第一个方程后对浓度c进行显示差分［14］，则方程式（7） 的离散方程式可表示为：
同理可以通过求解方程组的方法来求得不同时刻下浓度c的分布。
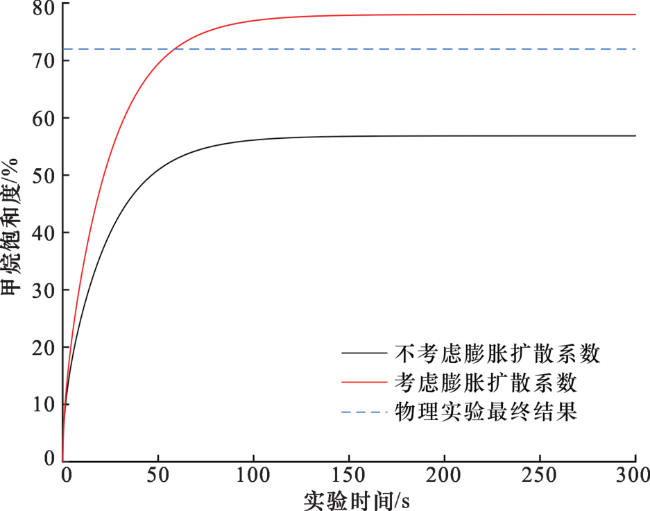
2.2 模型验证
表1 鄂尔多斯盆地苏里格气田致密砂岩气物理实验基本参数[15-17]Table 1 Basic parameters of tight sandstone gas physical experiment in Sulige Gas Field, Ordos Basin[15-17] |
| 参数 | 取值 |
|---|---|
| 岩心密度/（kg/m3） | 2 500 |
| 岩心渗透率/（10-3 μm2） | 0.1 |
| 岩心孔隙度/% | 3 |
| 岩心压缩系数/Pa-1 | 1.45×10-10 |
| 岩心长度/m | 0.05 |
| 岩心直径/m | 0.025 |
| 模拟流体 | 甲烷 |
| 气体密度/（g/m3） | 716 |
| Langmuir体积常数/(m3/kg) | 4.199×103 |
| Langmuir压力常数/Pa | 4.55×106 |
| 气体扩散系数/（m2/s） | 12×10-7 |
| 气体膨胀扩散系数/[m2/(Pa·s)] | 5×10-5 |
| 气体黏度/（mPa·s） | 0.011 |
表2 鄂尔多斯苏里格气田致密砂岩气岩心模拟参数Table 2 Core simulation parameters of tight sandstone gas in Sulige Gas Field, Ordos Basin |
| 物理量 | 取值 | |
|---|---|---|
| 网格参数 | 网格大小/m | 0.001 |
| 网格数量 | 50 | |
| 初始条件 | c(x,0)/% | 0 |
| p(x,0)/Pa | 0 | |
| 边界条件 | c(0,t)/% | 1 |
| c(L,t)/% | 0 | |
| p(0,t)/Pa | 100 000 | |
| p(L,t)/Pa | 0 |
由图1可知，随着甲烷气体充注的进行，岩心内部的甲烷的饱和度逐渐趋于一个定值，此即为岩心内部最终的甲烷饱和度。考虑压力扩散项时甲烷最终饱和度为76%左右，不考虑压力扩散项时甲烷最终饱和度为56%左右，物理实验甲烷最终饱和度为72%。所以本文模型与实际物理实验吻合度良好，验证了本文所用数学模型的准确性，通过对比可知考虑压力扩散时模型更为准确。
3 影响因素分析
3.1 模拟参数
通过有限差分法进行模型求解，模拟一维的天然气开发过程中地层内天然气浓度场的变化，以探究模型的适用性和影响因素。此节主要求解天然气的质量浓度，g/m3。简化后的一维物理模型如图2所示。
理想气体状态方程［13］：
式中：p为压力，Pa；M为质量，g；ρ为密度，g/m3；R为气体状态常数；T为温度，K。
根据理想气体状态方程［13］，如果假设地层压力为p w，求得此压力下地层内甲烷的质量浓度为：
式中： 为压力 下甲烷的质量浓度，g/m3；ρ为一个大气压下甲烷的密度，g/m3；
表3 鄂尔多斯盆地苏里格气田致密砂岩气一维模拟参数Table 3 One dimensional simulation parameters of tight sandstone gas in Sulige Gas Field, Ordos Basin |
| 参数 | 取值 | |
|---|---|---|
| 网格参数 | 网格大小/m | 25 |
| 网格数量 | 120 | |
| 初始条件 | C(x,0)/（g/m3） | 200 480 |
| p(x,0)/MPa | 28 | |
| 边界条件 | c（0，t） | 0 |
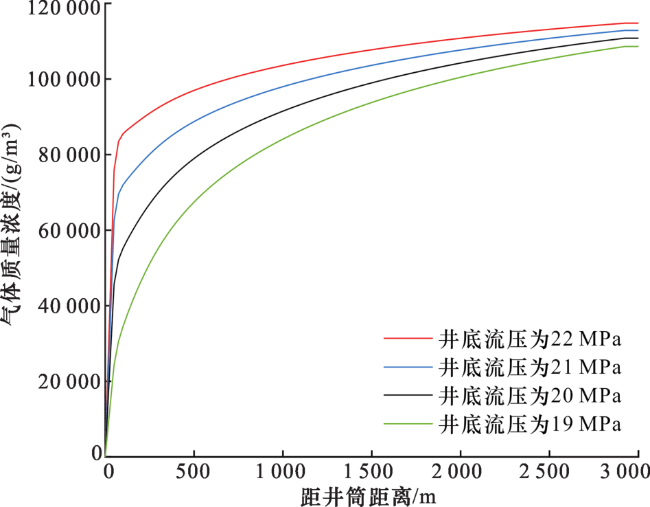
| p(0,t)/MPa | 22 |
3.2 影响因素分析
3.2.1 膨胀扩散系数
经过计算不同开采时间地层甲烷浓度的变化，如图3所示。随着开采时间的增加，地层内部浓度逐渐降低，由井筒向外地层甲烷浓度逐渐增高。在相同时间下考虑膨胀扩散系数比不考虑膨胀扩散系数地层甲烷浓度低。开采5年、10年、15年地层甲烷浓度依次降低12.3%、10.4%、8.8%，所以开采初期需要考虑膨胀扩散系数对于浓度的影响。以10年为例，考虑膨胀扩散系数比不考虑膨胀扩散系数地层整体浓度下降10.4%，其中距离井筒0~1 000 m、1 000~2 000 m、2 000~3 000 m平均浓度分别下降15%、8%、5%，在1 000 m以内浓度差别已经超过10%，所以对于井筒1 000 m以内地层甲烷浓度预测时要考虑压力引起的扩散项。造成上述现象的主要原因有2点：一是开采初期，地层内部压力梯度大，天然气流速较快，此时天然气的运移以对流方式为主，开采后期，地层压力梯度降低，天然气的主要运移方式逐渐由对流转为扩散；二是由于开采初期和近井地带压力梯度在空间上的变化率越大，导致压力引起的扩散项越大，进而压力引起的扩散量越大。
3.2.2 原始地层压力
通常把2 000 m到3 500 m深度的储层定义为中深层储层，把3 500 m到4 500 m深度的储层定义为深层，把4 500 m以浅深度的储层定义为超深层。对于正常压力的储层，其原始地层压力随深度变化可由同深度静水压力计算得出［18］：
式中：ρ L为水的密度，kg/m3；g为重力加速度，m/s2，h为储层深度，m。
分别对中深层（30 MPa）、深层（40 MPa）及超深层（50 MPa）储层浓度进行模拟。以开发10年为例，如图4所示，在相同开采时间下，随着原始地层压力的增加，地层甲烷浓度越来越高，这主要是由于其初始地层甲烷浓度高所导致的。并且随着初始地层压力的增加，考虑膨胀扩散系数比不考虑膨胀扩散系数下降程度越来越大，其中地层原始压力为30 MPa、40 MPa、50 MPa时浓度分别下降10.8%、12.5%、15.4%，所以中深层以上气藏的浓度场模拟时需考虑膨胀扩散系数的影响。
3.2.3 渗透率
随着低渗气藏的开采，常常出现气藏地层甲烷浓度预测与实际不符的情况，进而导致产能预测出现偏差。经过对不同渗透率地层甲烷浓度的模拟，发现这与本文所讨论的膨胀扩散系数有关（图5）。研究结果表明：以开采10年为例，随着地层渗透率的增加，考虑膨胀扩散系数比不考虑膨胀扩散系数地层甲烷浓度下降程度越来越小。其中地层渗透率为0.1×10-3 μm2、0.3×10-3 μm2、0.6×10-3 μm2、1×10-3 μm2分别下降10.4%、6.7%、4.8%、2.5%，所以，对于1×10-3 μm2以下的低渗气藏须考虑压力引起的扩散项（当渗透率大于2×10-3 μm2时，差别小于1%，可不考虑膨胀扩散系数）。
根据模型分析，造成这种现象的主要原因是渗透率越小，压力变化越剧烈，导致压力所引起的扩散越明显。
地层渗透率是影响天然气产量的重要因素，通常来讲，随着地层渗透率的增加，在相同开采时间下地层甲烷浓度越低。但是在考虑膨胀扩散系数的情况下，0.1×10-3 μm2相对于其他高渗透率地层来说其在近井地带其地层甲烷浓度反而略微增长。这是因为在地层内部物质的运移方式主要是对流和扩散，随着渗透率的增加，天然气流速越快，对流量越大，但压力引起的扩散项是随着渗透率的增加而降低的且其影响范围主要为近井地带。所以在近井地带，当压力作用下的扩散项的贡献程度大于对流项的贡献程度时，就会导致其浓度随着渗透率的增加而略微增加。
3.2.4 井底流压
降低井底流压，是油田常用的增产方法之一。从图6可以看出，在原始地层压力和开采时间一定时，随着井底流压降低，地层内部浓度逐渐降低。其中，19 MPa比22 MPa在距离井筒0~1 000 m、1 000~2 000 m、2 000~3 000 m时平均浓度分别下降31%、15%、8.3%，距离井筒越远差别越小，这主要因为距离井筒越近，压力梯度越大且压力梯度变化越剧烈，天然气对流量与压力所引起的扩散量越大。由于远井地带浓度几乎没有变化，所以降低井底流压并不能把距离井筒较远的天然气开采出来。
3.2.5 分子扩散系数
分子扩散系数是传统模型中唯一的扩散系数，对扩散现象有重要的影响且通过不同的测量手段所测得的值差别很大，基本位于10-7~10-6 m2/s之间［19-21］。从图7可以看出，随着分子扩散系数的减小，地层内部扩散现象变弱，地层甲烷浓度增加。同时为了探究分子扩散系数与膨胀扩散系数对于整体的影响程度，利用把分子扩散系数与膨胀扩散系数分别缩小1/2的方法来探究两者影响的大小。研究结果表明，当仅把分子扩散系数缩小1/2时，在5年和10年时，整体浓度上升13.8%和33%；当仅把膨胀扩散系数缩小两倍时，在5年和10年时，整体浓度上升4.2%和3.3%。所以，分子扩散系数在任何时刻占有主要影响，膨胀扩散系数的大小对开采初期影响较大，这与3.2.1节得出结论一致。
4 结论与认识
本文在原有模型的基础上增加了解吸项，并在运动方程中考虑了气体在致密砂岩气藏流动过程中碰撞滑移现象，使模型可以描述气体在致密砂岩储层中的流动规律。通过理论分析和数值模拟研究，并经过岩心仿真模拟与物理实验的对比，验证了考虑压力扩散项的模型比常规扩散渗流模型更准确。以中深层、深层及超深层气藏为背景，通过求解模型方程进行开采浓度及产量影响因素的数值模拟，并分析得出如下结论和认识：
（1）压力引起的膨胀扩散会使地层内部天然气的扩散量增加，产量增大。主要表现在天然气开采的初期和近井地带的浓度分布的影响较大，开采5年以内或距离井筒距离1 000 m以内，影响程度超过10%。
（2）在一定开采时间下，压力引起的膨胀扩散对于深层气藏和低渗气藏浓度分布影响较大，主要对于深度大于2 000 m（中深层以上）或地层渗透率小于1×10-3 μm2时，影响较大，可达10%以上，此时要考虑膨胀扩散系数对于地层甲烷浓度分布的影响。故对高压致密砂岩气藏对于压力引起的膨胀扩散不可忽略。
（3）在一定开采时间与地层原始压力下，降低井底流压会使天然气地层甲烷浓度降低，天然气产量增加，当井底流压由22 MPa下降至19 MPa时，近井地带浓度下降接近30%，而远井地带浓度下降只有8%，这说明降低井底流压并不能把距离井筒较远的天然气开采出来，所以在井距较远的情况下，用降低井底流压的方式增产效果较差。
（4）分子扩散和压力引起的膨胀扩散对天然气开采均有影响，分子扩散系数与膨胀扩散系数越大，扩散现象越剧烈，分子扩散对开采全程都占据主要影响。
甘公网安备 62010202000678号
