Establishment and application of a new water saturation model for shallow and loose fine-grained hydrate reservoirs

Jun ZHAO; Wenhai LIAO; Di TANG; Jiang JIA; Yuhu LUO

doi:10.11764/j.issn.1672-1926.2024.08.006

Natural Gas Geoscience >

2025 , Vol. 36 >Issue 2: 197 - 208

DOI: https://doi.org/10.11764/j.issn.1672-1926.2024.08.006

Establishment and application of a new water saturation model for shallow and loose fine-grained hydrate reservoirs

Jun ZHAO ^,¹ ,
Wenhai LIAO ¹ ,
Di TANG ² ,
Jiang JIA ¹ ,
Yuhu LUO ²

Expand

^1. School of Geoscience and Technology，Southwest Petroleum University，Chengdu 610500，China
^2. Hainan Branch，CNOOC （China） Co. ，Ltd. ，Haikou 570311，China

Received date: 2024-04-29

Revised date: 2024-08-08

Online published: 2024-09-30

Fold

Abstract

Water saturation is an important parameter in the evaluation of natural gas hydrate resources， but the accuracy of calculating water saturation using the traditional Archie formula is often unable to meet the requirements. According to the actual drilling and coring sediment data from Qiongdongnan Basin， six sediment samples with varying proportions were artificially prepared. The petroelectrical data during the hydrate formation of unconsolidated sediments were measured by petrophysical experiments， and the changing rules of resistivity and resistivity increasing coefficient were analyzed. The experimental results show that there is an exponential relationship between water saturation and resistivity increase coefficient of hydrate samples. Combined with digital core conduction simulation， an exponential water saturation calculation model is established. The exponential water saturation calculation model is more accurate than the traditional Archie formula when processing actual logging data. The exponential water saturation model provides a new method for evaluating natural gas hydrate resources.

Key words： Natural gas hydrate; Unconsolidated sediment; Logging response; Petroelectric characteristics; SaturationFundaion items：The CNOOC Special Project （Grant No. CEL202HNFN0009）; the Marine Economy Development Special Fund Project of Guangdong Province， China （Grant No. Guangdong Natural Resources ［2021］57）

Cite this article

Jun ZHAO , Wenhai LIAO , Di TANG , Jiang JIA , Yuhu LUO . Establishment and application of a new water saturation model for shallow and loose fine-grained hydrate reservoirs[J]. Natural Gas Geoscience, 2025 , 36(2) : 197 -208 . DOI: 10.11764/j.issn.1672-1926.2024.08.006

0 引言

在低温高压状态下，轻质烃被包裹在水分子中，形成一种似冰状固体化合物，称为天然气水合物。天然气水合物因其分布范围广、资源量巨大，燃烧清洁等优点，被认为是一类开发潜力巨大的非常规天然气资源^［1］，对保障我国能源安全具有重要意义。中国地质调查局现已探明南海浅层天然气水合物资源量巨大，特别是在东沙海域以及琼东南盆地等区域，有关水合物的勘探已取得突破。

天然气水合物通常被视为绝缘体，因此电阻率对含水合物储层的敏感度很高^［2］。电阻率法作为储层测井响应特征方法之一，与其他勘测方法相比，不仅可以确定水合物赋存位置，还能够探测水合物的成核、生成、饱和度以及含水量大小^［3］。目前，电阻率测井法在天然气水合物饱和度评价领域得到广泛应用。基于电阻率测井的饱和度解释模型主要采用阿尔奇公式^［4］，其可靠性取决于经验参数a、b、m和n的取值，传统阿尔奇公式在计算天然气水合物饱和度时更多地依赖于固定的m和n值，对不同形成条件下m、n的影响因素分析较少^［5］。王秀娟等^［6］利用阿尔奇公式计算了水合物饱和度，并对岩电参数取不同数值时出现的计算误差进行了讨论。陈玉凤等^［7］，陆敬宇等^［8］，LU等^［9-10］通过实验研究，发现水合物饱和度与电阻率之间并不遵循阿尔奇公式所描述的直线关系。ZHAO等^［11］结合X射线断层扫描和电阻率测量技术，推导了含水合物沉积物的三维空间结构和电阻率，提出阿尔奇定律饱和度指数与孔隙水迂曲度之间的新的对数关系来计算饱和度。赵军等^［12］分析了非成岩水合物沉积物的岩电关系，并利用逾渗网络对其导电机理模拟，在此基础上对阿尔奇公式进行修正。综上所述，前人在水合物岩电参数的研究方面，只是根据相关实验发现了非阿尔奇现象，但并未深入探讨其规律性；对于水合物饱和度的计算，先前的研究大多依赖传统的阿尔奇公式或基于实验对岩电参数进行修正，而缺乏提出符合岩电规律的全新饱和度模型。

本文采用电阻率为测量手段，在实验室条件下模拟天然气水合物的生成。通过对实时测量的岩电数据进行分析与处理，提出指数型阿尔奇公式用于海域深水浅层天然气水合物储层饱和度的计算（浅层指水合物储层埋深较浅，介于海底以下几十米至300 m内^［13］），并与传统阿尔奇公式计算结果进行对比，饱和度的计算精度得到了明显的提高。指数型阿尔奇公式为天然气水合物储层饱和度测井评价提供了一条新途径。

1 岩电实验

1.1　岩样制备及过程

根据收集到的琼东南盆地陵水靶区LS-A井海底10~50 m地层岩样，进行X射线衍射分析（XRD），得到地层矿物成分组成情况，其中石英含量为48%~61%，平均为53.69%；长石含量为9%~18%，平均为15.42%；黏土矿物含量为18%~26%，平均为22%；碳酸盐矿物含量为5%~13%，平均为8.69%；角闪石含量为1%~3%，平均为1.75%。由于实验条件的限制，只考虑了石英和黏土矿物2种矿物组分，利用矿物粉末人工配比制样。根据样品配比计算出样品的骨架密度，在套筒内体积已知的情况下，通过测量样品干重估算其孔隙度。基于这些条件，制备出6个沉积物样品（表1）。

表1 岩电实验岩样配比

Table 1 Rock sample ratio of rock electrical experiment

样品	石英砂	绿泥石	孔隙度/%
样品1	100%（150 μm）	/	40.18
样品2	100%（1 000 μm）	/	42.56
样品3	100%（75 μm）	/	38.89
样品4	90%（500 μm）	10%	31.84
样品5	80%（500 μm）	20%	29.76
样品6	75%（500 μm）	25%	30.89

注：“/”代表无数据

实验过程分为以下6个步骤：①使用预先配置的盐水对岩样进行饱和处理，装入高压反应釜内，并在岩样底部出水口位置放置过滤网，以防止砂砾堵塞仪器；②打开围压加压阀，设置围压为8 MPa，然后打开甲烷气瓶以及天然气注入阀，向高压反应釜中注入天然气，直到孔压略高于围压；③等待1~2 h，使孔压稳定，确保夹持器内部没有气体泄漏，记录此时的电阻率；④启动低温循环制冷水槽，设定水槽温度为2 ℃，开启制冷循环，同时打开数据记录模块，实时记录水合物生成过程中岩电参数的变化；⑤随着实验进行，观察到电阻率和孔压在一段时间内稳定下来，表明岩样中的天然气已经消耗完毕，此时认为反应达到平衡状态，记录平衡状态下的电阻率，然后再次注入天然气，继续生成天然气水合物；⑥记录和处理实验数据，计算水合物的饱和度。

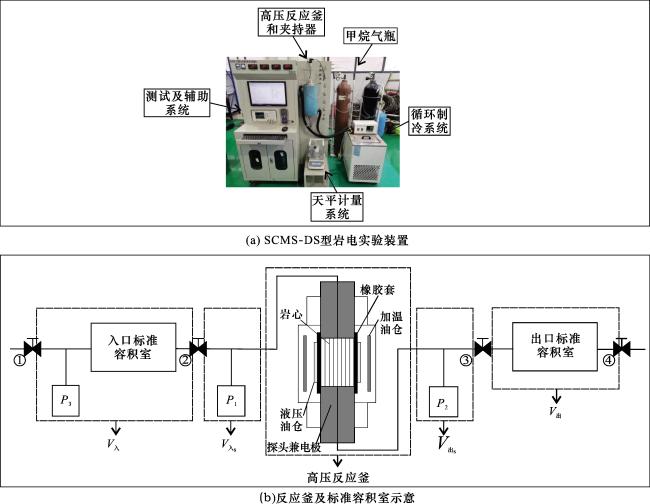
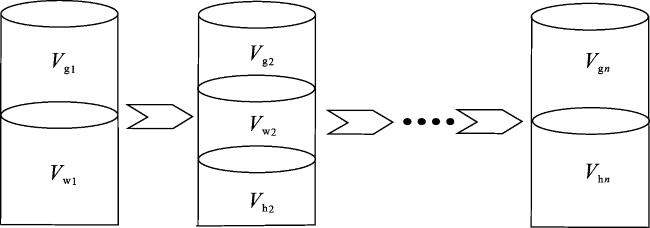
1.2　实验过程及饱和度确定

实验通过向装置高压反应釜内持续分阶段供给天然气的方法来合成水合物^［14］。向饱含水的岩样中充入天然气，驱出一定量的水，为水合物创造生成空间，分阶段持续向岩样中注入天然气，水合物会在适当的条件下生成，计算平衡时的含水饱和度及水合物饱和度。

装置中标准容积室和管线的体积对计算结果有较大的影响，需对入口、出口标准容积室的体积

V 入

、

V 出

及其管线体积

V 入 s

、

V 出 s

进行标定，装置概况如图1所示。

显示原图|下载原图ZIP|生成PPT

图1 岩电实验装置概况

Fig.1 General diagram of rock electrical experimental equipment

标准容积室体积和管线体积的标定方法如下所述：

在高压反应釜中装入实心不锈钢模块，注入一定压力的天然气，关闭阀门②，打开阀门①放空入口标准容积室内气体

V 1

，记录初始稳定压力为

P 入 1, a

；关闭阀门①，打开阀门②，记录稳定状态压力为

P 入 1, b

。建立P-V-T平衡状态方程：

P 入 1, a V 入 s Z 入 1, a = P 入 1, a V 入 s + V 入 Z 入 1, a

(1)

式中：

P 入 1, a

为初始稳定状态压力，MPa；

P 入 1, b

为稳定状态压力，MPa；

V 入

为入口标准容积室体积，cm³；

V 入 s

为入口管线体积，cm³；

Z 入 1, a

为压力在

P 入 1, a

条件下天然气的压缩因子；

Z 入 1, b

为压力在

P 入 1, b

条件下天然气的压缩因子。

往标准容积室内装入已知体积

V 2

的模块，重复上述步骤，记录阀门②关闭和打开时的压力分别为

P 入 2, a

和

P 入 2, b

。建立P-V-T平衡状态方程：

P 入 2, a V 入 s Z 入 2, a = P 入 2, b V 入 s + V 入- V 2 Z 入 2, b

(2)

不断更换标准容积室内的模块体积，重复上述过程，可以得到多个恒温状态下的P-V-T平衡状态方程：

P 入 n, a V 入 s Z 入 n, a = P 入 n, b V 入 s + V 入- V n Z 入 n, b

(3)

式中：

V n

为第n个模块的体积，cm³，i=1，2，3，…，n，且

V 1

=0。

根据上述方程建立方程组，即可求得入口标准容积室

V 入

及入口管线体积

V 入 s

。

对出口标准容积室

V 出

及出口管线体积

V 出 S

的标定采取与公式（1）、式（2）相同步骤，得到多个恒温状态下的P—V—T平衡状态方程：

P 出 n, a V 入 s Z 出 n, a = P 出 n, b V 出 S + V 出 - V n Z 出 n, b

(4)

即可求得出口标准容积室

V 出

及出口管线体积

V 出 s

。

水合物生成过程如图2中所示，用

V g i

、

V w i

和

V h i

分别表示为第i次充气时，反应釜内天然气、水以及生成水合物的体积。结合物质平衡方程和P—V—T状态方程，根据实验测试条件，建立计算实验过程中水合物饱和度的模型。

显示原图|下载原图ZIP|生成PPT

图2 反应釜内水合物生成过程

Fig.2 Hydrate formation process in reactor

第一次水合物的生成过程：

反应初始，釜中的压力为

P 1, a

，相应的压缩因子为

Z 1, a

，这时，在该体系中，物质的量为

n 1, a

的天然气充满反应釜空间

V g 1

以及管线体积

V 入 s

，可以建立P—V—T平衡状态方程：

P 1, a V g 1 + V 入 s = Z 1, a n 1, a R T

(5)

式中：

V g 1

为第一次加入天然气时釜内的天然气体积，cm³；

n 1, a

为第一次加入天然气的物质的量，mol；

R

为阿伏伽德罗常数，1/mol；

T

为温度，℃。

当反应完成时，釜内的压力为

P 1, b

，相应的压缩因子为

Z 1, b

，此时，天然气物质的量为

n 1, b

，充满反应釜内空间

V g 2

和管线体积

V 入 s

，此时：

P 1, b V g 2 + V 入 s = Z 1, b n 1, b R T

(6)

式中：

P 1, b

为第一次反应结束时釜内压力，MPa；

V g 2

为反应结束时釜内的天然气体积，cm³；

Z 1, b

为釜内压力为

P 1, b

时对应的压缩因子；

n 1, b

表示反应结束时釜内天然气的物质的量，mol。

首次合成天然气水合物消耗天然气物质的量是：

Δ n 1 = n 1, a - n 1, b = P 1, a V g 1 + V 入 s Z 1, a n 1, a R T - P 1, b V g 2 + V 入 s Z 1, b n 1, b R T

(7)

式中：

Δ n 1

表示第一次反应消耗的天然气的物质的量，mol。

通过首次排放的水的质量可以获得反应釜内的天然气体积

V g 1

，而

V g 2

则需通过下列步骤来得到：

将物质的量为

n 3

的天然气充入入口标准容积室

V 入

中，其稳定压力为

P 3

，相应的压缩因子为

Z 3

，建立P-V-T平衡状态方程：

P 3 V 入 = Z 3 n 3 R T

(8)

式中：

P 3

表示再次充入天然气后稳定状态压力，MPa；

Z 3

表示稳定状态对应的压缩因子；

n 3

表示再次向容积室中充入的天然气的物质的量，mol。

然后打开容积室的入口阀门，使天然气扩散至反应釜内，气体快速膨胀，达到平衡，压力变为

P 2, a

，相应的压缩因子为

Z 2, a

，此时的平衡状态方程：

P 2, a V g 2 + V 入 s + V 入 = Z 2, a n 1, b + n 3 R T

(9)

综合上述两式可以得到

V g 2

表达式：

V g 2 = P 2, a V 入 s + V 入 Z 2, a - P 1, b V 入 s Z 1, b - P 3 V 入 Z 3 P 1, b Z 1, b - P 2, a Z 2, a

(10)

由上述公式得到天然气的消耗量

Δ n 1

，根据天然气水合物生成的反应方程式来计算出消耗

Δ n 1

天然气时相应的水消耗量，用体积表示为

Δ V w 1

。反应釜中剩余水体积为：

V w 2 = V w 1 - Δ V w 1

(11)

式中：

V w 1

表示第一次反应前釜内水的体积，cm³；

V w 2

表示第一次反应后釜内水的体积，cm³；

Δ V w 1

表示消耗

Δ n 1

天然气时相应的水消耗量，cm³。

第一次天然气水合物生成结束时，多孔介质的含水饱和度为：

S W = V w 2 V φ

(12)

式中：

S w

表示第一次反应结束时多孔介质的含水饱和度，%；

V φ

表示釜内孔隙体积，cm³。

水合物饱和度表示为：

S h = V h 2 V φ = V φ - V w 2 V φ

(13)

式中：

S h

表示第一次反应结束时多孔介质的水合物饱和度，%；

V h 2

表示第一次反应生成的水合物的体积，cm³。

根据上述步骤，得到每一次水合物生成完毕时人工制备岩样中的含水饱和度和水合物饱和度。

在岩心样品夹持器中，样品的电阻采用二极法进行测量。上下电极被连接到电桥仪测量得到样品的电阻，再由欧姆定律计算得到样品的电阻率：

R = r S L

(14)

式中：

R

为样品电阻率，Ω·m；

r

为样品电阻，Ω；

S

为样品横截面积，m²；

L

为样品长度，m。

表2、表3所示，为此次岩电实验的水合物岩样在不同水合物饱和度条件下得到的电阻率（R）以及电阻率增大系数（I）。其中，电阻率增大系数为储层电阻率与储层全含水的电阻率的比值^［15］。

表2 不同粒径大小水合物岩样岩电实验数据

Table 2 Electrical experimental data of hydrate samples with different particle sizes

加气次数	粒径1 000 μm				粒径150 μm			粒径75 μm
加气次数	$S h$		R/（Ω·m）	I	$S h$	R/（Ω·m）	I	$S h$	R/（Ω·m）	I
1	0.12	2.43		0.65	0.06	0.81	0.98	0.05	1.62	1.14
2	0.34	6.88		2.44	0.13	1.21	1.30	0.17	2.43	1.46
3	0.41	13.36		4.72	0.29	3.64	2.76	0.27	7.69	4.72
4	0.61	40.49		14.47	0.38	8.09	5.69	0.41	12.96	7.80
5	0.77	96.36		34.47	0.49	14.17	9.59	0.54	21.46	13.33
6	/	/		/	0.59	31.98	20.98	0.70	49.39	30.57

注：“/”表示无数据

表3 不同泥质含量水合物岩样岩电实验数据

Table 3 Electrical experimental data of hydrate samples with different shaliness content

加气次数	泥质含量10%			泥质含量20%			泥质含量25%
加气次数	$S h$	R/（Ω·m）	I	$S h$	R/（Ω·m）	I	$S h$	R/（Ω·m）	I
1	0.12	4.80	3.00	0.09	2.29	2.43	0.10	2.07	1.29
2	0.22	7.64	4.78	0.16	3.82	3.39	0.19	2.95	1.84
3	0.36	8.29	5.19	0.37	6.99	4.37	0.28	4.04	2.52
4	0.45	13.54	8.46	0.46	10.69	6.69	0.35	4.80	3.00
5	0.57	16.38	9.24	0.56	12.77	7.98	0.46	7.31	4.57
6	/	/	/	0.68	15.28	9.55	0.66	10.26	7.81
7	/	/	/	0.73	17.90	13.19	/	/	/

注：“/”表示无数据

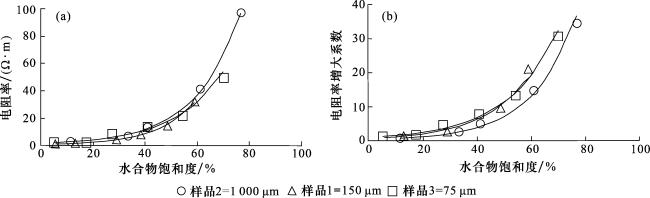
1.3　实验数据分析

不同粒径的岩样实验计算所得水合物饱和度与电阻率以及电阻率增大系数之间的关系，如图3所示，电阻率以及电阻率增大系数与水合物饱和度间均呈指数正相关。通过观察发现岩样电阻率随水合物饱和度的增加而增大，前期增长速度较缓慢，而在水合物饱和度达到60%后，电阻率开始迅速增大。

显示原图|下载原图ZIP|生成PPT

图3 不同粒径水合物沉积物的电阻率和电阻率增大系数与水合物饱和度的关系

（a）电阻率与水合物饱和度关系；（b）电阻率增大系数与水合物饱和度关系

Fig.3 Relation between resistivity and resistivity increase coefficient of hydrate deposits with different particle sizes and hydrate saturation

分析原因，一方面是由于水合物的填充效应，其生成过程中会填充沉积物中的孔隙空间。初始阶段，水合物可能填充一些较大的孔隙，对电阻率的增加影响较小。随着饱和度的提高，水合物开始填充更多的微小孔隙和孔隙连接处，这些孔隙通常是电子传导路径，因此当它们被填充会显著增加电阻率。另一方面，初始阶段水合物含量比较少，生成速率缓慢，由于沉积物中含有盐溶液，排盐效应占据主导地位，排盐效应导致电阻率降低。水合物饱和度达到60%后，水合物生成速率提高，排盐效应造成的影响相对减弱，具有滞后效应，电阻率增大速率变快^［16］。前人也通过电阻层析成像测试发现电阻率随水合物饱和度的变化并不是线性增加的，而是呈非线性增大趋势^［17］。

不同泥质含量的岩样实验计算所得水合物饱和度与电阻率以及电阻率增大系数也均呈指数正相关，如图4所示，沉积物的电阻率随泥质含量的增加而降低。比较不同泥质含量沉积物的电阻率变化曲线，显然泥质含量越高的沉积物电阻率和电阻率增大系数都更低。分析其原因，泥质含量增加会使得颗粒之间的连通路径更多，电流能够更容易地在颗粒之间通过，提高了电导性，使得电阻率降低；另外，泥质颗粒表面可能会带有电荷，并能够吸附溶解的离子，这些吸附的离子增加了电导性，也会导致电阻率的降低。前人通过对泥质砂岩水合物储层的电阻率进行数值模拟，同样发现随泥质含量的增加，水合物储层的电阻率总体上是减小的^［18］。

显示原图|下载原图ZIP|生成PPT

图4 不同泥质含量水合物沉积物的电阻率和电阻率增大系数(a)与水合物饱和度关系(b)

（a）电阻率与水合物饱和度关系；（b）电阻率增大系数与水合物饱和度关系

Fig.4 Relation between resistivity and resistivity increasing coefficient of hydrate deposits with different muddy content and hydrate saturation

根据收集到的研究区岩心组成资料，目前开展的实验只是针对富含泥质细粒沉积物岩电响应规律的探讨，对其他地区富砂型沉积物不一定适用。富含泥质细粒沉积物的孔隙结构通常较为复杂，颗粒之间接触面积大，电导率相对较高；而富砂型沉积物的孔隙结构更为开放，颗粒之间的空隙较大，虽然电子传导路径可能更直接，但由于缺乏导电物质，电导率通常较低。富砂型沉积物的电阻率响应可能更加敏感于孔隙结构的变化，而不是泥质含量的改变。

2 饱和度模型的建立

2.1　实验分析岩电规律

地球物理测井中，电阻率是受到天然气水合物影响最为显著的特征之一。因此，高电阻率异常可作为识别天然气水合物稳定区域的重要指标^［19］。在电阻率计算饱和度的方法中，广泛采用阿尔奇公式建立地层电阻率与孔隙流体饱和度之间的经验关系：

S w = a b R w R t φ m 1 n

(15)

式中：

R t

为饱和水电阻率，Ω·m；

R w

为地层水电阻率，Ω·m；

S w

为含水饱和度，%；

φ

为孔隙度，%；

a

为比例系数；

b

为岩性系数；

m

为胶结系数；

n

为饱和度指数。

根据上述实验测得的含水饱和度和电阻率增大系数以及样品的孔隙度与地层因素，建立它们之间的关系，如图5所示。其中，地层因素定义为100%水饱和的沉积物的电阻率与孔隙水电阻率之比^［20］，图5（a）展示了孔隙度与地层因素的关系，岩样地层因素与孔隙度的关系与岩样孔隙中流体类型无关，因此，含水合物样品的地层因素与孔隙度之间遵循阿尔奇规律；图5（b）展示了样品电阻率增大系数和含水饱和度的关系。在双对数坐标下，含水合物样品的含水饱和度和电阻率增大系数之间呈现出指数关系，不符合阿尔奇规律。

显示原图|下载原图ZIP|生成PPT

图5 水合物岩样地层因素—孔隙度关系与电阻率增大系数—含水饱和度关系

Fig.5 The relationship between formation factor-porosity and resistivity increase factor-water saturation of hydrate samples

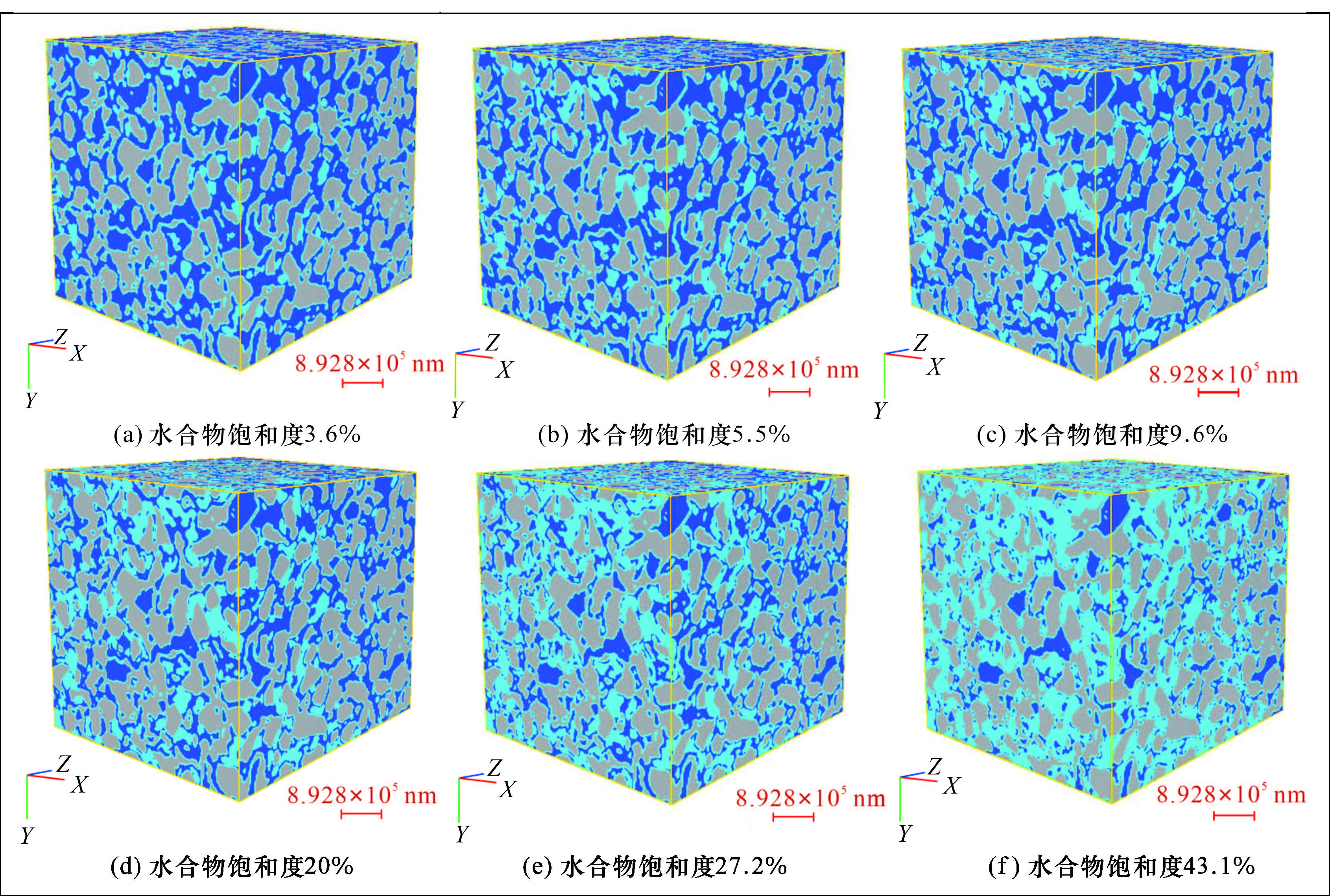
2.2　岩电规律的数值模拟

随着计算机技术的发展，数字岩心技术在地质科学和能源领域得到了广泛应用^［21-23］。利用数字岩心技术，能获取到天然气水合物岩心的微观结构和特征^［24-25］，进而开展基于岩心的模拟研究。为验证根据岩电实验得到的水合物岩样含水饱和度与电阻率增大系数之间指数型关系的合理性，建立数字岩心对水合物岩样进行导电模拟。

水合物CT实验采用的多孔介质为500 μm粒径的石英砂，生成水合物所需的气体选用高纯氙气替代甲烷气体，因为甲烷气和甲烷水合物的造影效果较差，利用甲烷气形成水合物进行CT扫描实验，难以对样品孔隙中的流体分布进行准确的刻画，液体选用质量浓度为3.6%碘化钾盐水。基于X射线CT扫描人造天然气水合物岩心的二维切片数据，利用图像叠加技术建立三维数字岩心模型。对岩心所有平面的二维灰度图进行阈值分割，选择合适的阈值将灰度图转化为二值图，由于水合物岩心中包含骨架、盐水和水合物3个部分，设置2个阈值L1和L2做2次分割。把所有的二值图叠加起来，将二维图像组合成三维数字岩心模型（图6）。

显示原图|下载原图ZIP|生成PPT

图6 三维数字岩心模型（骨架和水合物两相）

Fig.6 3D digital core model （skeleton and hydrate two-phase）

对岩心中不同部分重新上色，灰色部分为骨架，浅蓝部分为水合物，深蓝部分为盐水；对水合物生长过程中不同时间测得的CT扫描数据重构三维模型，计算每一个三维模型对应的水合物饱和度，如图7所示。

显示原图|下载原图ZIP|生成PPT

图7 水合物岩样在不同水合物饱和度条件下对应的三维模型

Fig.7 Corresponding 3D models of hydrate samples under different hydrate saturation conditions

利用有限元理论求解数字岩心的有效电阻率。对岩心施加外加电场，确定每个体素上的电势分布，结合变分原理，将电势分布转化为系统能量极值问题进行求解：

∂ E n ∂ u m = 0

(16)

式中：

E n

为系统能量，J；

u m

为节点电势，V。

对每一个体素而言，其8个顶点与相邻体素连接，建立每个单元上的有限元方程。为实现三维数字岩心有限元模拟，定义变量：单元内第r个节点处电势u _r，单元的电导率张量s _pq，外部电场矢量E，单元内部电场e，刚度矩阵D _rs，单元形状数组N _r，其中r和s为单元节点，p和q为坐标系。

对任一单元，设其内电势可表示为V（x，y，z），其中0<x，y，z<1，易知，V可表示为单元节点上电势的函数，即：

V x, y, z = N r x, y, z u r

(17)

单元内部电场可表示为电势的梯度，即：

e p x, y, z = - ∂ V x, y, z ∂ x p = - ∂ N r ∂ x p u r

(18)

对于任一单元内的能量为：

E n = ∫ 0 - 1 ∫ 0 - 1 ∫ 0 - 1 d x d y d z 12 e p σ p q e q = 12 u r ∫ 0 - 1 ∫ 0 - 1 ∫ 0 - 1 d x d y d z n p r T σ p q n q s u s

(19)

上式可通过Simpson公式计算，式中

D r s = ∫ 01 ∫ 01 ∫ 01 d x d y d z n p r T σ p q n q s

为8×8的刚度矩阵，单元内能量可进一步表示为：

E n = 12 u r D r s u s

(20)

根据上述导电模拟方法，利用COMSOL软件模拟不同含水饱和度状态下对应的数字岩心在X、Y、Z 3个方向上的电阻率增大系数和含水饱和度的关系。参考相关文献^［26］，确定数字岩心各组分的电导率，多孔介质骨架成分为石英砂，电导率非常低，不易传导电流，取值范围在10^-16~10^-8S/m之间；水合物则是一种在低温高压条件下形成的结晶物质，主要由天然气分子和水构成，其中天然气部分是非导电的气体分子，而水在这种结晶状态下的电导率也相对较低，取值在10^-6S/m左右；孔隙水取值范围在2.85~5 S/m之间。本文中设置孔隙水的电导率为4 S/m、水合物的电导率为2×10^-4 S/m、骨架的电导率为10^-14S/m（表4），进而便可求得整个数字岩心的有效电导率。

表4 数字岩心各组分电性参数

Table 4 Electrical parameters of each component of digital core

岩样组分	电导率/（S/m）	电阻率/（Ω·m）
石英砂骨架	10^-14	1×10¹⁴
水合物	2×10^-4	5×10³
孔隙水	4	2.5×10^-1

利用不同水合物饱和度条件下的CT扫描数据建立数字岩心，通过数值模拟得到不同水合物饱和度条件下样品的电阻率，模拟结果如图8所示。分析含水合物样品的岩电规律，与岩电实验规律一致，电阻增大系数与含水饱和度之间呈现明显的指数关系。

显示原图|下载原图ZIP|生成PPT

图8 水合物数字岩心在3个方向上的电阻增大系数与含水饱和度的关系

Fig.8 Relation between resistance increase coefficient and water saturation of hydrate digital core in three directions

2.3　饱和度模型的建立

根据岩电实验以及数字岩心模拟结果，含水合物样品的含水饱和度和电阻率增大系数之间不再符合阿尔奇规律，二者之间的关系更符合指数关系：

I = b × e n S w

(21)

式中：

I

为电阻率增大系数；

S w

为含水饱和度，%；

n

为指数系数；

b

为岩性系数。

而含水合物样品的地层因素和孔隙度之间依然符合阿尔奇公式规律：

F = a φ m

(22)

式中：

F

为地层因素；

φ

为孔隙度，%；

m

为胶结系数；

a

为比例系数。

结合上述两式可以建立指数型阿尔奇公式：

S w = L n a b R w R t φ m n

(23)

式中：

S w

为含水饱和度，%；

R w

为地层水电阻率，Ω·m；

R t

为饱和水电阻率，Ω·m；

φ

为孔隙度，%；

n

为指数型阿尔奇系数。

根据前述实验拟合得到适合于本地区的岩电参数a、b、m以及n的取值，具体为a取1.05，m取2.34，b取9.13，n取2.20。于是，建立出本研究区水合物饱和度计算的指数型阿尔奇公式如下：

S h = 1 - S w = 1 - L n 9.59 R w R t φ 2.34 2.2

(24)

式中：

S h

为水合物饱和度，%；

S w

为含水饱和度，%；

R w

为地层水电阻率，Ω·m；

R t

为饱和水电阻率，Ω·m；

φ

为孔隙度，%。

3 应用及效果分析

为验证本文提出式（24）在实际应用中的效果，对琼东南盆地的X井和Y井水合物层段进行了不同饱和度模型下的计算结果对比（图9，图10）。琼东南盆地位于中国南海北部，整体呈NE—SE走向。盆地北邻海南岛，西邻莺歌海盆地，东邻珠江口盆地，南邻西沙隆起^［27-28］，由4个一级构造单元组成，包括北部坳陷带、北部隆起带、中央坳陷带和南部隆起带。琼东南盆地是继神狐海域和东沙海域之后，在南海北部发现天然气水合物的新领域，也是重要的天然气水合物勘探远景区^［29-31］，具有巨大的水合物资源潜力。

显示原图|下载原图ZIP|生成PPT

图9 X井饱和度解释成果

Fig.9 X Well saturation interpretation results

显示原图|下载原图ZIP|生成PPT

图10 Y井饱和度解释成果

Fig.10 Y Well saturation interpretation results

图9中的130~170 m和图10中的205~265 m水合物储集层段与正常地层在常规测井曲线上呈现出明显的差异。具体表现在：电阻率曲线上，富集水合物层段的电阻率相对于上下围岩段显著增加；声波时差曲线上，水合物取代原有含水孔隙导致声波速度增大、时差减小；自然伽马曲线呈现低值；井径测井响应出现扩径现象；密度曲线上，由于储集空间被水合物填充后，孔隙中海水和泥质减少，总体略微降低。

利用传统阿尔奇公式、指数型阿尔奇公式分别计算了X、Y 2口井水合物储层饱和度。采用岩心孔隙水氯离子浓度计算的天然气水合物饱和度作为实际测量值，用来评估饱和度模型的预测效果，因为氯离子在海洋沉积物孔隙中含量丰富且性质稳定，受到的控制因素较少、计算精度高，可被视为真饱和度^［32］。根据2种模型计算饱和度的变化趋势对比可以看出，本文提出的指数型阿尔奇公式处理得到的水合物饱和度相比于传统阿尔奇公式的计算结果，与岩心饱和度最接近。

从表5中不同饱和度模型计算结果误差也能够看出，利用指数型阿尔奇公式计算水合物饱和度的误差是小于传统阿尔奇公式计算的。同时结合黏土矿物含量为20%和25%的2块样品岩电实验结果和实测电阻率，得到不同深度对应的实验饱和度。与实验饱和度比较同样也表明指数型阿尔奇公式计算效果更好，此方法有效提高了电阻率计算水合物饱和度的准确度。

表5 不同模型饱和度计算误差对比

Table 5 Comparison of saturation calculation errors of different models

井号	深度 /m	岩心饱和度	传统阿尔奇	相对误差 /%	指数阿尔奇	相对误差 /%
X	135.69	0.14	0.39	178.00	0.22	55.26
	136.39	0.17	0.39	128.72	0.31	80.88
	137.17	0.23	0.38	64.29	0.20	13.64
	139.30	0.11	0.40	263.30	0.30	170.02
	140.82	0.19	0.37	94.97	0.28	49.71
	149.06	0.14	0.30	113.39	0.18	25.03
	150.61	0.13	0.33	151.23	0.19	42.55
	151.67	0.25	0.34	37.35	0.18	27.57
平均相对误差				128.91		58.08
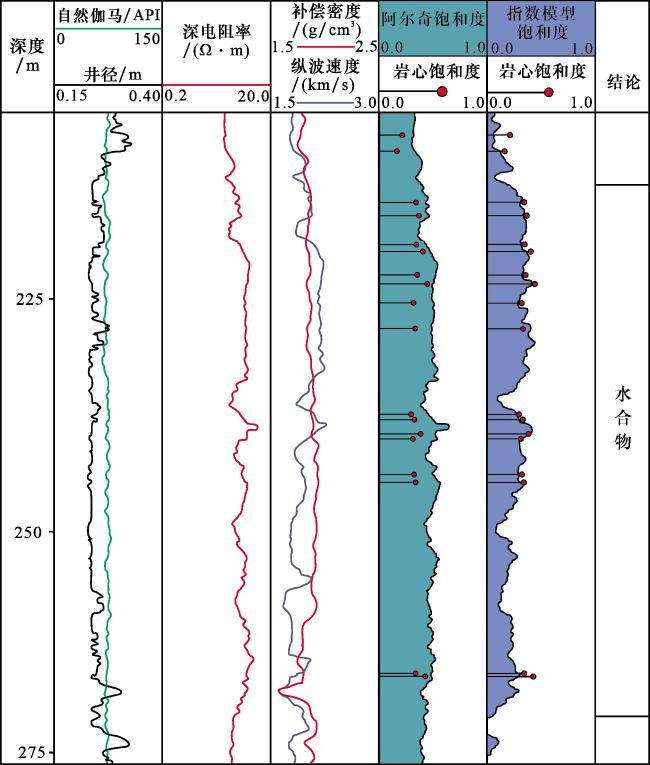
Y	209.14	0.15	0.32	121.7	0.10	30.28
	214.63	0.33	0.45	30.62	0.31	3.80
	216.07	0.35	0.42	31.39	0.35	0.10
	217.31	0.37	0.46	1.71	0.36	1.94
	219.15	0.33	0.36	32.1	0.32	3.41
	219.91	0.39	0.44	21.92	0.36	8.06
	222.43	0.34	0.47	54.45	0.33	1.66
	223.37	0.43	0.49	15.03	0.42	1.10
平均相对误差				38.61		6.29

4 结论

（1）分析了不同粒径大小、不同泥质含量水合物岩样的饱和度与电阻率的变化规律。随着水合物含量的增加，电阻率前期平缓增长，当水合物饱和度达到一定程度后迅速增加，呈现非线性增长关系，天然气水合物饱和度与电阻率增大系数间呈指数正相关关系；含水饱和度与电阻率增大系数之间不符合阿尔奇规律，在双对数坐标下符合指数变化关系。

（2）数值模拟的结果表明，电阻率增大系数与含水饱和度之间也呈现明显的指数变化规律，数字岩心的模拟结果与实验分析结果一致，验证了含水饱和度和电阻率增大系数之间呈指数型规律的合理性。

（3）利用指数型阿尔奇公式，对琼东南盆地X井和Y井水合物层饱和度进行计算，并与传统阿尔奇公式进行对比，指数型阿尔奇公式所计算的水合物饱和度相对于传统阿尔奇计算误差更小，新模型能够提高水合物储层饱和度的精度，能够满足现场对饱和度计算精度的需求。

References

Publishing order | Descend order by publishing year | Descend order by cited within

1	李丽松，苗琦.天然气水合物勘探开发技术发展综述［J］.天然气与石油，2014，32（1）：67-71，11-12. LI L S， MIAO Q. A review on the development of natural gas hydrate exploration and development technologies［J］.Natural Gas & Oil，2014，32（1）：67-71，11-12.

2	范宜仁，朱学娟.天然气水合物储层测井响应与评价方法综述［J］.测井技术，2011，35（2）：104-111. FAN Y R， ZHU X J. Review on logging response and evaluation methods of natural gas hydrate reservoirs［J］.Well Logging Technology，2011，35（2）：104-111.

3	陈玉凤，周雪冰，梁德青，等.沉积物中天然气水合物生成与分解过程的电阻率变化［J］.天然气地球科学，2018，29（11）：1672-1678. CHEN Y F， ZHOU X B， LIANG D Q， et al. Resistivity variation during formation and decomposition of natural gas hydrate in sediments［J］.Natural Gas Geoscience，2018，29（11）：1672-1678.

4	林振洲，孔广胜，潘和平，等.木里地区天然气水合物储层参数计算［J］.物探与化探，2017，41（6）：1099-1104. LIN Z Z， KONG G S， PAN H P， et al. Parameter calculation of gas hydrate reservoir in Muli area［J］. Geophysical and Geochemical Exploration，2017，41（6）：1099-1104.

5	王英梅，焦雯泽，刘生浩，等.含天然气水合物沉积物的电阻率特性及阿尔奇公式的应用进展［J］.物探与化探，2023，47（3）：782-793. WANG Y M，JIAO W Z，LIU S H，et al. Resistivity characteristics of natural gas hydrate deposits and application of Archie formula［J］.Geophysical and Geochemical Exploration，2023，47（3）：782-793.

6	王秀娟，吴时国，刘学伟，等.基于电阻率测井的天然气水合物饱和度估算及估算精度分析［J］.现代地质，2010，24（5）：993-999. WANG X J， WU S G， LIU X W， et al. Estimation and accuracy analysis of gas hydrate saturation based on resistivity logging［J］. Geoscience，2010，24（5）：993-999.

7	陈玉凤，李栋梁，梁德青，等.含天然气水合物的海底沉积物的电学特性实验［J］.地球物理学进展，2013，28（2）：1041-1047. CHEN Y F，LI D L，LIANG D Q，et al.Experimental study on electrical properties of seafloor sediments containing natural gas hydrates［J］. Progress in Geophysics，2013，28（2）：1041-1047.

8	陆敬安，杨胜雄，吴能友，等.南海神狐海域天然气水合物地球物理测井评价［J］.现代地质，2008，22（3）：447-451. LU J A， YANG S X， WU N Y， et al. Evaluation of gas hydrate geophysical logging in the Shenhu area of the South China Sea［J］. Geoscience，2008，22（3）：447-451.

9	LU H，KAWASAKI T，UKITA T，et al.Particle size effect on the saturation of methane hydrate in sediments：Constrained from experimental results［J］.Marine and Petroleum Geology，2010，28（10）：1801-1805.

10	LU S，MCMECHAN A G.Estimation of gas hydrate and free gas saturation，concentration，and distribution from seismic data［J］.Geophysics，2002，67（2）：582-593.

11	ZHAO J H，LIU C L，LI C F，et al.Pore-scale investigation of the electrical property and saturation exponent of Archie’s law in hydrate-bearing sediments［J］.Journal of Marine Science and Engineering，2022，10（1）：111.

12	赵军，师执峰，李元平，等.天然气水合物储层导电特性模拟与饱和度计算［J］.天然气地球科学，2021，32（9）：1261-1269. ZHAO J， SHI Z F， LI Y P， et al. Electrical conductivity simulation and saturation calculation of natural gas hydrate reservoirs［J］. Natural Gas Geoscience， 2021，32（9）：1261-1269.

13	周守为，陈伟，李清平，等.深水浅层非成岩天然气水合物固态流化试采技术研究及进展［J］.中国海上油气，2017，29（4）：1-8. ZHOU S W，CHEN W，LI Q P，et al.Research and progress on solid-state fluidization test of shallow non-lithified natural gas hydrates in deep waters［J］.China Offshore Oil and Gas，2017，29（4）： 1-8.

14	赵军，戢宇强，武延亮.利用声波资料计算天然气水合物饱和度的可靠性实验［J］.天然气工业，2017，37（12）：35-39. ZHAO J，JI Y Q，WU Y L.Reliability experiment for calculating gas hydrate saturation using acoustic wave data［J］.Natural Gas Industry，2017，37（12）：35-39.

闫琪，白明明，徐景林，等.计算含油气饱和度没有必要引入电阻增大率及其统计参数n和b［J］.中国石油和化工标准与质量，2022，42（1）：118-119.

YAN Q，BAI M M，XU J L，et al. It is not necessary to introduce the resistance increase rate and its statistical parameters n and b to calculate the oil and gas saturation［J］.China Petroleum and Chemical Standards and Quality，2022，42（1）：118-119.

16	徐卫平，丁拼搏，张峰，等.天然气水合物岩石物理实验研究进展［J］.石油物探，2023，62（6）：1016-1029. XU W P，DING P B，ZHANG F，et al. Progress of petrophysical experiments on natural gas hydrate［J］.Geophysical Prospecting for Petroleum，2023，62（6）：1016-1029.

17	李彦龙，孙海亮，孟庆国，等.沉积物中天然气水合物生成过程的二维电阻层析成像观测［J］.天然气工业，2019，39（10）：132-138. LI Y L，SUN H L，MENG Q G，et al. Two-dimensional resistance tomography observation of gas hydrate formation in sediments［J］.Natural Gas Industry，2019，39（10）：132-138.

胡旭东，邹长春，肖昆，等.泥质砂岩天然气水合物储层电阻率数值模拟［C］//中国地球科学联合学术年会论文集（十）—专题二十八：油藏地球物理、专题二十九：油气地球物理、专题三十：深地资源地震波勘探理论、方法进展. 中国地球物理学会， 2021： 288-289.

HU X D， ZOU C C， XIAO K， et al. Numerical simulation of Resistivity of shale sandstone gas hydrate reservoir［C］//Proceedings of the China Earth Science Joint Academic Annual Conference （10） - Special Topics 28： Reservoir Geophysics， Special Topics 29： Oil and Gas Geophysics， and Special Topics 30： Theoretical and methodological progress in deep earth resource seismic wave exploration. Chinese Geophysical Society， 2021： 288-289.

19	甘华阳，王家生，陈建文，等.海底天然气水合物的饱和度预测技术［J］.海相油气地质，2004，9（1）：111-115，121. GAN H Y， WANG J S， CHEN J W， et al. Saturation prediction technology of submarine gas hydrate［J］.Marine Origin Petroleum Geology，2004，9（1）：111-115，121.

20	陈玉凤，李栋梁，梁德青，等.南海沉积物天然气水合物饱和度与电阻率的关系［J］.石油学报，2013，34（3）：507-512. CHEN Y F，LI D L，LIANG D Q，et al. Relationship between gas hydrate saturation and resistivity in sediments in the South China Sea［J］.Acta Petrolei Sinica，2013，34（3）：507-512.

21	CHI P， SUN J M， LUO X， et al.Reconstruction of 3D digital rocks with controllable porosity using CVAE-GAN［J］.Geoenergy Science and Engineering，2023，230：212264.

22	GUBAIDULLIN M G，BELOZEROV I P.Digital core modeling technology for determining the reservoir-capacitive properties of terrigenous reservoirs［J］.IOP Conference Series（Materials Science and Engineering），2021，1201（1）：012065.

23	IGOR V，VLADIMIRR S，IVAN Y.3D multiclass digital core models via microCT，SEM-EDS and deep learning［J］.E3S Web of Conferences，2023，366：01003.

董怀民，孙建孟，林振洲，等.基于CT扫描的天然气水合物储层微观孔隙结构定量表征及特征分析［J］.中国石油大学学报（自然科学版），2018，42（6）：40-49.

DONG H M， SUN J M， LIN Z Z， et al. Quantitative characterization and characteristic analysis of micro-pore structure of gas hydrate reservoir based on CT scanning［J］.Journal of China University of Petroleum （Natural Science Edition），2018，42（6）：40-49.

25	LI S H， LI S，PANG W X.Description of gas hydrate using digital core technology［J］.Journal of Energy Resources Technology，2020，142（6）：062901.

26	陈玉凤，吴能友，梁德青，等.基于分形孔隙模型的含天然气水合物沉积物电阻率数值模拟［J］.天然气工业，2018，38（11）：128-134. CHEN Y F，WU N Y，LIANG D Q，et al.Numerical simulation of resistivity of natural gas hydrate deposits based on fractal pore model［J］.Natural Gas Industry，2018，38（11）：128-134.

27	KANG D J，LU J A，ZHANG Z J，et al.Fine-grained gas hydrate reservoir properties estimated from well logs and lab measurements at the Shenhu gas hydrate production test site，the northern slope of the South China Sea［J］.Marine and Petroleum Geology，2020，122：104676.

28	苏明，解习农，王振峰，等.南海北部琼东南盆地中央峡谷体系沉积演化［J］.石油学报，2013，34（3）：467-478. SU M，XIE X N，WANG Z F，et al.Sedimentary evolution of the central canyon system in Qiongdongnan Basin，northern South China Sea［J］.Acta Petrolei Sinica，2013，34（3）：467-478.

29	谢玉洪，童传新，范彩伟，等.琼东南盆地断裂系统特征与演化［J］.大地构造与成矿学，2015，39（5）：795-807. XIE Y H， TONG C X， FAN C W， et al. Characteristics and evolution of fault system in Qiongdongnan Basin［J］.Geotectonica et Metallogenia，2015，39（5）：795-807.

30	岳翀，赵晓明，葛家旺，等.琼东南盆地莺歌海组陆架边缘轨迹演化及主控因素［J］.沉积学报，2023，41（1）：110-125. YUE C， ZHAO X M， GE J W， et al. Evolution and main controlling factors of shelf margin trajectory in Yingge Formation， Qiongdongnan Basin［J］.Acta Sedimentologica Sinica，2023，41（1）：110-125.

ZHANG W， LIANG J Q， SU P B， et al.Distribution and characteristics of mud diapirs， gas chimneys， and bottom simulating reflectors associated with hydrocarbon migration and gas hydrate accumulation in the Qiongdongnan Basin，northern slope of the South China Sea［J］.Geological Journal，2019，54（6）：3556-3573.

32	莫修文，陆敬安，沙志彬，等.确定天然气水合物饱和度的测井解释新方法［J］.吉林大学学报（地球科学版），2012，42（4）：921-927. MO X W， LU J A， SHA Z B， et al. A new logging interpretation method for determining gas hydrate saturation［J］. Journal of Jilin University（Earth Science Edition），2012，42（4）：921-927.

Options

Outlines

模态框（Modal）标题

Abstract

Cite this article

0 引言

1 岩电实验

1.1 岩样制备及过程

表1 岩电实验岩样配比

1.2 实验过程及饱和度确定

图1 岩电实验装置概况

图2 反应釜内水合物生成过程

表2 不同粒径大小水合物岩样岩电实验数据

表3 不同泥质含量水合物岩样岩电实验数据

1.3 实验数据分析

图3 不同粒径水合物沉积物的电阻率和电阻率增大系数与水合物饱和度的关系

图4 不同泥质含量水合物沉积物的电阻率和电阻率增大系数(a)与水合物饱和度关系(b)

2 饱和度模型的建立

2.1 实验分析岩电规律

图5 水合物岩样地层因素—孔隙度关系与电阻率增大系数—含水饱和度关系

2.2 岩电规律的数值模拟

图6 三维数字岩心模型（骨架和水合物两相）

图7 水合物岩样在不同水合物饱和度条件下对应的三维模型

表4 数字岩心各组分电性参数

图8 水合物数字岩心在3个方向上的电阻增大系数与含水饱和度的关系

2.3 饱和度模型的建立

3 应用及效果分析

图9 X井饱和度解释成果

图10 Y井饱和度解释成果

表5 不同模型饱和度计算误差对比

4 结论

References

1.1　岩样制备及过程

1.2　实验过程及饱和度确定

1.3　实验数据分析

2.1　实验分析岩电规律

2.2　岩电规律的数值模拟

2.3　饱和度模型的建立