Natural Gas Geoscience >

2024 , Vol. 35 >Issue 4: 573 - 584

DOI: https://doi.org/10.11764/j.issn.1672-1926.2023.09.014

EUR evaluation method for producing shale gas wells in early stages： Case study of CN Gas Field in the Sichuan Basin

  • Fang LI , 1 ,
  • Lihong WU 2 ,
  • Haiyong YI 2 ,
  • Xu XU 3 ,
  • Xin JIANG 4 ,
  • Juan WU 1
Expand
  • 1. Exploration and Development Research Institute of PetroChina Southwest Oil & Gasfield Company，Chengdu 610041，China
  • 2. PetroChina Southwest Oil & Gasfield Company，Chengdu 610051，China
  • 3. Chongqing Gas Mine of PetroChina Southwest Oil & Gasfield Company，Chongqing 401120，China
  • 4. Shale Gas Research Institute of PetroChina Southwest Oil & Gasfield Company，Chengdu 610056，China

Received date: 2023-06-06

  Revised date: 2023-09-15

  Online published: 2023-10-19

Supported by

The Forward-looking Fundamental Technical Research Project of the Science and Technology Management Department of China National Petroleum Corporation(2022DJ7902)

the Technology Project of Southwest Oil and Gasfield Company, PetroChina(20190301-20)

Fold

Abstract

With the large-scale development of shale gas at home and abroad， more and more shale gas reserve assets are entering the international capital market， the calculation of gas well EUR has become a hot spot. However， it is difficult to judge the effect of reservoir fracturing only based on the limited production data at the initial stage of gas well production， resulting in large calculation error of gas well EUR and unable to judge the investment benefit of exploration and development. To this end， a “corrected gas well production percentile typical curve prediction method” is established，which uses the flow morphology method to screen gas wells in the middle and late stages of production in the well area as sample wells. Based on the historical production and EUR distribution of the sample wells， a corrected production percentile typical curve is established， and this curve is used to accurately calculate the EUR of gas wells in the early stages of production in the well area. The research results indicate that： （1） Using flow morphology diagnosis method to quantitatively determine the production stage can significantly improve the accuracy of EUR calculation for gas wells in the middle and later stages of production； （2） the corrected production percentile typical curve can represent the production development trend of gas wells in the well area， and can significantly improve the accuracy of EUR calculation for gas wells in the early stages of production. Therefore， the key technology for calculating the EUR of shale gas production in the early stage is “analogy”， which can quantitatively determine the production stage of gas wells in the well area. Through the “EUR percentile map” and the “typical production percentile curve”， the production laws of gas wells in the middle and later stages of production can be reasonably analogized and applied to the calculation of the EUR of gas wells in the early stage of production. The method has high reliability. The innovation of this study lies in the first proposal of a EUR calculation method based on the EUR percentile map and typical production percentile curves for gas wells during the early production stage， filling the technical gap in this field.

Key words： Shale gas; EUR; Percentile plate; Production percentile typical curve; Two-segement hyperbolic decline model

Cite this article

Fang LI , Lihong WU , Haiyong YI , Xu XU , Xin JIANG , Juan WU . EUR evaluation method for producing shale gas wells in early stages： Case study of CN Gas Field in the Sichuan Basin[J]. Natural Gas Geoscience, 2024 , 35(4) : 573 -584 . DOI: 10.11764/j.issn.1672-1926.2023.09.014

0 引言

最终可采量（Estimated Ultimate Recovery，简称EUR），是指自投产开始，到某一指定日期、某一废弃压力界限或某一单井最低极限日产油（气）量为截止值计算的可采出油（气）量［1］。EUR的定义源于“石油资源管理体系”（Petroleum Resource Management System，PRMS），其明确指出：“为清晰起见，EUR必须参照资源的相关技术和商业条件”［2］。例如，在美国证券交易委员会（SEC）的准则中，EUR的内涵为经济可采的。因此，为区分EUR本身技术与经济可采的内涵，下文中“EUR”默认为“经济的最终可采量”，而“技术的最终可采量”（Technical Estimated Ultimate Recovery）简称为“TEUR”。近年来，随着国内外页岩气的规模开发，越来越多的页岩气储量资产走向国际资本市场，页岩气EUR的准确计算能够极大降低勘探开发投资风险，提高企业竞争力，是目前研究的热点问题。
页岩气EUR计算方法分为容积法和动态法，由于行业内普遍认为页岩气藏可视为“人造气藏”，以静态参数为基础的容积法难以和实际EUR相匹配，因此，页岩气EUR的计算一般采用动态法，其主要包括：数值模型模拟法、解析模型模拟法、产量递减法、现代产量递减法和概率法。但是，国内外页岩气EUR计算方法以勘探开发成熟区为样本进行推导建立，侧重生产中后期的计算与评价，不完全适应投产初期的单井EUR计算。四川盆地页岩气藏一般采用压裂水平井开发，在不控压的生产条件下，产量短时间达到峰值后，快速递减，一段时间后又开始缓慢递减，投产初期气井生产数据匮乏，难以准确描述其水力裂缝长度、裂缝导流能力、体积压裂改造区平均孔隙度及渗透率等关键参数，加上页岩气储层中的多尺度渗流理论尚不完善，因此，在页岩气井投产初期，运用上述方法预测未来产量，得到的EUR可靠度低，难以准确判断EUR的技术可靠性或经济性［3-19］。
四川盆地页岩气开发在五峰组—龙马溪组海相页岩首先取得突破，正在探索其他层系，从2016年起步入规模建产阶段，但与北美地区相比，起步晚，处于勘探开发初期，四川盆地页岩气EUR计算评价体系主要从北美引进，对于投产初期气井评估不确定性大：借鉴北美页岩气田典型不控压生产气井生产规律（图1），四川盆地采用分段双曲递减模型对递减阶段产量进行预测以计算单井EUR，模型如下［20］：
q(t)= C q i 1 [ 1 + ( t - t 0 ) b 1 D i 1 ] - 1 b 1 , t < t * C q i 2 [ 1 + ( t - t 0 ) b 2 D i 2 ] - 1 b 2 , t > t * q i 2 = C q i 1 [ 1 + ( t * - t 0 ) b 1 D i 1 ] - 1 b 1
式中：q为气井产量，104 m3/d；q i1为产量递减第一阶段初始产量，104 m3/d；q i2为产量递减第二阶段初始产量，104 m3/d；D i1为产量递减第一阶段的初始年递减率，%/a；D i2为产量递减第二阶段的初始年递减率，%/a；b 1为产量递减第一阶段的递减指数，小数；b 2为产量递减第二阶段的递减指数，小数；t为绝对生产时间，d；t 0为递减开始前的绝对生产时间，d；t *为递减阶段分段时间，d；C为产量与递减率转换为一致时间单位时采用的常数。
图1 北美五大页岩气藏典型井产量趋势曲线

Fig.1 Typical well production trend curve of the five major shale gas reservoirs in North America

该方法相比其他“一段式”产量预测模型，适应性相对强，但是分段的时间是模型关键参数，特别是生产时间短的井，若仅依据邻近区块类比或根据经验确定分段时间，在开发初期，不确定性大，难以准确评价勘探开发投资的风险，如四川盆地CN气田部分气井EUR计算结果经历投产初期的波动后趋于稳定（图2）。其原因在于页岩气作为非常规油气，用邻井推测未钻井区域的生产动态特征具有不可靠性［21］，根据四川盆地的开发实践，即使在井网密度较低的钻井区域，页岩气井“邻区可类比”的特性差，同一平台不同分支气井动态特征可能存在较大差异。
图2 CN气田2016年投产气井单井EUR历年计算结果对比

Fig.2 Comparison of EUR calculation results for single wells in CN Gas Field in 2016

1 方法原理

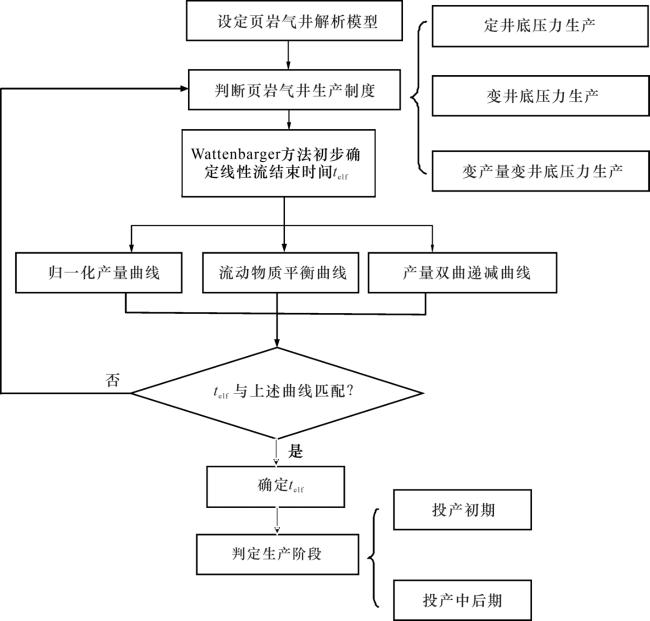
1.1　方法概述

针对投产初期气井EUR计算结果可靠度低的问题，运用流动形态法筛选井区内处于生产中后期气井作为样本井，根据样本井历史产量与EUR分布建立3条校正的产量百分位典型曲线：产量百分位90曲线、百分位50曲线、百分位10曲线，以这些曲线实现井区内投产初期气井EUR的准确计算。方法技术路线为：
首先划定样本井选取范围，对样本井进行流动形态诊断，接着筛选样本井，绘制TEUR百分位图版，并确保样本井百分位10/百分位90<5，之后绘制样本井产量百分位90、百分位50、百分位10典型曲线，在此基础上，用TEUR的百分位90、百分位50、百分位10值校正相应产量百分位典型曲线递减参数，然后根据目标井峰值产量选择相应产量百分位典型曲线模型预测目标井产量剖面，最后根据经济极限产量截断产量剖面得到EUR（经济EUR）。
因此，页岩气井投产初期单井EUR计算方法包括3项关键技术：投产初期气井准确识别、TEUR百分位图版与产量百分位典型曲线的建立、产量百分位典型曲线的校正。

1.2　投产初期气井准确识别

在以往的研究中，依据部分代表井生产规律发生显著变化的生产时间平均值，划定统一的产量分段时间点，然后采用分段的模型对页岩气产量进行拟合预测，但是各井产量实际分段时间往往区别明显，导致EUR计算结果可靠度低。为避免这一情况，首次提出运用流动形态诊断方法计算单井分段时间点的方法，准确判断其所处的生产阶段，识别筛选投产初期与中后期气井，提高分段双曲递减模型预测EUR的精度。
压裂后的页岩气水平井至少存在以下４个流动阶段：早期线性流动阶段、双线性流阶段、晩期线性流动线性阶段和边界反映阶段。阶段1—阶段3即为页岩气井投产初期，该阶段产量快速上升达到峰值后快速递减，流动形态为线性流；阶段4开始之后为生产中后期，该阶段产量缓慢递减，产量变化规律符合双曲递减模型，流动形态为边界流，产量分段时间点即是线性流结束时间点，其确定方法如下：
建立页岩气井裂缝渗流模型，渗流通道主要为水力裂缝，水力裂缝形态为“双翼缝”，假设裂缝完全贯穿储层，长度相等，裂缝以水平段为对称轴，如图3所示。基质为气体储集空间，基质与基质之间，基质与裂缝之间均存在流动，不考虑气体在基质中的解吸附效应，不考虑水相。
图3 页岩气井裂缝渗流模型示意

Fig.3 Schematic diagram of shale gas well fracture seepage model

在定井底流压生产制度下，改造区线性流结束时间t elf为：
t e l f = C c 1 A h ϕ μ g c t m c ψ p i - ψ p w f 200.6 T 2
式（2）中：t elf为改造区线性流结束时间，d；A为页岩气井压裂改造区等效面积（SRV面积），m2，由试井、微地震解释等初步确定；h为压裂改造储层厚度，m；T为气藏绝对温度，K； ψ p i为气藏原始拟压力，MPa2/（mPa·s）； ψ p w f为井底流动拟压力，MPa2/（mPa·s）； ϕ为改造区平均孔隙度，小数； μ g为天然气黏度，mPa·s。 c t为当前地层压力下气体压缩系数，1/MPa；C c1为国际单位制向油田单位制的转换系数，常数。mc为产量的倒数 1 / q与平方根绝对生产时间t 0.5曲线的斜率，d1.5/104 m3；在变井底压力生产制度下，改造区线性流结束时间t elf为：
t e l f = C c 2 A h ϕ μ g c t m v ψ p i - ψ p w f 200.6 T 2
式（3）中：m v为归一化拟压力 ψ p i - ψ p w f / q与平方根绝对生产时间t 0.5曲线的斜率，［MPa2/（mPa·s）］/104 m3/d1.5；C c2国际单位制向油田单位制的转换系数，常数。
而在变井底压力变产量生产制度下，改造区线性流结束时间t elf为：
t e l f = C c 2 A h ϕ μ g c t m s ψ p i - ψ p w f 200.6 T 2
式（4）中：m s为归一化拟压力 ψ p i - ψ p w f / q与平方根物质平衡时间t c 0 .5曲线的斜率，［MPa2/（mPa·s）］/104m3/d1.5；物质平衡时间t c表达式为：
t c = Q n q n
式（5）中：t c为物质平衡时间，d； qn 为变产量生产制度下，第n个微小时段的平均产量，m3/d；Qn 为变产量生产制度下，n个微小时段的累积产量，m3。
在线性流动阶段结束后进入边界流阶段，边界流阶段的产量发展规律可用双曲递减模型描述，产量表达式为：
q = q e l f 1 + b D e l f t - t e l f 1 / b
式（6）中：b为递减指数，小数；D elf为线性流阶段结束后天然气产量初始递减率，小数； q elf为边界流动结束时的产量，104 m3/d。
在选用式（2）—式（4）求得改造区线性流结束时间t elf后，需根据t elf计算此时改造区域的地质储量，并绘制A—G流动物质平衡曲线，根据所计算的改造区原始天然气地质储量（OGIP）对流动物质平衡曲线进行拟合，根据拟合效果逐步调整t elf值，直至达到最佳拟合效果，以最终确定t elf值。考虑页岩气的解吸附，根据t elf值计算改造区地质储量的公式如下：
G = f c p 200.8 T t e l f ϕ μ c t i m ϕ i S g i B g i + V L p i p i + p L
式（7）中：
c t = S c g + c d
式（8）中： c g为游离气压缩系数，1/MPa； c d为吸附气压缩系数，1/MPa； f c p为压降影响造成斜率误差的修正因子，其表达式为：
f c p = 1 - 0.085   2 D D - 0.085   7 D D 2
式（9）中： D D为无因次压力降，表达式为：
D D = ψ p i - ψ p w f ψ p i
非稳态流区域直线斜率m是一个与地层参数有关的参数。计算公式如下：
m = 3.154 T h ϕ μ g c t i 1 ψ p i - ψ p w f x f K
式（10）—式（11）中：K为改造区平均渗透率，10-3 μm2；x f为水力压裂缝半长，m；m为非稳态流区域直线斜率，［MPa2/（mPa·s）］/m3/d1.5。
将计算的t elf与气井实际生产时间对比即可确定气井生产阶段，生产时间大于t elf的气井处于生产中后期，此时令：
t*=t elf
将（12）式代入式（1）得：
q(t)= C q i 1 [ 1 + ( t - t 0 ) b 1 D i 1 ] - 1 b 1 , t < t e l f C q i 2 [ 1 + ( t - t 0 ) b 2 D i 2 ] - 1 b 2 , t > t e l f q i 2 = C q i 1 [ 1 + ( t e l f - t 0 ) b 1 D i 1 ] - 1 b 1
在获得可靠的递减分段时间后t elf后，递减第二阶段的递减指数b 2的可靠度也会相应提高，b2 由下式计算：
b 2 = d d t 1 D i 2 = - d d t q d q / d t
上述t elf确定的流程如图4所示。
图4 页岩气井生产阶段判定技术路线

Fig.4 Technical roadmap for determining the production stage of shale gas wells

式（13）可准确预测未来产量，并利用经济极限产量对其进行截断，得到单井EUR，以CN区块部分2016年投产气井为例，运用流动形态诊断，确定分段时间点，能够显著提高分段双曲递减模型计算EUR的精度，如表1所示。
表1 生产阶段定量划分前后评估精度对比明细

Table 1 Comparison of evaluation precision before and after quantitative division of production stage

序号 井号 投产时间

EUR1

/（108 m3）

 经验取值分段时间/d 流动形态诊断分段时间/d 经验取值b 2（小数） 流动形态诊断b 2（小数）

EUR2

/（108 m3）

EUR3

/108 m3）

 不诊断计算EUR误差/% 诊断计算EUR误差/%
平均值 319 12.57 2.16
1 CN-72 2016/01/20 1.37 365 212 0.70 0.50 1.01 1.00 37.00 1.00
2 CN-73 2016/01/07 1.12 365 126 0.70 0.70 1.28 1.25 10.40 2.40
3 CN-74 2016/01/08 1.12 365 285 0.70 0.50 1.07 1.10 1.82 2.73
4 CN-75 2016/01/08 1.44 365 148 0.70 0.60 1.62 1.59 9.43 1.89
5 CN-76 2016/01/20 1.39 365 171 0.70 0.50 1.31 1.33 4.51 1.50
6 CN-77 2016/04/30 1.26 365 348 0.70 0.60 1.18 1.22 3.28 3.28
7 CN-78 2016/05/02 1.29 365 175 0.70 0.65 1.18 1.22 5.74 3.28
8 CN-79 2016/05/07 0.8 365 573 0.70 0.50 0.97 1.02 21.57 4.90
9 CN-80 2016/06/13 0.9 365 156 0.70 0.70 1.03 1.02 11.76 0.98
10 CN-81 2016/06/13 1.24 365 574 0.70 0.58 1.07 1.09 13.76 1.83
11 CN-82 2016/06/13 1.17 365 223 0.70 0.50 1.04 1.07 9.35 2.80
12 CN-83 2016/09/29 1.39 365 146 0.70 0.70 1.20 1.26 10.32 4.76
13 CN-84 2016/10/06 1.19 365 76 0.70 0.60 1.08 1.11 7.21 2.70
14 CN-85 2016/10/07 1.16 365 179 0.70 0.70 1.24 1.24 6.45 0.00
15 CN-86 2016/10/13 0.96 365 296 0.70 0.80 1.19 1.20 20.00 0.83
16 CN-87 2016/11/26 1.04 365 632 0.70 0.90 1.21 1.22 14.75 0.82
17 CN-88 2016/11/27 1.09 365 651 0.70 0.70 1.25 1.23 11.38 1.63
18 CN-89 2016/11/27 0.95 365 776 0.70 0.60 1.33 1.31 27.48 1.53

注：EUR1为采用2017年数据不诊断计算EUR； EUR2为采用2017年数据诊断计算EUR； EUR3为国际机构2020年披露EUR

由表1可见，以2020年国际评估机构披露结果为标准，仅凭经验确定产量分段点（表中实例统一取值365 d）计算EUR，18口气井EUR在2017年平均相对误差为12.57%，而定量划分生产阶段后，评估平均相对误差降低为2.16%。

1.3　页岩气井TEUR百分位图版与产量百分位典型曲线的建立

在同一井区内，通过流动形态诊断选取处于生产中后期的井作为样本井并运用式（13）计算所有样本井EUR，为排除气价、操作成本变化对样本井EUR的影响，此时采用技术极限产量对预测产量剖面进行截断，得到TEUR，其余处于投产初期井为目标井。以样本井TEUR以10为底的对数值为水平轴，累积百分比为纵轴，绘制累积百分比—对数TEUR曲线，若样本井TEUR的概率分布为正态分布，则累积百分比—对数TEUR曲线近似为直线，采用线性模型拟合该曲线后，得到线性模型计算的TEUR百分位90值、百分位50值、百分位10值。应当指出，图版中的累积百分比实际上并不表示概率的含义，而实际指所有本井TEUR数值的排位，例如，百分位10值指井组中排名前10%的TEUR值，故将该图版称为TEUR百分位图版。若TEUR百分位图版中曲线不呈直线或出现百分位10值/百分位90值大于5的情况，根据非常规气评估准则，说明初选样本井中包含了不同地质条件或完井工艺的井，需要剔除这些井，以满足上述2个条件［21］，其中本质的原因在于当百分位10值/百分位90值大于5时，TEUR的分布可能并不呈现正态分布，所有样本所控制的区域并不能作为一个非常规气区，即并不满足采用TEUR百分位图版相关方法的前提条件，因此，即使在满足TEUR百分位10值/百分位90值小于5的条件下，也应对样本井TEUR进行正态分布检验。
在绘制TEUR百分位图版后，将样本井的生产历史数据与绝对生产时间点对齐，然后计算产量百分位90典型曲线、百分位50典型曲线、百分位10典型曲线数据点。产量百分位典型曲线数据点计算方法如下：
将某一时间点的所有井产量数据升序排列，以N表示数据点的数目，P表示百分位，如百分位90对应的P为10，则P对应的站位数n以下式计算：
n = P 100 N - 1 + 1
接着，将站位数劈分为整数k和小数d，即为：
n = k + d
最后P对应的产量值qP 为：
q P = q k + d q k + 1 - q k
式（17）中： q k为升序排列的同时间点产量数据中排序为k的产量数据，104 m3/d； q k + 1为升序排列的同时间点产量数据中排序为k+1的产量数据，104 m3/d。
根据式（15）—式（17）逐一计算3条产量百分位典型曲线所有历史时间点产量数据后，即可绘制产量百分位典型曲线图。

1.4　基于TEUR百分位图版的产量百分位典型曲线的校正

在绘制TEUR百分位典型曲线后，运用式（1）所示的分段双曲模型对这3条曲线进行最小二乘算法拟合，得到相关的模型参数：q i1，b 1，q i2，D i1，b 2，D i2， t*。接着，利用TEUR百分位90、百分位50及百分位10值对相应的产量百分位典型曲线的第二阶段递减率D i2进行校正，确保校正后产量百分位典型曲线预测计算的TEUR，与对应的百分位TEUR值相等，这样就建立了基于TEUR百分图版与产量百分位典型曲线的分段产量预测模型。调整后的D i2记为 D i 2 '，其计算式如下：
D i 2 ' = C ' q i 2 b 2 - 1 G p 2 1 q t l b 2 - 1 - 1 q i 2 b 2 - 1
G p 2 = T E U R p - G p 1 - G p 0
式（18）—式（19）中： C '为单位时间产量与累积产量单位转换为一致的常数；q tl为技术极限产量，104 m3/d；G p0为产量递减开始之前的累积产量，104 m3；G p1为产量递减第一阶段的累积产量，104 m3；G p2为产量第二阶段的累积产量，104 m3；TEURp为百分位图版中与百分位典型曲线对应的百分位TEUR，108 m3。
在求得 D i 2 '后，即可得到目标井（投产初期井）EUR的计算模型如下：
E U R = G p 0 + G p 1 + G p 2
上式中：
G p 1 = C ' q i 1 b 2 - 1 D i 1 1 q i 2 b 1 - 1 - 1 q i 1 b 1 - 1
G p 2 = C ' q i 2 b 2 - 1 D i 2 ' 1 q e l b 2 - 1 - 1 q i 2 b 2 - 1
式（20）—式（22）中：q el为经济极限产量，104 m3/d。
需要说明的是，除了采用式（20），也可直接利用 D i 2 '和剩余的产量百分位典型曲线分段递减模型参数预测未来产量，在产量低于技术极限产量时截断，即预测TEUR产量剖面，然后利用经济极限产量截断TEUR产量剖面，得到EUR值。TEUR百分位图版法中的TEUR值应与产量百分位典型曲线预测的TEUR相等是该方法的理论基础，是同一井组的TEUR的不同表现形式，但是由于产量百分位典型曲线形态受气井产量波动的影响（工作制度调整、增产措施作业等引起产量波动），因此，需要借助TEUR百分位图版的对应值校正初始曲线的递减参数，使得预测的EUR可靠。

1.5　基于产量峰值的产量百分位典型曲线选用

运用1.4节中的方法建立产量百分位曲线及分段产量递减模型后，对于目标井EUR的预测计算，需要根据目标井峰值产量与产量百分位典型曲线峰值产量的接近程度选择相应曲线，因为气井EUR的直接表征量为峰值产量，在地质条件、完井工艺相近的条件下，峰值产量相近的井产量趋势也趋于一致。3条产量百分位典型曲线中百分位10典型曲线代表区块中峰值产量高，产量后期递较快，即储层改造效果好的井；百分位90曲线代表峰值产量低，产量后期递减缓慢，储层改造效果不佳的井，百分位50典型曲线代表储层改造效果居中的井。

2 实例分析

四川盆地CN气田A井区有投产井99口，这些井的地质条件与完井工艺相近，这些井均采用本地区2019年前的完井工艺，即“单段低簇数长簇间距+低加砂强度”的工艺，从水平井长度看，99口气井水平段长度分布在980~2 556 m之间，平均值为1 526 m，其中65%的气井水平段长度在1 500 m左右（图5）。通过流动形态诊断，筛选出71口生产进入中后期且EUR能够可靠计算的井，将其中前60口井作为样本井，后11口井作为目标井以验证方法的可靠性。这71口井产量分段时间及TEUR计算结果如表2所示，相应技术极限产量为1 000 m3/d，经济极限产量为5 000 m3/d。
图5 99口气井水平段长度对比

Fig.5 Comparison of horizontal length of 99 gas wells

表2 CN气田A井区生产中后期井产量分段时间及TEUR计算结果

Table 2 The well production staging time and TEUR calculation results of well area A in CN Gas Field in the middle and later stage of production

序号 井号 分段时间t */d

第二阶段产量

递减指数b 2

 技术最终可采量TEUR/（108 m3） 序号 井号 分段时间t */d

第二阶段产量

递减指数b 2

 技术最终可采量TEUR/（108 m3）
1 CN-1 182 0.55 1.21 37 CN-37 366 0.55 1.36
2 CN-2 183 0.60 0.87 38 CN-38 127 0.65 0.83
3 CN-3 123 0.70 0.88 39 CN-39 235 0.54 0.76
4 CN-4 270 0.55 0.80 40 CN-40 164 0.5 1.04
5 CN-5 155 0.55 1.82 41 CN-41 113 0.8 0.7
6 CN-6 613 0.65 0.96 42 CN-42 152 0.6 0.7
7 CN-7 330 0.60 1.22 43 CN-43 197 0.58 1.23
8 CN-8 358 0.60 0.40 44 CN-44 125 0.7 1.38
9 CN-9 39 0.60 0.48 45 CN-45 176 0.7 1.38
10 CN-10 145 0.45 1.14 46 CN-46 250 0.7 1.18
11 CN-11 464 0.70 0.38 47 CN-47 291 0.47 1.35
12 CN-12 164 0.80 1.01 48 CN-48 383 0.55 1.19
13 CN-13 338 0.80 0.89 49 CN-49 406 0.55 1.15
14 CN-14 357 0.70 1.43 50 CN-50 188 0.7 1.51
15 CN-15 367 0.60 0.98 51 CN-51 105 0.51 1.48
16 CN-16 355 0.24 1.16 52 CN-52 126 0.7 1.41
17 CN-17 548 0.70 0.54 53 CN-53 285 0.5 1.39
18 CN-18 344 0.70 0.73 54 CN-54 188 0.55 1.58
19 CN-19 210 0.52 1.22 55 CN-55 148 0.6 1.96
20 CN-20 404 0.70 1.39 56 CN-56 77 0.7 1.61
21 CN-21 463 0.70 1.07 57 CN-57 245 0.6 1.91
22 CN-22 156 0.70 1.18 58 CN-58 76 0.6 1.31
23 CN-23 574 0.58 1.21 59 CN-59 212 0.5 1.12
24 CN-24 675 0.00 1.14 60 CN-60 171 0.7 1.22
25 CN-25 348 0.60 1.37 61 CN-61 157 0.7 0.99
26 CN-26 175 0.65 1.37 62 CN-62 230 0.6 1.01
27 CN-27 573 0.50 1.15 63 CN-63 272 0.6 1.18
28 CN-28 229 0.50 1.29 64 CN-64 372 0.5 1.15
29 CN-29 155 0.50 1.13 65 CN-65 146 0.7 1.22
30 CN-30 329 0.50 1.07 66 CN-66 179 0.7 1.26
31 CN-31 183 0.65 0.90 67 CN-67 181 0.6 0.96
32 CN-32 209 0.60 1.06 68 CN-68 209 0.7 0.86
33 CN-33 295 0.50 1.26 69 CN-69 120 0.7 1.25
34 CN-34 179 0.43 1.47 70 CN-70 62 0.5 1.3
35 CN-35 668 0.60 0.63 71 CN-71 112 0.5 0.94
36 CN-36 140 0.75 1.74
选择CN-1井至CN-60井作为样本井，绘制这些井TEUR百分位图版，如图6所示，TEUR的百分位90值线性拟合结果为0.687×108 m3，百分位50值线性拟合结果为1.096×108 m3，百分位10值线性拟合结果为1.747×108 m3，百分位10与百分位90的比值为2.54，小于5，同时，TEUR呈正态分布（柯尔莫戈洛夫—斯米诺夫检验显著性为0.20，大于0.05），说明CN-1井至CN-60井可作为一组样本井。此外，所有71口井TEUR也呈正态分布（柯尔莫戈洛夫—斯米诺夫检验显著性为0.20，大于0.05）。
图6 CN气田A井区60口样本井TEUR累积概率曲线

Fig.6 Cumulative probability curve of TEUR for 60 sample wells in well block A of CN Gas Field

根据样本井的生产历史数据，运用式（15）—式（17），计算这些井的产量百分位90、百分位50、百分位10典型井数据，并运用分段双曲递减模型拟合这3条典型曲线的数据，得到产量百分位典型曲线分段双曲递减模型，典型曲线的拟合图如图7—图9所示：
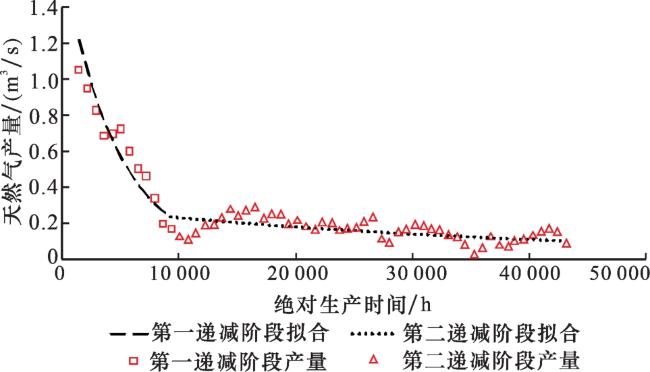
图7 CN气田A井区产量百分位90典型曲线及分段双曲递减模型拟合图

Fig.7 Typical 90 percentile production curve and fitting diagram of segmented hyperbolic decline model in well area A of CN Gas Field

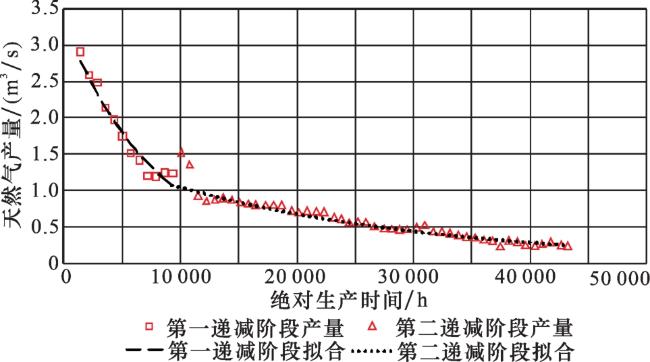
图8 CN气田A井区产量百分位50典型曲线及分段双曲递减模型拟合图

Fig.8 Typical 50 percentile production curve and fitting diagram of segmented hyperbolic decline model in well area A of CN Gas Field

图9 CN气田A井区产量百分位10典型曲线及分段双曲递减模型拟合图

Fig.9 Typical 10 percentile production curve and fitting diagram of segmented hyperbolic decline model in well area A of CN Gas Field

上述3条典型曲线对应的分段双曲递减模型拟合参数如表3所示。
表3 CN气田A井区典型曲线分段双曲递减模型参数

Table 3 Parameters of typical curve segmentation hyperbolic decline model in well area A of CN Gas Field

典型曲线 分段时间t elf/d

第一阶段递减初始产量q i1

/（m3/d）

 第一阶段递减初始递减率D i1/%

第一阶段递减指数b 1

（小数）

第二阶段递减初始产量q i2

/（m3/d）

 第二阶段递减初始递减率D i2 /（%）

第二阶段递减指数b 2

（小数）
百分位90 422.089 112 530 78.849 5 0.01 18 844.6 15.55 0.01
百分位50 414.592 213 236 76.262 1 0.01 41 633.8 21.53 0.01
百分位10 422.089 298 343 82.789 8 1.05 100 320.0 41.52 0.29
为确保产量百分位90、百分位50、百分位10典型曲线对应的分段双曲递减模型在技术极限产量1 000 m3/d时所预测计算的TEUR与TEUR百分位图版中的百分位90，百分位50，百分位10值一一对应，运用式（18）对3条典型曲线递减模型第二段初始递减率D i2进行校正，结果如表4所示。
表4 CN气田A井区典型曲线分段双曲递减第二阶段递减率调整对比

Table 4 Comparison of the adjustment of the second stage decline rate of the typical curve segmented hyperbolic decline in well area A of CN Gas Field

典型曲线 第二阶段递减初始递减率D i2/% 校正的第二阶段递减初始递减率D' i2/% 差异/%
百分位90 15.55 11.86 -23.73
百分位50 21.53 20.16 -6.36
百分位10 41.52 41.33 -0.46
运用校正后的3条产量百分位典型曲线对验证井TEUR进行预测计算，并与基于流动形态诊断的分段双曲递减模型预测TEUR进行对比，结果如表5所示。
表5 CN气田A井区典型曲线分段双曲递减模型TEUR计算结果对比

Table 5 Comparison of TEUR calculation results of typical curve segmentation hyperbolic decline model in well area A of CN Gas Field

验证井号

百分位90典型曲线预测TEUR

/（108 m3）

百分位50典型曲线预测TEUR

/（108 m3）

百分位10典型曲线预测TEUR

/（108 m3）

基于流动形态诊断预测TEUR

/（108 m3）

 百分位90典型曲线预测相对误差/% 百分位50典型曲线预测相对误差/% 百分位10典型曲线预测相对误差/%

最佳

百分位曲线

最低误差

/%
总量或平均误差 20.87 14.90 12.68 13.71 50.74 15.70 10.84 3.53
CN-61 1.82 1.34 1.23 1.19 52.94 12.61 3.36 10 3.36
CN-62 1.87 1.33 1.44 1.43 30.77 6.99 0.70 10 0.70
CN-63 2.22 1.70 1.40 1.44 54.17 18.06 2.78 10 2.78
CN-64 2.29 1.73 1.38 1.51 51.66 14.57 8.61 10 8.61
CN-65 2.27 1.62 1.46 1.47 54.42 10.20 0.68 10 0.68
CN-66 2.72 1.92 1.36 1.46 86.30 31.51 6.85 10 6.85
CN-67 2.03 1.43 1.15 1.09 86.24 31.19 5.50 10 5.50
CN-68 1.19 0.85 0.75 0.86 38.37 1.16 12.79 50 1.16
CN-69 1.95 1.34 1.20 1.25 56.00 7.20 4.00 10 4.00
CN-70 1.53 1.06 1.03 1.07 42.99 0.93 3.74 50 0.93
CN-71 0.98 0.58 0.28 0.94 4.26 38.30 70.21 90 4.26
由表3可见，目标井EUR评估最佳曲线为典型曲线峰值产量与其实际值最接近的那一条：以基于流动形态诊断的分段双曲递减模型计算结果为参照，最佳百分位曲线单井平均误差仅为3.53%。验证井峰值产量与产量百分位典型曲线峰值产量对比如表6所示。
表6 验证井峰值产量与产量百分位典型曲线峰值产量对比

Table 6 Comparison of peak production and production percentile typical curve peak production of verification wells

验证井号

百分位90典型曲线峰值产量

/（104 m3/d）

百分位50典型曲线峰值产量

/（104 m3/d）

百分位10典型曲线峰值产量

/（104 m3/d）

验证井峰值

产量

/（104 m3/d）

 百分位90典型曲线峰值产量差异/% 百分位50典型曲线峰值产量差异/% 百分位10典型曲线峰值产量差异/% 峰值产量最接近的产量百分位曲线
CN-61 11.25 21.32 29.83 26.58 -57.67 -19.79 12.23 10
CN-62 11.25 21.32 28.83 31.58 -64.38 -32.49 -8.71 10
CN-63 11.25 21.32 28.83 29.60 -61.99 -27.97 -2.60 10
CN-64 11.25 21.32 28.83 30.20 -62.75 -29.40 -4.54 10
CN-65 11.25 21.32 28.83 41.28 -72.75 -48.35 -30.16 10
CN-66 11.25 21.32 28.83 38.59 -70.85 -44.75 -25.29 10
CN-67 11.25 21.32 28.83 36.36 -69.06 -41.36 -20.71 10
CN-68 11.25 21.32 28.83 21.23 -47.01 0.42 35.80 50
CN-69 11.25 21.32 28.83 30.53 -63.15 -30.17 -5.57 10
CN-70 11.25 21.32 28.83 20.92 -46.22 1.91 37.81 50
CN-71 11.25 21.32 29.83 10.21 10.19 108.81 192.16 90
在预测TEUR产量剖面后，利用式（20）—式（22）计算或直接利用经济极限产量5 000 m3/d，截断上述11口井的产量预测剖面，得到相应的EUR并与普通的分段双曲点模型法EUR计算结果对比，结果如表7所示。
表7 利用投产初期生产数据计算验证井EUR结果对比

Table 7 Comparison of EUR results of verification wells using production data from the initial production stage

序号 验证井号

基于流动形态诊断预测EUR

/（108 m3）

投产初期普通分段双曲递减模型计算EUR

/（108 m3）

投产初期产量百分位典型曲线EUR预测

/（108 m3）

 普通分段双曲递减模型法计算EUR相对误差/%

产量百分位典型曲线计算EUR相对

误差/%
总量或平均误差 13.04 12.43 12.79 26.68 3.85
1 CN-61 1.13 1.08 1.20 4.42 6.19
2 CN-62 1.36 1.03 1.37 24.26 0.74
3 CN-63 1.37 1.04 1.34 24.09 2.19
4 CN-64 1.43 1.01 1.31 29.37 8.39
5 CN-65 1.40 1.12 1.39 20.00 0.71
6 CN-66 1.39 1.18 1.29 15.11 7.19
7 CN-67 1.04 1.11 1.09 6.73 4.81
8 CN-68 1.19 0.87 1.14 26.89 4.2
9 CN-69 0.82 1.48 0.79 80.49 3.66
10 CN-70 1.02 1.74 1.00 70.59 1.96
11 CN-71 0.89 0.77 0.87 13.48 2.25
表7中普通分段递减模型法，根据经验统一取分段时间t* 为365 d，第二段递减指数b 2取0.7，第二段递减率D i2取邻近的生产井的后期递减率，以生产中后期，基于流动形态诊断且得到国际机构认可披露的EUR为基准，计算得到的单井EUR平均相对误差为26.68%，而百分位典型曲线仅为3.85%，表明EUR百分位图版与产量百分位典型曲线相结合的投产初期EUR计算方法显著提高了EUR计算可靠度。同时，百分位典型曲线的建立需要一定数量处于生产中后期的井，并确保所研究井区EUR百分位10/百分位90<5，因此，上述方法适用于开发成熟区。

3 结论

（1）不控压生产页岩气井投产初期EUR计算结果可靠度低的原因在于产量发展呈现“分段”特征，采用初期生产历史预测EUR不确定性大，基于线性流理论的流动形态诊断方法实现了“分段点”的锚定，进而可靠识别气井所处生产阶段，显著提高EUR计算可靠度，为后续EUR百分位图的建立奠定基础。
（2）TEUR百分位图反映了井组TEUR的排位特征，产量百分位典型曲线表征井组生产规律的排位特征，本文研究所建立的校正产量百分位典型曲线首次挖掘了二者的内在关联（产量是EUR的直接表现形式），巧妙地排除了产量波动对产量趋势的干扰，并通过气井峰值产量的对比，将所建立的产量百分位典型曲线合理类比应用于目标井EUR计算，建立了可靠的页岩气井投产初期EUR计算方法，填补了国内该领域的技术空白。

References

Publishing order | Descend order by publishing year | Descend order by cited within
1
张蕾，彭丹丹，金亚杰，等.SEC油气储量新准则［G］.北京：勘探与生产分公司储量管理处，2009：24-26.

ZHANG L，PENG D D，JIN Y J，et al.New Criteria for Oil and Gas SEC Reserves［G］.Beijing：Reserve Management Division of Exploration and Production Company，2009：24-26.

2
SPE/WPC/AAPG/SPEE.Petroleum Resources Management System［DB］. Texas： SPE Oil and Gas Reserves Committee，2007

3
潘林华，程礼军，陆朝晖，等.页岩储层水力压裂裂缝扩展模拟进展［J］. 特种油气藏，2014，21（4）：1-3.

PAN L H，CHENG L J，LU C H，et al.Simulation of hydraulic fracture propagation in shale reservoir［J］. Special Oil & Gas Reservoirs，2014，21（4）：1-3.

4
郭晶晶.基于多重运移机制的页岩气渗流机理及试井分析理论研究［D］. 成都：西南石油大学，2013：41-65.

GUO J J.Research on Multiple Migration Mechanisms and Well Testing Theory for Shale Gas Reservoirs［D］. Chengdu： Southwest Petroleum University，2013： 41-65.

5
郑海军.多段压裂水平井压力计算及分析方法［D］.北京：中国科学技术大学，2015：8-21.

ZHENG H J.Pressure Calculation and Analysis of Multi-fractured Horizontal Well［D］. Beijing： University of Science and Technology of China，2015：8-21.

6
邓世冠，鲁力，刘海娇，等.一种孔隙裂隙网络模型及页岩气渗流模拟［J］. 地下空间与工程学报，2015，11（增刊1）：76-79.

DENG S G，LU L，LIU H J， et al.Pore-fractural network model for compacted geomaterials and simulation of shale gas seepage［J］.Chinese Journal of Underground Space and Engineering，2015，11（supplement1）：76-79.

7
程远方，董丙响，时贤，等.页岩气藏三孔双渗模型的渗流机理［J］. 天然气工业，2012，32（9）：44-47.

CHENG Y F，DONG B X，SHI X， et al.Seepage mechanism of a triple-porosity dual-permeability model for shale gas reservoirs［J］.Natural Gas Industry，2012，32（9）：44-47.

8
赵金洲，符东宇，李勇明，等.基于改进三线性流模型的多级压裂页岩气井产能影响因素分析［J］. 天然气地球科学，2016，27（7）：1324-1330.

ZHAO J Z，FU D Y，LI Y M， et al.Analysis of sensitive factors about multistage fractured well productivity in shale gas reservoirs based on modified trilinear flow model［J］. Natural Gas Geoscience，2016，27（7）：1324-1330.

9
谢亚雄，刘启国，王卫红，等.页岩气藏多段压裂水平井产能预测模型［J］. 大庆石油地质与开发，2016，35（5）：163-168.

XIE Y X，LIU Q G，WANG W H， et al.Productivity predicting model of the multiple-stage fractured horizontal well in shale gas reservoirs［J］.Petroleum Geology & Oilfield Development in Daqing，2016，35（5）：163-168.

10
王伟，樊冬艳，孙海.页岩气藏分段多簇压裂水平井产能模型及影响因素分析［J］. 科学技术与工程，2015，15（31）：36-40.

WANG W，FAN D Y，SUN H.Productivity model and analysis of influence factors of staged multi-cluster fractured horizontal wells in shale gas reservoirs［J］.Science Technology and Engineering，2015，15（31）：36-40.

11
朱光普，姚军，樊冬艳，等.页岩气藏压裂水平井试井分析［J］.力学学报，2015，47（6）：945-952.

ZHU G P，YAO J，FAN D Y， et al.Pressure transient analysis of fractured horizontal well in shale gas reservoir［J］.Chinese Journal of Theoretical and Applied Mechanics，2015，47（6）：945-952.

12
周祥.页岩储层体积压裂产能数值模拟研究［D］. 北京：中国石油大学（北京），2016：22-34.

ZHOU X.Investigation into the Production Numerical Simulation on Shale Gas Reservoir with Volume Fracturing［D］. Beijing： China University of Petroleum（Beijing），2016：22-34.

13
李陈.页岩气非定常渗流理论及其试井应用［D］.北京：中国地质大学（北京），2013：32-38.

LI C.Transient Flow Theory of Shale Gas and Application on Well Test［D］. Beijing：China University of Geosciences（Beijing），2013：32-38.

14
姚同玉，黄延章，李继山.页岩中页岩气渗流系数计算模型［J］.应用数学和力学，2014，35（8）：939-946.

YAO T Y，HUANG Y Z，LI J S.Calculation model for the permeability coefficient of shale gas in shale matrix［J］.Applied Mathematics and Mechanics，2014，35（8）：939-946.

15
韩国庆，任宗孝，牛瑞，等.页岩气分段压裂水平井非稳态渗流模型［J］.大庆石油地质与开发，2017，36（4）：160-167.

HAN G Q，REN Z X，NIU R， et al.Unsteady seepage model of the shale-gas staged fractured horizontal well［J］. Petroleum Geology and Oilfield Development in Daqing，2017，36（4）：160-167.

16
郝进，姜振学，邢金艳，等.一种改进的页岩气损失气含量估算方法［J］. 现代地质，2015，29（6）：1475-1481.

HAO J，JIANG Z X，XING J Y，et al.An improved method of calculating lost gas content of shale gas［J］. Geoscience，2015，29（6）：1475-1481.

17
陈作，薛承瑾，蒋廷学，等.页岩气井体积压裂技术在我国的应用建议［J］. 天然气工业，2010，30（10）：30-32.

CHEN Z，XUE C J，JIANG T X， et al.Proposals for the application of fracturing by stimulated reservoir volume（SRV） in shale gas wells in China［J］.Natural Gas Industry，2010，30（10）：30-32.

18
赵天逸，宁正福，何斌，等.页岩等温吸附理论模型对比分析［J］. 重庆科技学院学报（自然科学版），2014，16（6）：55-58.

ZHAO T Y，NING Z F，HE B，et al.Comparative analysis of theoretical models of shale［J］.Journal of Chongqing University of Science and Technology（Science Edition），2014，16（6）：55-58.

19
MORIDIS G J，BLASINGAME T A，FREEMAN C M.Analysis of mechanisms of flow in fractured tight-gas and shale-gas reservoirs［C］// SPE Latin American and Caribbean Petroleum Engineering Conference，Lima，Peru：Society of Petroleum Engineers，2010.

20
刘会会，崔越华，吴优，等. 基于分段拟合的致密气藏递减分析方法［J］. 石油化工应用，2020，39（3）：20-24.

LIU H H，CUI Y H，WU Y，et al.Comparative decline analysis method for tight gas reservoirs based on piecewise fitting［J］.Petrochemical Industry Application，2020，39（3）：20-24.

21
王永祥，李建忠.非常规油气区带未开发储量评估指南［M］.北京：石油工业出版社，2012： 28-29.

WANG Y X，LI J Z.Udelines for the Practical Evaluation of Undeveloped Reserves in Resource Plays［M］.Beijing：Ptroleum Industry Press，2012：28-29.

Options
Outlines

/

〈 〉

陇ICP备2021001824号-7　 甘公网安备 62010202000678号
Copyright © Natural Gas Geoscience, All Rights Reserved.
Tel: (0931)8277790　
E-mail：geogas@lzb.ac.cn
Total visitors:　 Visitors of today: 　 Now online:
Powered by Beijing Magtech Co. Ltd,.