Natural Gas Geoscience >

2021 , Vol. 32 >Issue 11: 1601 - 1609

DOI: https://doi.org/10.11764/j.issn.1672-1926.2021.08.003

Temperature distribution prediction of horizontal wells during fracturing treatment

  • Haitao LI , 1 ,
  • Qing ZHANG 2 ,
  • Hao YU , 1 ,
  • Ye XIN 3 ,
  • Hongwen LUO 1 ,
  • Yuxing XIANG 1 ,
  • Ying LI 1 ,
  • Kairui YE 2
Expand
  • 1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China
  • 2. Shale Gas Exploration and Development Project Manager Department of CNPC Chuanqing Drilling Co. , Ltd. , Chengdu 610500, China
  • 3. Engineering Technology Branch, CNOOC Energy Development Co. , Ltd. , Tianjin 300450，China

Received date: 2021-04-25

  Revised date: 2021-08-10

  Online published: 2021-11-30

Supported by

The China National Science and Technology Major Project(2016ZX05021-005-009HZ)

the National Natural Science Foundation of China(41902161)

Fold

Highlights

In recent years, optical fiber distributed temperature sensor system (DTS) has been increasingly used in horizontal well fracturing dynamic monitoring, aiming to solve the technical problems commonly faced in the process of horizontal well fracturing, such as artificial fracture initiation location unknown, fracturing fluid whereabouts unknown, fracture propagation morphology unclear, fracturing effect difficult to evaluate. The temperature prediction model is the basis of fracturing diagnosis based on DTS monitoring, but it is still a great challenge to predict quantitatively the temperature distribution in the fracturing process of horizontal wells. Considering the basis of a variety of trace heating effect, this paper established a set of horizontal well staged fracturing temperature distribution prediction model and completes the solution coupling model. The established temperature model was used to simulate the temperature distribution of conventional fracturing and multistage fracturing in a horizontal well, and the temperature distribution characteristics in the process of multistage fracturing were analyzed. The effects of fracturing fluid displacement, formation filtration coefficient, fracture width and fracture height on temperature distribution were determined. The research results provide theoretical support for the realization of DTS based monitoring and diagnosis of fracturing performance, identification of fracture initiation and analysis of fracturing fluid direction, which is of great significance for the evaluation of fracturing effect and fracturing design optimization of fractured horizontal wells.

Cite this article

Haitao LI , Qing ZHANG , Hao YU , Ye XIN , Hongwen LUO , Yuxing XIANG , Ying LI , Kairui YE . Temperature distribution prediction of horizontal wells during fracturing treatment[J]. Natural Gas Geoscience, 2021 , 32(11) : 1601 -1609 . DOI: 10.11764/j.issn.1672-1926.2021.08.003

0 引言

近年来随着光纤测量技术的快速发展，分布式光纤温度测试技术（DTS）逐渐成熟，它可以探测微小的温度变化，实时提供准确而连续的温度数据［1］。基于分布式温度测试（Distributed Temperature Sensors，DTS）、生产测井工具（Production Logging Tool，PLT）等的井下温度测试越来越多地被用于水平井井下状况监测［2］，根据测得的井下温度数据，可以定性判断产水位置、识别流体类型、监测套管漏失，并用以诊断人工裂缝、评价压裂改造效果、评价完井效果等。通过建立理论模型，井下温度测试数据还可用于定量解释储层参数、裂缝参数、产出剖面预测等。罗红文等［3-7］建立了考虑微热效应的低渗气藏两相渗流时压裂水平井的耦合预测模型，并且建立了一套模拟低渗气藏压裂水平井生产过程温度剖面的理论模型，通过井筒温度剖面对压裂过程中的各项参数进行敏感性评价，并对生产过程中的温度分布进行了预测。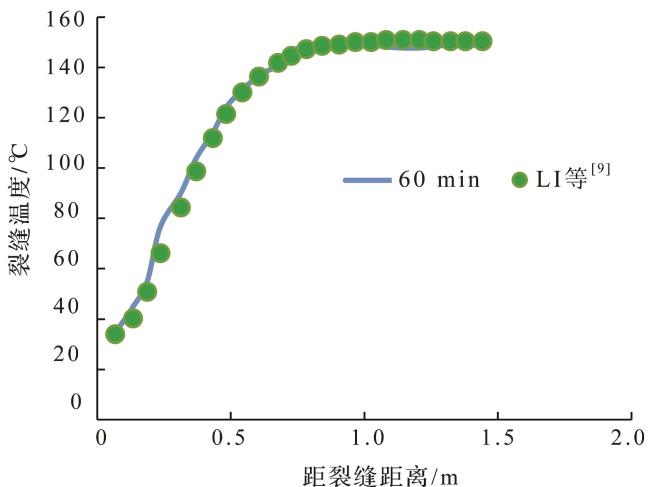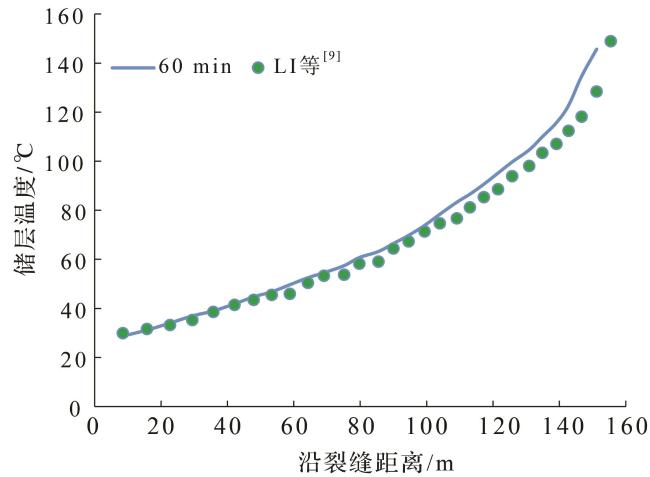朱世琰［8］建立出一套油水两相温度预测模型，预测出了水平井的温度剖面，并通过所测得的温度剖面数据解释了产出剖面，进而确定了出水位置。LI等［9］提出了非稳态数值油藏模型和稳态井筒模型。YOSHIOKA等［10］建立了两相流稳态井筒/油藏热学模型去探测水平井气/水突破位置。该模型耦合了井筒和油藏模型，计算沿井筒的温度变化，在地层中考虑了微热效应。SUI等［11］研究表明如果时间足够长，井筒模型可由非稳态变为稳态。对于水平井，周围地层温度变化相对较小，水平井井筒温度变化主要受热膨胀、黏性耗散和热传导等微热效应所控制。王鸿勋等［12］给出了井筒非稳态传热数值计算模型，其中主要考虑了井筒积液与井筒、水泥环及地层之间的热交换。
从以上研究中可以看出，在水平井温度分布预测方向上，国内外的学者们做了大量相关的研究和实验，但是在定量预测水平井压裂过程中温度分布方面的研究还存在不足。因此，本文建立了一套水平井分段压裂泵注过程中的温度分布预测模型，考虑了多种微热效应的影响，分别建立了井筒模型、裂缝模型及储层模型，并完成模型耦合求解，采用建立的温度模型分别模拟了一口水平井常规压裂和分段多簇压裂时的温度分布，分析了水平井分段压裂过程中的温度分布特征，以及压裂液排量、地层滤失系数对温度分布的影响规律，对于指导水平井分段压裂和改造效果评价具有重要意义。

1 模型建立

建立的温度预测模型包括水平井段井筒模型、裂缝模型和储层模型（图1）。3个模型都含有基于质量守恒建立的渗流模型和基于能量守恒建立的热学模型。分别研究各部分之间的流体交换和热量传递［13］。将建立的水平井段井筒模型、裂缝模型和储层模型进行耦合求解，即可对水平井压裂的温度分布进行预测。
图1 温度预测模型结构

Fig. 1 Structure of temperature prediction model

建立的温度预测模型结构如图1所示：

1.1　水平井段井筒模型

在压裂过程中，压裂液流经井筒进入裂缝，这是一个连续换热过程，射孔孔眼处温度就是裂缝入口初始温度，因此井筒温度场是计算裂缝温度场的基础，必须准确预测井底温度随时间的变化规律。
采用单相井筒流动模型及瞬态井筒热模型，为更新储层和裂缝温度提供信息。

1.1.1　水平井井筒流动模型

YOSHIOKA等［10］提出的生产期质量守恒方程为：
∂ ρ w b ∂ t = 2 γ R ρ l v l - ∂ ρ w b v ∂ y
式中：t为时间，s；R为井筒内径，m； γ为井筒打开程度；ρ l为井筒流入流体密度，kg/m3；v为注入流体在射孔位置流入裂缝的速度，m/s，该速度由井筒流动模型计算，并作为压裂液模型的输入； v l为井筒中注入液速度，m/s；ρ wb为井筒中的流体密度，kg/m3。此外，本文研究的目的是压裂处理，v的方向与生产过程相反。质量平衡方程为：
2 γ R v l - ∂ v ∂ y = 0
井筒流动模型的初始和边界条件：
v i = v t = 0 = 0
v i γ = 0 = 0 v i γ = 1 ≠ 0
式中： v i为射孔位置外压裂进入裂缝的速度，m/s。

1.1.2　水平井井筒热模型

SUI［14］提出的瞬态井筒热模型的最终形式为：
1 v ∂ T ∂ t - β T ρ v C p ¯ ∂ p ∂ t = 2 γ R ρ l v l ρ v ( T 1 - T ) + 2 ( 1 - γ ) R ρ v C p ¯ U T ( T r | r = r w - T ) - ∂ T ∂ z + K J T ∂ p ∂ z - g s i n θ C p ¯
式中：C p为比热容，J/（kg·K）；β为热膨胀系数，1/K；K JT为焦耳—汤姆逊系数，K/MPa；θ为水平井筒倾角，°；g为重力加速度，m/s2；r w，井孔半径，m；U T为综合传热系数，W/（m2·K）；T为注入流体温度，℃； T r为地层岩石温度，℃。对于水基压裂液注入，忽略热膨胀和焦耳—汤姆逊效应［15］，式（5）改写为：
1 v ∂ T ∂ t = 2 γ R ρ l v l ρ v ( T l - T ) + 2 ( 1 - γ ) R ρ v C p ¯ U T ( T r - T ) - ∂ T ∂ y - g s i n θ C p ¯
式中：T l为注入液温度，℃。
初始和边界条件为：
T t = 0 = T w f
T x = 0 , t ≤ t i n j = T w f                  K e ∂ T r ∂ x x = x r e s / w b = U T T r - T
式中：T wf为直井段井底温度，℃；K e是平均有效储层导热系数，J/（ m·s·K）。

1.2　裂缝模型

1.2.1　裂缝流动模型

为了简单起见，对裂缝几何形态进行如下假设：①发生在裂缝处的流体滤失与裂缝面呈线性垂直；②注入过程中裂缝具有无限的导流能力；③压裂液不可压缩。并对裂缝扩展过程进行了建模［16］，裂缝的流动模型为：
2 w h d X f d t = w h v x ( x , t ) - 2 h ∫ 0 2 X f ( t ) C ( t ) t - τ ( x ) d x
式中： τ ( x )为裂缝延伸长度x的时间之后，流体滤失开始；X f为裂缝半长，m；w、h分别为任意微元段的宽和高，m；C为考虑流体压缩性效应C c、流体黏度效应C v和造壁性效应C w的总流体滤失系数。
初始和边界条件为：
X f t = 0 = 0
v x x = R , t ≤ t i n j , γ = 1 = v I X f t ≥ t i n j = C o n s t
式中： t i n j是注入时间，s；裂缝半长在关井过程中保持恒定。

1.2.2　裂缝热学模型

建立了裂缝热学模型［17］，计算了裂缝扩展和关井过程中裂缝内压裂液温度分布。能量守恒的概念与体积微分方程上的裂缝流动模型相似。
ρ l C p l ¯ ∂ T l ∂ t = - ρ l C p l ¯ v x ∂ T l ∂ x - 2 ρ l C p l ¯ v l k T l w + 2 h l ( T r - T l ) w
h 1被定义为牛顿传热系数，由以下方程计算：
h l = N v x s
式中：“—”表示注入流体的性质，以便区分储层和井筒模型；N和s为从实验中获得的无量纲经验常数。
上述式（12）的左端为随时间变化的微分体积能量积累，右端第一项为压裂液流动引起的热对流；第二项为流体损失引起的对流能量损失，最后一项为压裂液与周围环境之间的热传递。
初始和边界条件为：
T l t = 0 = T i
T l x = 0 = T ∂ T l ∂ x x = X f = 0
式中：T i为初始储层温度，℃。

1.3　储层模型

1.3.1　储层流动模型

压裂液从裂缝面向储层滤失的距离可通过将滤失速度与滤失时间相结合来计算。
Y l k ( x ) = ∫ τ ( x ) t v l k d t = ∫ τ ( x ) t C t - τ ( x ) d t
式中： Y l k为压裂液从裂缝面向储层滤失的距离,m； v l k为压裂液从裂缝面向储层滤失的速度,m/s；C为考虑流体压缩性效应C c、流体黏度效应C v和造壁性效应C w的总流体滤失系数。

1.3.2　储层热学模型

为了研究压裂过程中的储层温度，建立了储层热学模型，并与井筒和裂缝模型相结合。根据能量平衡方程推导了局部地层能量守恒方程［18-21］。
ρ C p ¯ ∂ T r ∂ t = - ρ t C p l ¯ v l k ∂ T r ∂ y + ∂ ∂ x K e ∂ T r ∂ x + ∂ ∂ y K e ∂ T r ∂ y
式中： K e为平均有效储层导热系数，J/（m·s·K）；T r为地层岩石温度，℃。
式（17）为局部地层能量守恒方程，对于被压裂液侵入的网格块，其平均有效热容和有效热导率不是恒定的。上述式（17）左端为随时间t在微元段中的能量积累：右端第一项是由于流体滤失进入地层而产生的热转换。第二项和第三项是二维流动系统中的热传导。
初始和边界条件为：
T r t = 0 = T i
∂ T r ∂ x x → ∞ = 0 ∂ T r ∂ y y → ∞ = 0 K e ∂ T r ∂ y y = w 2 = h l T r - T l K e ∂ T r ∂ x x = x r e s / w b = U T T r - T

1.4　耦合模型及求解

为了实时模拟井筒温度分布，将井筒、裂缝和储层模型耦合并结合边界条件进行求解，温度预测模型的求解流程如图2所示。
图2 水平井分段压裂温度分布预测模型求解步骤

Fig.2 Solving steps of temperature distribution prediction model for staged fracturing of horizontal well

2 水平井分段压裂温度分布示例分析

通过模拟一口水平井分段压裂过程中的温度动态，分析水平井分段压裂过程中温度分布特征，并分析压裂液排量、地层滤失系数对温度分布的影响规律，计算示例所需的基本参数如表1所示。
表1 模拟计算所需基础参数

Table 1 Basic parameters required for simulation calculation

参数名称 取值 参数名称 取值
注入时间/s 3 600 总的平均滤失系数/（m/s1/2） 0.020 5
注入速率/（m3/s） 0.023 储层岩石导热系数/［J/（ m·s·K）］ 1.606
裂缝宽度/m 0.006 1 储层流体导热系数/［J/（ m·s·K）］ 0.681 3
裂缝高度/m 45.72 压裂液导热系数/［J/（ m·s·K）］ 0.931 3
模拟时间步长/s 120 储层岩石比热容/［J/（kg·K）］ 845.73
井筒半径/m 0.22 储层流体比热容/［J/（kg·K）］ 4 178.43
储层初始地层温度/℃ 150 压裂液比热容/［J/（kg·K）］ 4 178.43
裂缝流体注入温度/℃ 26.67 储层流体密度/（kg/m3） 420
储层孔隙度（Φ）/% 0.045 压裂液密度/（kg/m3） 993.144
储层岩石密度/（kg/m3） 2 380 — —
如图3和图4所示，分别为该水平井压裂60 min时储层和裂缝中的温度分布，由图可知本文温度模拟结果同LI等［9］模拟的结果吻合度较高，验证了本文建立温度模型的可靠性。
图3 裂缝温度分布对比

Fig.3 Comparison of fracture temperature distribution

图4 储层温度分布对比

Fig.4 Comparison of reservoir temperature distribution

2.1　水平井常规分段压裂

2.1.1　水平井压裂温度分布模拟

在压裂液注入过程中，注入时间对裂缝延伸及温度分布有重要作用，为此，下面给出了该水平井在压裂进行到20 min、40 min及60 min时温度分布特征。
图5所示为单一裂缝在不同注入时间时整个耦合系统的温度，发现随注入时间不断增大，裂缝不断往前延伸，在储层中形成一个“尖锥”，由64 m扩大到138 m左右时，且裂缝四周的滤失距离也随着时间不断向地层扩展，“尖锥”变得越长越宽。通过温度云图还可以看出，随着注入流体在井筒及裂缝中的流动，当流体流入裂缝时，在裂缝跟端位置，温度变化较小，随着流体更进一步的往裂缝中流动，储层也在不断对裂缝中的流体加热使得裂缝中的流体温度不断升高，直至滤失前缘的流体温度与地层温度保持一致。
图5 压裂液注入20 min、40 min、60 min时的水平井压裂温度分布特征

Fig.5 Fracturing temperature distribution cloud map of horizontal well at 20 min, 40 min and 60 min of fracturing fluid injection

2.1.2　温度分布影响规律分析

在压裂过程中，注入流量对裂缝延伸及温度分布具有重要作用，下面给出了注入流量分别为0.018 m3/s、0.023 m3/s及0.03 m3/s，其余的参数保持不变得到的水平井温度分布特征。从图6中可以看出，随着注入流量的增加，则相同时间内进入裂缝中的流量越大，使得裂缝半长更长，滤失距离也更大。
图6 注入流量为0.018 m3/s、0.023 m3/s、0.03 m3/s时的水平井压裂温度分布特征

Fig.6 Fracturing temperature distribution cloud map of horizontal well with injection flow of 0.018 m3/s, 0.023 m3/s and 0.03 m3/s

如前面所述，储层性质对滤失系数有很大影响。当储层中存在天然裂缝时，水力诱发的裂缝已经形成，流体滤失急剧增加，用更高滤失值来表示。考虑到滤失量对裂缝延伸的影响，模拟了不同的滤失系数情况下的温度分布。
从图7中可以看出，滤失系数增大，导致过多压裂液注入地层中，致使滤失距离不断扩大，而裂缝延伸距离不断缩小。
图7 滤失系数为1 Clk、2 Clk、4 Clk时的水平井压裂温度分布特征（1 Clk=3.048×10-5）

Fig.7 Fracturing temperature distribution cloud map of horizontal well with filtration coefficient=1 Clk，2 Clk and 4 Clk （1 Clk=3.048×10-5）

除了注入流量及滤失系数对裂缝半长及温度分布影响有关外，裂缝宽度、裂缝高度对其影响也相对较大。图8所示为不同裂缝宽度时水平井温度分布特征，从图8中可以看出，随着裂缝宽度的增加，在相同的注入流量下，裂缝半长会逐渐降低，滤失距离不断缩短，裂缝中温度会呈现整体的降低。
图8 裂缝宽度（w）为0.006 1 m、0.008 1 m、0.010 1 m时的水平井压裂温度分布特征

Fig.8 Cloud map of fracture temperature distribution cloud map of horizontal well with fracture widths （w）=0.006 1 m, 0.008 1 m and 0.010 1 m

图9所示为不同裂缝高度时水平井温度特征图，从图9中可以看出，随着裂缝高度的增加，在相同注入流量下，裂缝半长会逐渐降低的，裂缝中温度也呈现整体的降低。
图9 裂缝高度(h)为45.72 m、55.72 m、65.72 m时的水平井压裂温度分布特征

Fig.9 Fracturing temperature distribution cloud map of horizontal well with fracture heights (h)=45.72 m, 55.72 m, and 65.72 m

2.2　水平井分段多簇压裂

2.2.1　水平井温度分布模拟

温度预测模型可模拟分段多簇压裂时的温度分布，考虑到多簇裂缝同时扩展。为了研究注入流量对水平井分段多簇压裂温度分布的影响，将总注入量分配到压裂段的每个射孔簇，模拟结果如图10所示，基础参数如表2所示。在理想条件下，段内形成单裂缝时，比段内形成多条裂缝时的温度响应更明显，而段内多簇起裂时，凡是有压裂液注入的位置，储层温度分布上都会形成一个“尖锥”，而“尖锥”的位置，就指示着裂缝起裂位置，对应地，井筒温度剖面中的温降清晰地指示了裂缝起裂的位置，据此，可以通过水平井压裂注液过程中的井筒温度剖面监测，对压裂段内形成的裂缝数量及进行准确诊断。
图10 压裂段内分别形成1条、2条裂缝时的温度分布特征

Fig.10 Cloud map of temperature distribution when 1 and 2 fractures are formed in the fracture stage

表2 注入流量与裂缝半长

Table 2 Injection flow rate and fracture half-length

簇号 注入速率/（m3/s） 裂缝间距/m 裂缝半长/m
1 0.03 0 84.13
2 0.03 4.2 42.06

2.2.2　温度分布影响规律分析

下面对分段多簇压裂时的温度分布进行研究，假设单段注入流量为0.064 m3/s。段内分4簇，各簇注入量及其裂缝参数如表3所示。
表3 各射孔簇注入流量与裂缝半长

Table 3 Injection flow rate and fracture half-length of each perforation cluster

簇号 注入速率/（m3/s） 裂缝半长/m
1 0.015 42.06
2 0.015 42.06
3 0.017 48.93
4 0.017 48.93

注：单阶段注入速率为0.064 m3/s

图11—图12为分段多簇压裂时单段内多条裂缝同时起裂时水平井温度云图，当4条裂缝注入量相等时，则4条裂缝的裂缝半长及滤失距离都保持相等，各级裂缝对应的温度分布基本一致；当各射孔簇注入量不相等时（图12），进液量大的射孔簇裂缝半长越大，温度响应范围也越大，而温度响应的波及范围，也就很好地指示了压裂液在地层中的分布。
图11 4条裂缝注入量相等水平井温度分布特征（0.016 m3/s）

Fig. 11 Temperature distribution cloud map of horizontal well with the same injection amount of four fractures （0.016 m3/s）

图12 4条裂缝注入量不相等水平井温度分布特征

Fig.12 Temperature distribution cloud map of horizontal well with different injection amount of four fractures

3 结论

（1）本文在考虑多种微量热效应的基础之上，建立了一套水平井分段压裂注液过程中的温度分布预测模型，并完了耦合求解，实现了水平井分段压裂注液过程中的温度分布动态模拟预测。
（2）采用建立的温度模型模拟分析了水平井常规分段压裂和分段多簇压裂注液过程中的温度动态，结果表明，在水平井水力压裂注入过程中，在裂缝起裂位置，储层温度分布会形成一个“尖锥”，且裂缝四周的滤失距离也随着时间不断向地层扩展，导致“尖锥”变得越长越宽。
（3）水平井压裂段内形成单裂缝时，比段内形成多条裂缝时的温度响应更明显；段内多簇起裂时，储层温度分布上都会形成多个“尖锥”，而每一个“尖锥”就对着一条张开裂缝，据此特征可对压裂段内形成的裂缝数量和位置进行准确诊断。
（4）随着压裂液注入时间的不断增长，井筒温度剖面在起裂位置的温降也越大，为了定量描述裂缝半长与温降的联系，可以通过DTS测量压裂注液过程中动态温度数据，从而进行裂缝诊断，如裂缝位置识别、裂缝半长大小。

References

Publishing order | Descend order by publishing year | Descend order by cited within
1
黄尚廉， 粱大巍， 骆飞.分布式光纤传感器现状与动向［J］. 光电工程， 2000， 17（3）： 57-62.

HUANG S L，LIANG D W， LUO F. Present situation and trend of distributed optical fiber sensors［J］. Optoelectronic Co-mponent， 2000， 17（3）： 57-62.

2
BARNOSKI M K. Optical time domain reflecometer［J］.Applied Opticals，1977，16（9）：2375-2379.

3
罗红文， 李海涛， 刘会斌， 等.低渗气藏两相渗流压裂水平井温度剖面预测［J］. 天然气地球科学，2019，30（3）：389-399.

LUO H W， LI H T， LIU H B， et al. Temperature profile prediction of fractured horizontal well with two-phase seepage in low permeability gas reservoir［J］. Natural Gas Geoscience， 2019， 30（3）： 389-399.

4
罗红文， 李海涛， 蒋贝贝， 等.基于DTS数据反演的低渗气藏压裂水平井产出剖面解释新方法［J］. 天然气地球科学， 2019， 30（11）： 1639-1645.

LUO H W， LI H T， JIANG B B， et al. A new method for production profile interpretation of fractured horizontal well in low permeability gas reservoir based on DTS data inversion［J］. Natural Gas Geoscience， 2019， 30（11）： 1639-1645.

5
LUO H W， LI Y， LI H T， et al. A simulated annealing algorithm-based inversion model to interpret flow rate profiles and fracture parameters for horizontal wells in unconventional gas reservoirs［J］. SPE Journal，2021，26（4）：1679-1699.

6
LUO H W， LI H T， TAN Y S， et al. A novel inversion approach for fracture parameters and inflow rates diagnosis in multistage fractured horizontal wells［J］. Journal of Petroleum Science and Engineering， 2020， 184：106585.

7
罗红文， 李海涛， 李颖，等.分段压裂水平井温度分布预测模型研究［J］. 科学技术与工程，2020，20（29）：11915-11922.

LUO H W， LI H T， LI Y， et al. Research on temperature distribution prediction model of staged fractured horizontal well［J］. Science Technology and Engineering，2020，20（29）： 11915-11922.

8
朱世琰. 基于分布式光纤温度测试的水平井产出剖面解释理论研究［D］. 成都：西南石油大学，2016.

ZHU S Y. Theoretical Study of Horizontal Well Production Profile Interpretation Based on Distributed Optical Fiber Temperature Measurement［D］. Chengdu：Southwest Petroleum University， 2016.

9
LI Z， ZHU D. Predicting flow profile of horizontal well by downhole pressure and DTS data for water-drive reservoir［J］. SPE Production & Operations，2012， 25 （3）： 296-304.

10
YOSHIOKA K， ZHU D， HILL A D， et al. Prediction of temperature changes caused by water or gas entry into a horizontal well［J］. SPE Production & Operations，2007，22（4）：425-433.

11
SUI W， ZHU D， HILL A D， et al. Model for Transient Temperature and Pressure Behavior in Commingled Vertical Wells［C］. SPE 115200 Presented at SPE Russian Oil and Gas Technical Conference and Exhibition， Moscow， Russia， 2008.

12
王鸿勋， 李平.水力压裂过程中井筒温度的数值计算方法［J］. 石油学报，1987，8（2）：91-99.

WANG H X， LI P. Numerical calculation method of wellbore temperature during hydraulic fracturing［J］. Acta Petrolei Sinica，1987，8（2）：91-99.

13
LUO H W， LI H T， ZHOU X J， et al. Modeling temperature behavior of multistage fractured horizontal well with two-phase flow in low-permeability gas reservoirs［J］.Journal of Petroleum science and Engineering， 2019，1187-1209.

14
SUI W. Determining multilayer formation properties from transient temperature and pressure measurements［J］. Petroleum Science and Technology，2012，30（7）：65-66.

15
KAMPHUIS H， DAVIES D R， ROODHART L P. A new simulator for the calculation of the in situ temperature profile during well stimulation fracturing treatments［J］. Journal of Canadian Petroleum Technology， 1993， 32（5）： 38-47.

16
DAWKRAJAI P， LAKE L W， YOSHIOKA K， et al. Detection of Water or Gas Entries in Horizontal Wells from Temperature Profiles［C］. SPE 100050 Presented at SPE/DOE Symposium on Improved Oil Recovery， Tulsa， Oklahoma， 2006.

17
LUO H W， LI H T， LI Y H， et al. Investigation of temperature behavior for multi-fractured horizontal well in low-permeability gas reservoir［J］. International Journal of Heat and Mass Transfer，2018，127：375-395.

18
TABATABAEI M， ZHU D. Fracture-stimulation diagnostics in horizontal wells through use of distributed-temperature-sensing technology［J］. SPE Production & Operations， 2012， 27（4）： 356-362.

19
PINZON I D， DAVIES J E， MAMMADKHAN F， et al. Monitoring Production From Gravel-Packed Sand-Screen Completions on BP's Azeri Field Wells Using Permanently Installed Distributed Temperature Sensors［C］.Paper SPE 110064 Presented at the SPE Annual Technical Conference and Exhibition， 2007.

20
SETH G， REYNOLDS A C， MAHADEVAN J. Numerical Model for Interpretation of Distributed-Temperature-Sensor Data During Hydraulic Fracturing［C］. SPE Annual Technical Conference and Exhibition， 2010.

21
LUO H W， JIANG B B， LI H T， et al. Flow rate profile interpretation for a two-phase flow in multistage fractured horizontal wells by inversion of DTS data［J］. ACS Omega，2020， 5（34）：21728-21744.

Options
Outlines

/

〈 〉

陇ICP备2021001824号-7　 甘公网安备 62010202000678号
Copyright © Natural Gas Geoscience, All Rights Reserved.
Tel: (0931)8277790　
E-mail：geogas@lzb.ac.cn
Total visitors:　 Visitors of today: 　 Now online:
Powered by Beijing Magtech Co. Ltd,.