Natural Gas Geoscience >

2021 , Vol. 32 >Issue 3: 423 - 436

DOI: https://doi.org/10.11764/j.issn.1672-1926.2020.12.010

Pore structure characteristics of low-rank coal reservoirs and evaluation of fractal models

  • Teng-fei JIA , 1 ,
  • Meng WANG , 1, 2 ,
  • Xing-yue GAO 3 ,
  • Jian-guang ZHAO 1 ,
  • Jun-qing ZHU 1
Expand
  • 1. School of Geology and Mining Engineering，Xinjiang University，Urumqi 830047，China
  • 2. Key Laboratory of Coalbed Methane Resources and Reservoir Formation Process of the Ministry of Education，China University of Mining and Technology，Xuzhou 221008，China
  • 3. Yungang Coal Mine of Datong Coal Mine Group, Datong 037000, China

Received date: 2020-09-25

  Revised date: 2020-12-12

  Online published: 2021-03-22

Supported by

The Key Project of Joint Funds of the National Natural Science Foundation of China(U1903209)

The Natural Science Foundation of Xinjiang Uygur Autonomous Region(2018D01C062)

The Fundamental Research Funds for the Central Universities(2020ZDPYMS09)

Fold

Highlights

The configuration of the pore structure of the coal plays a vital role in the adsorption of coalbed methane. The fractal model has a good description in characterizing the roughness of the coalbed surface and the complexity of the pore structure. In order to explore the pore structure and fractal characteristics of the southeastern margin of the Junggar Basin， based on mercury injection experiment and low-pressure nitrogen adsorption， the pore structure of coal samples from different mines in the southeast of Junggar Basin were tested， the fractal characteristics of pores with different scales were analyzed， and the comprehensive characterization method for multi-scale fractal features of coal pore structures was discussed. The applicability of different models from different angles was studied. The results show that： the Menger model， the Capillary model， the Sierpinski model based on mercury injection data and FHH model based on N2 adsorption data can effectively characterize the pores with different scales. By establishing the comprehensive fractal dimension （D t）， combining mercury injection and low-pressure nitrogen adsorption models according to coal porosity， coal seam permeability and physical properties to compare the advantages and disadvantages of different factors for different modes， the Sierpinski model is preliminarily determined as the optimal model.

Cite this article

Teng-fei JIA , Meng WANG , Xing-yue GAO , Jian-guang ZHAO , Jun-qing ZHU . Pore structure characteristics of low-rank coal reservoirs and evaluation of fractal models[J]. Natural Gas Geoscience, 2021 , 32(3) : 423 -436 . DOI: 10.11764/j.issn.1672-1926.2020.12.010

0 引言

煤中孔隙大小不同、形态各异，不同类型的孔在煤层气的运移以及富集的过程中起着不同的作用［1-2］，不同尺度的孔对煤层气吸附解析、扩散和渗流的控制有所不同［3］。气体在煤中主要以扩散和渗流的方式移动，通常情况下孔径小的孔在连通性和运移能力等方面的表现有所欠佳但具有较高的比表面积，故通常可提供较多的吸附位，决定煤层气吸附能力的强弱；孔径适度的孔主要作为缓慢渗流孔，气体在其中发生稳定的、缓慢的层流；孔径较大的孔由于孔径大，气体分子在运移过程中发生强烈的层流或紊流，故作为强烈或剧烈渗流孔［4-7］。
分形理论的出现为了解煤层气在不同尺度、不同类型孔中的运移规律以及孔隙结构的定量表征提供了有效手段［8-9］，国内外研究学者对此做了大量的研究。傅雪海等［4］基于压汞实验分形特征对煤孔隙结构分类提出了新的方案；PFEIFER等［10］提出岩石孔隙具有分形的性质；CAI等［11］和YAO等［12-13］基于压汞法建立了煤层分形理论模型。
准噶尔盆地东南缘是我国低阶煤的主要分布区域，众多学者对该区的煤层气富集模式［14］、有利优选区［15］、沉积构造［16］等进行了研究，但对低阶煤储层的孔隙结构特征研究少，特别是在定量表征孔隙结构参数、连通性以及分形特征等方面。
为此，以准东南西山窑组和八道湾组地层作为研究对象，采集了硫磺沟煤矿、碱沟煤矿、将军庙煤矿以及呼图壁煤矿4个矿区的煤样，采用压汞法和液氮法对样品的孔隙特征和分形特征进行研究，以深化准东南地区煤的孔隙性研究。

1 样品实验与方法

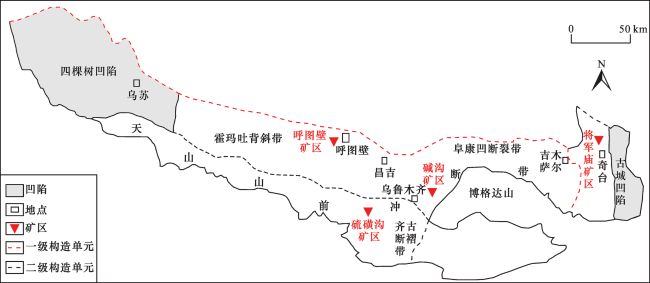
1.1　地质背景

准噶尔盆地东南缘位于准噶尔盆地与北天山的交互部位。先后经历了海西运动、印支运动、燕山运动和喜马拉雅运动4期大型构造活动的改造，最终构成大型前陆盆地［17］。准噶尔盆地作为煤层气重点勘探区，现有阜康矿区日产最高井可达1.71×104 km3，且通过准南玛纳斯矿区、硫磺沟矿区等和准东白家海矿区等作对比（图1），可以发现，不同矿区的主力煤层主要为侏罗系中统西山窑组（J2 x）和下统八道湾组（J1 b），以八道湾组发育的湖泊三角洲沉积和西山窑组发育的三角洲沉积为特征，为煤层富集奠定基础［18］。整体煤层演化程度不高，但分布稳定，厚度大，主要埋深为380~1 200 m，平均含气量可达4.13~11.78 m3/t［19-21］。
图1 研究区构造示意

Fig.1 Tectonic division map of the research area

1.2　实验方案

研究采集样品均来自准东南地区4个矿区，包括硫磺沟煤矿、碱沟煤矿、将军庙煤矿以及呼图壁煤矿，样品数量共计5个，编号分别为LH（1＃）、JG43（2＃）、JG45（3＃）、JM（4＃）、HT（5＃）。对采集的样品进行显微组分、工业组分、高压压汞试实验和低温液氮实验测试。本文受限于篇幅，样品的基础参数测试结果见表1。
表1 煤岩参数

Table 1 The coal petrologic parameters

煤样 显微组分/%

镜质组反射率

/%

水分

/%

灰分

/%

挥发份

/%

固定碳

/%

镜质组 壳质组 惰质组
1＃ 62.86 4.56 32.57 0.86 9.64 3.87 25.97 77.16
2＃ 73.89 7.93 14.18 0.55 2.81 5.19 41.01 55.93
3＃ 74.62 8.53 16.85 0.78 2.34 3.1 31.64 66.24
4＃ 66.74 6.49 26.78 0.62 16.73 3.91 33.06 64.33
5＃ 77.49 7.22 15.29 0.8 5.32 2.52 28.82 69.39

注：水分（Mad）为空气干燥基；挥发份（Vdaf）为无灰基；灰分（Ad）为干燥基；固定碳（FCd）为干燥基

显微组分采用Axio Scope.A1型显微光度计，测试标准依据国家标准（GB/T 6948—2008）和（GB/T 8899—2013）；工业组分采用XL—2000型号马弗炉，测试标准依据国家标准（GB/T 212—2008）；孔隙度和渗透率采用AO-608型覆压孔隙度—渗透率仪，测试标准依据行业标准（SY/T 6395—2016）；高压压汞实验采用AutoPore9500压汞仪，测试标准依据国家标准（GB/T 21650.1—2008），孔径的测量范围在3 nm~1 000 μm之间；低温液氮实验采用TriStar3020型低温氮吸附仪，测试标准依据国家标准（GB/T 21650.2—2008）。以上实验均在贵州煤田地质局进行。

2 结果与讨论

2.1　孔隙结构特征

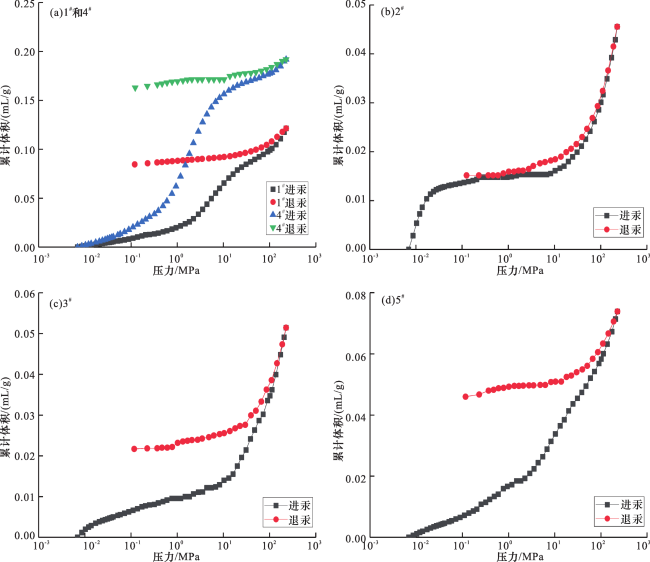
孔隙结构参数是反映煤储层的吸附性、渗透性的重要参数，主要包括孔隙的连通性、孔容、孔比表面积及孔径分布等等。本文采用霍多特煤岩分类，将煤岩孔隙分为4类：大孔V 1（>1 000 nm）、中孔V 2（100~1 000 nm）、过渡孔V 3（10~100 nm）、小孔V 4（<10 nm）。

2.1.1　高压压汞测试分析

高压压汞实验是常用表征煤层孔隙连通性、结构复杂度以及孔隙的发育情况的一种手段［22］。煤样的进退汞曲线见图2，可以得出，不同样品之间的进退汞曲线不尽相同，但均呈现滞后环现象。对研究区岩心样的进退汞曲线及孔径分布进行分析，研究区压汞曲线分为4类［23-25］。Ⅰ类［图2（a）］显示随着压力的增加，在压力较低时，随着注汞压力的增大进汞量明显增多，且进退汞曲线开口大，滞后明显，说明相对孔径段中的开放孔多，连通性好。Ⅱ类［图2（d）］显示随着进汞压力的不断增加，进汞曲线持续上升，说明各尺度的孔隙均有分布，且以开放孔为主，连通性较好。Ⅲ类［图2（b）］显示进退汞曲线斜率差别不大，滞后环不明显，表明孔隙以半开放孔为主，连通性差。Ⅳ类［图2（c）］显示进退汞曲线斜率在高压时相似，在低压时退汞曲线滞后，说明小孔段连通性差，大孔段连通性好。
图2 进退汞曲线

Fig.2 Mercury intrusion and ejection experiment curves

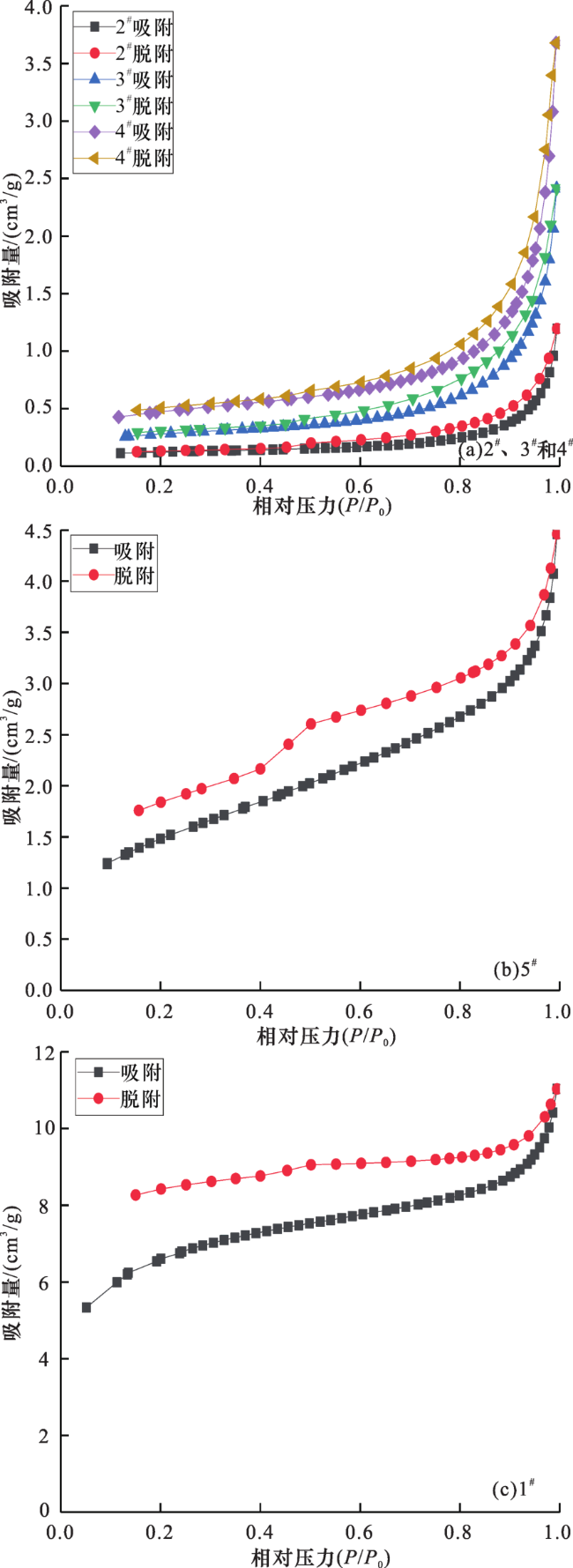
2.1.2　低温液氮吸附测试

由于高压压汞实验在测试小孔径受限制，无法进行针对性的表征，故本次研究针对此不足开展液氮吸附实验，将50 nm以下的孔隙用低温液氮测试的方法表征，以期对孔径进行全尺度的覆盖，精确表征样品的孔隙性。根据不同吸附脱附曲线的类型可以断定不同孔隙的特点，煤样的吸附脱附曲线见图3，可以得出，样品的吸附曲线和脱附曲线形态有差异，但均形成滞后环现象。通过对比IUPAC对滞后环的分析，研究区吸附脱附曲线分为3类：Ⅰ类如图3（a）所示，与H3型相似，但同时具有H4型部分特征，主要表现为在饱和压处吸附脱附曲线陡峭，形成的滞后回线狭小，表明孔隙以狭缝状孔、平行板状孔和楔状半封闭孔为主，吸附曲线主要表现为前段缓慢上升，后段剧烈上升，表明孔隙中含有一定量的大孔和中孔。Ⅱ类如图3（b）所示，与H2型相似，但同时具有H4型部分特征，主要表现为脱附曲线在压力适中时有一个骤降，说明其突破瓶颈作用，表明孔隙中含有墨水瓶孔等，吸附曲线较Ⅰ类相比更加平滑，表明孔隙中含有一定量的微—中孔。Ⅲ类如图3（c）所示，与Ⅱ类相比，主要表现为脱附曲线在压力全程下降平稳，产生滞后回线明显，表明孔隙中以墨水瓶孔为主，吸附曲线主要表现为相对压力较小时上升快速，相对压力适中时上升缓慢，相对压力较大时上升迅速，表明孔隙中含有一定量的微孔。
图3 吸附—解吸曲线

Fig.3 Adsorption and desorption curves

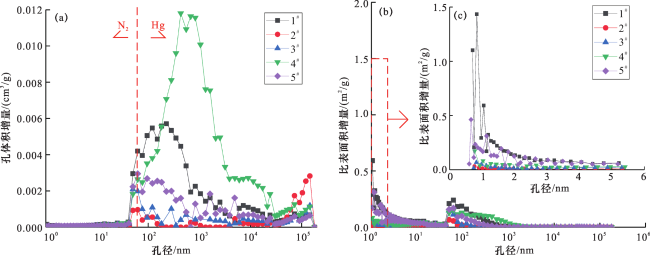
2.1.3　多种实验联合表征全尺度孔径分布

基于以上研究，本文对高压压汞以及液氮吸附实验测试结果进行综合表征，考虑到不同实验的优劣性不同，故将最优段孔径结果进行叠加，将大孔、中孔和部分过渡孔（>50 nm）孔容和孔比表面积采用高压压汞实验测试结果；部分过渡孔（<50 nm）和小孔采用低温液氮实验测试结果。联合不同实验，探讨不同样品的优势孔径区间和孔比表面积的贡献度（表2，图4），研究结果如下，4类孔隙对孔容均有所贡献，其中不同样品中大孔、中孔、过渡孔和小孔体积分别占总孔体积的25.66%~78.64%、6.48%~52.11%、6.39%~25.31%、0.46%~4.27%，且中孔和大孔的贡献最明显。相较于比表面积而言，则以小孔和部分过渡孔贡献明显，大孔、中孔、过渡孔和小孔比表面积占总比表面积的0.25%~3.61%、4.64%~32.42%、11.45%~41.62%、37.59%~80.92%。由此可知，煤样中大量吸附点位是由小孔和部分过渡孔提供，而孔隙空间主要由中孔和大孔提供。
表2 孔隙结构参数

Table 2 The parameter of pore structure

煤样编号 孔容/(mL/g) 比表面积/(m2/g)
V 1 V 2 V 3 V 4 S 1 S 2 S 3 S 4
1＃ 0.021 6 0.043 9 0.015 4 0.003 4 0.021 9 0.671 2 0.999 3 7.036 6
2＃ 0.014 9 0.001 2 0.002 6 0.000 2 0.001 7 0.023 2 0.208 4 0.267 3
3＃ 0.009 6 0.004 4 0.004 9 0.000 6 0.003 8 0.072 1 0.430 3 0.682 5
4＃ 0.072 2 0.084 3 0.010 7 0.000 8 0.101 3 0.909 1 0.739 4 1.054 1
5＃ 0.017 2 0.016 6 0.009 0 0.001 9 0.015 0 0.275 6 0.616 1 3.844 6

注： V 1、V 2、V 3、V 4分别为大孔、中孔、过渡孔和小孔孔容；S 1、S 2、S 3、S 4分别为大孔、中孔、过渡孔和小孔孔比表面积

图4 阶段进汞量和孔比表面积变化关系

（a） 阶段进汞量； （b）比表面积增量；（c） b局部放大

Fig.4 The relationship between stage mercury intrusion and surface area

2.2　孔隙分形特征

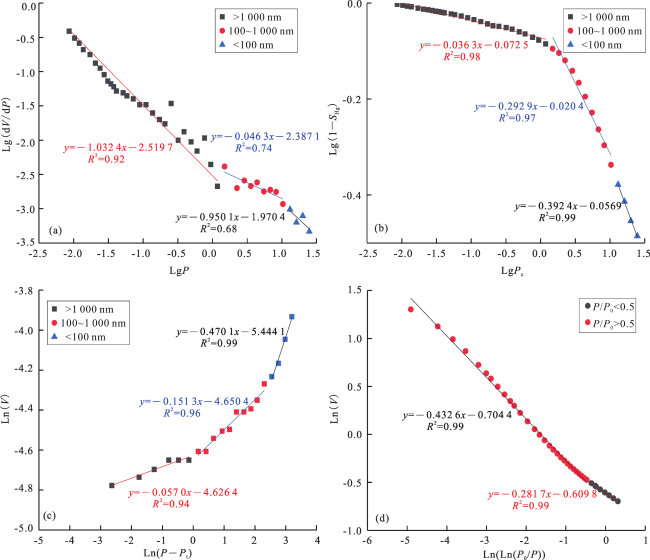
2.2.1　孔隙分形模型理论

分形的概念始于1973年MANDELBORT等［26］提出，标尺不变性即对于一个物体无论将其放大或缩小，用于表征该物体的表面复杂程度和结构形态等特征的分形不会发生明显的变化［27］。本文研究对象为低阶煤，根据煤的非均质性和孔隙分布情况的不同，在建立分形模型和研究时，应根据实际孔径分布情况进行不同尺度的分形研究［28］。
本文研究样品的阶段进汞量的变化范围和趋势具有不完全相似性（图2，图3），故不能够对不同样品采取整体回归的方法研究其分形特征，因此本文就不同尺度分别讨论不同分形模型的分形特征，最后就综合分形维数探讨不同模型的适用性。

2.2.2　孔隙分形模型

(1)Menger海绵模型。将多孔材料假设是一个规则的立方体，通过用统一半径为r的球体填充该立方体，通过填充的小球数目与压汞实验（小球半径r与进汞压力P）的关联［29］，进而得出如下模型：
L g d V d P ∝ D m - 4 L g P
式中：V为进汞量，mL/g；P为进汞压力，MPa；K为幂指数，无量纲。
通过得出对数函数Lg［dV/dP］和LgP的斜率K，分形维数Dm=4+K。
(2)毛细管模型。利用毛细管模型的本质，即孔径与毛细管压力之间的关系，结合几何学原理，通过其余进汞饱和度的关系［30］，进而得出如下模型：
L g   ( 1 - S H g ) = 3 - D c L g P s + D c - 3 L g P c
式中：S Hg为进汞饱和度，%；LgP c为毛细管压力，MPa；LgP s为入口毛细管压力，MPa。
通过得出对数函数Lg（1－S Hg）和LgP c的斜率K，分形维数D c=3+K。
(3)Sierpinski模型。利用地毯模型的建立，即通过将一个正方体划分为9等分体积的小正方体，去除中心的一个正方体，将剩下的正方体反复做此操作，迭代n次之后形成［31］。通过压力和进汞量的关系，进而得出如下模型：
L n V = L n α + ( 3 - D s ) L n ( P - P t )
式中：V为进汞量，mL/g；α为常数，无量纲；P为压力，MPa；P t为门限压力，MPa。
通过得出对数函数Ln（V）和Ln（P－Pt）的斜率K，分形维数D s=3－K。
(4)FHH模型。FHH模型是由PFEIFER等［10］提出，常被应用于表征计算煤种尺度小的孔的分形特征，具有适用性广，模型简单等特点，通过吸附量和压力的关系，进而得出如下模型：
L n V = K L n L n   P 0 P + C
式中：V为气体吸附量，cm3/g；K为斜率，无量纲；P为气体吸附的平衡压力，MPa；P 0为饱和蒸汽压力，MPa。
通过得出对数函数Ln（V）和Ln（Ln（P 0 /P））的斜率K，分形维数D f=3+K。

2.2.3　分形特征

本文通过对样品进行综合分析，分别建立以上4种模型，前三者针对压汞实验中孔径大于50 nm的孔隙进行分析，分段依据拐点，后者针对液氮实验中孔径小于50 nm孔隙进行分析，分段依据不同压力段。通过不同模型的分形维数以及相关关系进一步确定孔隙分形特征（表3）。
表3 煤岩分形维数计算统计

Table 3 Calculation of fractal dimension of coal sample tables

煤样 孔径(d)/nm 相关系数（R 2） 分形维数（D m） 相关系数（R 2） 分形维数（D c） 相关系数（R 2） 分形维数（D s） 相关系数（R 2） 分形维数（D f）
1＃ d≥1 000 0.92 2.968 0 0.98 2.963 7 0.98 2.769 7
100<d≤1 000 0.71 3.520 7 0.97 2.707 1 0.99 2.464 1
50≤d<100 0.94 2.385 8 0.99 2.607 6 0.99 2.768 9
24≤d<50 0.98 2.839 9
d<24 0.99 2.919 8
2＃ d≥1 000 0.92 2.267 9 0.81 2.968 4 0.80 2.994 8
100<d≤1 000 0.80 3.249 9 0.52 2.990 4 0.52 2.982 7
50≤d<100 0.82 3.826 8 0.97 2.867 5 0.98 2.794 9
24≤d<50 0.99 2.742 3
d<24 0.99 2.524 9
3＃ d≥1 000 0.96 2.798 4 0.99 2.963 9 0.94 2.943 0
100<d≤1 000 0.27 3.247 1 0.95 2.950 9 0.96 2.848 7
50≤d<100 0.68 3.587 7 0.97 2.765 1 0.99 2.529 9
24≤d<50 0.99 2.705 7
d<24 0.98 2.542 3
4＃ d≥1 000 0.96 3.417 7 0.88 2.921 9 0.94 2.781 9
100<d≤1 000 0.98 2.399 6 0.99 2.405 6 0.96 2.721 6
50≤d<100 0.95 2.224 5 0.99 2.606 7 0.99 2.934 0
24≤d<50 0.99 2.718 3
d<24 0.99 2.567 4
5＃ d≥1 000 0.92 2.967 6 0.97 2.949 2 0.98 2.748 8
100<d≤1 000 0.74 3.953 7 0.94 2.829 1 0.98 2.673 6
50≤d<100 0.68 3.049 9 0.99 2.659 7 0.99 2.714 1
24≤d<50 0.99 2.620 6
d<24 0.98 2.836 9

注： D m为Menger海绵模型分形维数；D c为毛细管模型分形维数；D s为Sierpinski模型分形维数；D f为FHH模型分形维数

在Menger海绵模型中［图5（a）］，通过双对数曲线LgP与Lg（dV/dP）之间的关系，可以看出不同孔径对应的曲线拟合关系不同。除4＃样品以外，其余井的样品大孔的孔隙整体分形维数均小于3且相关系数高，均在0.92以上。中孔和部分过渡孔的孔隙分形维数基本均大于3，相关系数有高有低，整体介于0.27~0.94之间。在4＃样品中，样品大孔的孔隙分形维数为3.417 7，相关系数高，为0.96。中孔和部分过渡孔的孔隙分形维数为2.399 6、2.224 5，相关系数为0.98、0.95。分形理论普遍认为分形维数的变化区间在2~3之间，对于出现分形维数大于3的原因，不同学者针对这一情况已形成统一的认识［32-35］。首先是煤本身是一个多孔物质具备疏松的特性，其次在高压条件下，可能造成煤样的压缩，而煤样压缩进而导致内部孔隙、裂隙等的压缩性发生改变甚至破坏，致使其分形维数大于3。综上所述，在Menger海绵模型的基础上，本文实验主要反映了煤中大孔的分形特征，从孔隙形态上进行了表征其分形特征。
图5 不同模型分形维数计算图解

（a） Menger海绵模型（5#）； (b)毛细管模型（1#）； (c) Sierpinski模型（3#）； (d) FHH模型（4#）

Fig.5 The fractal dimension of different models

在毛细管模型［图5（b）］和Sierpinski模型［图5（c）］中，通过双对数曲线之间的关系，得出样品大于50 nm孔隙的分形维数均小于3，前者介于2.405 6~2.990 4之间，后者介于2.464 1~2.994 8之间，整体反映出D c>D s；二者相关系数均有浮动，前者介于0.52~0.99之间，但只有一例相关系数小于0.8，2/3的样品相关系数大于0.9，后者介于0.52~0.99之间，但有86%的样品相关系数大于0.94，只有两例相关系数小于90%。综上所述，以上2种模型均能较好地表征煤层不同尺度孔隙的分形特征，两者之间的对比将在后续研究进一步划分。
在FHH模型中［图5（d）］，通过双对数曲线LnV与Ln（Ln（P 0 /P））之间的关系，得出样品部分过渡孔和小孔分形维数均小于3，介于2.524 9~2.919 8之间，相关系数极高，介于0.98~0.99之间。表明在研究区中，FHH模型能很好地表征煤层不同尺度孔隙的分形特征。

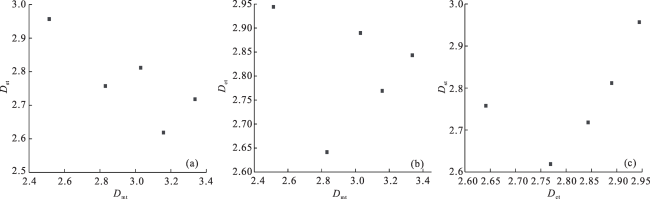
2.3　不同分形维数的分析

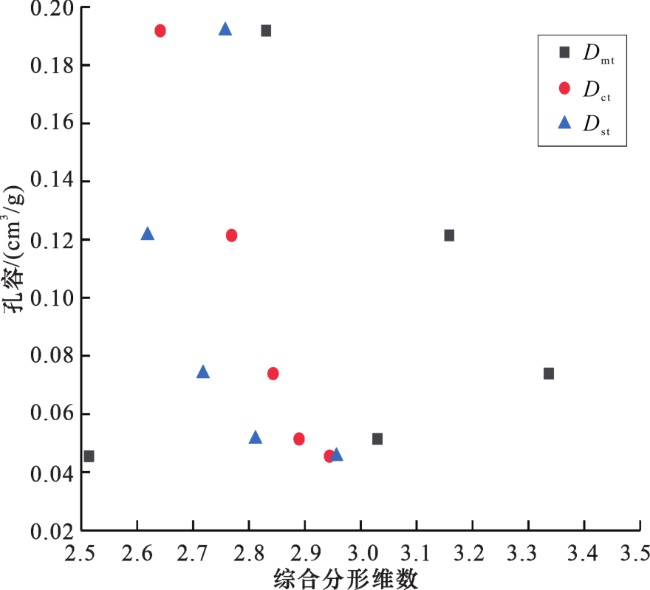
2.3.1　分形维数与孔隙结构

通过以上3种模型的建立，为了方便不同模型分形维数之间作对比，本文引入综合分形维数进行分析，原理是将不同分形维数按照孔隙的占比，使分散的分形维数形成一个总体分形维数，对不同孔径的分形维数做加权平均，进而得到煤样总体的综合分形维数，公式如下：
D t = ∑ D i T i
式中：D t为综合分形维数，无量纲；Di为各孔径的分形维数，无量纲；Ti为各孔径的体积占比，%。
通过综合分形维数的建立（表4），使得3种模型在表征不同尺度孔隙分形特征上具有了统一的标准。结合综合分形维数与孔容增量的关系（图6），可以得出：在Menger海绵综合模型中，通过对孔隙体积分形的表征，随着分形维数的增加，孔容整体呈现出减小的趋势，表明孔隙的复杂程度和粗糙程度孔隙的空间变化有影响。在毛细管模型中，随着分形维数的增加，孔容有减小的趋势，表明随着孔隙结构的复杂化孔隙的空间变小，直接反映了孔隙复杂性影响着孔隙空间的变化。Sierpinski综合模型与毛细管综合模型变化趋势一致，随着分形维数的增加孔容减小，结合上文对于孔隙的探讨，研究区煤样基本以大孔和中孔为主，毛细管综合模型相较于Sierpinski综合模型而言对中孔孔隙的表征更好，Sierpinski综合模型对全孔径的表征最好。但是就孔隙的表征而言，毛细管综合模型和Sierpinski综合模型是否具更好的适用性有待进一步考证。
表4 不同模型综合分形维数

Table 4 Comprehensive fractal dimension of different models

煤样 综合分形维数(D mt) 综合分形维数(D ct) 综合分形维数(D st)
1＃ 3.158 4 2.769 1 2.618 7
2＃ 2.513 8 2.944 3 2.956 7
3＃ 3.029 9 2.889 9 2.811 7
4＃ 2.830 9 2.641 5 2.757 6
5＃ 3.336 6 2.843 4 2.718 1

注： D mt为Menger海绵模型综合分形维数；D ct为毛细管模型综合分形维数；D st为Sierpinski模型综合分形维数

图6 分形维数与孔容的关系

Fig.6 The relationship between fractal dimension and pore volume

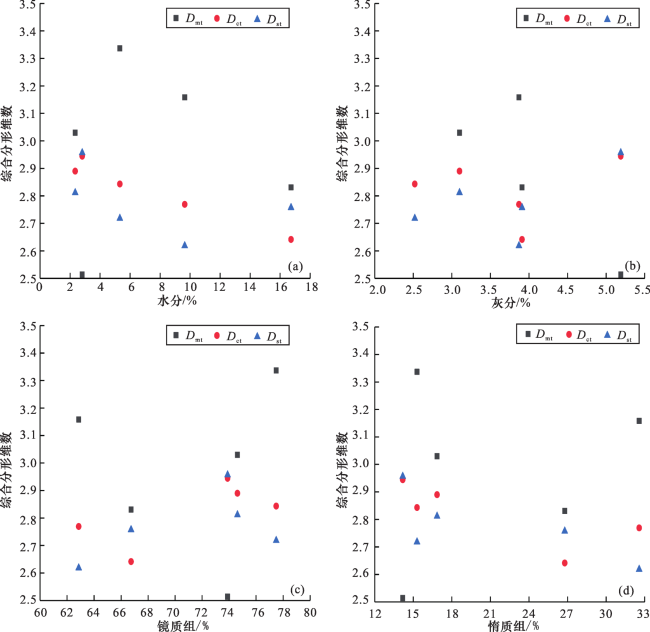
2.3.2　分形维数与储层物性

在一定程度上，综合分形维数表征不仅反映了孔隙的程度而且表征了煤体表面的复杂程度，其中煤岩煤质组分在一定程度上与分形维数的变化存在联系。张松航等［36］在理论上得出随着煤的变质程度的增加，煤中的水分会逐渐减少进一步导致水分被充填从而使分形维数降低。从图7（a）可以得出，当水分含量较低时，不同模型的分形维数均较大，随着水分的增加，呈现不同的趋势。但是在水分含量较低时，随着水分的增加，煤体表面不平整的地方被水分充填，导致煤体表面光滑，分形维数变小，当水分到达一定程度时，随着水分的增加，会使煤中孔隙结构变复杂，致使分形维数的增加。Sierpinski综合模型很好地反映了这一特性，Menger海绵综合模型和毛细管综合模型就这一特性反映不明显，表明模型对水分的考虑有待欠缺。
图7 分形维数与储层物性的关系

（a） 水分与综合分形维数； （b） 灰分与综合分形维数； （c） 镜质组与综合分形维数； （d） 惰质组与综合分形维数

Fig.7 The relationship between fractal dimension and reservoir of physical property

灰分主要通过影响煤中孔隙的发育进一步影响分形维数。王有智［37］通过实验得出灰分在含量较低时灰分颗粒可充填在孔隙喉道和微孔中，造成分形维数变小，非均质性增强。从图7（b）中可以看出，当灰分小于4%时，矿物可以充填在煤体孔隙，导致表面的粗糙度和孔隙的复杂度减小，毛细管综合模型和Sierpinski综合模型的分形维数会随着灰分的增加而降低，当超过4%时，随着矿物的不断充填导致煤样表面的粗糙度和孔隙的复杂度增加，分形维数随着灰分的增加而增加，而Menger海绵综合模型就这一特性反映不明显，表明该模型对灰分的考虑有所欠缺。
煤化作用早期，孔隙主要受到压实作用和脱水作用的影响，煤中大孔和中孔的分形维数降低，随着变质程度的增加，孔隙的复杂程度逐渐增加［38］。在镜质组中［图7（c）］，D ct、D st和D mt随着镜质组的增加呈现增加的趋势。由于样品本身镜质组含量较高且在不断升高的同时，生气量变大，导致煤内部孔隙发生改变，由于煤体生气量增多，致使内部孔隙可能变形，结构变复杂，分形维数增加。通常镜质组与惰质组的变化量常常互补，从图7（d）中可以看出，不同分形维数的变化与镜质组相反。

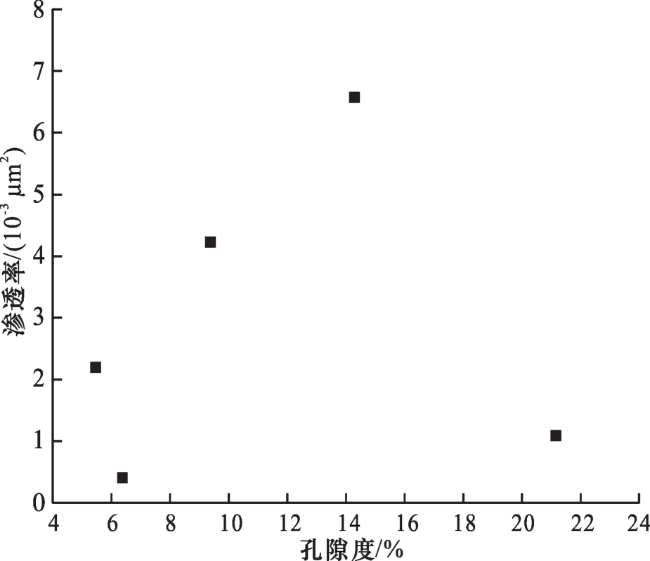
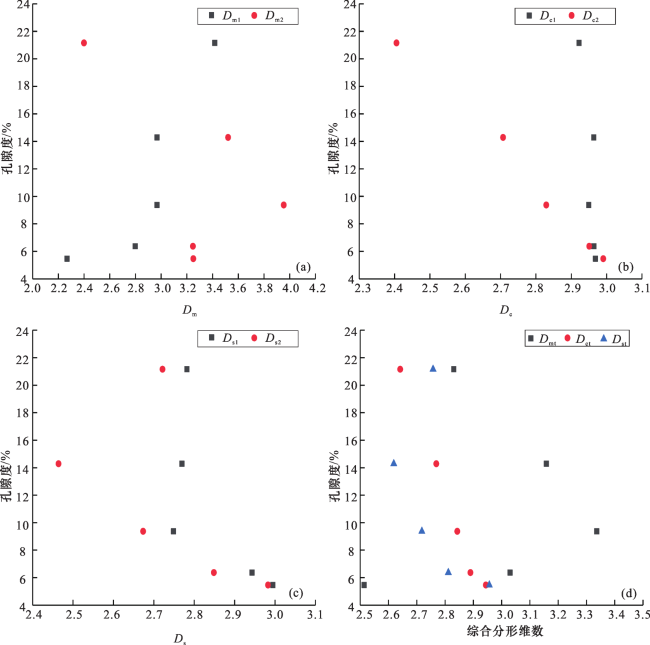
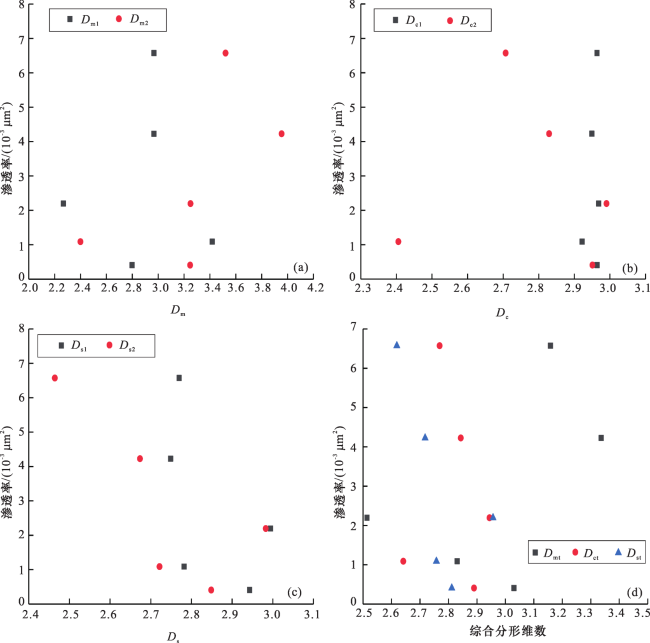
2.3.3　分形维数与孔隙度、渗透率的关系

煤中孔隙的发育程度是影响渗透的一个重要因素［39-40］，从图8中可以看出，孔隙度和渗透率的跨度偏大，整体呈现正相关。但是仅从孔隙度和渗透率的关系来分析并不全面，煤层中孔隙不同的连通性、延展性等也对渗透产生较大的影响，故进一步对煤中孔隙进行分析，由于孔隙作为渗流的通道，而大孔和中孔作为主要通道，故本文将引入不同模型大孔和中孔分形维数进行讨论。
图8 孔隙度和渗透率的关系

Fig.8 The relationship between porosity and permeability

通过建立综合分形维数与孔隙度和渗透率之间的关系［图9（d），图10（d）］，发现综合分形维数D t与样品的孔隙度和渗透率存在相对较好的线性关系，整体呈现负相关，表明分形维数越大，孔隙结构越复杂，样品的非均质性和物性越差。D 1和D 2相对应的孔是孔隙度的主要贡献者，其中不同模型中均体现出D 2与孔隙度和渗透率存在良好的负相关［图9（a）—图9（c），图10（a）—图10（c）］，在孔隙度方面毛细管综合模型相关程度最高，Sierpinski综合模型次之，Menger海绵综合模型最差，在渗透率方面Sierpinski综合模型相关程度最高，毛细管综合模型次之，Menger海绵综合模型最差；D 1与孔隙度和渗透率存在相关关系，且主要以Sierpinski综合模型的表征最为精准，能准确反映变化规律，毛细管综合模型呈垂直状态表明该模型未能准确反映该因素产生的影响，Menger海绵综合模型则表现为孔隙连通性的方面的考量较为忽略。
图9 分形维数与孔隙度的关系

（a） 孔隙度与D m分形维数； （b） 孔隙度与D c分形维数； （c） 孔隙度与D s分形维数； （d） 孔隙度与综合分形维数

Fig.9 The relationship between fractal dimension and porosity

图10 分形维数与渗透率的关系

（a） 渗透率与D m分形维数； （b） 渗透率与D c分形维数； （c） 渗透率与D s分形维数； （d） 渗透率与综合分形维数

Fig.10 The relationship between fractal dimension and permeability

2.4　分形模型评价

2.4.1　不同分形模型的分形维数对比

不同模型得出的分形维数之间存在相关关系，通过不同分形维数关系图的对比（图11）可以看出，D mt和D st之间总体呈现负相关，表明随着孔隙体积分形维数的增加，导致煤样表面的复杂程度和孔隙结构变复杂，当其扩大到一定程度时，致使内部孔隙结构的连通性变好，孔隙表面变平整，导致分形维数下降。D mt和D ct之间总体呈现增加的趋势，表明大尺度孔的分形维数的增加会使孔隙体积分形维数的增加，使孔隙结构稍变复杂。D st和D ct之间总体呈现正相关，表明孔隙表明的粗糙程度一定程度取决于大尺度孔隙的变化。
图11 分形维数之间的关系

（a） D s分形维数与D m分形维数； （b） D c分形维数与D m分形维数； （c） D s分形维数与D c分形维数

Fig.11 The relationship between fractal dimension

2.4.2　不同分形模型的适用性

通过建立不同的模型得出来的分形维数存在一定的表征差异，但是如果仅仅从彼此之间的线性关系以及相关性分析，只是从理论上得出成果，缺乏实际意义，故本文引入孔隙结构参数对不同分形模型的分形维数进行探讨，以期得出不同模型的适用性和对孔隙的定量表征。
通过分形维数和孔容的对比研究可以看出，Sierpinski综合模型和毛细管综合模型很好地表征煤储层孔隙的形态特征，Menger海绵综合模型由于整体跨度较大，故无法准确表征煤储层中孔隙的形态特征；考虑到分形维数与孔渗性的关系，不难发现，Sierpinski综合模型对孔隙孔渗性的结论合理、全面，毛细管综合模型对孔渗性的结论与之相似，但由于大孔未能表现出该规律，导致表现不明显。Menger海绵综合模型存在部分相反的规律，进一步表明Menger海绵综合模型和毛细管综合模型考虑参数有所局限；就煤层的组分而言，不同组分之间相互影响，不同组分含量会导致孔隙结构发生细微的变化进而影响分形维数，在本文实验中Sierpinski综合模型考虑了不同组分的影响，而毛细管综合模型欠缺了对水分的考虑，Menger海绵综合模型则对工业组分的反映不明显。但需要注意的是，本文实验由于受限于样本数量，故对于不同模型影响因素的分析可能出现不足，有待后续实验的进一步补充。

3 结论

（1）准噶尔盆地东南缘不同矿区主力煤层基于压汞实验和液氮实验分析，发现孔隙结构不尽相同，但总体连通性较好；孔径分布不一，总体以大孔和中孔较为分布；孔容主要由中孔和大孔贡献，过渡孔相对贡献较少，而比表面积主要由小于6 nm的小孔贡献。
（2）通过建立不同模型表征煤层孔隙的复杂程度，可以看出不同模型均呈现分段的特征，总体表现为区内煤层储层中大孔结构较中孔更复杂，渗流孔的分形特征最为明显。
（3）通过综合分形维数的建立，对煤岩的物性、孔渗等方面进行分析，基于水分和灰分不同含量对煤中孔隙复杂程度的不同作用、镜质组和惰质组生气量的变化对孔隙结构的影响以及孔隙度和渗透率与分形维数的关系，综合评判了不同模型的适用性。结果表明Sierpinski模型对本文实验挑选的影响因素表征效果最好，其适用性和优选性最高。

References

Publishing order | Descend order by publishing year | Descend order by cited within
1
MEYERS R A. Coal Structure［M］. New York：Academic Press，1982.

2
RODRIGUES C F，LENOS M J. The measurement of coal porosity with different gases［J］.International Journal of Coal Geology，2002，48（3-4）：245-281.

3
王凯，乔鹏，王壮森，等. 基于二氧化碳和液氮吸附、高压压汞和低场核磁共振的煤岩多尺度孔径表征［J］. 中国矿业，2017，26（4）：146-152.

WANG K，QIAO P，WANG Z S，et al. Multiple scale pore size characterization of coal based on carbon dioxide and liquid nitrogen adsorption，high-pressure mercury intrusion and low field nuclear magnetic resonance［J］. China Mining Magazine，2017，26（4）：146-152.

4
傅雪海，秦勇，张万红，等. 基于煤层气运移的煤孔隙分形分类及自然分类研究［J］. 科学通报，2005，50（S1）：51-55.

FU X H，QIN Y，ZHANG W H，et al. Research on coal pore fractal classification and natural classification based on coalbed methane migration［J］.Chinese Science Bulletin，2005，50（S1）：51-55.

5
秦勇，徐志伟，张井. 高煤级煤孔径结构的自然分类及其应用［J］. 煤炭学报，1995，20（3）：266-271.

QIN Y，XU Z W，ZHANG J. Natural classification of the high-rank coal pore structure and its application［J］. Journal of China Coal Society，1995，20（3）：266-271.

6
王文峰，徐磊，傅雪海. 应用分形理论研究煤孔隙结构［J］. 中国煤炭地质，2002，14（2）：27-28，34.

WANG W F，XU L，FU X H. Study on pore texture of coal with fractal theory［J］. Coal Geology of China，2002，14（2）：27-28，34.

7
傅雪海，秦勇，薛秀谦，等. 煤储层孔、裂隙系统分形研究［J］. 中国矿业大学学报，2001，30（3）：11-14.

FU X H，QIN Y，XUE X Q，et al. Research on fractals of pore and fracture-structure of coal reservoirs［J］. Journal of China University of Mining & Technology，2001，30（3）：11-14.

8
MANDELBORT B B. Stochastic models for the earth’s relief，the shape and the fractal dimension of the coastlines，and the number-area rule for islands［J］. Peoceedings of the National Academy of Sciences of the USA，1975，72：3825-3828.

9
PEREZ G，CHOPRA A K. Evaluation of Fractal Models to Describe Reservoir Heterogeneity and Performance［C］. America：SPE22694-PA，1997：65-72.

10
PFEIFER P，AVNIR D. Chemistry in noninteger dimensions between two and three.I Fractal theory of heterogeneous surfaces［J］. The Journal of Chemical Physics，1983，79（7）：3558-3565.

11
CAI Y D，LIU D M，YAO Y B，et al. Fractal characteristics of coal pores based on classic geometry and thermodynamics models［J］. Acta Geologica Sinica，2011， 85（5）：1150-1162.

12
YAO Y B，LIU D M，TANG D Z，et al. Fractal characterization of adsorption-pores of coals from North China： An inbestigation on CH4 adsorption capacity of coals［J］. International Journal of Coal Geology，2008，73（11）：27-42.

13
YAO Y B，LIU D M，TANG D Z，et al. Fractal characterization of seepage-pores of coals from China：An investigation on permeability of coals［J］. Computers & Geosciences，2009，35（6）：1159-1166.

14
高北斗，王海超，田继军，等. 准南煤田硫磺沟矿区向斜—承压式煤层气富集模式［J］. 现代地质，2020，34（2）：281-288.

GAO B D，WANG H C，TIAN J J，et al. Syncline-confined-water model of coalbed methane enrichment area in Liuhuanggou mining area，southern Junggar Coalfield［J］. Geoscience，2020，34（2）：281-288.

15
孙景龙，郎海亮，张伟，等. 新疆准南某井田煤层气资源评价及有利区优选［J］. 中国煤层气，2018，15（3）：7-11.

SUN J L，LANG H L，ZHANG W，et al. CBM resource evaluation and favorable area analysis in a well field of southern Junggar in Xinjiang Province［J］.China Coalbed Methane，2018，15（3）：7-11.

16
张奥博，汤达祯，唐淑玲，等. 准噶尔盆地南缘沉积控制下含煤层气系统构成研究［J］. 煤炭科学技术，2019，47（1）：255-264.

ZHANG A B，TANG D Z，TANG S L，et al. Study on composition of coalbed methane system under sedimentary control in southern margin of Junggar Basin［J］. Coal Science and Te-chnology，2019，47（1）：255-264.

17
龙华山，王绪龙，向才富，等. 准噶尔盆地南缘侏罗系烃源岩评价［J］. 现代地质，2013，27（5）：1070-1080.

LONG H S，WANG X L，XIANG C F，et al. Evaluation on Jurassic hydrocarbon source rock developed in southern margin of Junggar Basin［J］. Geoscience，2013，27（5）：1070-1080.

18
OU C H，LI C C，ZHI D M，et al. Coupling accumulation model with gas-bearing fertures to evaluate low-rank coalbed methane resource potential in the southern Junggar Basin，China［J］. AAPG Bulletin，2018，102（1）：153-174.

19
LI C C，LIU D M，CAI Y D，et al. The microfissure characteristics and mineral control analysis of coal reservoir in the southern margin of the Junggar Basin，Xinjiang［J］. Coal Science and Technology，2015，43（12）：144-151.

20
马如英，王猛，阿斯亚·巴克，等. 准东南低阶煤覆压孔渗试验研究［J］. 中国矿业大学学报，2020，49（6）：1182-1192.

MA R Y，WANG M，ASIYA B K，et al. Experimental study of overburden pore porosity and permeability of low-rank coal reservoirs in southeastern Junggar［J］. Journal of China University of Mining & Technology， 2020，49（6）：1182-1192.

21
许婷，伏海蛟，马英哲，等. 准噶尔盆地东南缘煤层气勘探目标优选［J］. 特种油气藏，2017，24（2）：18-23.

XU T，FU H J，MA Y Z，et al. Selection of CBM exploration targets in southeastern margin of Junggar Basin［J］. Special Oil and Gas Reserviors，2017，24（2）：18-23.

22
李旭. 不同变质程度煤孔隙体积分形研究［J］. 煤炭技术，2020，39（7）：88-90.

LI X. Fractal study on pore volume of coals with different metamorphic degrees［J］. Coal Technology，2020，39（7）：88-90.

23
许耀波，朱玉双. 高阶煤的孔隙结构特征及其对煤层气解吸的影响［J］. 天然气地球科学，2020，31（1）：84-92.

XU Y B，ZHU Y S. Pore structure characteristics of high rank coal and its effect on CBM desorption［J］. Natural Gas Geoscience，2020，31（1）：84-92.

24
朱炎铭，王阳，陈尚斌，等. 页岩储层孔隙结构多尺度定性-定量综合表征：以上扬子海相龙马溪组为例［J］. 地学前缘，2016，23（1）：154-163.

ZHU Y M，WANG Y，CHEN S B，et al. Qualitative-quantitative multiscale characterization of pore structures in shale reservoirs：A case study of Longmaxi Formation in the Upper Yangtze area［J］. Earth Science Frontiers，2016，23（1）：154-163.

25
刘世明，唐书恒，霍婷，等. 柴达木盆地东缘上石炭统泥页岩孔隙结构及分形特征［J］. 天然气地球科学，2020，31（8）：1069-1081.

LIU S M，TANG S H，HUO T，et al. Pore structure and fractal characteristics of the Upper Carboniferous shale，eastern Qaidam Basin［J］. Natural Gas Geoscience，2020，31（8）：1069-1081.

26
MANDELBROT B B，WHEELER J A. The fractal geometry of nature［J］. Journal of the Royal Statistical Society，1982，147（4）：468.

27
杨宇，孙晗森，彭小东，等. 煤层气储层孔隙结构分形特征定量研究［J］. 特种油气藏，2013，20（1）：31-33，88，152.

YANG Y，SUN H S，PENG X D，et al. Quantitative study on fractal characteristics of the structure of CBM reservoir［J］. Special Oil and Gas Reserviors，2013，20（1）：31-33，88，152.

28
胡宝林，张志龙，车遥，等. 鄂尔多斯盆地煤储层孔隙分形特征研究［J］. 淮南工业学院学报，2002，22（4）：1-4.

HU B L，ZHANG Z L，CHE Y，et al. Research on characteristics of fractures of coal reservoirs porosity in the Ordos Basin［J］. Journal of Huainan Institute of Technology，2002，22（4）：1-4.

29
陈向军，赵伞，司朝霞，等.不同变质程度煤孔隙结构分形特征对瓦斯吸附性影响［J］.煤炭科学技术，2020，48（2）：118-124.

CHEN X J，ZHAO S，SI C X，et al. Fractal characteristics of pore structure of coal with different metamorphic degrees and its effect on gas adsorption characteristics［J］. Coal Science and Technology，2020，48（2）：118-124.

30
李希建，薛海腾，陈刘瑜，等.贵州地区突出煤层微孔结构及对瓦斯流动特性的影响［J］.煤炭科学技术，2020，48（10）：67-74.

LI X J，XU H T，CHEN L Y，et al. Micropore structure of outburst coal in Guizhou Area and its influence on gas flow［J］. Coal Science and Technology，2020，48（10）：67-74.

31
卜婧婷. 新疆矿区中低阶煤全孔径孔隙结构特征的实验研究［D］. 西安：西安科技大学，2019.

BU J T. Experimental Study of Pore Structure Characteristics of Full-aperture Section of Middle and Low Rank Coal in Xinjiang Mining Area［D］. Xi’an：Xi’an University of Science and Technology，2019.

32
宋昱，姜波，李凤丽，等. 低—中煤级构造煤纳米孔分形模型适用性及分形特征［J］. 地球科学，2018，43（5）：1611-1622.

SONG Y，JIANG B，LI F L，et al. Applicability of fractal models and nanopores’ fractal characteristics for low-middle rank tectonic deformed coals［J］. Earth Science，2018，43（5）：1611-1622.

33
王小垚，曾联波，周三栋，等. 低阶煤储层微观孔隙结构的分形模型评价［J］. 天然气地球科学，2018，29（2）：277-288.

WANG X Y，ZENG L B，ZHOU S D，et al. Assessment of micro-pore structure fractal model evaluation of low-rank coal reservoirs［J］. Natural Gas Geoscience，2018，29（2）：277-288.

34
李子文. 低阶煤的微观结构特征及其对瓦斯吸附解吸的控制机理研究［D］. 北京：中国矿业大学，2015.

LI Z W. Study on Microstructure Characteristics of Low Rank Coal and Its Control Mechanism on Gas Adsorption/Desorption［D］.Beijing：China University of Mining and Technology，2015.

35
王飞，邢好运，李万春，等. 中低阶煤的孔隙结构演化特征［J］. 西安科技大学学报，2020，40（3）：384-392.

WANG F，XING H Y，LI W C，et al.Evolution characteristics of pore structure in medium and low rank coal［J］.Journal of Xi’an University of Science and Technology，2020，40（3）：384-392.

36
张松航，唐书恒，汤达祯，等. 鄂尔多斯盆地东缘煤储层渗流孔隙分形特征［J］. 中国矿业大学学报，2009，38（5）：713-718.

ZHANG S H，TANG S H，TANG D Z，et al. Fractal characteristics of coal reservoir seepage pore，east margin of Ordos Basin［J］. Journal of China University of Mining & Technology，2009，38（5）：713-718.

37
王有智. 珲春盆地八连城矿区煤岩孔隙分形特征［J］. 西南石油大学学报：自然科学版， 2020， 42（1）： 57-68.

WANG Y Z. Fractal characteristics of coal rock pores in the Baliancheng Mining area，Hunchun Basin［J］. Journal of Southwest Petroleum University：Science & Technology Edition，2020，42（1）：57-68.

38
刘顺喜，吴财芳. 比德-三塘盆地煤储层不同尺度孔隙分形特征研究［J］. 煤炭科学技术，2016，44（2）：33-38，67.

LIU S X，WU C F. Study on fractal characteristics of different scales pore coal reservoir in Bide-Santang Basin［J］. Coal Science and Technology，2016，44（2）：33-38，67.

39
杨师宇，姚艳斌，魏韧，等. 乌鲁木齐河东矿区煤储层渗流孔孔隙分形特征研究［J］. 煤炭科学技术，2020，48（8）：175-183.

YANG S Y，YAO Y B，WEI R，et al. Fractal characteristics of seepage pore in coal reservoirs in Hedong mining area，Urumqi［J］. Coal Science and Technology，2020，48（8）：175-183.

40
李磊. 页岩孔渗特性的分维特征及储层预测意义［J］. 煤炭技术，2020，39（7）：65-68.

LI L. Fractal dimension features of porosity and permeability of shale and significance of reservoir forecast［J］. Coal Technology，2020，39（7）：65-68.

Options
Outlines

/

〈 〉

陇ICP备2021001824号-7　 甘公网安备 62010202000678号
Copyright © Natural Gas Geoscience, All Rights Reserved.
Tel: (0931)8277790　
E-mail：geogas@lzb.ac.cn
Total visitors:　 Visitors of today: 　 Now online:
Powered by Beijing Magtech Co. Ltd,.