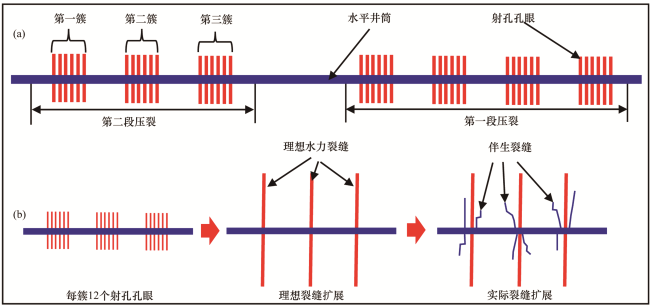
0 引言
1 数学模型
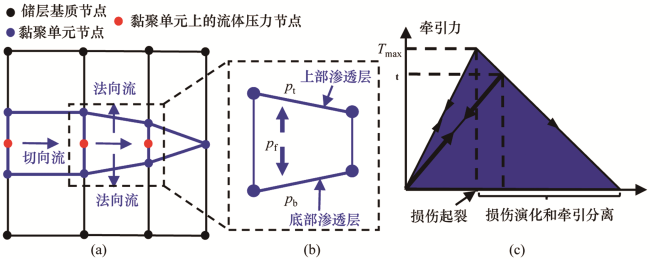
1.1 裂缝扩展模型
1.2 牵引分离定律
1.3 流体流动与地质力学耦合模型
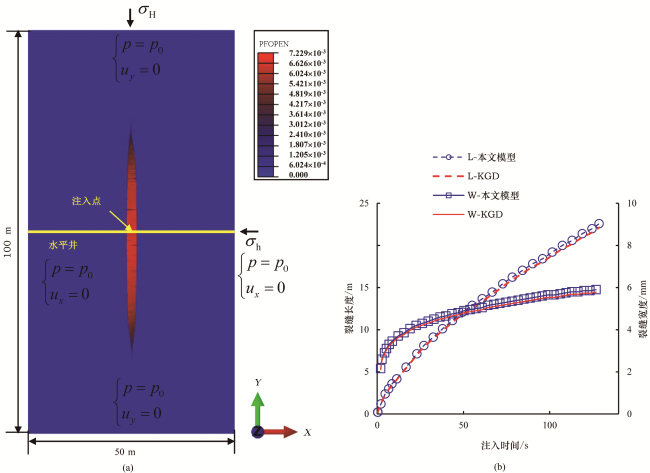
2 模型验证
图3 KGD解析解与本文模型结果的对比Fig.3 Comparison between the KGD analytical solution and the model results in this paper |
表1 模型中主要的输入参数Table 1 Main input parameters in the model |
| 输入参数 | 值 |
|---|---|
| 孔隙度 | 0.1 |
| 初始孔隙压力/MPa | 10 |
| 基质抗张强度/MPa | 5 |
| 基质抗剪切强度/MPa | 20 |
| 岩石的拉伸临界断裂能/(J/m2) | 100 |
| 岩石的剪切临界断裂能/(J/m2) | 4 500 |
| 弹性模量/GPa | 10 |
| 泊松比 | 0.25 |
| 流体黏度/(mPa·s) | 1 |
| 流体比重/(KN/m3) | 9.8 |
| 滤失系数/[(m³/s)·Pa] | 1×10-14 |
| 摩擦系数 | 0.615 |
3 结果讨论与分析
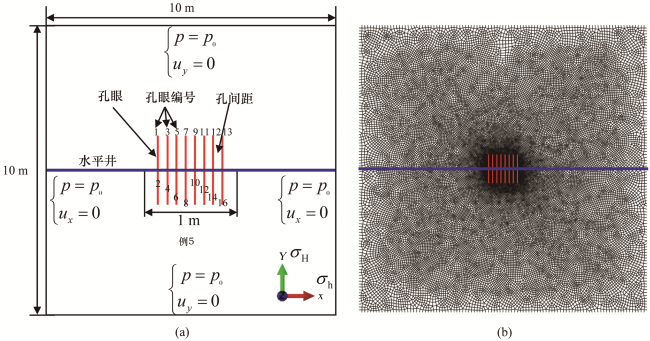
3.1 模型建立
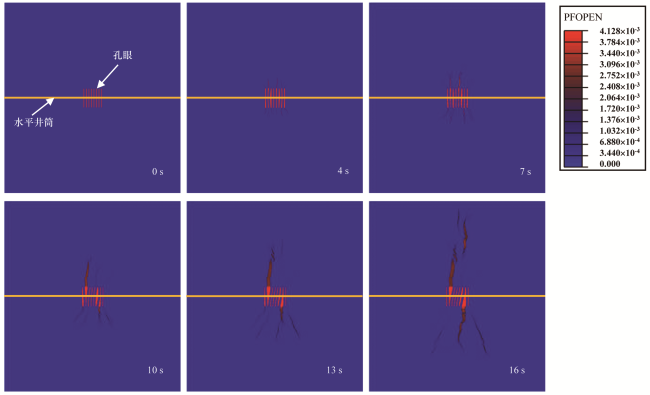
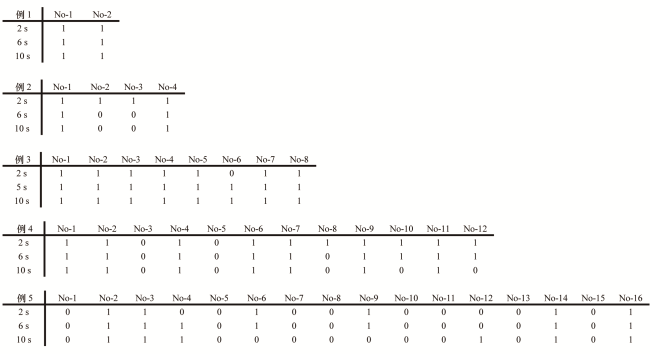
3.2 射孔密度对裂缝起裂的影响
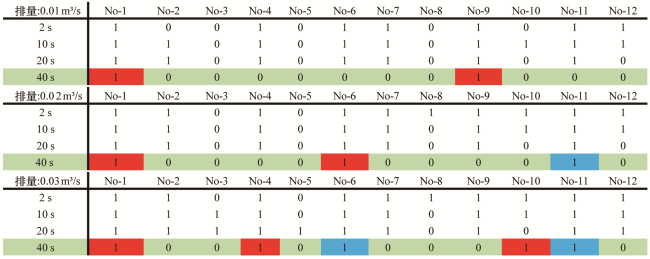
图7 孔眼在不同注入时间的起裂与闭合情况Fig.7 Crack initiation and closure of each hole at different injection times |
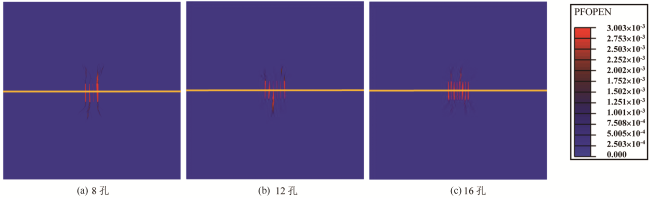
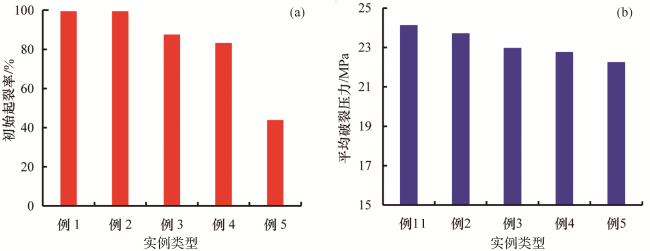
3.3 射孔密度对裂缝扩展的影响
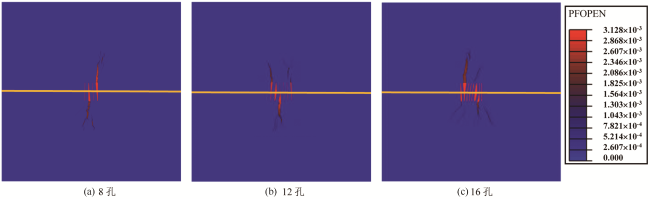
图9 在10 s时不同射孔密度对应裂缝扩展形态的比较Fig.9 Comparison of fracture propagation morphology with different perforation densities at 10s |
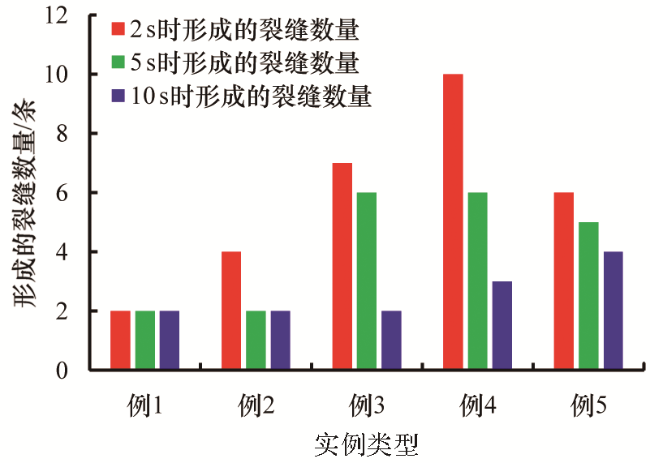
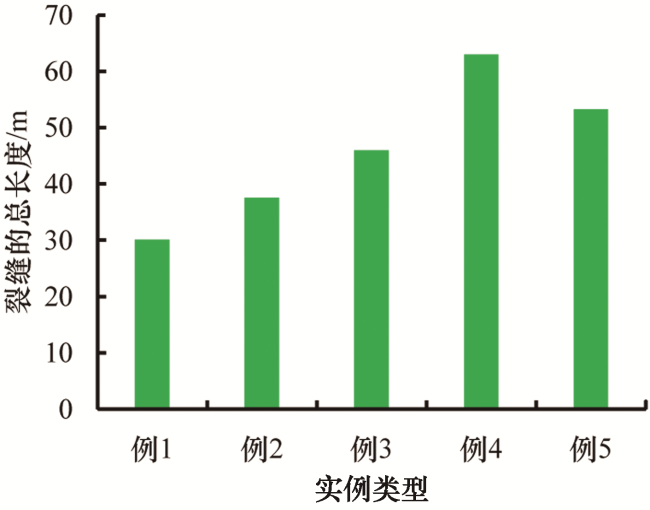
图10 5个实例在不同时刻的裂缝数量(基于孔眼底部的裂缝扩展情况进行统计)Fig.10 The number of fractures in five examples at different times (based on the fracture propagation at the bottom of the hole) |
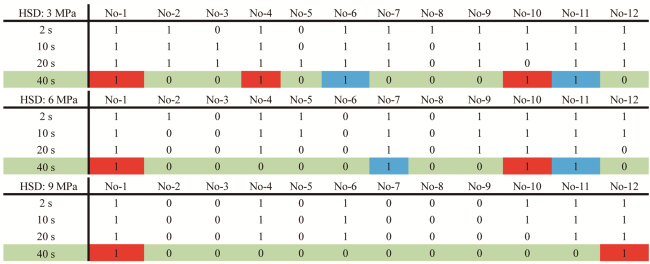
3.4 排量、黏度、应力差对多孔眼裂缝起裂与扩展的影响
图12 排量对多孔眼裂缝起裂与扩展的影响Fig.12 Influence of displacement on the initiation and propagation of multi-hole cracks |
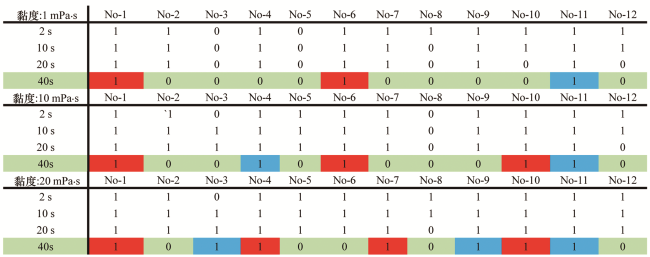
图13 黏度对多孔眼裂缝起裂与扩展的影响Fig.13 Influence of viscosity on the initiation and propagation of multi-hole cracks |



 甘公网安备 62010202000678号
甘公网安备 62010202000678号