0 引言
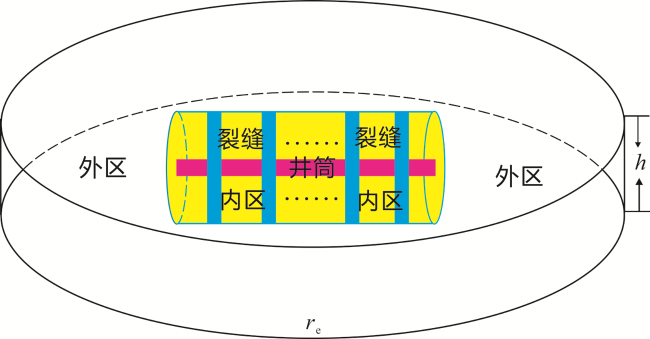
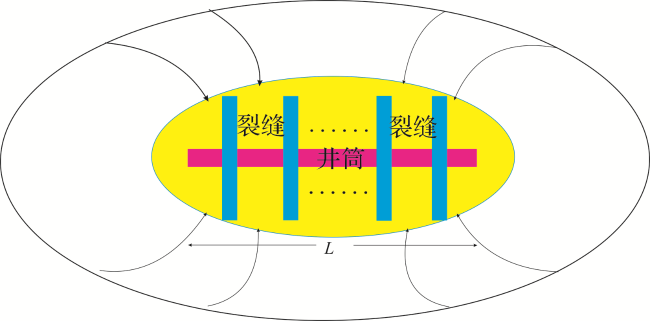
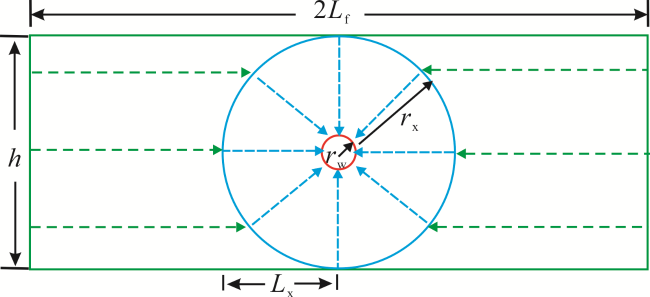
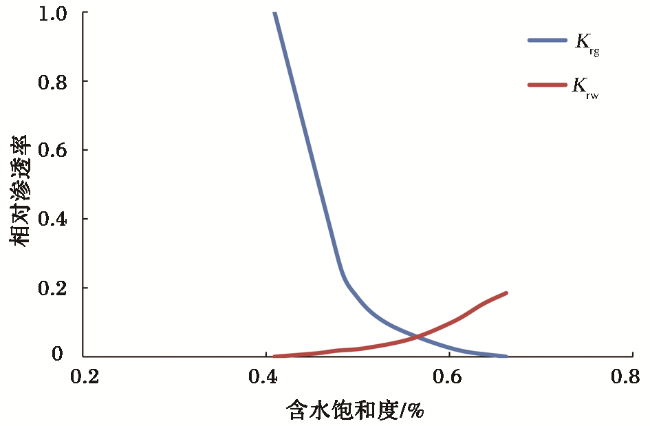
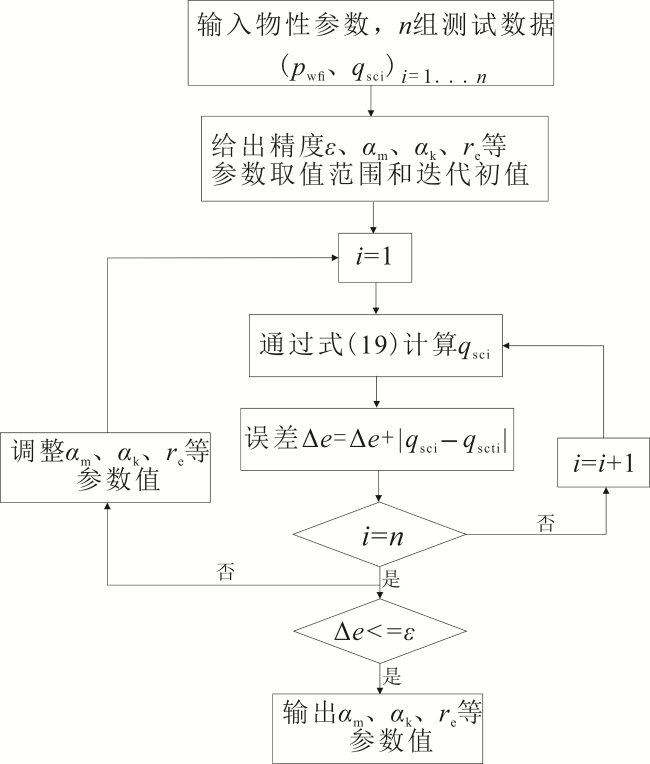
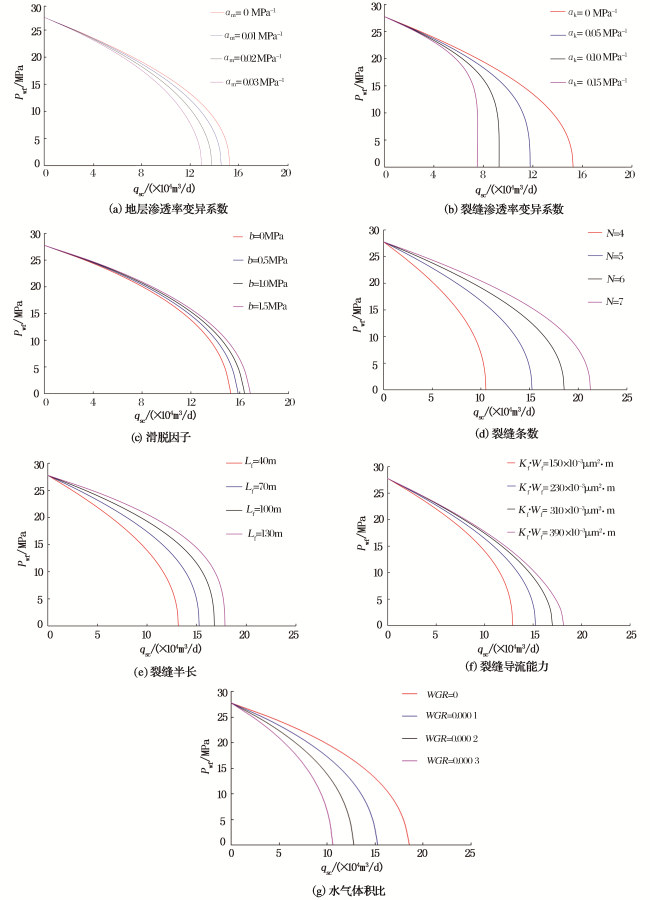
低渗气藏物性差，同时受到非达西效应的影响，常规气井无法实现工业化生产，而水力压裂是一种使用范围广且有效的增产技术。此外，对于天然水体活跃的气藏，渗流规律会伴随着开发过程中边底水的锥进而变得更加复杂，那么常规产能预测模型将不再适用。目前，关于压裂水平井气水两相渗流规律及产能方面的研究，一部分学者研究了低渗情况下压裂水平井的渗流规律，但未同时考虑非达西效应和产水的影响[1,2,3,4,5,6]；还有学者建立气水两相流体的拟压力函数来分析气井产能的变化，但仅适用于一般的直井、水平井或压裂直井[7,8,9,10]；另外一些学者利用保角变换等常规方法研究气井的产能，虽能在一定程度上描述气井的渗流规律，但这样的求解思路过于陈旧[11,12,13,14]；以上研究都或多或少存在一些不完善的地方。笔者充分考虑地层中和裂缝内气水两相流体所表现出的不同渗流规律，分区分阶段进行流动阶段的划分，并创新性地引入椭圆坐标系下标度因子的方法，建立椭圆坐标系与直角坐标系的关系。在此基础上，充分考虑近井筒内高速非达西、地层及裂缝内应力敏感、地层低压下滑脱效应的影响，建立新的气水两相拟压力函数，并运用当量井径原理和势的叠加原理，推导出低渗气藏压裂水平井气水两相产能模型。通过实例验证，模型可靠且适用性强，另外根据敏感性因素分析也坚定了做好水平气井压裂设计以及防水治水的必要性。
1 物理模型
某低渗透强边水气藏顶底封闭，储层有效厚度为h，一口水平气井位于其中央，泄气半径为r e（图1）。水力压裂后形成若干条裂缝，裂缝等长且分布均匀，其裂缝高度与储层等厚；裂缝内存在压降，为有限导流，井筒内不考虑压降，为无限导流；整个流动过程为气水两相，考虑稳态渗流，无化学反应发生；忽略重力、毛管力的影响。
通过对气水两相渗流规律分析，将流体在地层内流动区域划分为外区和内区：外区为地层内发生的基质与裂缝间的椭圆渗流，内区为裂缝内发生的线性与径向流动。
2 压裂水平井产能预测模型
2.1 外区（地层）流动
水力压裂后，新产生的裂缝会影响流体在地层中的渗流规律，研究认为会生成以供给边缘为外边界，水平井筒及裂缝控制区边缘为内边界的椭圆流动（图2）。
通过直角坐标系与椭圆坐标系的几何关系，其表达式如下：
其中： 。
式（1）中：x、y为直角坐标，无量纲；η、ξ为椭圆坐标，无量纲；a、b分别为椭圆长半轴长、短半轴长,m；L f为裂缝半长，m。
水相在地层内渗流数学模型可表示为：
式（2）—式（3）中： 为压力梯度，MPa/m； 为哈密尔顿（Hamilton）算符；μ g为气相黏度，mPa·s；K为地层绝对渗透率，×10-3μm2；K rg为气相相对渗透率，无量纲；K rw为水相相对渗透率，无量纲；μ w为水相黏度，mPa·s；v g为气相在地层内渗流速度，m/d；v w为水相在地层内渗流速度，m/d；K m0为原始地层压力下地层渗透率，×10-3μm2；b为气体滑脱因子，MPa； 为地层流动区域的平均压力，MPa；α m为地层应力敏感系数，MPa-1；p i为原始地层压力，MPa。
根据椭圆坐标系下哈密尔顿算符 的相关定义，其可以表示为：
其中： 。
式（4）中：h ξ为椭圆坐标ξ的标度因子，m；h η为椭圆坐标η的标度因子，m。
气体的渗流速度可表示为单位渗流面积下的气体流量：
利用气体在地下体积与地面体积的转换关系，同时对式（5）进行积分，可得：
根据微分思想，椭圆的微元弧长段可表示为：
将式（7）带入式（6）中，可得：
式（5）—式（8）中：q g为气体流量（地下），m3/d；A为渗流面积，m2；ρ gsc为地面标准状况下气相密度，g/cm3；q gsc1为标准状况下气相体积流量，m3/d；ρ g为地层条件下的气相密度，g/cm3；h为储层有效厚度，m。
由式（8）可得气相渗流速度方程为：
同理，水相在地层内渗流速度方程为：
式（10）中：ρ w为地层条件下的气相密度，g/cm3；q w1为标准状况下水相体积流量，m3/d。
将式（4）、式（9）、式（10）代入式（2）、式（3）中，进行变量分离后化简相加可得：
定义WGR为水相和气相的体积流量比值，那么其质量流量可表示为：
将地层内两相拟压力函数 引入式（11）并积分，其中ξ从ξ f到ξ e，p从p f到p e，同时代入式（12），可得到地层中考虑产水影响的流动方程：
根据椭圆供给边界及内边界的对应关系， ， 。
式（13）中：p f为裂缝尖端压力，MPa；ξ e为供给边界坐标，无量纲；ξ f为内边界坐标，无量纲。
2.2 内区（裂缝）流动
将裂缝等效为一个长方体（长为L f,宽为W f,高为h），由于裂缝内渗透率高且近井筒区域压降较大，流体在裂缝中会形成2个流动阶段（图3）：①裂缝尖端到近井筒区域的线性流：该流动区类似于带状地层，其供给边缘为裂缝边缘L f，排液道为L x。②近井筒区域的径向流：该流动区类似于圆形地层，其供给外边界为r x，供给内边界为r w。
与流体在地层内渗流规律同理，流体在裂缝中会受到更为强烈的应力敏感效应，同时气相在高速流动时会产生高速非达西效应[17]，考虑其影响，气相的渗流数学模型可由以下基本方程组成：
水相不受高速非达西效应的影响，其他参考气相运动方程的推导，水相在裂缝内渗流数学模型可表示为：
式（14）—式（15）中：K f为裂缝绝对渗透率，×10-3μm2；β g为裂缝内气相紊流系数，m-1；ρ g为气体密度，g/cm3；v gl为气相在线性流动区的流速，m/d；q gsc2为标准状况下气相在线性流动区的体积流量，m3/d；q w2为标准状况下水相在线性流动区的体积流量，m3/d；W f为裂缝宽度，m；v gx为气相在径向流动区的流速，m/d；q gsc3为标准状况下气相在径向流动区的体积流量，m3/d；q w3为标准状况下水相在径向流动区的体积流量，m3/d；K f0为裂缝原始压力下的渗透率，×10-3μm2；α f为裂缝应力敏感系数，MPa-1。
引入裂缝区域内两相拟压力函数 ，并联立式（14）、式（15），对式子进行积分化简后可得裂缝中考虑产水影响的流动方程：
其中：L x=r x=h/2。
式（16）中：p wf为井底流压，MPa；L x为线性流动区排液道，m；r x为径向流动区外边界，m；r w为井筒半径，m； 为线性流动区平均压力，MPa； 为径向流动区平均压力，MPa。
2.3 压裂水平井产能方程的建立及求解
2.3.1 压裂水平井产能方程的建立
基于对流体在地层中和裂缝内渗流规律的分析，利用水电相似原理，可知不同流动区气相的体积流量相等，即q gsc=q gsc1=q gsc2=q gsc3，带入式（13）、式（16）可得压裂水平井在考虑有限导流情况下裂缝的产能方程为：
式（17）为多元非齐次方程组，且这仅为单条裂缝产能公式，如存在多条裂缝时此方程组求解难度将会呈指数级增加，因此为实现简化快速计算的目的，这里引入当量井径将裂缝等效为普通直井的方法进行计算，以将复杂的多元非齐次方程进行降次。根据达西渗流理论，考虑应力敏感、滑脱效应的普通直井产能方程可表示为：
对式（18）与式（17）而言，假定产量q gsc相等，通过非线性方程组的迭代计算可求得井筒半径，此井筒半径即为当量井径。
将多条裂缝等效为多口直井，考虑其互相干扰，运用压降叠加原理，可得到考虑裂缝干扰下的压裂水平井产能方程组：
2.3.2 压裂水平井产能方程的求解
对于本文推导的压裂水平井产能方程，主要涉及到气水两相拟压力函数以及线性方程组的求解。
在稳定渗流条件下，根据气水两相运动方程可得：
式（20）中：B g为气相体积系数，无量纲；B w为水相体积系数，无量纲。
（1）气水两相拟压力函数：压力变化对μ w、B w影响较小，可将其视为常数；μ g、B g可表示为压力的关系式，其中μ g可根据Lee等公式[18]进行计算，B g=ZTpsc/T sc p；K rg、K rw可根据相渗曲线确定含水饱和度S w与K rg/K rw的函数关系，同时结合式（20）中p与K rg/K rw的关系，可得到p与S w的关系，进一步得到p分别与K rg、K rw的关系。
（2）线性方程组求解：在矿场计算中，首先确定好裂缝条数，根据式（19）建立确定的线性方程组。由于将井筒考虑为无限导流，不存在压降，因此各裂缝与井筒交接处流压相等，即p wf1=p wf2=…=p wf。在此基础上再利用数值解法（高斯—若当消元法）或迭代解法（高斯—塞德尔迭代法）进行求解，得到各条裂缝的产量q gsc1，q gsc2，…，q gsc n ，压裂水平井总产量即为各条裂缝的产量之和。
3 实例分析
3.1 产能计算
表1 气藏基本参数Table 1 Basic parameter table of gas reservoir |
| 井名 | 原始地层压力(p i)/MPa | 供给边界压力(p e)/MPa | 地层温度(T)/K | 地层原始渗透率(K m0)/(×10-3μm2) |
|---|---|---|---|---|
| 气藏有效厚度(h)/m | 地层渗透率变异系数(α m)/MPa-1 | 滑脱因子(b)/MPa | 泄气半径(r e)/m | |
| A1 | 29.3 | 28.2 | 367.4 | 0.5 |
| 15.4 | 0.01 | 0.4 | 420 | |
| A2 | 28.7 | 27.8 | 366.3 | 0.09 |
| 16.7 | 0.01 | 0.4 | 395 |
表2 气井压裂参数Table 2 Fracturing parameter table of gas well |
| 井名 | 裂缝半长(L f)/m | 裂缝导流能力(K fo·W f)/(×10-3μm2·m) | 裂缝条数 | 井筒半径(r w)/m | 裂缝渗透率变异系数(α k)/MPa-1 |
|---|---|---|---|---|---|
| A1 | 70.3 | 229.4 | 5 | 0.107 9 | 0.08 |
| A2 | 61.6 | 213.2 | 7 | 0.107 9 | 0.08 |
目前A1井水气体积流量比为0.000 1m3/m3，A2井水气体积流量比为0.000 2m3/m3，地层水密度为1.0g/cm3，地层水黏度为0.8mPa·s。由气水相渗实验可获得气水两相相渗曲线，如图4所示。
根据以上的基础参数，利用式（19）进行计算，可得A1井与A2井的无阻流量，如表3所示。
表3 产能评价结果Table 3 Evaluation result table of productivity |
| 井名 | 压裂气井无阻流量（q AOF）/(×104m3/d) | |
|---|---|---|
| 本文计算公式 | 修正等时试井 | |
| A1 | 15.25 | 16.08 |
| A2 | 22.46 | 23.97 |
从表3中数据可以看出，本文公式与修正等时试井计算无阻流量相差较小，相对误差分别为5.4%和6.7%，均小于8.0%，说明本文建立的产能方程能很好地满足现场的实际应用。
另外考虑到本文中需要使用的部分参数难以获取，如地层渗透率变异系数α m、裂缝渗透率变异系数α k、泄气半径r e等，本文提出利用产能测试数据进行自动拟合的算法。利用多组实际产能测试数据（包括井底流压p wf、产气量q sc）拟合α m、α k、r e等，计算流程如图5所示。
3.2 敏感性分析
不同的地层、裂缝、流体参数对气井产能的影响程度不同，因此有必要分析各因素的敏感性，以期指导压裂水平井对气藏的合理开发。基于之前的认识，接下来分析地层和裂缝应力敏感性、气体滑脱效应、不同的裂缝参数以及水气体积比对气井产能的影响，如图6所示(见下页)。
从图6（a）、图6（b）来看，渗透率变异系数与气井产能呈负相关且裂缝应力敏感对气井产能的影响更为显著，主要原因为流体在裂缝内的渗流能力更强，因此裂缝物性的变化对流体的渗流影响更大。如图6（c）所示，滑脱因子越大，气井无阻流量越高，但整体来看影响并不是太大，原因为滑脱效应仅是气固两相边界层上的反应，对整个流体的渗流影响较小。图6（d）—图6（f）为裂缝参数的影响，可看到裂缝数量、裂缝半长、裂缝导流能力的增加对气井产能都有正面效果，但它们都存在一个最优值，主要原因为裂缝间距、流体流线的变化导致裂缝间产生干扰、渗流阻力增大，正面和负面的效果有一定的抵消作用。低渗气藏中气井产量相对较低，当气井产水后，气井无法很好地携液，那么井底势必会因积液而产生趟井风险。如图6（g）所示，水气体积流量比对气井产能影响十分显著，随着水气体积比的增加，水相堵塞孔道，造成气相渗透率迅速降低，地层能量消耗增加，气井无阻流量降低。
4 结论
（1）在充分考虑气水两相在地层和裂缝中渗流规律的基础上，分区分阶段进行流动阶段的划分，打破了传统的产能公式推导方法，创新性地引入椭圆坐标系下的标度因子和气水两相拟压力，运用当量井径理论和多井干扰下势的叠加原理，推导了应力敏感效应、滑脱效应、高速非达西效应影响下的低渗气藏压裂水平井气水两相产能模型，并通过实例验证了其可靠性。
（2）通过对非达西效应、裂缝参数、水气体积比等的分析，认识到非达西效应中裂缝的应力敏感性对产能影响较大，因此在气田投入开发前应加强对裂缝应力敏感的研究，避免对产能认识的偏差；随着裂缝参数值的增加，其对产能的影响幅度逐渐变缓，因此在压裂施工前应做好压裂设计，以保证气井产能及经济性的最大化；产水对气井产能的影响较大，需随时关注气井的生产动态，在做好防水控水的同时也应加强治水措施的研究。
甘公网安备 62010202000678号
