0 引言
1 F气田地质概况
2 孔隙度计算方法原理
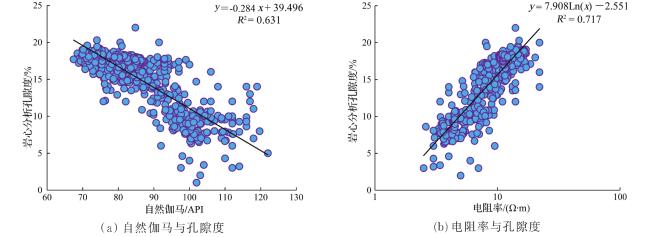
2.1 基于数理统计的孔隙度计算方法
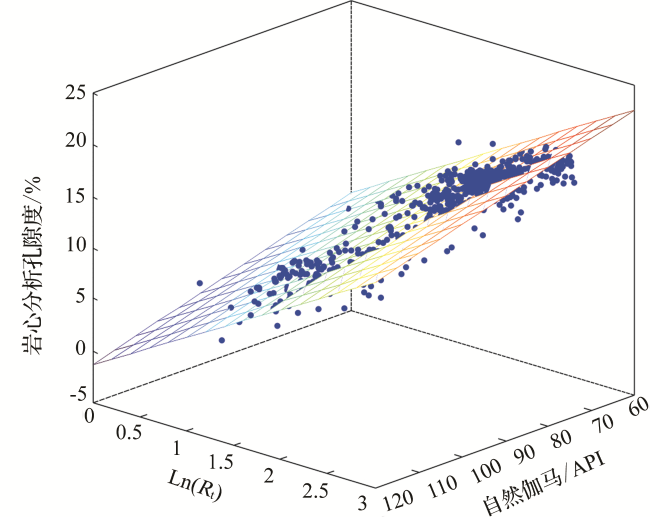
2.2 基于理论模型推导的孔隙度计算新方法
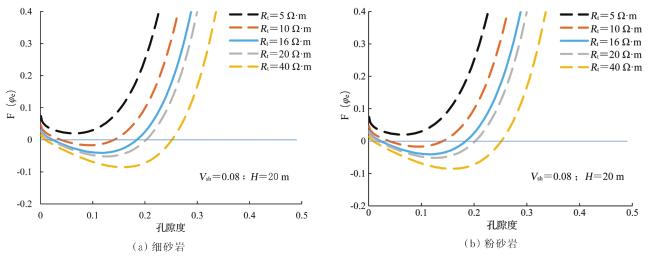
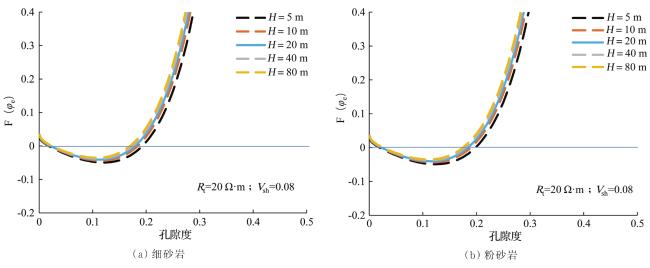
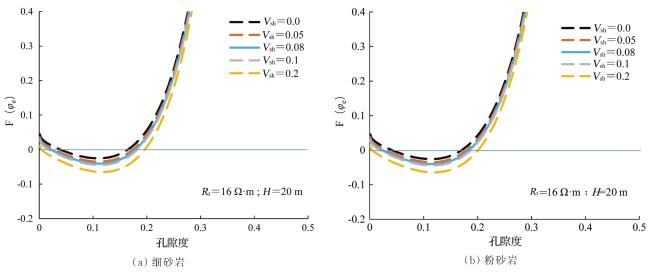
2.2.1 储层电阻率与孔隙度、含水饱和度和泥质含量的关系
表1 研究区2种主要岩性的关于式(5)的参数统计Table 1 The parameters of formula (5) for two main lithology in the study area |
| 岩性 | 系数D | 系数E | 系数n |
|---|---|---|---|
| 细砂岩 | 0.286 4 | 1.190 1 | 1.59 |
| 粉砂岩 | 0.311 6 | 1.136 3 | 1.56 |
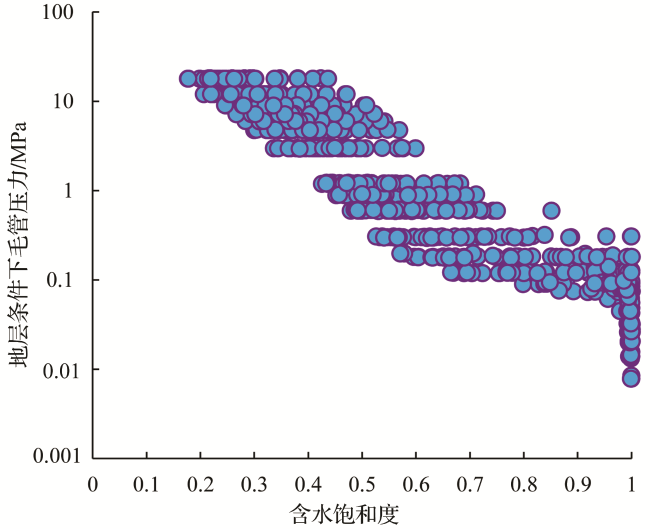
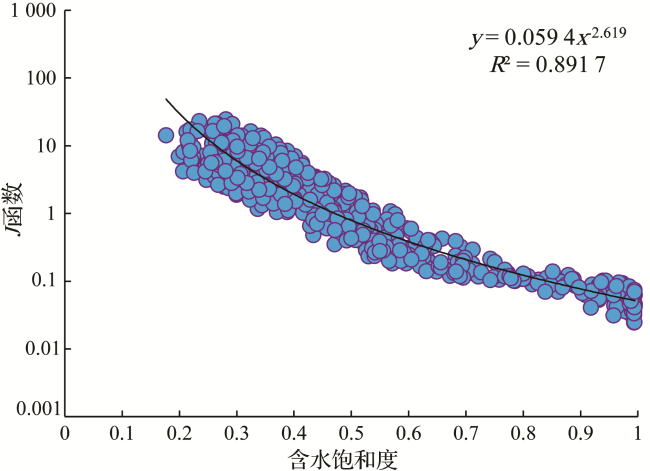
2.2.2 含水饱和度的确定
2.2.3 孔隙度计算模型的确定
表2 研究区2种主要岩性的关于式(12)的参数统计Table 2 The parameters of formula (12) for two main lithology in the study area |
| 岩性 | 系数D | 系数E | 系数F |
|---|---|---|---|
| 细砂岩 | 0.286 4 | 1.190 1 | -0.607 4 |
| 粉砂岩 | 0.311 6 | 1.136 3 | -0.595 9 |
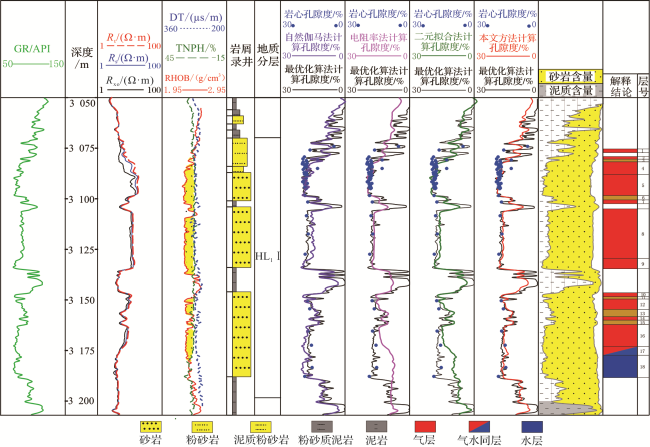
3 应用实例
表1 F气田X井孔隙度计算误差统计Table 1 Statistics of errors in porosity calculation of Well X in F Gas Field |
| 层 号 | 深度/m | 录井 岩性 | 岩心分析 孔隙度/% | 测井计算孔隙度/% | 相对误差/% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | σ1 | σ2 | σ3 | σ4 | |||||
| 1 | 3 075.4~3 077.2 | 粉砂岩 | 14.9 | 10.9 | 13.4 | 11.2 | 11.9 | 14.3 | -23.8 | -6.3 | -21.7 | -16.8 | |
| 2 | 3 079.1~3 080.4 | 粉砂岩 | 18.6 | 16.1 | 14.5 | 14.0 | 15.4 | 17.6 | -8.5 | -17.6 | -20.5 | -12.5 | |
| 4 | 3 081.7~3 088.0 | 粉砂岩 | 17.2 | 17.1 | 17.7 | 17.9 | 17.6 | 17.3 | -1.2 | 2.3 | 3.5 | 1.7 | |
| 5 | 3 088.0~3 098.4 | 细砂岩 | 19.1 | 18.4 15.8 15.6 19.4 18.3 16.7 15.6 17.8 18.8 18.3 | 18.5 | 19.4 | 18.8 | 18.6 | -1.1 | -0.5 | 4.3 | 1.1 | |
| 7 | 3 100.5~3 102.4 | 细砂岩 | 17.3 | 14.2 | 13.9 | 14.1 | 16.4 | -3.7 | -13.4 | -15.2 | -14.0 | ||
| 8 | 3 105.1~3 129.5 | 细砂岩 | 17.8 | 17.2 | 16.1 | 16.9 | 17.2 | -9.3 | 0.0 | -6.4 | -1.7 | ||
| 9 | 3 129.5~3 134.6 | 细砂岩 | — | 17.8 | 18.3 | 18.3 | 18.1 | 7.2 | -1.7 | 1.1 | 1.1 | ||
| 10 | 3 146.4~3 148.4 | 细砂岩 | — | 16.1 | 16.5 | 16.8 | 17.4 | 5.2 | -7.5 | -5.2 | -3.4 | ||
| 12 | 3 149.5~3 154.7 | 细砂岩 | 16.7 | 15.1 | 15.1 | 16.2 | 16.1 | 3.7 | -6.2 | -6.2 | 0.6 | ||
| 14 | 3 158.3~3 160.0 | 细砂岩 | — | 14.0 | 13.3 | 15.0 | 16.1 | -3.1 | -13.0 | -17.4 | -6.8 | ||
| 16 | 3 162.2~3 173.1 | 细砂岩 | 16.1 | 14.0 | 14.5 | 16.1 | 16.4 | 8.5 | -14.6 | -11.6 | -1.8 | ||
| 17 | 3 173.1~3 177.3 | 细砂岩 | — | 9.1 | 11.8 | 15.6 | 16.9 | 11.2 | -46.2 | -30.2 | -7.7 | ||
| 18 | 3 177.3~3 188.4 | 细砂岩 | 17.5 | 8.0 | 9.6 | 16.1 | 16.9 | 8.3 | -52.7 | -43.2 | -4.7 | ||
|



 甘公网安备 62010202000678号
甘公网安备 62010202000678号