0 引言
然而，无论是干燥煤样或平衡水煤样进行的等温吸附实验，均采用Langmuir吸附理论，该理论为假设系统中仅存在固相与气相的固—气界面吸附理论，但实际煤层气储层富含大量的液相水，这会使采用Langmuir吸附理论的结果与实际产生较大的误差。因此，本文从煤储层的热演化过程出发，论证煤储层孔隙中液相水存在的普遍性，并进一步建立了考虑煤储层气水分布的不同基质含水饱和度下的解吸曲线方程。
1 煤储层的水环境
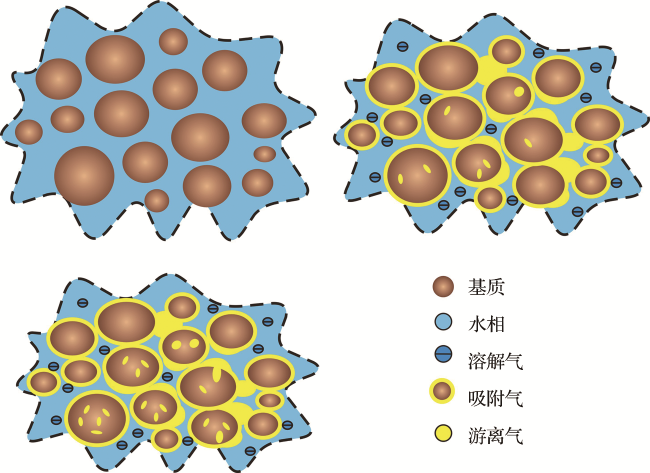
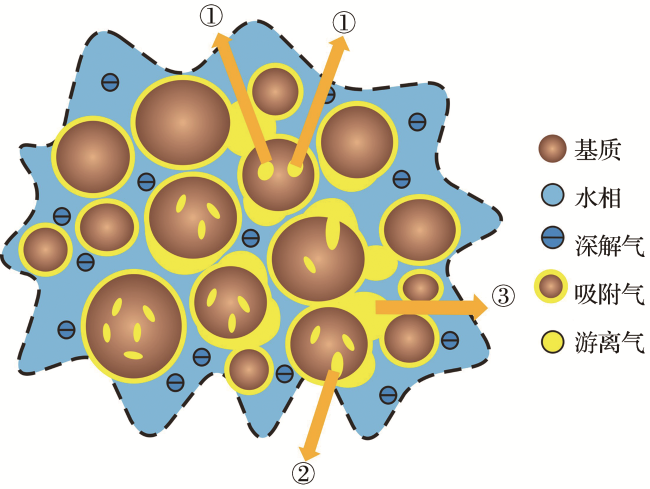
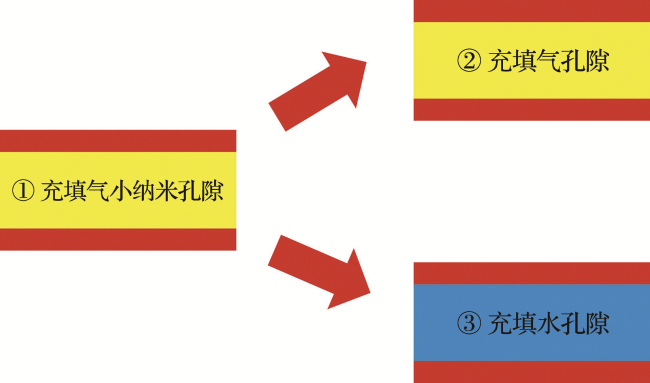
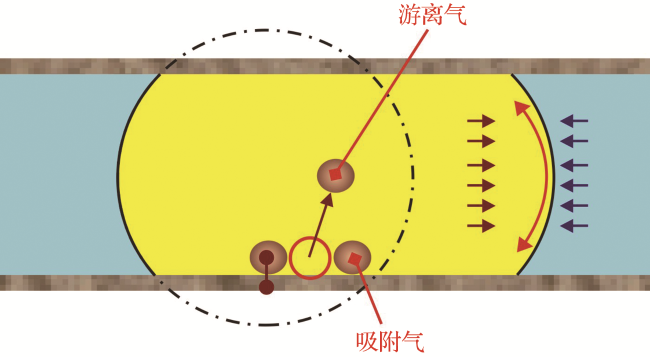
1.1 煤岩孔隙气水赋存演变特征
随着热演化的进一步进行，更多的气相开始生成，这一方面会造成原生孔隙中气相所占比例进一步提升；另一方面会使得原先因为毛管力影响无法排出的气孔中的气相压力增大直至克服毛管力，或进一步憋裂煤岩形成新的渗流通道，最终使得越来越多的气孔与原生孔隙相连通，更多的气相进入原生孔隙甚至割理，煤岩孔隙的气水赋存演变过程示意见图1。
由此，可以获得煤储层在具有开发价值时的微观气水分布特征，并由此可以进一步获得开发过程中煤储层中气相进入割理的主要运移路径，如图2所示：①气孔中的解吸气和游离气进入原生孔隙后进入割理和裂隙；②气孔中的解吸气和游离气直接进入割理和裂隙；③原生孔隙中的解吸气和游离气直接进入割理和裂隙。
考虑到煤层气储量以吸附气为主，且吸附气大多富集于纳米级小孔隙中，因此假设较大孔隙原生孔隙和气孔中的游离气均是由小纳米孔隙中运移而来的，由此可将运移路径简化为：①小纳米孔隙中的气相进入充填液相原生孔隙后进入割理和裂隙；②小纳米孔隙中的气相进入充填气液两相原生孔隙后进入割理和裂隙；③小纳米孔隙中的气相进入充填气相孔隙后进入割理和裂隙。
1.2 煤岩基质液相水影响孔隙所占比例
为了便于计算，采用毛管束模型模拟气相运移路径，其中小纳米孔隙与其他孔隙分别等效为一个毛管束，两个毛管束相互串联，气相由代表小纳米孔隙的毛管束单向的流入代表其他孔隙的毛管束。再将气相经由气液两相孔隙排出基质的过程等效为气相经由气相孔隙和气相经由液相孔隙排出基质两部分的耦合过程，由此，我们可以获得理想条件下基质液相水影响孔隙所占比例的毛管束模型，由此有助于之后对液相水的影响进行量化。
令f(r)为煤储层孔隙半径为r的孔径所占的比例，测定的含水饱和度S w为基质和裂隙中总的含水饱和度，f w为基质孔隙中的含水饱和度，则含水饱和度与煤储层中单相渗流通道所占的比例直接的关系可以由图3体现。
可以看出，基质孔隙的含水饱和度f w是煤储层基质中整体的含水饱和度，即①+②+③的含水比例，而实际煤储层中受液相水影响的基质孔隙为两相渗流通道占所有渗流通道的比例，即③占②+③的比例，因此需要对基质含水饱和度进行修正。
由于煤岩的吸附过程主要发生在小于一定尺度的纳米孔隙中，定义该尺度为r c，根据模型的假设条件，小于r c的孔隙即为左边的气孔孔隙①，而大于r c的孔隙则可能为气孔原生孔隙，即为右侧的②、③。因此，根据煤储层孔隙半径为r的孔径所占的比例，以及储层中最大孔隙半径为r max和最小孔隙半径为r min，可以计算①、②、③所代表的孔隙分别所占体积及煤岩孔隙总体积。
根据基质孔隙中的含水饱和度f w的定义，其等于煤岩孔隙总体积与含水孔隙总体积的比值，即：
由此可以分别获得②和③所占孔隙体积：
考虑到实际渗流过程中①与②、③串联，则两相渗流通道①、③连通所占的比例。
2 不同含水饱和度环境下的解吸数学模型
2.1 100%液态水环境下模型
针对液态水环境下甲烷分子进行分析，认为甲烷分子在液态水中存在吸附—解吸和溶解—脱溶2个化学过程，因此可以认为在煤储层固—液界面解吸过程中，存在2个平衡体系。
(1)液态环境中溶解与脱溶的再平衡问题：压力降低致使甲烷在水中的溶解度S降低，孔隙水呈现过饱和状态，从而溶解态甲烷分子脱溶，部分溶解气析出。
(2)液态环境中吸附与解吸的再平衡问题：溶液在整个解析过程中呈现过饱和状态，解吸的甲烷分子存在聚集力与吸附力的相互作用，仅有能量较大的甲烷分子可以成核、成泡，大部分甲烷分子难以解吸[9]。
式中:r *为Gibbs自由能达到最大时的临界半径，可由接触角θ计算获得，r *=r/cosθ；V des为解吸气量;P des为解吸压力;P ads为对应吸附状态下的压力，即实际过程中的压力;P c为毛管力。根据公式可以计算得到100%含水条件下的解吸曲线。
由此，可确定饱和含水条件下甲烷解吸与压力之间的关系，与Langmuir固—气界面吸附/解吸理论相结合，联立考虑煤层气气水分布数学表征，假设煤层气中含气区域满足固—气界面解吸，含水区域满足固—液界面解吸，由此便可获得不同含水下煤层气的宏观解吸特征。
2.2 不同含水条件下模型
通过气体分子的分子间作用力，可以建立100%含水条件下的气体解吸数学模型，然而实际煤层气储层气水分布极为复杂，不可能出现100%含水条件，气体均吸附在储层固相颗粒上的气水分布情况，因此，需要对100%含水条件下的气体解吸数学模型进行修正，获得不同含水饱和度环境下的解吸数学模型。
2.2.1 模型建立
假设煤层气中含气区域满足固—气界面解吸，含水区域满足固—液界面解吸，同时在解吸过程中，考虑由于解吸气产生造成单相气毛管比例和气相毛管中压力的变化，最终的解吸气量可由下式计算。
式中: 为原始气相孔隙所占比例， 为解吸气膨胀驱替原始含水孔隙空间后所增加的气相孔隙所占比例; 为利用Langmuir固—气界面吸附曲线计算出的气相孔隙空间解吸气量; 为利用100%液相水含量下的解吸曲线计算出的液相孔隙空间解吸气量，公式(10)中的 为降压解吸时降低到的压力; 为考虑储层孔隙毛管力及解吸气膨胀造成气相毛管中压力变化后的压力。
式中： 为膨胀的气体体积，可由下式计算：
而考虑储层孔隙毛管力及解吸气膨胀造成气相毛管中压力变化后的压力 的计算方法如下：
可以看出，计算最终解吸气量V所需的必须参数均为与V有关的函数，因此需要采用迭代法进行求解，迭代的具体思路如下：
(1)假设煤储层中解吸出的气既不会造成含气区域的碰撞，也不会造成含气区域压力的变化，由此可利用吸附方程计算原始含气区域所占比例及压力下所对应的解吸气量。
(2)将计算出的解吸气量与含气区域所能容纳的最大含气量进行对比，并认为多余的气量用于使含气区域扩大，但最大不能超过当前压力所能克服的最小孔隙半径。
式中: 为当前压力所能通过的最小毛管的孔喉半径， 。
（3）含气区域扩大后仍多余的气相将会导致气相区域的压力提高，由此可以利用PVT方程计算出气相区域新的压力。
（4）利用方程计算新的含气区域所对应的解吸气量，不断循环直至计算出的解吸气量能被含气区域所容纳。
由此可以获得该含水饱和度下的气体解吸曲线，通过改变不同的含水饱和度，即可获得不同的解吸曲线。
2.2.2 模型验证
为了验证模型可靠性，本研究设计并开展了甲烷在不同程度含水煤样样品的吸附能力实验。值得注意的是：在常规研究中，主要对比样品在平衡水条件（环境湿度RH=98%）与干燥条件下的甲烷吸附能力；而在本研究中，在进行解吸实验之前，优先采用不同的注入压力向煤岩中注入液相水，并有以下假设。
（1）不同压力的注入过程中煤岩孔隙结构不发生变化，即不同液相水注入压力对煤岩孔隙的破坏作用相同，由此造成不同注入过程后煤岩最终孔喉结构保持不变。
（2）当注入过程达到稳定，即注入水量与产出水量达到平衡时，所有孔喉半径对应毛管力小于注入压力的孔隙均被水充填，由此模拟实际煤层气储层中微纳米孔隙以充填气相的气孔为主，较大孔隙以充填液相的原生孔为主的孔喉气水分布特征。
最终不同含水的等温吸附实验均放置在IMI高温高压吸附/解吸仪中进行（图5），吸附气体采用纯度大于99.99%的甲烷气体。考虑到甲烷吸附测试耗时较长且水分在高温条件下容易蒸发，本文研究仅进行了室温（25℃）甲烷吸附测试。由于实验釜在20MPa下的气密性较好，实验误差较小.在甲烷吸附测试之前，仪器进行抽真空，并利用氦气标定参考釜及实验釜体积，此过程持续时间为12h左右。
针对煤样注入液相水的处理，分别选用了1.5MPa、7.2MPa和14.5MPa 3个不同的注入压力，以模拟低含水、中含水、高含水不同条件下的解吸过程。
为了减少在进行孔喉分布实验中对实验煤样的损害，因此假设煤样孔喉分布满足分形分布，建立理想的煤岩气水分布模型，并利用下式计算不同注入压力对应的基质含水饱和度。
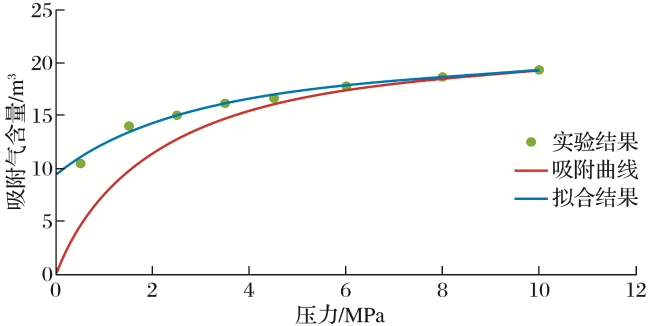
图6 1.5MPa注入液相水后吸附曲线与模型拟合对比Fig.6 Adsorption curve and model results in 1.5MPa inject |
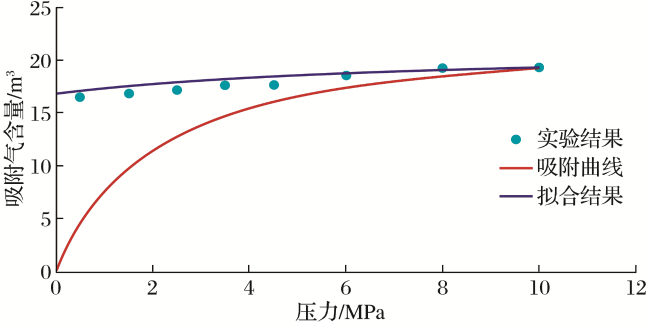
图7 7.2MPa注入液相水后吸附曲线与模型拟合对比Fig.7 Adsorption curve and model results in 7.2MPa inject |
通过对比可以发现，最终拟合结果与实验结果具有较好的拟合效果，说明该模型具有可靠性。
对该模型计算过程中的误差进行分析，影响实验误差的因素主要有2个：
(1)模型所必须的孔喉分布参数难以准确描述实际储层。常用的获得模型必须的孔喉分布参数的方法有2个，孔喉分布实验（即压汞实验/压液氮实验）以及理想的分形模型法，均无法准确获得实际煤岩储层孔喉分布特征。这是因为对于实验而言，由于压入分子半径的约束，小于该半径的孔喉尺度分布的纳米孔隙无法被测得，而对于煤岩而言，纳米尺度的孔喉分布才是最主要的;另一方面，实验过程中为了保证流体的压入采用过大的压差，势必会对力学性质较差的煤岩产生不可逆的伤害，由此获得的最终孔喉分布将不再是煤岩原始储层孔喉分布，而是被实验压力破坏后的孔喉分布。而对于理想的分形模型而言，实际储层很难真正与模型分布相似，势必会存在较大误差。
(2)在利用注入法获得不同基质含水饱和度的煤样时，较大的注入压力势必会对煤岩造成破坏，影响最终的实验结果。
2.2.3 模型结果分析
建立理想条件下不同基质含水饱和度下的解吸曲线图版，如图9所示。
通过分析计算结果可以发现，随着基质含水饱和度的增加，解吸滞后现象越来越明显。这是由于一部分压降用来克服毛管力和液相解吸成核。同时随着基质含水饱和度的增加，解吸后的残余气体越来越多。这是由于液相中的吸附气极难被解吸。
另一方面，解吸曲线在低含水饱和度和高含水饱和度时对含水饱和度敏感，这是因为低含水饱和度时，气液解吸能力为影响解吸的主控因素。低含水下，极低的含水增加都意味着有新的毛管从气相充填变为液相充填，大大影响解吸能力；高含水饱和度时，液相水导致的解吸气难产出是主控因素。由于高含水下气孔往往与充填液相水的孔相连，此时产出的气必须克服两相间毛管力才能被产出，因此随着含水增加，解吸气量显著下降。
与此同时，对于理想的分形孔喉分布而言，当基质含水饱和度达到70%时，孔隙内的气体已经很难解吸，且解吸出的气体与原本纳米孔隙内的气体由于毛管力的约束无法脱离纳米孔隙，表现在宏观解吸曲线上即为解吸量为0，因此，对于实际储层而言，一定量的游离气是保证降压后存在宏观解吸气的根本，一方面游离气所对应的Langmuir固—气界面解吸要远远容易与固—液界面解吸，另一方面游离气使得微观解吸出的气体在宏观体现出来所需克服的毛管力越小。
最后，将考虑液相水后不过坐标原点的解吸曲线与Langmuir过原点的吸附解吸曲线，以及利用参数修正法获得的过原点的不同含水饱和度下的吸附解吸曲线进行对比，可以发现在远离原点段，曲线具有相同的特征，仅仅在近原点段存在较大误差，因此采用过0点的Langmuir曲线或参数修正法解吸曲线进行研究，会出现总体拟合效果很好，但在接近0点时存在误差极大的现象，由此，采用过0点的Langmuir曲线或参数修正法解吸曲线进行生产动态拟合和预测时可能可以获得较好的效果，但计算储层含气量会产生极大的误差。
因此，对于确定的煤层气储层，可采储量中吸附气的计算精度与液相水含量息息相关，液相水含量越高，一方面固—液界面吸附解吸所占比例越高，气体越难以被解吸；另一方面微纳米孔隙解吸出的气体由于毛管力的作用越难以被产出，宏观上无法体现。
3 结论
(1) 刻画了煤储层的气水分布特征，为建立煤层气孔隙气水分布模型提供了基础。基于对煤储层孔隙特征及热演化过程的分析，认为煤层气孔隙中参与生产渗流的纳米孔隙主要以气孔为主；且气孔中充填单相气相，其余孔隙初始为单相水相，随着煤的热演化程度增加，部分孔隙中的水相被成煤作用中生成的甲烷气相所驱替，根据孔隙壁的物理性质及孔隙尺寸，形成单相气相或复杂的气水两相。
(2) 建立了煤层气储层孔隙的气水赋存模型。利用煤储层的孔隙分布特征，建立了煤层气储层孔隙的毛管束模型，利用串联的2组毛管束分别代表纳米尺度的气孔孔隙和其他孔隙，表征了煤层气储层的气水分布特征，并由此可以求出不同条件下煤层气储层中气相孔隙和气水两相孔隙所占的比例，为进一步建立考虑气水分布的煤层气解吸模型提供了基础。
(3) 建立了吸附解吸曲线受气水分布的数学模型。利用建立好的煤层气孔隙气水分布模型，考虑由于解吸气产生造成单相气毛管所占比例和气相毛管中压力的变化，利用迭代法得到液相水含量对煤储层解吸曲线的影响模型，最终获得的模型与实验结果具有较好的拟合结果。
(4) 评价了液相水含量对煤储层解吸曲线的影响。利用建立的液相水含量与解吸曲线的关系模型，计算相同条件不同液相水含量下的解吸曲线，发现随着液相水含量的增加，解吸滞后现象越来越明显。这是由于一部分压降用来克服毛管力和液相解吸成核，同时随着液相水含量的增加，解吸后的残余气体越来越多，这是由于液相中的吸附气极难被解吸。
甘公网安备 62010202000678号
