引用本文

Zhao Jun，Yang Yang.Porosity calculation method for CO2-containing gas reservoirs[J].Natural Gas Geoscience,2016,27(4):571-576.[赵军，杨阳.含CO2气层孔隙度计算方法[J].天然气地球科学，2016,27(4):571-576.]
doi:10.11764/j.issn.1672-1926.2016.04.0571

含CO2气层孔隙度计算方法

更多

赵军 ，杨阳 

（西南石油大学地球科学与技术学院，四川成都610500）

作者简介：赵军（1970-），男，四川成都人，教授，博士，主要从事岩石物理及其解释与评价研究.E-mail：zhaojun_70@126.com.

基金项目：国家“十二五”科技重大专项子课题“莺琼盆地高温高压地层岩石地球物理特征与地震属性技术研究”（编号：2011ZX05023-004-02）资助.

摘要  
南海西部海域莺琼盆地为高温高压高含CO2含油气盆地,在储层测井评价孔隙度计算过程中，由于气、水性质的差异，若用岩心刻度法求取储层孔隙度，会导致计算的孔隙度值不能反映地层的真实情况，对此，提出联合体积物理模型和阿尔奇公式的方法求解含气储层孔隙度。此外，考虑到研究区CO2的影响，首先将CO2对流体密度以及地层水电阻率的影响进行了分析，然后确定相应的计算参数。应用表明，该联合求解孔隙度的方法较简洁，且解释结果与经覆压校正后的岩心孔隙度吻合较好，平均误差为5.81%，满足该区储层评价的要求，说明了该方法的可靠性。该方法可为高温高压高含CO2含气储层测井孔隙度计算提供一种新的选择。

关键词： 孔隙度       CO<sub>2</sub>       体积物理模型       阿尔奇公式       联合       岩心刻度      

中图分类号:TE122.2      文献标志码:A      文章编号:1672-1926(2016)04-0571-06

Porosity calculation method for CO2-containing gas reservoirs

Zhao Jun ，Yang Yang 

（School of Geoscience and Technology,Southwest Petroleum University,Chengdu 610500,China）

Abstract  
Yingqiong Basin in western of South China Sea is a hydrocarbon-bearing basin,with high temperature and high pressure,as well as CO2.In the process of reservoir porosity calculation,due to differences in gas and water properties,if we choose the method of core calibration,the calculated result of porosity will not reflect the real situation of formation.To solve this problem,a new method was put forward: to combine physical model and Archie’s method to calculate the porosity of gas reservoir.Moreover,the impact of the CO2 was also taken into consideration: the effect of CO2 on density and formation water resistivity.The processing of some practical data was used to illustrate the effect of this method.The result shows a good accordance between logging’s porosity and core porosity corrected by using the method of core overburden pressure,and the average error is 5.81 percent.This method provides a new option for logging to calculate porosity in CO2-containing gas reservoirs.

Key words： Porosity;       CO<sub>2</sub>;       Physical model;       Archie’s method;       Combine;       Core calibration;      

引言

利用常规测井计算储层孔隙度时，对于砂泥岩地层，当储层孔隙中只含有油,水两相时，考虑到油和水的密度以及纵波时差值差别不大，故可以采用岩心刻度法[1,2]，即建立密度或纵波时差值与岩心分析孔隙度的对应关系来求取储层孔隙度[3-5]。但研究区位于南海西部海域莺琼盆地，天然气资源丰富[6]，由于天然气与水的密度和纵波时差差别较大，不能在密度和纵波时差上将流体看作单一流体，如果继续使用岩心刻度法则可能使求出的孔隙度偏离真实孔隙度。针对此问题，本文提出利用考虑流体成分的岩石体积物理模型[7]，再联合饱和度计算经典公式——阿尔奇公式[8,9]，共同求解含气储层孔隙度。 此外，经过多年的勘探实践活动，已在莺琼盆地的多个构造带上发现了具有工业价值的高温高压高含CO2气层[10]。由于高温高压条件下CO2与CH4混合气体对岩石声学、电学性质及其变化规律仍然认识不清，尤其是CO2的附加导电性对岩石电阻率影响的认识仍然是空白，导致测井解释孔隙度计算精度难以保障。为了提高高温高压高含CO2气藏的勘探开发效率，准确地求取储层孔隙度显得尤为重要[11-13]。 对此，本文首先将CO2对流体密度和地层水电阻率的影响进行了分析，然后再建立相应的孔隙度计算模型。该优化的孔隙度测井解释方法，提高了现有高温高压高含CO2气藏测井解释模型的精度，在研究区得到了很好地运用。

1 联合体积物理模型—阿尔奇公式计算孔隙度方法

1.1 基于密度体积物理模型的储层孔隙度计算方法

1.1.1 岩石骨架密度的确定

对DF13-1区(DF13-1-2井共75块岩心或岩屑)和DF13-2区(DF13-2-6井共28块岩心)的薄片数据进行分析，统计其中各种矿物成分的含量，运用体积物理模型的方法求取岩石骨架密度，计算公式如下(分析结果如表1)：

B=∑i=1nBi·Vi(1)
式(1)中：B、Bi分别为骨架密度、骨架各组成部分密度,g/cm3；Vi为骨架各组成部分占骨架总体积比例。

1.1.2 岩石流体密度的确定

流体密度可以直接通过高温高压实验模拟地层温压条件(据统计分析，研究区温压条件分别平均为150℃、50MPa)，来测量单种流体或多种混合流体的密度值。 本文同样选用体积物理模型的方法来计算岩石流体密度，在建立密度体积物理模型时，使用含14%CO2的CH4作为气体骨架密度，未将2种气体分开单独求解各自含量，原因是：①若增加地层 组分，无法构成恰定或超定方程组，造成多解；②将CO2单

表1     岩石骨架参数
Table 1     The list of rock matrix parameters
资 料薄片分析矿物含量统计结果/%计算结果
矿物密度/(g/cm3)DF13-1区DF13-2区DF13-1区DF13-2区
石英2.657574.8骨架密度：2.663g/cm3 骨架密度：2.652g/cm3
钾长石2.5665.9
钠长石2.605--
钙长石2.77--
钡长石2.77--
白云石2.87--
硬石膏2.96--
石膏2.32--
方解石2.7144.2
黄铁矿4.7--
菱铁矿3.8--
铁白云石2.987.8
白云母2.826.46.2

注：“-”表示不含或微量

独作为流体成分之一会增大地层组 分复杂性，使孔隙度计算的精度难以保证；③经过MDT测试，已钻遇气层中大部分CO2含量在14%左右，故本文折中使用含14%CO2的甲烷气体作为气体骨架密度的平均值。表2为模拟地层条件(150℃、50MPa)测量和计算得到的流体参数值.

1.1.3 密度测井计算孔隙度模型建立

依据泥质砂岩气层的岩石体积物理模型,其密度测井的响应方程为[7] :

ρma(1-φ-Vsh)+ρgφ(1-Sw)+ρwφSw+ρshVsh=ρb(2)
化简后，提取未知参数后可得：
ρb-ρshVsh=ρwφw+ρma(1-φ-Vsh)+ρg(φ-φw)(3)
式中:ρma、ρg 、ρw和ρsh分别为纯砂岩骨架、气体、地层水和泥质的密度；φ、φw分别为总孔隙度、含水体积；Sw为含水饱和度；Vsh为泥质含量。 式(3)中共有总孔隙度φ和含水体积φw2个未知参数，仅用一个体积物理方程无法全部求解。但需要注意的是，总孔隙度φ和含水体积φw之间存在一个含水饱和度Sw的关系，因此，可以联立阿尔奇公式，同时求出上述2个未知参数。

1.2 基于阿尔奇公式的储层孔隙度计算方法

1.2.1 CO2 对地层水电阻率的影响分析

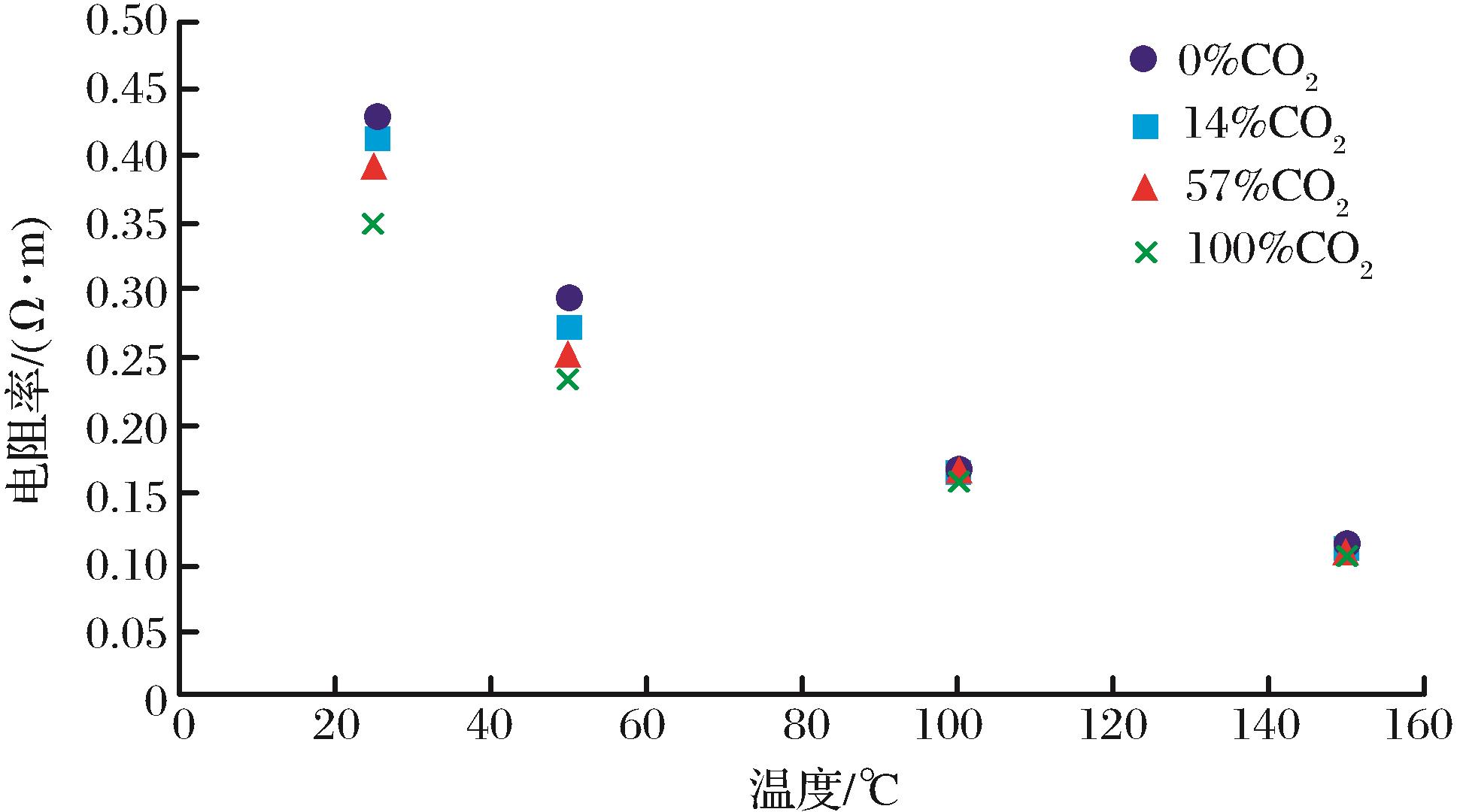
从实验可知，地层水电阻率受温度影响明显，而受压力影响很小，故本文重点研究温度对地层水电阻率的影响。考虑到部分储层中含有CO2，CO2在水中溶解并电离后可能会对地层水电阻率造成影响，为探索高含CO2气体储层的地层水电阻率变化情况，在不同温度下向装有矿化度为13 000mg/L(模拟研究区地层水矿化度)地层水的容器中分别持续通入纯CH4和纯CO2，保持压力为50MPa(模拟研究区孔压条件)不变，待气体溶解充分后，取水样测试电阻率，所得结果如图1所示.

图1     不同温度下不同含量CO2的混合气体溶于水后的电阻率值对比
Fig.1     The comparision of water resistivity values after different content of CO2 mixed gas is dissolved in water at different temperatures

从图1中可以看出，各个温度下，CO2含量越高，电阻率降低越大；且在温度较低(如25℃)时，不同含量CO2溶于水所对应地层水电阻率差异较大，随着温度升高，差异逐渐减小；当温度达到150℃时，各地层水电阻率已经非常接近。故可知，混合气体CO2溶度越高，对地层水电阻率影响越大；且随着温度升高，CO2溶解对地层水电阻率的影响会逐渐减小。 此外，为了定量分析高温高压条件下CO2溶于水对地层水电阻率的影响，本文拟合出了电阻率降低量的极大值的数学计算式：根据图1数据，计算出不同温度下通入气体为100%CO2 ，且完全溶于水时地层水电阻率降低百分比ΔRw，拟合成随温度T变化的公式为：
ΔRw=Rw·8.96T+23.28(4)
式中：Rw为无CO2地层水电阻率，Ω·m；ΔRw为100%CO2溶解导致的地层水电阻率降低百分比，%；T为温度，℃。 由式(4)也可知，随着温度T的升高，地层水电阻率降低百分比ΔRw减小，与上述分析结果相同，且运用该式可计算出在研究区储层平均最低温度(T=130℃)下，(ΔRw)max=5.9%，故可知，在研究区储层条件下(130～150℃)CO2对地层水电阻率降低的影响最大不超过5.9%。说明在高温高压条件下，CO2溶解并电离对地层水电阻率的改变微乎其微，故在利用阿尔奇公式计算储层孔隙度时，不考虑CO2对地层水电阻率的影响。

1.2.2 阿尔奇公式计算地层孔隙度

运用阿尔奇公式求取含水饱和度的表达式为：

RtRw=abφmSwn(5)
两边同时取对数可得：
nLgSw=LgabRwRt-mLgφ(6)
将Sw进行转化后可得：
(m-n)Lgφ+nLgφw=LgabRwRt(7)
通过岩电实验可得4个岩电参数a、b、m、n的值，且通过地层水分析资料可以求出地层水电阻率Rw。因此，式(7)中同样含有总孔隙度φ和含水体积φw2个未知参数，可以联合上式(3)共同求解2个未知参数。

1.3 联合体积物理模型—阿尔奇公式计算孔隙度

由上述可知，联立式(3)和式(7)2个未知方程后，可同时求解总孔隙度φ和含水体积φw2个未知参数。此外，由于式(7)中存在对数，故无法简单地求解这2个未知数。因此，本文采用赋初值并以一定步长循环的原理对这2个未知数进行离散化数值求解，具体步骤是： (1)对总孔隙度赋初始值φ=0。 (2)对含水体积赋初始值φw=0，然后以0.1为采样间隔，对含水孔隙度进行扫描取值，含水孔隙度的最大值为φw=φ，然后通过程序自动确定一组使得式(3)和式(7)误差最小的解，作为本文(φw,φ)的数值最优解。 (3)φ=φ+0.1，当φ=30%，循环结束；否则重复上述步骤(2)。 (4)从步骤(2)中提取出每组使得式(3)和式(7)误差最小的解(φw,φ)，优选出误差最小的一组解(φw,φ)，作为本文含水体积φw和总孔隙度φ的数值最优解。

2 算法精度检验

通过实验可得到该区岩心孔隙度覆压校正公式：

φc=0.969 4φ-0.457 2(8)
式中：φ为覆压校正之前的岩心孔隙度，%；φc为覆压校正之后的岩心孔隙度，%。 对研究区12口井总共620块岩心和壁心按照式(8)作覆压校正，然后用经覆压校正后的岩心孔隙度与利用本文所述方法计算的孔隙度作对比，以验证其准确度（图2）。 图2为研究区12口井620块岩心和壁心测井计算孔隙度与岩心覆压校正后孔隙度对比交会图。图中黑色线为坐标系的45°线，落在此线上的点表示测井计算孔隙度与岩心覆压校正后孔隙度相等，2条绿色线表示孔隙度介于±8%的误差线。从图2可以看出，利用上述联合求解方法计算的孔隙度与岩心覆压校正后的孔隙度基本落在±8%的误差线之内，说明了计算的孔隙度与岩心孔隙度相比误差较小。且经计算可知，所有岩心和壁心的覆压校正后的孔隙度与测井计算孔隙度的平均误差为5.81%，由此证实，基于本文提出的方法计算的孔隙度能够满足该区储层评价和储量计算的要求。

3 应用效果评价

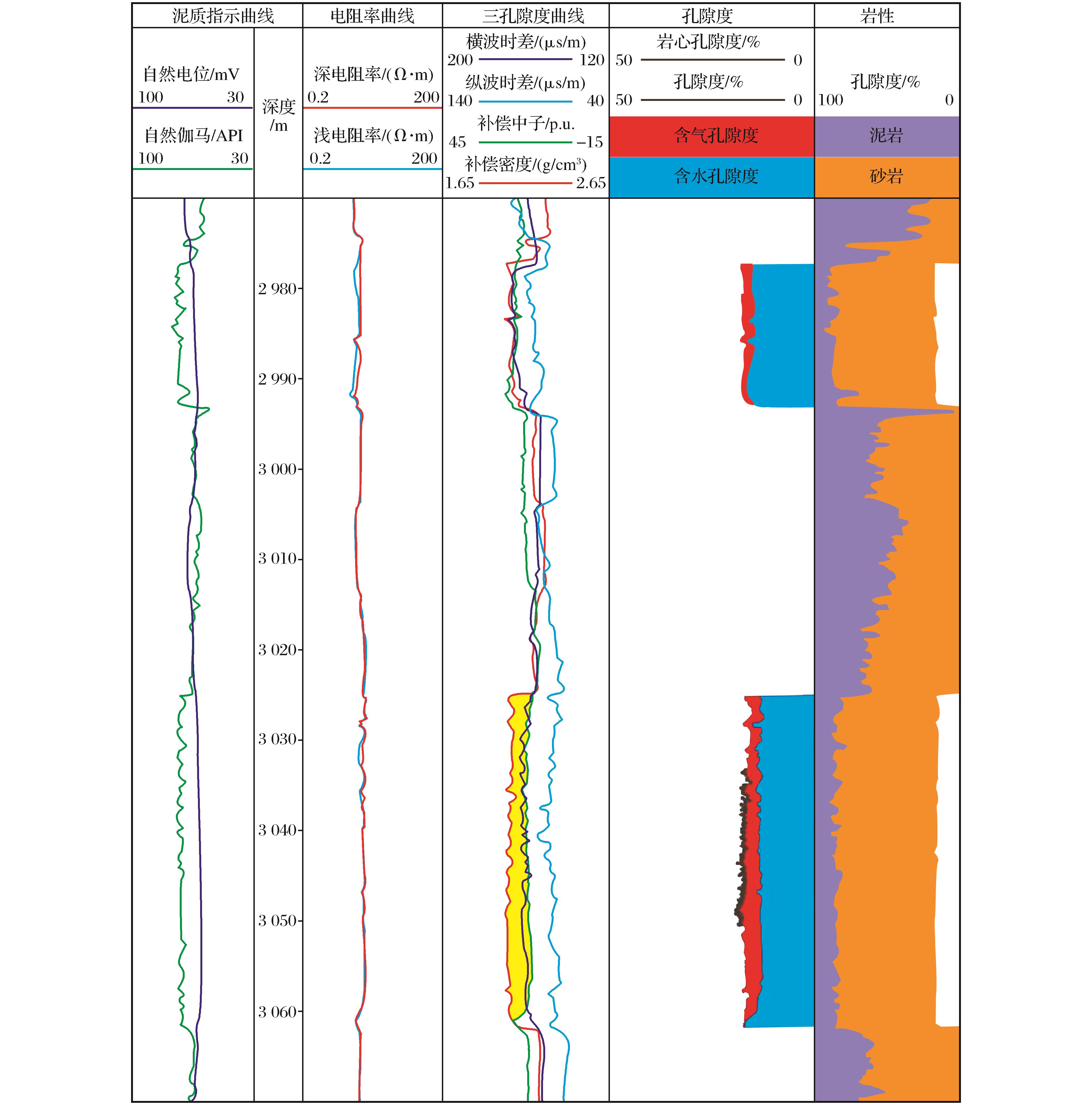
利用本文方法对研究区DF13-1-2井(2 970～3 070m)段进行实际资料处理，计算的地层孔隙度与岩心孔隙度对比结果如图3所示。图中第4栏为利用本文所述方法计算的储层总孔隙度与岩心孔隙度之间的对比，从该栏可以看到储层总孔隙度被分为含气孔隙度和含水孔隙度，此外，从总孔隙度和岩心孔隙度的对比可以看到(2 987～2 993m和3 025～3 062m段)，岩心孔隙度（图中用小黑点表示）大致分布在总孔隙度附近，两者吻合较好，由此再次证实,基于本文提出的方法计算的储层孔隙度能够较准确地反映实际地层的真实孔隙度。

图2     测井计算孔隙度和岩心覆压校正后孔隙度交会
Fig.2     The cross plot of logging calculated porosity and core porosity after overburden pressure correction

4 结论

(1)由资料统计以及为了简化模型计算量，在建立密度体积物理模型时，本文使用含14%CO2的甲烷气体作为气体骨架的平均密度。 (2)在高温高压条件下，CO2对地层水电阻率降低的影响最大不超过5.9%，且随温度升高，影响越小，故本文在利用阿尔奇公式计算储层孔隙度时，不考虑CO2对地层水电阻率的影响。 (3)单独使用体积物理模型求解储层孔隙度时，由于含有2个未知参数，无法求得方程解。通过分析2个未知参数φw和φw与Sw存在转换关系，可以联想到联立阿尔奇公式共同求解未知参数。该方法的优势在于避免了利用单一方法计算孔隙度时首先要获取地层含水饱和度、含水体积等参数的问题，简化了测井解释计算量。 (4)通过对研究区含气水层的实际资料处理，证实本文提出的方法在计算孔隙度方面，计算的孔隙度与经过覆压校正后的岩心孔隙度吻合较好，且其误差范围满足含气储层评价和储量计算要求，能够真实地反映储层的孔隙度。

图3     DF13-1-2井孔隙度解释成果
Fig.3     The results of porosity logging interpretation of Well DF13-1-2

参考文献(References)



[1] Zhao Jun,Chen Fuxuan.The application of core calibration method in logging interpretation model[J].Xinjiang Petroleum Geology,1998,19(5):421-423.[赵军,陈福宣.岩心刻度法在测井解释模型中的应用[J].新疆石油地质,1998,19(5):421-423.]

[2] Qin Qirong.The application and research of the analyses of the whole diameter sample in the explanation of crack porosity:Taking the Permian crack reservoir for example in the area of Bai 31,in the Kelamayi Oil Field[J].Natural Gas Geoscience,2005,16(5):637-640.[秦启荣.全直径样品分析在测井解释裂缝孔隙度中的应用研究——以克拉玛依油田百31井区二叠系油藏为例[J].天然气地球科学,2005,16(5):637-640.]

[3] Li Shurong,Li Aihua,Qian Qin,et al.An approach to calibrate logging porosity with whole well cores data[J].Well Logging Technology,2010,34(6):572-575.[李淑荣,李爱华,钱勤,等.利用全直径岩心刻度测井孔隙度方法探讨[J].测井技术,2010,34(6):572-575.]

[4] Zou Liangzhi,Xie Ranhong.The application of core in establishing logging interpretation model[J].Journal of Oil and Gas Technology,2011,33(5):99-102.[邹良志,谢然红.岩心刻度测井在建立测井解释模型中的应用[J].石油天然气学报,2011,33(5):99-102.]

[5] Wang Yongdong,Wang Yanlong.The establishment of porosity interpretation model by using method of binary line regression[J].Journal of Northwest University:Natural Science Edition,2010,(4):34.[王永东,王彦龙.利用二元回归法建立砂岩孔隙度解释模型[J].西北大学学报:自然科学版,2010,(4):34.]

[6] Hao Fang,Dong Weiliang,Zou Huayao,et al.Overpressure fluid flow and rapid accumulation of natural gas in Yinggehai Basin[J].Acta Petrolei Sinica,2003,24(6):79-85.[郝芳,董伟良,邹华耀,等.莺歌海盆地汇聚型超压流体流动及天然气晚期快速成藏[J].石油学报,2003,24(6):79-85.]

[7] Yong Shihe,Zhang Chaomo.Logging Data Processing and Integrated Interpretation[M].Beijing:Petroleum University Press,1996.[雍世和,张超谟.测井数据处理与综合解释[M].北京:石油大学出版社,1996.]

[8] Archie G E.The electrical resistivity log as an aid in determining some reservoir characteristics[J].American Institute of Mining Metallurgical Engineers,2013,146(4):54-62.

[9] Li Xia,Shi Yujiang,Wang Ling,et al.Logging identification and evaluation technique of tight sandstone gas reservoirs:Taking Sulige Gasfield as an example[J].Natural Gas Geoscience,2013,24(1):62-68.[李霞，石玉江,王玲,等.致密砂岩气层测井识别与评价技术——以苏里格气田为例[J].天然气地球科学,2013,24(1):62-68.]

[10] He Jiaxiong.To discuss the cause of CO2 formation in Yinggehai Basin and to reply professor Chen Jianyu[J].Natural Gas Geoscience,2003,14(5):412-415.[何家雄.再论莺歌海盆地 CO2 成因问题——兼答陈建渝教授[J].天然气地球科学,2003,14(5):412-415.]

[11] Du Jianguo.The cause of high concentration of carbon dioxide in natural gas,China[J].Natural Gas Geoscience,1991,2(5):203-208.[杜建国.中国天然气中高浓度二氧化碳的成因[J].天然气地球科学,1991,2(5):203-208.]

[12] Xiao Liang,Liu Xiaopeng,Miao Zhiqiang.A computaion method for reservoir permeability by combining NMR log and capillary pressure data[J].Acta Petrolei Sinica,2009,30(1):100-103.[肖亮,刘晓鹏,毛志强.结合NMR和毛管压力资料计算储层渗透率的方法[J].石油学报,2009,30(1):100-103.]

[13] Mao Zhiqiang,Zhang Chong,Xiao Liang.A new method based on nuclear magnetic resonance logging to calculate reservoir porosity in low porosity and low permeability gas reservoir[J].Oil Geophysical Prospecting,2010,45(1):105-109.[毛志强,张冲,肖亮.一种基于核磁共振测井计算低孔低渗气层孔隙度的新方法[J].石油地球物理勘探,2010,45(1):105-109.]

[14] Sima Liqiang,Wang Peichun,Deng Xianhai.Discussion of calculation methods to calculate reservoir porosity in Feixianguan Formation in northeastern Sichuan[J].Journal of Southwest Petroleum University:Science & Technology Edition,2008,30(2):1-4.[司马立强,王培春,邓先海.川东北飞仙关组储层孔隙度计算方法探讨[J].西南石油大学学报:自然科学版,2008,30(2):1-4.]

[15] Qi Lixin,Fan Zhengjun,Li Zongjie,et al.Establishment and application of three porosity log model in Tahe Oilfield[J].Geophysical Prospecting for Petroleum,2010,49(5):489-495.[漆立新,樊政军，李宗杰，等.塔河油田碳酸盐岩储层三孔隙度测井模型的建立及其应用[J].石油物探,2010,49(5):489-495.]

[16] Fan Mingtao,Shen Quanyi,Wu Hui,et al.The research of method to calculate porosity in fracture-pore reservoir with complex lithology[J].Natural Gas Industry,2005,25(5):29-34.[范铭涛,沈全意,吴辉,等.复杂岩性裂缝—孔隙型储层孔隙度计算方法研究[J].天然气工业,2005,25(5)：29-34.]

[17] Hung Xiaoping,Chai Jing.The application of Archie formula in calculating oil saturation in shale[J].Petroleum Geology and Recovery Efficiency,2014,21(4):58-62.[黄小平,柴婧.阿尔奇公式在泥页岩地层含油饱和度计算中的应用[J].油气地质与采收率,2014,21(4):58-62.]