页岩渗透率测试方法研究与应用

摘要
关键词
引言
1 页岩渗透率测试仪器和解释模型
1.1 渗透率测试仪器结构
1.2 仪器改进及测试气体选择
图1（Fig.1）
表1（Table 1）
图2（Fig.2）
1.3 测试步骤
1.4 考虑吸附的渗透率解释模型
2 吸附对渗透率测试值的影响
图3（Fig.3）
图4（Fig.4）
3 误差及测试结果分析
3.1 误差分析
图5（Fig.5）
3.2 测试结果分析
表2（Table 2）
表3（Table 3）
图6（Fig.6）
表4（Table 4）
4 结论
参考文献

引用本文

Cao Cheng,Li Tiantai,Wang Hui,et al.Research and application of shale permeability test method [J].Natural Gas Geoscience,2016,27(3):503-512.[曹成，李天太，王晖，等.页岩渗透率测试方法研究与应用[J].天然气地球科学，2016,27(3):503-512.]
doi:10.11764/j.issn.1672-1926.2016.03.0503

页岩渗透率测试方法研究与应用

曹成^1，2，李天太^1，3，王晖²，许小强²，高潮²

（1.中国石油大学（北京）石油工程学院，北京102249；2.陕西延长石油（集团）有限责任公司研究院，陕西西安710075；3.西安石油大学石油工程学院，陕西西安710065）

作者简介：曹成（1984-），男，陕西延安人，博士研究生，主要从事页岩气藏地质建模与数值模拟研究.E-mail：caochengyanlian@163.com.

基金项目：国家高技术研究发展计划（863计划）“页岩气钻完井及储存评价与产能预测技术研究”（编号：2013AA064501）；陕西省科技统筹创新工程计划“陆相页岩气资源地质研究与勘探开发关键技术攻关”（编号：2012KTZB03-01-01）联合资助.

摘要

为了减小页岩渗透率测试误差与缩减测试时间，针对目前页岩渗透率测试中存在的问题。改进传统脉冲衰减渗透率测试仪器为可变上下游储室体积；增加旁通管线；选用甲烷为页岩渗透率测试气体；并建立考虑吸附的页岩渗透率解释模型；在此基础上对鄂尔多斯盆地长7纯页岩、含砂质夹层页岩和砂质纹层岩心进行测试分析。结果表明:①氦气测试渗透率会高于甲烷测试渗透率，氮气测试渗透率低于甲烷测试渗透率，甲烷测试渗透率可以反映真实天然气渗流规律及页岩渗透率。②兰格缪尔体积和孔隙压力越大有效吸附孔隙度越小。③不考虑吸附会对页岩渗透率的测试造成低估；页岩吸附能力越强、孔隙压力越低、兰格缪尔压力越高时，渗透率低估值越大。④经验证，改进的渗透率测试仪器测试结果是真实可靠的，最多可减小7h总测试时间，并可降低孔隙体积误差所造成的渗透率测试误差。⑤测试流体方向不同会导致不同的渗透率测试结果；吸附对纯页岩渗透率测试低估值最高可达97%，必须进行吸附校正，但对砂质夹层渗透率测试低估值最高仅为7.5%，可以忽略其影响。

关键词：页岩渗透率脉冲衰减法有效吸附孔隙度测试误差兰格缪尔体积兰格缪尔压力

中图分类号:TE135 文献标志码:A 文章编号:1672-1926(2016)03-0503-10

Research and application of shale permeability test method

Cao Cheng^1，2，Li Tian-tai^1，3，Wang Hui²，Xu Xiao-qiang²，Gao Chao²

（1.College of Petroleum Engineering,China University of Petroleum,Beijing 102249,China;2.Research Institute of Shaanxi Yanchang Petroleum （Group）Co,Ltd.,Xi’an 710075,China;3.College of Petroleum Engineering,Xi’an Shiyou University,Xi’an 710065,China）

Abstract

On the basis of existing problems in the shale permeability test,in order to reduce the test errors and time,the upstream and downstream reservoir chambers of traditional pulse decay permeability apparatus are improved into variable volume chambers with a by-pass pipe.Proper test gases are selected to calculate the true permeability value,and the shale permeability interpretation model considering adsorption is established.Tests and analysis are conducted on pure shale,sand shale and intercalation sandy laminated cores of Ordos Basin Chang 7 section.Results show that: (1)Permeability measured with helium is higher than that measured with methane,and lower than that measured with nitrogen,and permeability measured with methane can reflect the real gas seepage rule and shale permeability.(2)The larger the Langmuir volume and the pore pressure,the smaller the effective adsorption porosity.(3)If adsorption is not considered,shale permeability will be underestimated; the extent of underestimation is much bigger with stronger adsorption ability,lower pore pressure and higher Langmuir pressure.(4)The test result obtained from the improved permeability apparatus is reliable,it can reduce up to 7 hours of the total test time,and can reduce system error caused by pore volume errors.(5)Different fluid directions can lead to different permeability test results; the extent of underestimation caused by adsorption is 97% for the pure shale,and must be corrected; for sand interlayer the extent of underestimated caused by adsorption is 7.5%,and can be ignored.

Key words： Shale; Permeability; Pulse decay method; Effective adsorption porosity; Test error; Langmuir volume; Langmuir pressure;

Show Figures

引言

近年来，页岩气作为常规油气类型的重要补充和接替，具有重要的战略地位。页岩气勘探开发正由北美向全球扩展^[1]，页岩气藏因其资源丰富、潜力巨大成为研究的热点^[2]。国外对页岩渗透率测试的研究相对成熟^[3-7]，国内多集中于页岩气的产能评价、数值模拟等方面的研究^[8-12]，对页岩渗透率的研究大多归于理论计算^[13-16]，而对页岩渗透率测试等方面研究少之又少。国内大多将常规岩心渗透率测试方法用于对页岩的测试^[17-19]，李智峰等^[20]首次引入原地测试法、改良脉冲衰减测试法和解吸流动法作为页岩渗透率测试方法，于荣泽等^[21]调研了岩心柱脉冲衰减法、岩屑脉冲衰减法、脱气法。以上这些方法在测试页岩渗透率时存在不足:①测试气体都为氦气或者氮气，但氦气和氮气与甲烷存在较大的区别，因此氦气和氮气所测页岩渗透率如果用于天然气渗流规律的分析会导致误差^[22]；②微纳米级别的页岩基质孔隙比表面很大，对气体有很强的吸附能力，吸附在孔隙表面的气体分子层会影响渗透率测试值，因此目前实验方法和条件下所测的渗透率大多是由吸附影响的表观渗透率，不能反映页岩的真实渗透率；③未考虑测试流体方向对页岩渗透率的影响；④传统的脉冲衰减渗透率上下游储室的体积大小不变，因此对于孔隙体积不同的岩心，误差在不可控制的范围内。基于以上原因，本文在已有脉冲衰减渗透率测试仪的基础上进行改进，并建立考虑吸附的渗透率解释模型；针对鄂尔多斯盆地延长组长7段纯页岩、含砂质夹层页岩和砂质纹层岩心进行测试分析。

1 页岩渗透率测试仪器和解释模型

1.1 渗透率测试仪器结构

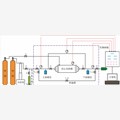
渗透率测试仪器包括7大部分，分别为注射泵、真空泵、手摇泵、压力发生器、恒温箱、控制箱及数据采集系统。岩心夹持器用304耐高压不锈钢材料制成，内部装有橡胶套和U型密封圈，可以增强密封性能；径压和围压通过岩心夹持器内置泵施加，岩心进口和出口处由端塞固定，侧向由活塞衬套固定，这样可以保证流体只沿轴向流动；气体进口和出口分别装有温度和压力传感器；压力脉冲通过压力发生器完成；实验装置配有恒温器，以保证注入气体保持在恒定的温度；甲烷气体通过注射泵进入到岩心中；数据采集系统记录实验过程中的覆压、温度，上下游储室压力（图1）。

1.2 仪器改进及测试气体选择

根据文献[7]可知，当上下游储室体积与岩心孔隙体积比值为0.25时，65%的孔隙体积误差所造成的渗透率测试误差小于2%，当比值为0.5时，25%的孔隙体积误差所造成的渗透率测试误差小于2%。可以看出，岩心孔隙体积与上下游储室体积比值越小，所造成的渗透率测试误差越小，但测试时间也会相应变长^[23]。因此，本文测试仪器的上下游储室体积大小根据所测岩心孔隙体积的大小来调整（图1），以达到降低岩心孔隙体积与上下游储室体积比值，减小因孔隙体积误差而导致渗透率测量误差的目的；推荐岩心孔隙体积与上下游储室体积比值为0.25~0.5，以保证在相对较短的测试时间内减少误差。在计算渗透率时，上游储室体积还应包括上游连接管线和压力监测仪中孔隙体积，上下游储室体积必须对称，以减小误差。阀门3和阀门8之间的旁通管线可以实现单次测试正反向渗透率，对于脉冲衰减渗透率测试方法，很大一部分时间都花费前期系统压力温度平衡的过程中，因此如果一块岩心在测试完正向渗透率后，还需继续测试反向渗透率时，则所有的过程都必须重复进行，在这个过程中系统压力和温度必须重新达到平衡，调试的过程不能保证实验条件与上次完全一致，因此存在一定的人为误差，使用旁通管线便可减小因岩心装卸和系统再次平衡而浪费的时间，而且还可以消除人为误差。

Figure Option
Download Create PPT

图1 页岩渗透率测试原理
Fig.1 The principle diagram of the shale permeability test

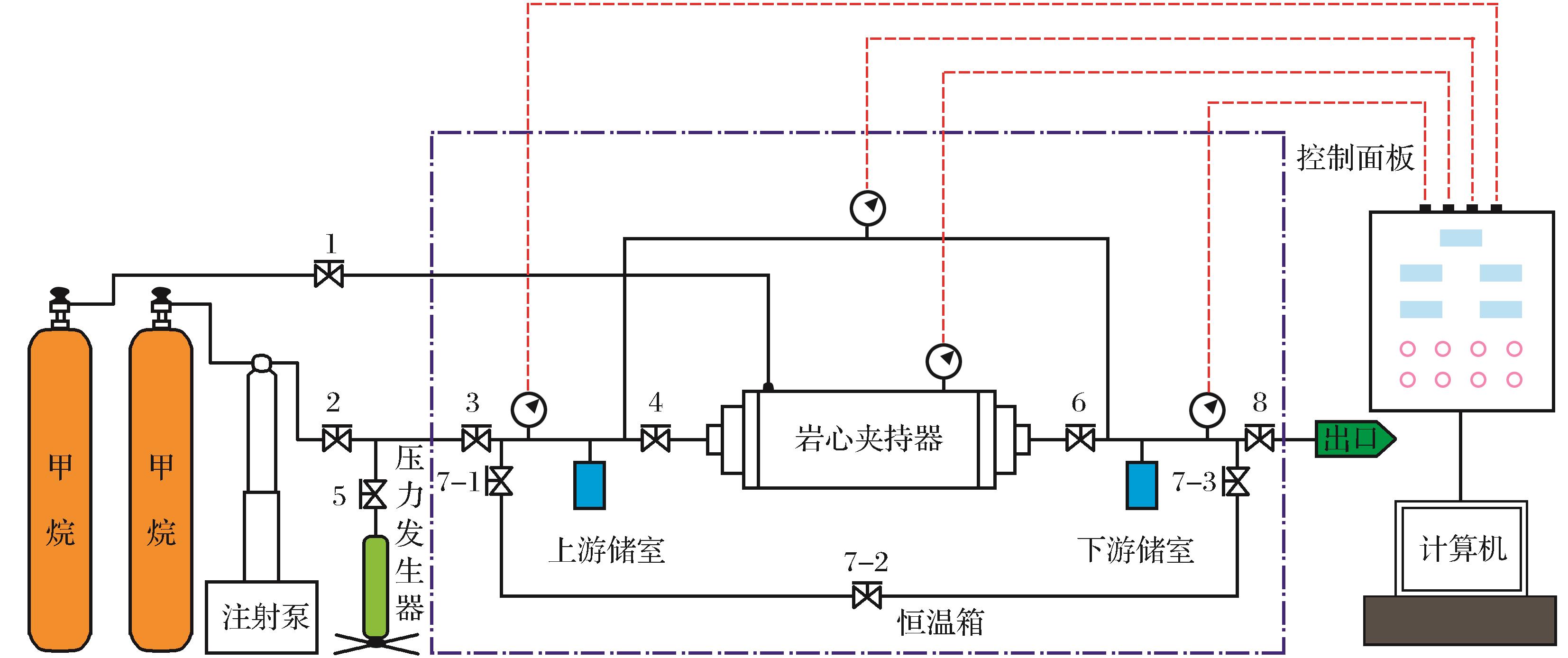
氦气、氮气和甲烷的气体性质见表1，其中σ_c、σ_k、σ_eff分别为气体碰撞直径、动力直径和有效气体直径，氦气的有效气体直径(0.259nm)与氮气的有效气体直径(0.366nm)都小于甲烷(0.381nm)，由于页岩基质孔径大多为微纳米级别，分子动力半径较小的氦气和氮气更容易通过基质孔隙，而甲烷的有效气体直径较大，会被部分极小的孔隙所阻挡；氦气属于惰性气体，其与页岩基质之间基本不发生化学反应；页岩吸附3种气体的能力不同，对氦气吸附量最少，对甲烷吸附量最大，吸附量越大，基质有效孔径越小，气体通过能力越低。基于以上原因，使用氦气或氮气所测试的页岩渗透率不能反映甲烷在页岩中的渗流规律。Shieh等^[24]分别用氦气、氮气和甲烷对同一样品测试气体渗透系数和扩散系数（图2），得到完全不同的结果；Cui等^[22]用氮气和甲烷测试同一样品渗透率，同样得到不同的渗透率值。可以看出，渗透率测试值对气体具有选择性，因此氦气和氮气测试渗透率不等同于甲烷测试渗透率，本文用天然气中主要组分甲烷作为测试气体。

表1 测试气体性质
Table 1 Properties of test gas

	σ_c/nm	σ_k/nm	σ_eff/nm	T_c/K
He	0.258	0.26	0.259	5.26
N₂	0.368	0.364	0.366	126.2
CH₄	0.382	0.38	0.381	190.7

Figure Option
Download Create PPT

图2 不同气体的气体渗透系数和扩散系数(据Shieh等^[24])
Fig.2 Gas permeability coefficient and diffusion coefficient of difference gas(according to Shieh et al^[24])

1.3 测试步骤

测试步骤:①将直径为38mm，长度为25mm的岩心装入岩心夹持器，围压设置为10.34MPa；②用实验气体冲洗实验装置；③将样品初始平衡压力设置为6.89MPa，关闭阀门4和阀门7-1—阀门7-3；④使用压力发生器将上游储室压力调为7.10MPa；⑤打开阀门4，记录上游储室和下游储室压力变化和时间直至压力达到平衡；⑥打开阀门7-1—阀门7-3，关闭阀门4和阀门6；⑦将下游压力设置为7.10MPa；⑧关闭阀门7-1—阀门7-3，打开阀门4和阀门6；记录下游和上游压力随时间变化数据。

1.4 考虑吸附的渗透率解释模型

气体在上游和下游压差的作用下通过岩心的过程可用质量守恒方程表示，吸附的影响以源项的形式加入到质量守恒方程中。

(ρ φ) + (1 - φ) \frac{q}{t} = (\frac{ρ k}{μ} \frac{p}{x})

(1)

其中：

ρ = \frac{Mp}{ZRT}

(2)

式(1)—式(2)中:ρ为气体密度，m³/kg；φ为页岩真实孔隙度，无因次；q为页岩单位体积的吸附量，kg/m³；k为页岩渗透率，×10^-3μm²；μ为气体黏度，mPa·s；p为孔隙压力，MPa；t为时间，s；M为气体摩尔质量，g/mol；Z为气体压缩因子，无因次；R为气体常数，8.314×10^-6MPa·m³·mol^-1·K^-1；T为绝对温度，K；x为岩心轴向方向。将式(2)带入式(1)，假设页岩孔隙不可压缩，则式(1)等号左边第一项化简为:

(\frac{Mp}{ZRT} φ) = \frac{M}{RT} φ (\frac{p}{Z})

(3)

其中：

(\frac{p}{Z}) = \frac{\frac{p}{t} \cdot Z - p \frac{Z}{t}}{Z^{2}} = \frac{p}{Z} (\frac{1}{p} - \frac{1}{Z} \frac{Z}{p}) \frac{p}{t}

(4)

气体压缩系数为:

c_{g} = \frac{1}{p} - \frac{1}{Z} \frac{Z}{p}

(5)

将式(3)—式(5)带入式(1)，使用链式法则

\frac{q}{t}

\frac{q}{ρ}

\frac{ρ}{t}

后整理得:

[φ + (1 - φ) \frac{q}{ρ}] \times (\frac{μ c_{g}}{k} \frac{p}{Z}) \frac{p}{t} = (\frac{p}{Z} \frac{p}{x})

(6)

式(6)中：c_g为气体压缩系数，MPa^-1；由于压缩因子、压缩系数和黏度是随着压力而变化的，式(6)为非线性方程，定义拟时间:

t_{a} = \int </mo>t_{0}\frac{(μ C_{t})_{i}}{μ (\bar{p}) C_{t} (\bar{p})}dt

(7)

将式(7)带入式(6)后，得到拟时间表示的质量守恒方程:

[φ + (1 - φ) \frac{q}{ρ}] \times [\frac{(μ c_{g})_{i}}{k} \frac{p}{Z}] \frac{p}{t_{a}} = (\frac{p}{Z} \frac{p}{x})

(8)

定义拟压力:

ψ (p) = 2 \int_{0}^{p} \frac{p}{μ z} dp

(9)

将式(9)带入式(8)，并令:

γ = \frac{k}{(μ c_{g})_{i} [φ + (1 - φ) \frac{q}{ρ}]}

(10)

得到拟时间和拟压力表示的线性化质量守恒方程:

\frac{ψ}{t_{a}} = γ \frac{</mo>2ψ}{x^{2}}

(11)

初始条件和边界条件: 当0

ψ_{(x, 0)} = ψ_{2 (0)}

(12)

当t>0时:

ψ_{(0, t)} = ψ_{1 (t)}

(13)

ψ_{(L, t)} = ψ_{2 (t)}

(14)

当x=0，t>0时:

\frac{d ψ_{1}}{dt} = \frac{k}{c_{g} μ L [φ + (1 - φ) \frac{q}{ρ}]} \frac{V_{p}}{V_{1}} \frac{ψ}{x}

(15)

当x=L，t>0时:

\frac{d ψ_{2}}{dt} = - \frac{k}{c_{g} μ L [φ + (1 - φ) \frac{q}{ρ}]} \frac{V_{p}}{V_{2}} \frac{ψ}{x}

(16)

式(12)—式(16)中：1，2表示上游和下游；L为岩心长度，mm；V_p为岩心孔隙体积，cm³，V₁为上游储室体积，cm³；V₂为下游储室体积，cm³；式(15)为岩心上游端部气体流入与流出的质量守恒方程；式(16)为岩心下游端部气体流入与流出的质量守恒方程。

2 吸附对渗透率测试值的影响

从式(10)可以看出，对于常规砂岩，吸附作用很小，q/ρ基本可以忽略不计，但对于吸附作用较强的页岩来说，q/ρ的影响是不容忽视的，如果忽略q/ρ，解释模型就变为常规砂岩的解释模型，所测的页岩渗透率为有效吸附渗透率，反映地是吸附层厚度影响的表观渗透率，而非真实的页岩渗透率，因此在确定页岩渗透率时必须考虑吸附的影响，从而得到真实的页岩渗透率。 q/ρ是影响页岩渗透率测试的重要参数，为此定义有效吸附孔隙度^[3]，讨论其变化规律。

φ_{a} = (1 - φ) \frac{q}{ρ}

(17)

式(17)中:页岩单位体积的吸附量q可用兰格缪尔等温吸附方程表示^[10]:

q = \frac{M ρ_{s} V_{m} p_{L} p}{V_{sdt} (p_{L} + p)}

(18)

式(18)中:ρ_s为页岩密度，kg/m³；V_std为标准状况下的摩尔体积，m³/mol；V_m为兰格缪尔体积，m³/t；p_L为兰格缪尔压力，MPa。式(17)中

\frac{q}{ρ}

可表示为:

\frac{q}{ρ} = \frac{q}{p} \times \frac{p}{ρ}

(19)

将式(18)带入式(19)中等号右边第一项得:

\frac{q}{p} = \frac{ρ_{s} V_{m} {Mp}_{L}}{V_{sdt}} \times \frac{p_{L}}{(p_{L} + p)^{2}}

(20)

对于式(19)中等号右边第二项，先求

\frac{ρ}{p}

，将式(2)带入

\frac{ρ}{p}

后得:

\frac{ρ}{p} = \frac{M}{RT} (\frac{p}{Z}) = \frac{M}{RT} \frac{Z - p \frac{Z}{p}}{Z^{2}} = \frac{M}{RT} \frac{p}{Z} (\frac{1}{P} - \frac{Z}{p}) = \frac{M}{RT} \frac{p}{Z} c_{g}

(21)

将式(19)—式(21)带入式(17)后得到考虑吸附的有效吸附孔隙度:

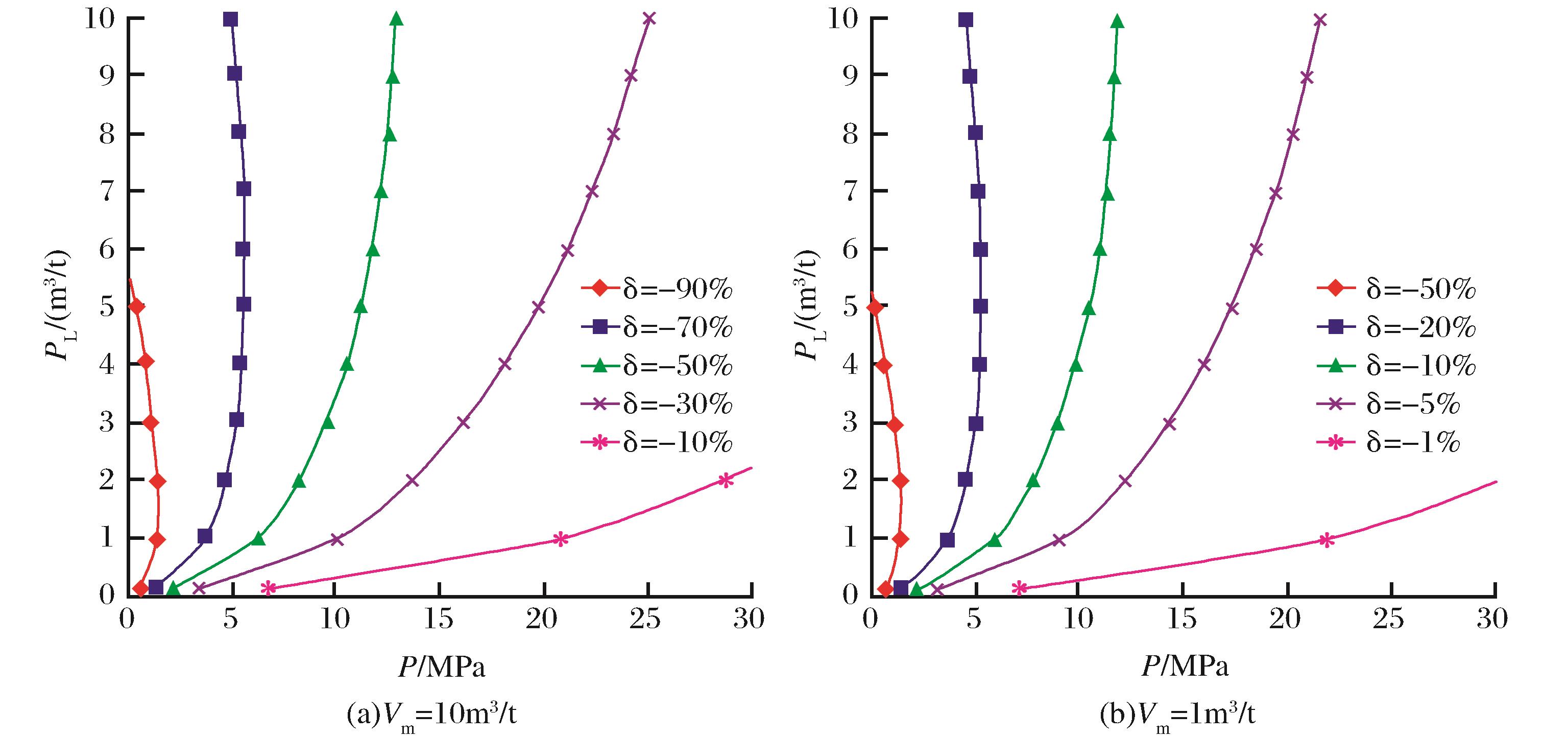
φ_{a} = \frac{ρ_{s} ZRT}{V_{std}} \frac{(1 - φ)}{c_{g}} \frac{V_{m} p_{L}^{2}}{p (p_{L} + p)^{2}}

(22)

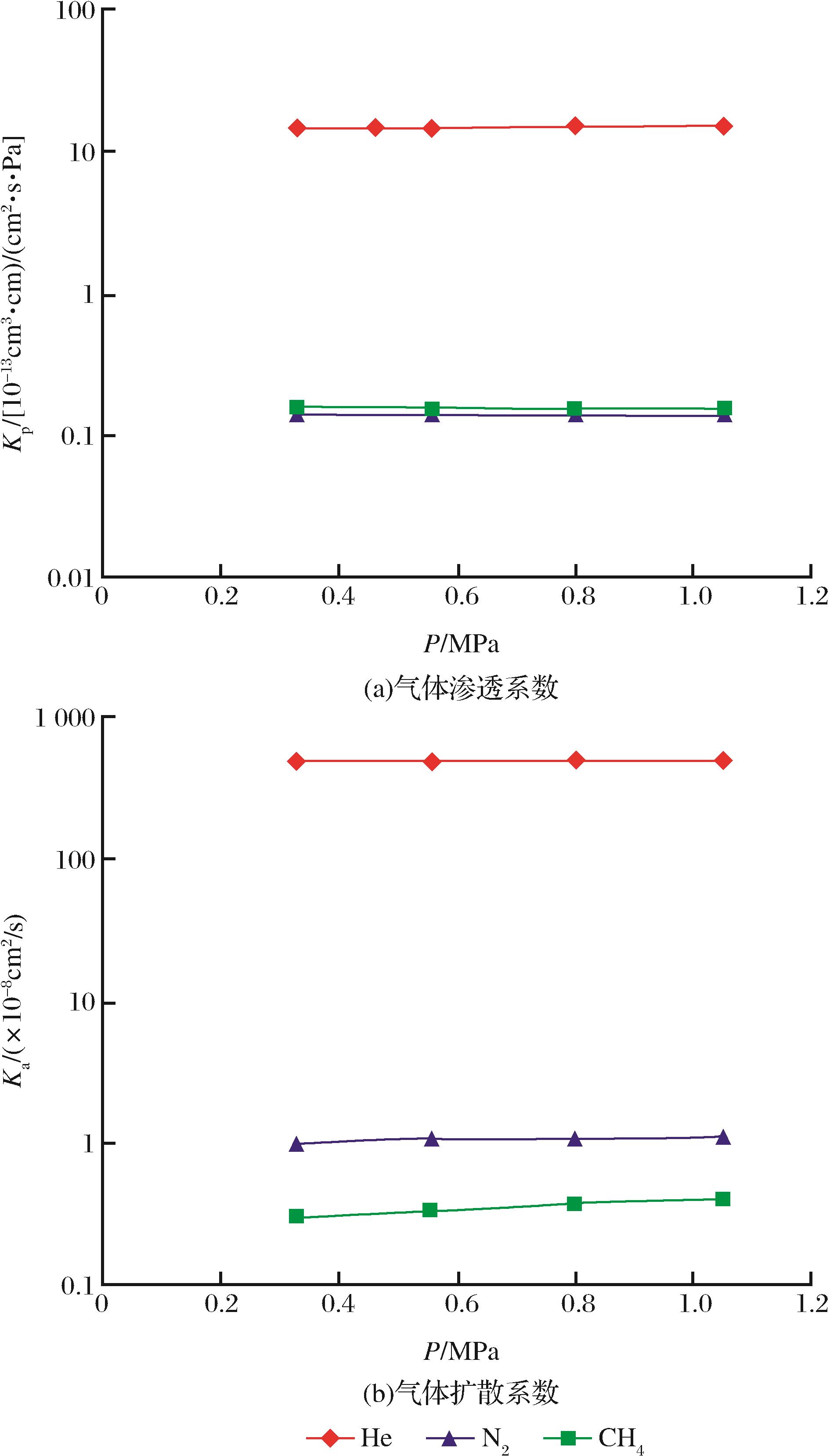
从式(22)可以看出，兰格缪尔体积、兰格缪尔压力和孔隙压力对有效吸附孔隙度的影响较大。兰格缪尔压力和兰格缪尔体积对有效吸附孔隙度的影响见图(3)；其中，Z取1；c_g为0.187Mpa^-1，μ_g为10.6×10^-3mPa·s；对于吸附能力较大的页岩，兰格缪尔体积为10m³/t时[图3(a)]，有效吸附孔隙度最高可达到80%；随着压力的升高，吸附孔隙度逐渐变小，在孔隙压力较高时，兰格缪尔压力越低，吸附孔隙度越小；当孔隙压力为10MPa，兰格缪尔压力为1MPa时，有效吸附孔隙度只有3%；当孔隙压力为3MPa时不同兰格缪尔压力下的有效孔吸附孔隙度可到达60%~80%；对于兰格缪尔压力为10MPa的有效吸附孔隙度曲线，随着压力的降低，有效吸附孔隙度上升速度小于兰格缪尔压力较低的有效吸附孔隙度上升速度。对于吸附能力较小的页岩，兰格缪尔体积为1m³/t[图3(b)]，最大有效吸附孔隙度可以达到8%；孔隙压力较低时，最小有效吸附孔隙度为1%。可以看出即使吸附能力很小的页岩，吸附影响有效吸附孔隙度，从而影响孔隙中气体的运移，对渗透率的测试造成误差。

Figure Option
Download Create PPT

图3 兰格缪尔压力和兰格缪尔体积对有效吸附孔隙度的影响
Fig.3 The effect of Langmuir pressure and Langmuir volume on effective adsorptive porosity

用Hsieh等^[6]和Dicker等^[23]解法对式(11)—式(16)求解，并表示为上游储室拟压力和下游储室拟压力之差:

Δ ψ = \frac{ψ_{u} (t_{ad}) - ψ_{d} (t_{ad})}{ψ_{u} (t_{0}) - ψ_{d} (t_{0})} = 2 \sum_{i}^{ SymboleB @} \frac{a (b^{2} + θ_{i}^{2}) - (- 1)^{i} b \sqrt{(a^{2} + θ_{i}^{2}) (b^{2} + θ_{i}^{2})}}{θ_{i}^{2} (θ_{i}^{2} + a + a^{2} + b + b^{2}) + ab (a + b + ab)} \times e_{ad}^{- θ_{i}} ad

(23)

其中θ_i、a和b构成超越方程:

\tan θ = \frac{(a + b) θ}{θ^{2} - ab}

(24)

式(24)中a和b分别为岩心孔隙体积与上下游储室体积之比:

a = \frac{V_{P}}{V_{1}}

(25)

b = \frac{V_{P}}{V_{2}}

(26)

V_{p} = A φ L

(27)

上式中，A为岩心横截面，mm²。

t_{ad} = \frac{kt}{μ c_{g} L^{2} φ (1 + β_{a})}

(28)

β_a为吸附影响因子:

β_{a} = (1 - φ) \frac{q}{ρ} / φ

(29)

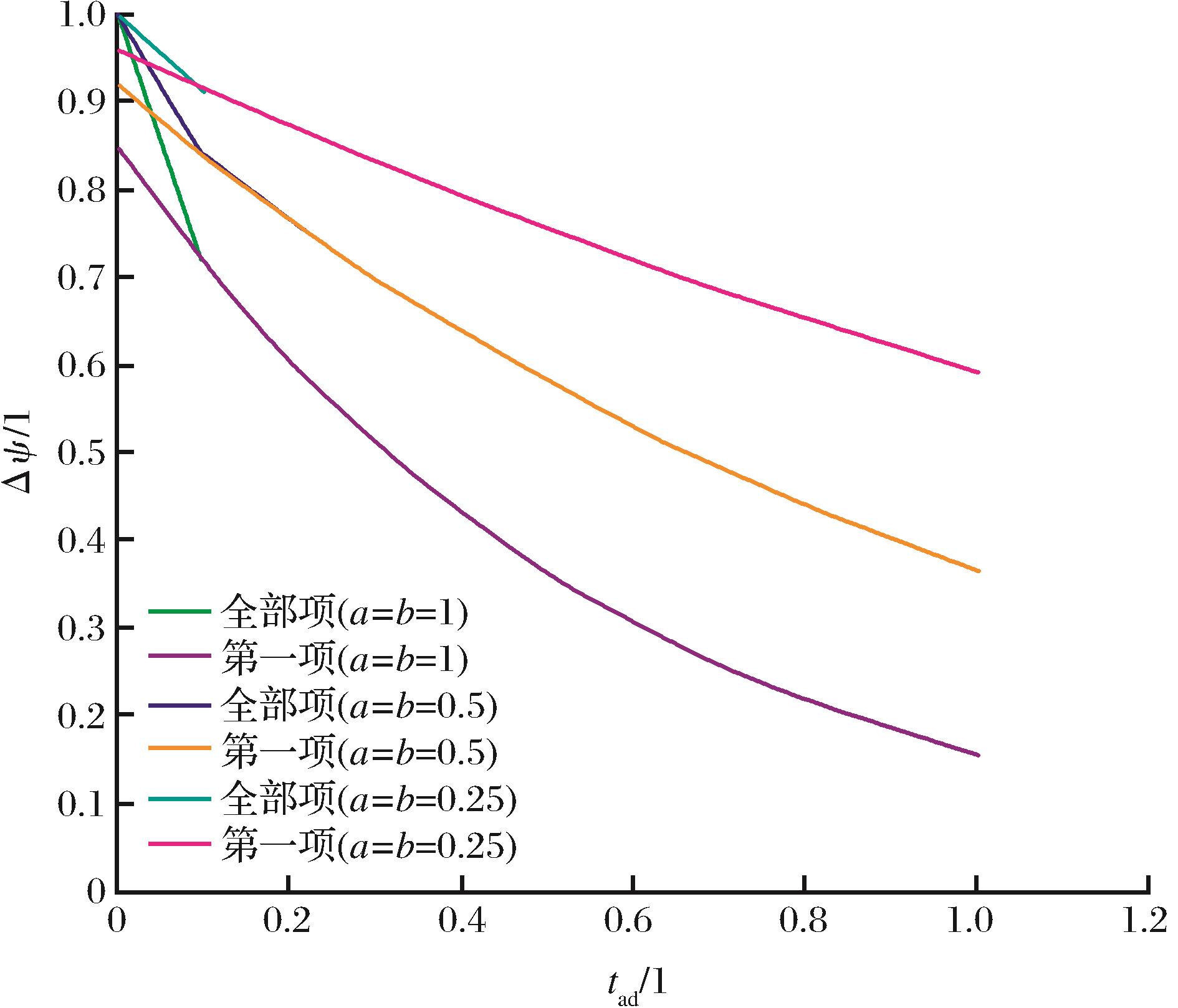
式(23)为无穷项指数函数的和，其中第一项所占的比例远大于剩余项，且当a和b相等时，偶数项为0，只剩余奇数项，从图4可以看出，对于t_ad=0.1，当a=b=1时，第一项所占比例为84.98%，当

Figure Option
Download Create PPT

图4 a和b值对拟压力数据的影响
Fig.4 The effect of a and b on the pressure

a=b=0.5时，第一项所占比例为92.09%，当a=b=0.25时，第一项所占比例为95.93%，可以看出a和b越小，忽略高阶项所造成的误差越小；且随着t_ad增大，a和b越小，越早变为单指数递减；因此在a和b相等情况下，如果使用单指数递减时间段的拟压力数据，忽略高阶奇数项后式(23)变为单指数函数，两边取对数得到:

Ln (Δ ψ) = Ln (f_{0}) + s_{1} t_{a}

(30)

其中:

f_{o} = 2 \frac{a (b^{2} + θ_{i}^{2}) - (- 1)^{i} b \sqrt{(a^{2} + θ_{i}^{2}) (b^{2} + θ_{i}^{2})}}{θ_{i}^{2} (θ_{i}^{2} + a + a^{2} + b + b^{2}) + ab (a + b + ab)}

(31)

s_{1} = \frac{θ_{1}^{2} k}{μ c_{g} L^{2} φ (1 + β_{a})}

(32)

考虑到式(27)和式(28)，并定义^[7]:

f_{1} = \frac{θ_{1}^{2}}{a + b}

(33)

得到页岩渗透率的计算式:

k = \frac{s μ_{g} c_{g} L (1 + β_{a})}{f_{1} A (\frac{1}{V_{u}} + \frac{1}{V_{d}})}

(34)

从式(34)中可以看出，如果不考虑吸附影响因子β_a，所测渗透率值则会偏小，为了研究吸附影响因子对测试结果的影响，定义渗透率偏差系数:

ε = \frac{k_{no - adp} - k_{adp}}{k_{no - adp}}

(35)

式(35)中:k_no-adp为不考虑吸附所测渗透率值;k_adp为考虑吸附所测渗透率值。吸附对渗透率的影响如图5，其中真实孔隙度取5%。对于吸附能力较强的页岩，兰格缪尔体积为10m³/t时，在压力为0~30MPa，兰格缪尔压力为0~10MPa范围内，不考虑吸附可造成的最大渗透率偏差达90%；随着压力增大，兰格缪尔压力减小，所造成的渗透率偏差越小，在压力为7~30MPa，兰格缪尔压力为0~2MPa，所造成的渗透率偏差小于10%。对于吸附能力较弱的页岩，在同样的范围内，所造成的最大偏差为50%；在压力为7~30MPa，兰格缪尔压力为0~2MPa之间，所造成的渗透率偏差小于1%。由此可以看出，即使对于吸附能力较弱的页岩，在测试范围为10MPa左右时，不考虑吸附所造成的渗透率测试偏差也是不容忽视的。

3 误差及测试结果分析

3.1 误差分析

在对式(23)到式(30)的近似简化过程中，存在一定的误差，近似简化引起渗透率计算误差的影响较小(小于5%)。同时系统本身会存在一定的误差，如泄漏误差、温度波动误差、结构不对称产生的误差、除气不净导致误差、岩心表面薄膜引起误差及计量误差（表2）。以有限元渗流模型模拟脉冲衰减渗透率的误差标准^[25]评定本文实验装置的误差。本文实验装置泄漏率为10^-15m³/Pa，温度波动小于3%，对称性1.05，岩心气泡含量0.1mL，薄膜厚度较小，游标卡尺精度0.1mm，压差计精度0.5%，总系统误差小于10%，对于低渗透页岩岩心来说，在可以接受的误差范围内。在计算渗透率时要确定式(34)中的参数f₁，f₁ 的确定要用到岩心孔隙体积，但对岩心体积的估计

Figure Option
Download Create PPT

图5 吸附引起的渗透率测试误差
Fig.5 The errors of testing permeability by adsorption

往往存在一些人为的误差。对于PoroPDP-200渗透率测试仪，上下游储室体积一般固定为5cm³，但对于不同孔隙体积的岩心，岩心孔隙体积与上下游储室体积之比(a和b)的变化比较大，当孔隙体积比较大时，a和b会变大，这时如果给定的孔隙体积误差较大时，渗透率的误差较大。但如果使用可变上下游储室体积，使二者比值在0.25~0.5的范围内，可缩小孔隙体积误差引起的渗透率计算误差。从表3可以看出，对于研究区的一块纯页岩，如果使用固定(5cm³)上下游储室体积V₁，则50%的孔隙体积误差可引起4.47%的渗透率误差，但如果将V₁变为10cm³，50%的孔隙体积误差所引起的渗透率误差降低将近一倍(2.79%)。

3.2 测试结果分析

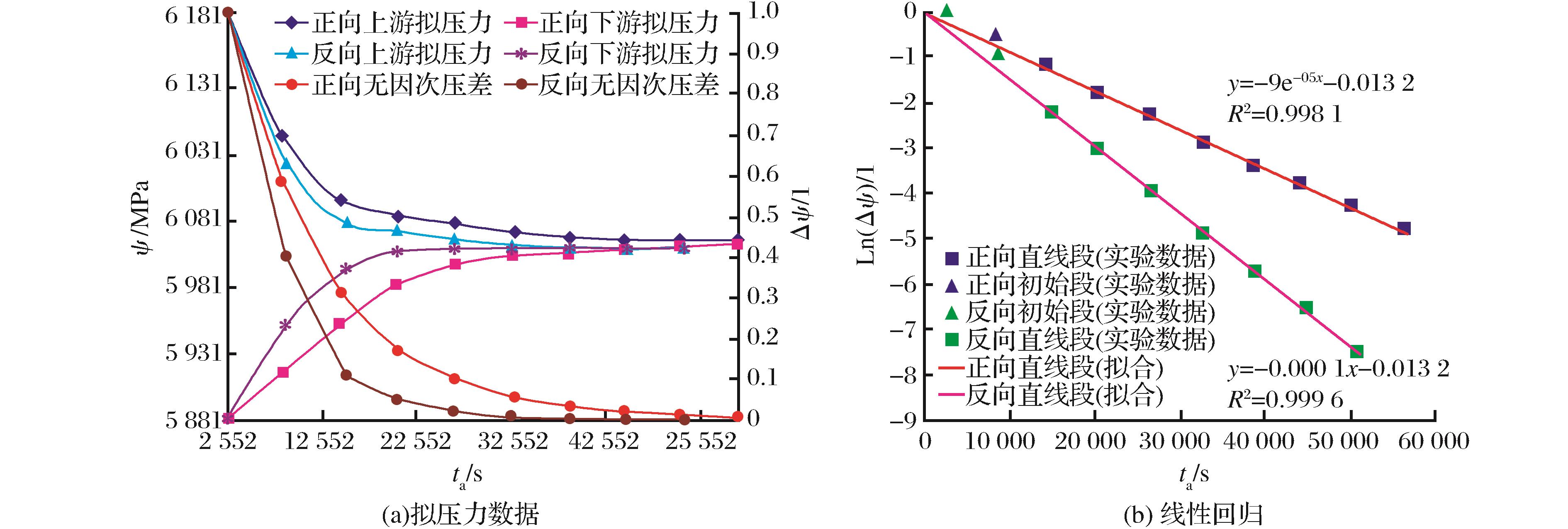
本文测试所用岩心为鄂尔多斯盆地延长组长7段纯页岩、含砂质纹层页岩、砂质夹层岩心，共计10块岩心；分别采用常规脉冲衰减渗透率测试仪(美国岩心公司的PoroPDP-200渗透率测试仪)和本文测试仪器测试相同的页岩，用式(7)和式(9)将压力数据和时间数据转化为拟压力和拟时间数据后进行渗透率计算；其中:压缩系数为0.187×10^-6Pa，动力黏度为10.6×10^-6Pa·s。图5为第一块岩心的计算结果，正向渗透率测试无因次拟压力差数据和反向渗透率无因次拟压力差都从第三个数据点开始变为单指数递减[图6(a)]，因此在无因次拟压力半对数图版上都从第三个数据点往后进行线性回归[图6(b)]。

表2 误差分析
Table 2 Error analysis

误差源	误差原因	误差标准	本文实验误差
泄漏	实验系统各部件连接处的泄漏引起的误差	泄漏率为10^-10m³/Pa时,误差为8%	泄漏率为10^-15m³/Pa,误差为0.8%
温度波动	温度波动引起误差	温度波动小于5%,误差忽略	温度波动小于3%,误差忽略
结构对称性	上下游结构不对称引起的误差	对称性为1.3时,误差为10%	对称性1.05,误差2%
除气不净	残留气泡对测量结果产生的误差,	岩心气泡含量0.5mL时,误差为10%	岩心气泡含量0.1mL,误差为1%
岩心表面薄膜	岩心在加工时形成表面薄膜产生误差	薄面厚0.075mm时,误差10%	薄膜厚度较小,误差小于1%
计量误差	岩心尺寸计量、压差计量精度引起误差	/	游标卡尺精度0.1mm,误差0.1% 压差计精度0.5%,误差2%

表3 可变上下游体积对渗透率测试结果的影响
Table 3 The effect of changeable cell reservoir on the testing permeability

	V_p/cm³	V₁/cm³	a	f₁	k/(×10^-9μm²)	渗透率误差/%
标准V_p	3.04	5	0.608	0.90	1.79	1.79
50%误差后Vp	4.57	5	0.914	0.86	1.87	4.469 3
标准V_p	3.04	10	0.304	0.95	1.79	1.79
50%误差后V_p	4.57	10	0.457	0.92	1.84	2.793 3

Figure Option
Download Create PPT

图6 第一块岩心正向和反向拟压力和拟时间计算结果
Fig.6 The pseudo pressure calculation result of the first core in forward and reverse

PoroPDP-200渗透率测试仪和改进渗透率测试仪对同一块岩心测试正反渗透率，2种仪器的实验压力温度和测试气体均相同；在未考虑吸附的情况下，2种仪器测试的正反向渗透率结果很相近（表4第4、第5列和第7、第8列），说明本文所采用的渗透率仪器是真实有效的。同样可以看出，同一块岩心的正向渗透率和反向渗透率存在一定的差别，如果不考虑渗透率的方向，势必会造成错误的认识。从2种仪器的测试时间来看，第一块岩心测试时间最长为28h（表4第7列），但常规的渗透率测试仪所用时长为35h，改进后的仪器测试时间明显缩短。不同岩性的岩心吸附能力不相同，纯页岩的吸附能力较大，含砂质纹层页岩次之，砂岩夹层最小，如果不考虑吸附，则纯页岩造成的渗透率低估误差最大，最高可以达到97%，而砂质夹层的吸附性能较弱，渗透率低估值最高只有7.5%，因此对于砂岩夹层，

表4 渗透率测试结果
Table 4 The result of testing permeability

样号

岩性

孔隙度 /%

PoroPD-200 (未考虑吸附)

本文仪器(未考虑吸附)

本文仪器(考虑吸附)

总测试时间 /h

吸附误差 /%

正向渗透率 (×10^-3μm²)

反向渗透率 (×10^-3μm²)

总测试时间 /h

正向渗透率 (×10^-3μm²)

反向渗透率 (×10^-3μm²)

正向渗透率 (×10^-3μm²)

反向渗透率 (×10^-3μm²)

纯页岩

2.69

1.80×10^-6

1.87×10^-6

35.13

1.79×10^-6

1.99×10^-6

3.10×10^-6

3.44×10^-6

28.395

-73.07

纯页岩

2.22

5.80×10^-5

6.50×10^-6

17.65

6.20×10^-6

7.00×10^-6

1.22×10^-5

1.38×10^-5

13.88

-97.27

纯页岩

3.54

9.10×10^-5

9.00×10^-6

3.3

8.90×10^-6

8.50×10^-6

1.54×10^-5

1.47×10^-5

1.6

-72.60

含砂质纹层页岩

3.36

9.36×10^-4

9.01×10^-4

4.85

9.37×10^-4

9.05×10^-4

1.57×10^-3

1.52×10^-3

2.79

-68.06

含砂质纹层页岩

3.50

4.91×10^-4

1.80×10^-3

5.56

4.90×10^-4

1.50×10^-3

7.65×10^-4

2.34×10^-3

4.26

-56.07

含砂质纹层页岩

3.74

1.33×10^-4

2.90×10^-4

6.13

1.28×10^-4

3.12×10^-4

1.73×10^-4

4.23×10^-4

4.14

-35.46

含砂质纹层页岩

3.96

6.03×10^-4

6.70×10^-4

4.96

6.01×10^-4

6.30×10^-4

9.51×10^-4

9.97×10^-4

3.92

-58.18

含砂质纹层页岩

4.14

5.78×10^-4

7.30×10^-4

5.58

6.32×10^-4

7.86×10^-4

9.30×10^-4

1.16×10^-3

3.81

-47.08

含砂质纹层页岩

5.48

2.55×10^-4

1.52×10^-4

3.68

2.52×10^-4

1.59×10^-4

3.12×10^-4

1.97×10^-4

2.93

-23.77

砂岩夹层

7.09

9.23×10^-4

8.49×10^-4

3.31

9.28×10^-4

8.58×10^-4

9.97×10^-4

9.22×10^-4

1.64

-7.47

砂岩夹层

7.14

3.58×10^-3

5.01×10^-3

2.51

3.59×10^-3

4.59×10^-3

3.79×10^-3

4.85×10^-3

1.74

-5.63

在误差允许的范围内可以忽略吸附的影响。

4 结论

(1)甲烷作为测试气体，可以得到准确的页岩渗透率测试值，该值可反映页岩中的气体渗流规律，可变上下游储室体积可以减小由孔隙体积误差而造成的渗透率测试误差。 (2)兰格缪尔体积、兰格缪尔压力和孔隙压力是影响有效吸附孔隙度的重要参数；孔隙度为5%，兰格缪尔体积为10m³/t时，有效吸附孔隙度最高可达到80%；兰格缪尔体积为1m³/t，最大有效吸附孔隙度可以达到8%；孔隙压力越大，有效吸附孔隙度越小；随着孔隙压力的降低，兰格缪尔压力越大，其对有效吸附孔隙度的影响越小。 (3)不考虑吸附的影响，会对页岩渗透率的测试造成低估；孔隙度为5%，兰格缪尔体积为10m³/t时，在压力为0~30MPa，兰格缪尔压力为0~10MPa范围内，不考虑吸附可造成的最大渗透率低估达90%；相同条件和范围内，兰格缪尔体积变为1m³/t时，所造成的最大低估为50%。 (4)测试流体方向对渗透率测试结果存在影响，渗透率值不可只用单一方向流体测试结果唯一表征；改进的页岩渗透率测试仪器最大可缩短7h的总测试时间。 (5)吸附对鄂尔多斯盆地纯页渗透率测试低估值最大为97%，必须进行吸附校正；对砂质夹层渗透率测试低估值最大为7.5%,在误差允许的范围内可以忽略吸附的影响。

参考文献(References)

[1] Xu Yongjian,Wu Aijun.The development status of shale gas in the world and its exploration prospect in China[J].Special Oil & Gas Reservoirs,2010,17(5):1-7,128.[徐建永,武爱俊.页岩气发展现状及勘探前景[J].特种油气藏,2010,17(5):1-7,128.]

[2] Zhang Jingchuan,Jin Zhijun,Yuan Mingsheng.Reservoiring mecahnism of shale gas and its distribution[J].天然气工业,2004,24(7):15-18,131-132.[张金川,金之钧,袁明生.页岩气成藏机理和分布[J].Natural Gas Industry,2004,24(7):15-18,131-132.]

[3] Cui X,Bustin A M M,Bustin R M.Measurements of gas permeability and diffusivity of tight reservoir rocks:different approaches and their applications[J].Geofluids,2009,9(3):208-223.

[4] Cheng Cao,Tiantai Li,Juntai Shi,et al.A new approach for measuring the permeability of shale featuring adsorption and ultra-low permeability[J].Journal of Natural Gas Science and Engineering，2016，30（2）：548-556.

[5] Chen T,Stagg P.Semilog analysis of the pulse-decay technique of permeability measurement[J].Society of Petroleum Engineers Journal,1984,24(6):639-642.

[6] Hsieh P A,Tracy J V,Neuzil C E,et al.A transient laboratory method for determining the hydraulic properties of ‘tight’rocks:I.Theory[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts Elsevier,1981,8(3):245-252.

[7] Jones S C.A technique for faster pulse-decay permeability measurements in tight rocks[J].SPE 28450,1997:19-26.

[8] Gao Shusheng,Yu Xinhe,Liu Huaxun.Impact of slippage effect on shale gas well productivity[J].Natural Gas Industry,2011,31(4):55-58,127.[高树生,于兴河,刘华勋.滑脱效应对页岩气井产能影响的分析[J].天然气工业,2011,31(4):55-58,127.]

[9] Cao Cheng,Li Tiantai,Zhang Lei,et al.Shale gas dual porosity-dual permeability model with matrix shrinking[J].Natural Gas Geoscience,2015,26(12):2282-2288.[曹成,李天太,张磊,等.考虑基质收缩效应的页岩气双孔双渗模型[J].天然气地球科学,2015,26(12): 2282-2288.]

[10] Yao Jun,Sun Hai,Fan Dongyan,et al.Transport mechanisms and numerical simulation of shale gas reservoirs[J].Journal of China University of Petroleum:Edition of Natural Science,2013,37(1):91-98.[姚军,孙海,樊冬艳,等.页岩气藏运移机制及数值模拟[J].中国石油大学学报:自然科学版,2013,37(1):91-98.]

[11] Xu Bingxiang,Li Xiangfang,Yin Bangtang.Influence of gas slippage on gas well productivity evaluation[J].Natural Gas Industry,2010,30(10):45-48,119.[徐兵祥,李相方,尹邦堂.滑脱效应对气井产能评价的影响[J].天然气工业,2010,30(10):45-48,119.]

[12] Cao Cheng,Li Tiantai,Liu Gang,et al. Permeability calculation model of shale matrix with the effect of adsorption,slippage and free molecule flow[J].Journal of Xi’an Shiyou University:Natural Science Edition,2015,30(5):48-53.[曹成,李天太,刘刚,等.考虑吸附、滑脱和自由分子流动效应的页岩基质渗透率计算模型[J].西安石油大学学报:自然科学版,2015,30(5):48-53.]

[13] Yu Rongze,Bian Yanan,Qi Yadong,et al.A review of numerical simulation of shale gas reservoirs[J].Oil Gas & Geology,2014,35(1):131-137.[于荣泽,卞亚南,齐亚东,等.页岩气藏数值模拟研究现状[J].石油与天然气地质,2014,35(1):131-137.]

[14] Li Zhiping,Li Zhifeng.Dynamic characteristics of shale gas flow in nanoscale pores[J].Natural Gas Industry,2012,32(4):50-53,123.[李治平,李智锋.页岩气纳米级孔隙渗流动态特征[J].天然气工业,2012,32(4):50-53,123.]

[15] Wang Rui,Zhang Ningsheng,Liu Xiaojuan,et al.Apparent permeability of shale considering the adsorption and diffusion of gas and the effects of temperature and pressure on it[J].Journal of Xi’an Shiyou University：Natural Science Edition,2013,28(2):3,49-53,83.[王瑞,张宁生,刘晓娟,等.考虑吸附和扩散的页岩视渗透率及其与温度—压力之关系[J].西安石油大学学报:自然科学版,2013,28(2):3,49-53,83.]

[16] Wang Rui,Zhang Ningsheng,Liu Xiaojuan,et al.The calculation and analysis of diffusion coefficient and apparent permeability of shale gas[J].Journal of Northwest University:Natural Science Edition,2013,43(1):75-80,88.[王瑞,张宁生,刘晓娟,等.页岩气扩散系数和视渗透率的计算与分析[J].西北大学学报:自然科学版,2013,43(1):75-80,88.]

[17] Gao Cheng,Xu Ruina,Xue Huaqing,et al.The application study based on the permeability measurement models of tight cores[J].Journal of Engineering Thermophysics,2013,34(9):1695-1698.[高诚,胥蕊娜,薛华庆,等.基于致密岩心的渗透率测试模型的应用研究[J].工程热物理学报,2013,34(9):1695-1698.]

[18] Zhang Hongxue,Liu Weiqun,Zhu Li.Fracture permeability model and experiments of shale gas reservoirs[J].Rock and Soil Mechanics,2015,36(3):719-729.[张宏学,刘卫群,朱立.页岩储层裂隙渗透率模型和试验研究[J].岩土力学,2015,36(3):719-729.]

[19] Zhang Kaihong,Chen Yijian,Xu Haiyin.A pressure pulse technique to test liquid permeability of core with low permeability.[J].Petroleum Instrument,1998,12(3):12-14,52.[张开洪,陈一健,徐海莹.测试低渗岩心液体渗透率的压力脉冲技术[J].石油仪器,1998,12(3):12-14,52.]

[20] Li Zhifeng,Li Zhiping,Wang Yang,et al.Comparison and analysis of permeability testing methods on shale gas reservoir[J].Fault-Block Oil & Gas Field,2011,18(6):761-764.[李智锋,李治平,王杨,等.页岩气储层渗透性测试方法对比分析[J].断块油气田,2011,18(6):761-764.]

[21] Yu Rongze,Bian Yanan,Zhang Xiaowei,et al.The review of non-steady permeability test in shale gas reservoir[J].Science Technology and Engineering,2012,12(27):7019-7027,7035.[于荣泽,卞亚南,张晓伟,等.页岩储层非稳态渗透率测试方法综述[J].科学技术与工程,2012,12(27):7019-7027,7035.]

[22] Cui X,Bustin R M,Dipple G.Selective transport of CO₂,CH₄,and N₂ in coals:Insights from modeling of experimental gas adsorption data[J].Fuel,2004,83(3):293-303.

[23] Dicker A,Smits R M.A practical approach for determining permeability from laboratory pressure-pulse decay measurements[C].SPE-17578,1988:285-292.

[24] Shieh J J,Chung T S.Gas permeability,diffusivity,and solubility of poly (4-vinylpyridine)film[J].Journal of Polymer Science Part B Polymer Physics,1999,37(20):2851-2861.

[25] Wang Ying,Li Xiaochun,Wei Ning.Error Analysis of storage-variable transient pulse method for permeability measurement[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(1):2746-2754.[王颖,李小春,魏宁.变容压力脉冲法渗透系数测量的误差分析[J].岩石力学与工程学报,2010,29(1):2746-2754.]